Алгоритмы алгебра: Памятки, подсказки, алгоритмы по математике 7-8 кл.

Алгоритмы по алгебре для 7 класса

Алгоритм записи одночлена в стандартном виде

1. Вычислить произведение числовых множителей (коэффициентов) одночлена и запись его на первом месте.

2. Определить какие переменные входят в одночлен, и записать их в алфавитном порядке.

3. Найти и записать степени переменных.

Алгоритм записи одночлена в стандартном виде

1. Записать все члены многочлена в стандартном виде.

2. Привести подобные слагаемые.

3. Определить степень каждого одночлена и записать их в алгебраическую сумму в порядке убывания степеней.

Алгоритм возведения двучлена в n-ю степень

1. Выписать в установленном порядке все одночлены которым подобны члены итогового многочлена.

2. Записать треугольник Паскаля для (n+1)-й строки.

3. Записать последовательно в качестве коэффициентов выписанных одночленов числа из (n+1)-й строки треугольника Паскаля.

4. При возведении в степень суммы (а+в)ⁿ поставить перед всеми одночленами знак «плюс».

5. При возведении в степень разности (а-в)ⁿ поставить перед первым одночленом знак «плюс», перед вторым одночленом — знак «минус» и далее чередовать знаки до последнего одночлена.

Алгоритм построения графика функции у=кх

1. Отметить на координатной плоскости Оху точку О с координатами (0;0).

2. Выбрать некоторое значение х₁=0.

3. Вычислить значение у₁=кх₁.

4. Отметить на координатной плоскости Оху точку А с координатами (х₁;у₁).

5. Через точки О и А провести прямую.

1. Выбрать два различных значения х: х₁ и х_{2 .}

2. Вычислить значение у₁=кх₁ +в_.

3. Вычислить значение у₂=кх₂+в.

4. Отметить на координатной плоскости Оху точку А с координатами (х₁;у₁).

5. Отметить на координатной плоскости Оху точку В с координатами (х₂;у₂).

6. Через точки А и В провести прямую.

Алгоритм решения линейного уравнения с одним неизвестным

Алгоритм решения линейного уравнения /кх+в/=с, к‡0

Алгебра и алгоритмы

Алгебра и алгоритмы

Home

Teaching

Courses

Алгалг

Аннотация

Основная цель курса: показать взаимное влияние алгебры и computer science, по дороге напомнив/познакомив слушателей с важными понятиями теории сложности вычислений. n}{n}\). [Wegener, §4.1, §4.2] [Верещагин—Шень, §1.3, Задача 13]

Алгоритмы в математике

Современные формы обучения, инновации в преподавании, введение новых
технологий диктуют учителю необходимость постигать секреты мастерства, а значит,
и совершенствовать методы обучения и воспитания учащихся.

Исследования психологов и педагогов, опыт коллег показывают: чтобы научить
детей самостоятельно учиться и проявлять творчество необходимо применение
деятельностного подхода в обучении. Для этого учащихся нужно замотивировать и
обучить их приемам и способам учебной деятельности, которые помогут сформировать
необходимые знания, умения и навыки.

Курс школьной математики имеет достаточно широкие возможности для применения
различных приемов, методов и технологий. В последние годы в содержание школьного
курса естественным образом закладывается алгоритмическая линия. Так как
применение алгоритмов является приоритетным в моей работе, то нужно отметить
что, между понятиями “прием” и “алгоритм” существует много общего, ни и есть
принципиальные отличия, а именно:

– прием – это рациональный способ работы, который состоит из отдельных
действий, он может быть выражен в виде правил или инструкций, его можно
перестроить и на его основе создать новый прием. Приемы деятельности допускают
самостоятельный выбор учениками конкретных действий по решению учебных задач;

– алгоритм – это общепонятное и однозначное предписание, которое определяет
последовательность действий, позволяющее достичь искомый результат. Алгоритм
предполагает жесткое выполнение шагов, а прием дает общее направление
деятельности по решению учебных задач, не регламентируя каждый шаг. Поэтому я в
своей работе выделяю два подхода: 1) обучение алгоритмам; 2) формирование
приемов решения задач. Школьные задачи делятся на: алгоритмические,
полуалгоритмические, полуэвристические и эвристические. Каждый тип задачи
предполагает свои схемы решения, подходы, применение логики и изобретательности.

На начальном этапе обучения математике применение алгоритмов способствует
формированию и прочному усвоению навыков владения математическими методами.
Также осуществляется подготовка к формированию первоначальных представлений о
математическом моделировании. Уже в начальных классах прослеживается применение
простейших алгоритмов выполнения арифметических операций, дети овладевают
навыками выполнения последовательных действий. Решают задачи с составлением схем
и кратких записей. Это можно рассматривать как пропедевтику операционного стиля
мышления.

Следующий уровень алгоритмической культуры учащихся – введение понятия
алгоритма и формирование его основных свойств. Это происходит в среднем звене
школы. Именно в этот период необходимо сочетания алгоритма и образца ответа, что
дает возможность ученику, верно, ответить на поставленный вопрос, сопроводив его
правильной речью. У учителя появляется возможность предлагать задачи с
элементами творчества. А материал, предлагаемый в наших школьных учебниках,
является хорошей базой для обучения составлению простейших алгоритмов и
дальнейшей их записи в разных формах. Мы применяем табличную, графическую
(блок-схема), словесную и формульную форму записи алгоритмов.

В качестве примера, иллюстрирующего процесс алгоритмизации как средство
обучения, можно указать на решение задач методом уравнений. Примером
графического алгоритма является блок-схема для отыскания количества решений
системы двух линейных уравнений с двумя неизвестными (см. Рисунок 1).

Отыскания числа решений системы двух линейных уравнений (блок-схема)

Рис. 1

Графические алгоритмы

Табличную форму алгоритма можно продемонстрировать на примере таблицы,
составляемой для исследования функций и дальнейшего построения графиков (см.
рис. 2).

Исследование функции и построение графика

Функция задана уравнением у = f(x). Исследовать
функцию и построить ее график.

1. Таблица исследования функции

2. Построение графика

Рис. 2

Табличный алгоритм

Пример формульного способа – последовательность нахождения компонентов при
составлении уравнения касательной к графику той или иной функции (см. рис. 3).

Уравнение касательной к графику функции

Рис. 3

Формульный способ

Словесный алгоритм используется практически во всех правилах выполнения
действий, например, правило сложения чисел с разными знаками (см. рис. 4).

Алгоритм сложения чисел с разными знаками

Рис. 4

Словесный алгоритм

В старших классах работа становится разнообразней и содержательней,
появляется возможность включать упражнения разного типа и уровня сложности,
предполагающее, что приемы деятельности могут быть разной степени сложности и
обобщенности. Они состоят из большого числа действий, выполнение которых
приводит к применению алгоритмов на отдельных этапах работы.

Такой подход к преподаванию математики в основной школе определяет условия
для формирования у учащихся навыков, позволяющих в старших классах успешно
изучать базовый курс “Информатики и ИКТ”. Применение алгоритмов в старших
классах, по мнению некоторых учителей, отбивает творческий подход к решению
задач, но с другой стороны, твердое знание основных задач курса и умение их
решать, является твердым фундаментом для активизации самостоятельной и
творческой работы учащихся.

Список литературы

1. Кухарев Н.В. На пути к профессиональному совершенству. – М.:
   Просвещение, 1990.
2. Епишева О.Б. Крутич В.И. Учить школьников учиться математике. –
   М.: Просвещение, 1990.
3. Сост. Глейзер Г.Д. Повышение эффективности обучения математике в
   школе. – М. : Просвещение, 1991.
4. Груденов Я.И. Совершенствование методики работы учителя
   математики. – М.: Просвещение, 1990.
5. Байдак В.А. и др. Формирование алгоритмической культуры у
   учащихся. – М.: Просвещение, 1989.

НОУ ИНТУИТ | Лекция | Нормальные алгоритмы Маркова

Аннотация: Определение нормального алгоритма Маркова и его выполнение. Возможности нормальных алгоритмов Маркова и тезис Маркова. Методика разработки нормальных алгоритмов Маркова.

Определение нормального алгоритма и его выполнение

В середине прошлого века выдающийся русский математик А.А. Марков ввел понятие нормального алгоритма (алгорифма) с целью уточнения понятия «алгоритм», что позволяет решать задачи по определению алгоритмически неразрешимых проблем. Позже это понятие получило название нормального алгоритма Маркова (НАМ). Язык НАМ, с одной стороны, намеренно беден, что необходимо для цели введения понятия «алгоритм». Однако, с другой стороны, идеи НАМ положены в основу большой группы языков программирования, получивших название языки логического программирования, которые являются темой данного пособия.

Для определения НАМ вводится произвольный алфавит — конечное непустое множество символов, при помощи которых описывается алгоритм и данные. В алфавит также включается пустой символ, который мы будем обозначать греческой буквой . Под словом понимается любая последовательность непустых символов алфавита либо пустой символ, который обозначает пустое слово.

Всякий НАМ определяется конечным упорядоченным множеством пар слов алфавита, называемых подстановками . В паре слов подстановки левое (первое) слово непустое, а правое (второе) слово может быть пустым символом. Для наглядности левое и правое слово разделяются стрелкой. Например,

2. intuit.ru/2010/edi»>

В качестве данных алгоритма берется любая непустая строка символов. Работа НАМ состоит из последовательности совершенно однотипных шагов. Шаг работы алгоритма может быть описан следующим образом:

1. В упорядоченной последовательности подстановок ищем самую первую подстановку, левое слово которой входит в строку данных.
2. В строке данных ищем самое первое (левое) вхождение левого слова найденной подстановки.
3. Это вхождение в строке данных заменяем на правое слово найденной подстановки (преобразование данных).

Шаг работы алгоритма повторяется до тех пор, пока

• либо не возникнет ситуация, когда шаг не сможет быть выполнен из-за того, что ни одна подстановка не подходит ( левое слово любой подстановки уже не входит в строку данных ) — правило остановки ;
• intuit.ru/2010/edi»>либо не будет установлено, что процесс подстановок не может остановиться.

В первом случае строка данных, получившаяся при остановке алгоритма, является выходной (результатом) и алгоритм применим к входным данным, а во втором случае алгоритм не применим к входным данным.

Так, определенный выше в примере нормальный алгоритм Маркова преобразует слово в слово следующим образом (над стрелкой преобразования мы пишем номер применяемой подстановки, а в преобразуемой строке подчеркиваем левое слово применяемой подстановки ):

а при преобразовании слова abbc этот же алгоритм будет неограниченно работать, так как имеет место цикличное повторение данных:

Таким образом, всякий нормальный алгоритм Маркова определяет функцию, которую мы назовем нормальной (или вычислимой по Маркову), которая может быть частичной и которая в области определения входному слову ставит в соответствие выходное слово.

Возможности нормальных алгоритмов и тезис Маркова

Прежде всего рассмотрим возможности реализации арифметических операций с помощью нормальных алгоритмов Маркова. Сначала обратим внимание на одно обстоятельство, связанное с работой любого НАМ: нужно либо вводить дополнительное правило остановки работы нормального алгоритма (иначе в примере увеличения числа на 1 алгоритм продолжит работу и снова будет увеличивать полученный результат еще на 1 и т.д. неограниченное число раз), либо перед началом работы нормального алгоритма добавлять к входной строке специальные символы, отличные от других символов строки, которые учитываются подстановками алгоритма в начале его работы и которые удаляются в конце работы алгоритма. Мы будем придерживаться второго способа, как и одна из наиболее успешных реализаций нормальных алгоритмов Маркова в виде языка программирования Рефал. В качестве добавляемого символа возьмем символ «@».

intuit.ru/2010/edi»>Пример 1. Рассмотрим простейшую операцию увеличения десятичного числа на 1. В этом случае почти всегда необходимо увеличить последнюю цифру на 1, а последняя цифра отличается тем, что после нее идет символ «@». Поэтому первыми подстановками должны быть подстановки типа

Но если это цифра 9, то ее нужно заменить 0 и увеличение на 1 перенести в предыдущий разряд. Этому отвечает подстановка

Наконец, если число начинается с 9 и перед этой цифрой нужно поставить 1, то этому будет отвечать подстановка

а если это не так, то в конце работы алгоритма символы @ надо стереть, что выполнит подстановка

Таким образом, мы получаем следующий НАМ увеличения десятичного числа на 1:

Приведем работу построенного алгоритма для чисел 79 и 99:

intuit.ru/2010/edi»>Аналогичным образом разрабатывается нормальный алгоритм Маркова для уменьшения числа на 1 (см. упражнение 1.3.1).

Пример 2. Прежде, чем перейти к другим арифметическим операциям, рассмотрим как довольно типичный пример, используемый часто в других алгоритмах, алгоритм копирования двоичного числа. В этом случае прежде всего исходное и скопированное числа разделим символом «*». В разрабатываемом алгоритме мы будем копировать разряды числа по очереди, начиная с младшего, но нужно решить 2 проблемы: как запоминать значение символа, который мы копируем, и как запоминать место копируемого символа. Для решения второй проблемы используем символ «!», которым мы будем определять еще не скопированный разряд числа, после которого и стоит этот символ. Для запоминания значения копируемого разряда мы будем образовывать для значения 0 символ «a», а для значения 1 — символ «b». Меняя путем подстановок эти символы «a» или «b» с последующими, мы будем передвигать разряды «a» или «b» в начало копируемого числа (после «*»), но для того, чтобы пока не происходило копирование следующего разряда справа, мы перед передвижением разряда временно символ «!» заменим на символ «?», а после передвижения сделаем обратную замену. После того как все число окажется скопированным в виде символов «a» и «b», мы заменим эти символы на 0 и 1 соответственно. В результате нормальный алгоритм копирования двоичного числа можно определить следующей последовательностью подстановок:

Продемонстрируем работу алгоритма для числа 10:

Для построения алгоритма сложения двух чисел можно использовать идею уменьшения одного числа на 1 с последующим увеличением другого числа на 1 и повторением этого до тех пор, пока уменьшаемое число не исчезнет после того, как станет равным 0. Но можно использовать и более сложную идею поразрядного сложения с переносом 1 в разряд слева. Построение этих алгоритмов, а также алгоритмов вычитания, умножения и деления выделено для самостоятельной работы в упражнениях 2 — 9 (см. 1.3).

Приведенные примеры показывают также возможности аппарата нормальных алгоритмов Маркова по организации ветвления и цикличных процессов вычисления.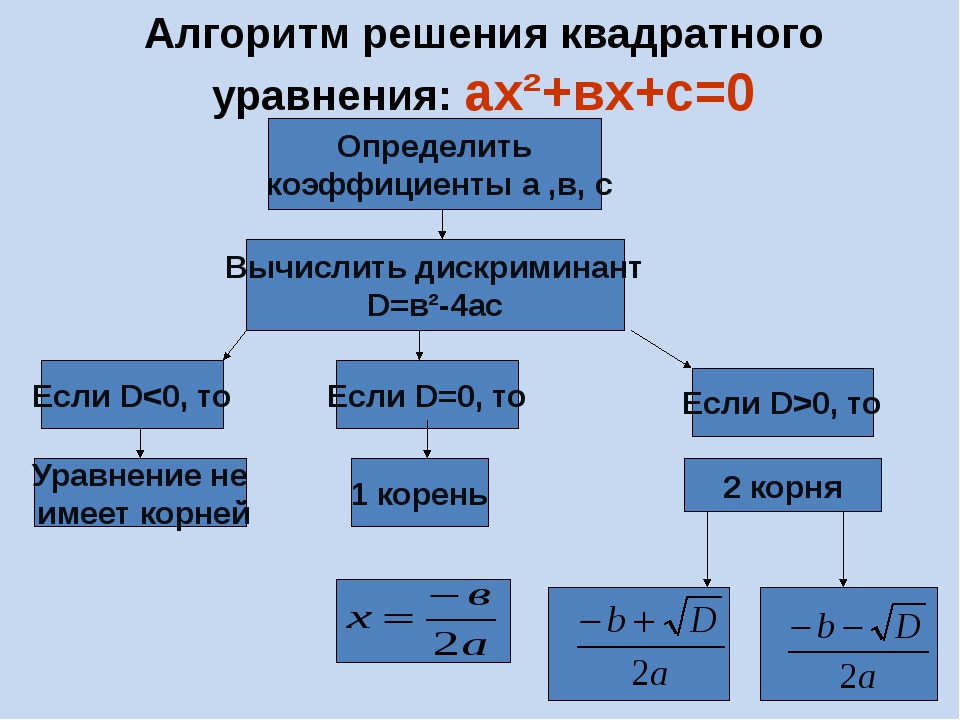 Это показывает, что всякий алгоритм может быть нормализован
т. е. задан нормальным алгоритмом Маркова. В этом и состоит тезис Маркова, который следует понимать как определение алгоритма.

Вместе с тем построение алгоритма в последнем приведенном примере подсказывает следующую методику разработки НАМ:

1. Произвести декомпозицию (разбиение на части) строящегося алгоритма. В примере это следующие части:
   1. разделение исходного числа и копии;
   2. копирование разряда;
   3. повторение предыдущей части до полного копирования всех разрядов.
2. Решение проблем реализации каждой части. В примере это следующие проблемы:
   1. запоминание копируемого разряда — разряд 1 запоминается как символ «a», а разряд 0 — как символ «b»;
   2. запоминание места копируемого разряда — пометка еще не скопированного символа дополнительным символом «!» с заменой его на символ «?» при передвижении копируемого разряда и обратной заменой после передвижения.
3. Если часть для реализации является сложной, то она также подвергается декомпозиции.
4. Сборка реализации в единый алгоритм.

Упражнения

1. Определите нормальный алгоритм, который уменьшает число на единицу.
2. Определите нормальный алгоритм сложения двух двоичных чисел методом уменьшения одного числа на 1 и увеличением другого числа на 1 до тех пор, пока уменьшаемое число не станет равным 0.
3. Определите нормальный алгоритм логического сложения двух двоичных чисел.
4. Определите нормальный алгоритм логического умножения двух двоичных чисел.
5. Определите нормальный алгоритм сложения по модулю 2 двух двоичных чисел.
6. intuit.ru/2010/edi»>Определите нормальный алгоритм поразрядного сложения двух двоичных чисел.
7. Определите нормальный алгоритм вычитания двоичных чисел.
8. Определите нормальный алгоритм умножения двух двоичных чисел столбиком.
9. Определите нормальный алгоритм деления двух двоичных чисел с определением частного и остатка.
10. Определите нормальный алгоритм вычисления наибольшего общего делителя двух двоичных чисел.
11. Определите нормальный алгоритм вычисления наименьшего общего кратного двух двоичных чисел.

Математика и гармония: Математические алгоритмы

Алгоритмы арифметических действий:
Алгоритм умножения числа на произведение (сочетательное свойство умножения)
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Алгоритм вычитания суммы
Для того чтобы вычесть сумму из числа, можно вначале вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое;
Алгоритм вычитания числа из суммы
Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить второе слагаемое.
Алгоритм умножения числа на произведение (сочетательное свойство умножения)
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Алгоритм умножения суммы на число (распределительное тельное свойство умножения относительно сложения)
Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения.
Алгоритм умножения разности на число (распределительное тельное свойство умножения относительно вычитания)
Для того, чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.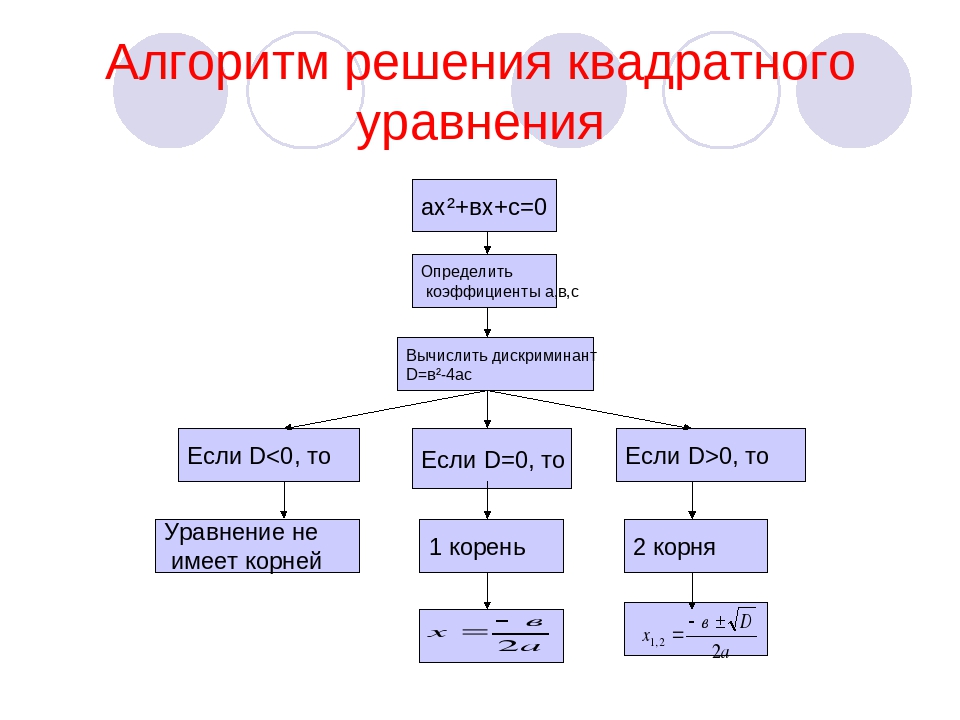
Алгоритмы при решении уравнений:
Алгоритм нахождения неизвестного слагаемого
Чтобы найти неизвестное слагаемое, надо их суммы вычесть известное слагаемое.
Алгоритм нахождения неизвестного уменьшаемого
Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.
Алгоритм нахождения неизвестного вычитаемого
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть и разность.
Алгоритм нахождения неизвестного множителя
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Алгоритм нахождения неизвестного делимого
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Алгоритм нахождения неизвестного делителя
Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Алгоритм решения задач с помощью уравнения
1. Прочитать внимательно условие задачи;
2. Записать кратко условие задачи, записав все величины (единицы их измерения) , названные в задаче, установив связи и зависимости между ними;
3.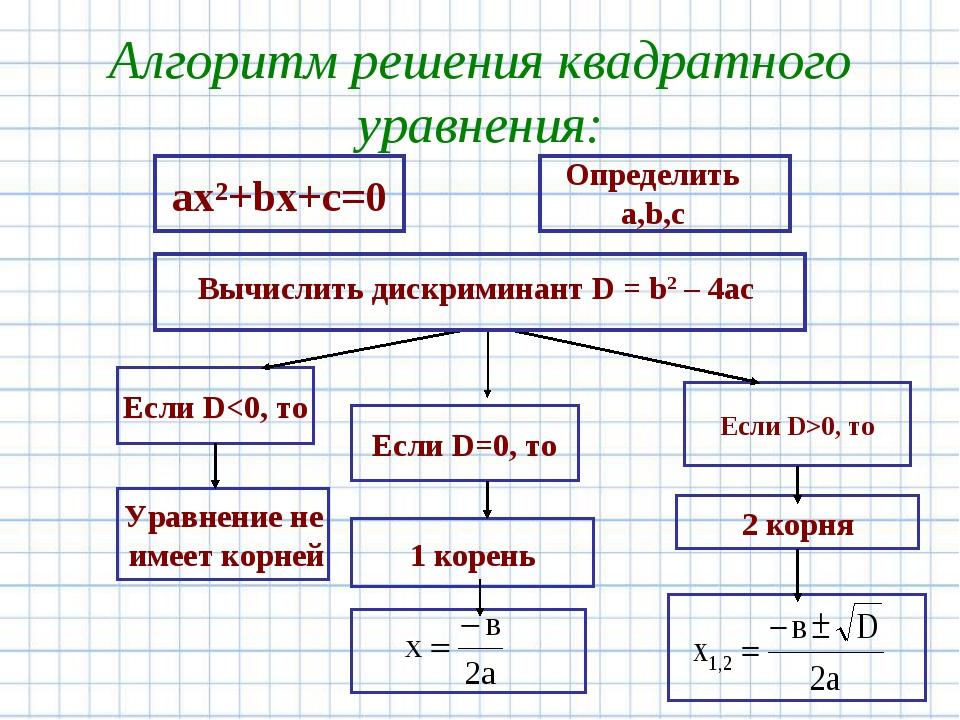 Выбрать неизвестное задачи;
4. Выразить остальные величины задачи, установить связи их с неизвестным задачи;
5. Составить уравнение задачи, обосновав его условием задачи;
6. Решить уравнение;
7. Сделать проверку;
8. Выписать ответ.
Алгоритм выполнения порядка действий
1. Если в выражении нет скобок, и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой (сложение и вычитание) и второй (умножение и деление) ступени и в нем нет скобок, то сначала выполняют действия второй ступени, а потом – действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Алгоритмы для обыкновенных дробей
Алгоритм сравнения дробей с одинаковыми знаменателями
а) Выбрать наибольшую дробь с одинаковыми знаменателями ту, у которой больше числитель;
б) Выбрать наименьшую дробь с одинаковыми знаменателями ту, у которой меньше числитель.
Алгоритмы сложения и вычитания дробей с одинаковыми знаменателями
а) При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатели оставляют тот же;
б) При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатели оставляют тот же.
Алгоритмы представления смешанного числа в виде неправильной дроби
1. Умножить его целую часть на знаменатель дробной части;
2. К полученному произведению прибавить числитель дробной части;
3. Записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

Алгоритмы для десятичных дробей
Алгоритм сложения (вычитания) десятичных дробей
Чтобы сложить (вычесть) десятичные дроби, нужно:
1. уравнять в этих дробях количество знаков после запятой;
2. записать их друг под другом так, чтобы запятая была записана под запятой;
3. выполнить сложение (вычитание), не обращая внимания на запятую;
4. поставить в ответе запятую под запятой в данных дробях.

Алгоритм округления десятичных дробей
а) Если первая отброшенная или замененная нулём цифра равна 5, 6,7, 8, 9, то стоящую перед ней цифру увеличивают на 1.
а) Если первая отброшенная или замененная нулём цифра равна 0, 1, 2, 3, 4, то стоящую перед ней цифру оставляют без изменения.
Алгоритм умножения десятичной дроби на натуральное число
Чтобы умножить десятичную дробь на натуральное число, надо:
1. умножить её на это число, не обращая внимания на запятую;
2. в полученном произведении отделить запятой столько цифр справа , сколько их отделено запятой в десятичной дроби.
Алгоритм умножения десятичной дроби на 10, 100, 1000, ….
Чтобы умножить десятичную дробь на 10, 100, 1000, … надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоят в множителе после единицы.
Алгоритм деления десятичных дробей на натуральные числа
Чтобы разделить десятичную дробь на натуральное число, надо:
1. разделить дробь на это число, не обращая внимания на запятую;
2. поставить в частном запятую, когда кончится деление целой части.
Алгоритм деления десятичной дроби на 10, 100, 1000, ….
Чтобы разделить десятичную дробь на 10, 100, 1000, …надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
Алгоритм умножения десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
1. выполнить умножение, не обращая внимания на запятые;
2. отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе;
3. если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
Алгоритм умножения числа на 0,1; 0,01, 0,001 …
Для того чтобы умножить число на 0,1; 0,01, 0,001 надо:
1. разделить его на 10,100, 1000;
2. перенести запятую на столько цифр, сколько нулей стоит перед единицей в множителе.
Алгоритм деления числа на десятичную дробь
Для того чтобы разделить число на десятичную дробь, надо:
1. В делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2. после этого выполнить деление на натуральное число.
Алгоритм деления числа на 0,1; 0,01, 0,001
Для того чтобы разделить десятичную дробь на 0,1; 0,01, 0,001…, надо:
перенести в ней запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей ( то есть умножить её на 10, 100, 1000.
Алгоритм нахождения среднего арифметического
Для нахождения среднего арифметического нескольких чисел надо:
1.найти сумму этих чисел;
2. разделить полученную сумму на число слагаемых;
3. выписать частное в ответ.
Алгоритм обращения десятичной дроби в проценты:
Чтобы обратить десятичную дробь в проценты надо умножить дробь на 100.
Алгоритм перевода процентов в десятичную дробь
Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.

Признаки делимости
Признак делимости на 10
Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Например:
100; 1000; 100000 и т.п.
Признак делимости на 5
Если запись натурального числа оканчивается цифрами 0 и 5, то это число делится без остатка на 5.
Например:
45; 55; 15; 10; 10000 и т.п.
Признак делимости на 2
Если запись натурального числа оканчивается четной цифрой, то это число четно и делится без остатка на 2.
Например:
32; 12; 224; 2098 и т. п.
Признак делимости на 3
Если сумма цифр числа делится на 3, то и число делится на 3.
Например:
15; 273; 474; 765; и т.п.
Признак делимости на 9
Если сумма цифр числа делится на 9, то и число делится на 9.
783; 549; 1233; 27954; и т.п.

Разложение на простые множители
Алгоритм нахождения НОД (наибольшего общего делителя)
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
1. разложить их на простые множители;
2. из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3. найти произведение оставшихся множителей.
Например:
48 = 2*2*2*2*3; 36 = 2*2*3*3; НОД(48;36)= 2*2*3 = 12.

Алгоритм нахождения НОК (наименьшего общего кратного)
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1. разложить их на простые множители;
2. выписать множители, входящие в разложение одного из чисел;
3. добавить к ним недостающие множители из разложений остальных чисел;
4. найти произведение оставшихся множителей.
Например:
48 = 2*2*2*2*3; 36 = 2*2*3*3; НОК(48;36)= 2*2*2*2*3*3 = 144.

Алгоритмы для обыкновенных дробей
Алгоритм сокращения дробей
Для того чтобы сократить дробь необходимо и числитель и знаменатель дроби разделить на их общий делитель, отличный от 1.

Алгоритм приведения дробей к общему знаменателю
Чтобы привести дроби к наименьшему общему знаменателю надо:
1. Найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2. разделить наименьший общий множитель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на её дополнительный множитель;

Алгоритм сравнения, сложения, вычитания
дробей с разными знаменателями
Чтобы сравнить (сложить, вычесть) дроби с разными знаменателями надо:
1. привести данные дроби к наименьшему общему знаменателю;
2. сравнить, сложить, вычесть полученные дроби.

Алгоритм сложения смешанных чисел
Чтобы сложить смешанные числа надо:
1. привести дробные части этих чисел к наименьшему общему знаменателю;
2. отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части.

Алгоритм вычитания смешанных чисел
Чтобы вычесть смешанные числа надо:
1. привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть;
2. отдельно выполнить вычитание целых частей и отдельно дробных частей.

Алгоритм умножения дроби на натуральное число
Чтобы умножить дробь на натуральное число , надо её числитель умножить на это число, а знаменатель оставить без изменения.

Алгоритм умножения дроби на дробь
Чтобы умножить дробь на дробь надо:
1. найти произведение числителей и произведение знаменателей этих дробей;
2. первое произведение записать числителем, а второе – знаменателем.

Алгоритм умножения смешанных чисел
Чтобы умножить смешанные числа надо:
1.их записать в виде неправильных дробей;
2.воспользоваться правилом умножения дробей.

Алгоритм нахождения дроби от числа
Чтобы найти дробь от числа, надо умножить число на эту дробь.

Алгоритм умножения смешанного числа на натуральное число
(применение распределительного свойства умножения)
Чтобы умножить смешанное число на натуральное число надо:
1. умножить целую часть на натуральное число;
2. умножить дробную часть на это натуральное число;
3. сложить полученные результаты.

Алгоритм деления обыкновенных дробей
Чтобы разделить одну дробь на другую надо:
1. делитель представить в виде обратной дроби;
2. провести умножение делимого и преобразованного делителя.

Алгоритм нахождения числа по его дроби
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
Арифметические действия с положительными и отрицательными числами
Алгоритм сложения отрицательных чисел
Чтобы сложить два отрицательных числа, надо:
1. сложить их модули;
2. поставить перед полученным числом знак « — ».
Например: — 8,7 + (- 3.5) = — (8,7 +3.5) = — 12,2.

Алгоритм сложения чисел с разными знаками
Чтобы сложить два числа с разными знаками, надо:
1. из большего модуля слагаемых вычесть меньший;
2. поставить перед полученным числом знак того слагаемого , модуль которого больше.
Например: 6,1 + (- 4,2) = + (6,1 — 4,2) = 1,9.

Алгоритм нахождения длины отрезка на координатной прямой
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

Алгоритм умножения чисел с разными знаками
Чтобы перемножить два числа с разными знаками, надо:
1.перемножить модули этих чисел;
2. поставить перед полученным числом знак « — ».
Например: (-1,2) * 0,3 = — (1,2 * 0,3) = — 0,36.

Алгоритм умножения отрицательных чисел
Чтобы перемножить два числа с отрицательными знаками, надо перемножить их модули.
Например: (-3,2) * (-9) =  3,2 * 9 = 28,8.

Алгоритм деления отрицательного числа на отрицательное
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
Например: — 4,5 : (-1,5) = 4,5 : 1,5 = 3.

Алгоритм деления чисел с разными знаками
При делении чисел с разными знаками, надо:
1. разделить модуль делимого на модуль делителя;
2. поставить перед полученным числом знак « — ».
Например: 3,6 : (-3) = — (3,6 : 3) = — 1,2.

Алгоритмы раскрытия скобок
а) Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».
Например: — 2,87 + (2,87 – 7,639) = — 2,87 + 2,87 – 7,639 = 0 -7,639 = -7,639.
б). Если перед скобками стоит знак « — », то надо заменить этот знак на « + »,
поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Например: 16 – (10 – 18 + 12) = 16 + ( — 10 + 18 – 12) = 16 — 10 + 18 — 12 = 12.

Учебно-методическое обеспечение дисциплины

%PDF-1.6 %
1 0 obj >/PageMode/UseOutlines/Outlines 6 0 R/Metadata 4 0 R/Pages 2 0 R/PageLayout/SinglePage/OCProperties>/OCGs[10 0 R]>>/OpenAction 3677 0 R/StructTreeRoot 30 0 R/Type/Catalog>> endobj 6 0 obj > endobj 4 0 obj >stream
2008-11-26T07:45:01+05:002008-11-25T12:13:42+05:002008-11-26T07:45:01+05:00Acrobat PDFMaker 8. 1 for Wordapplication/pdf

uuid:03efb905-b856-46a4-b671-def177646bf2uuid:7679e8e2-ce39-421a-907d-59cf0b0a7c99Acrobat Distiller 8.1.0 (Windows)

endstream endobj 2 0 obj > endobj 3677 0 obj > endobj 30 0 obj > endobj 5 0 obj > endobj 130 0 obj > endobj 131 0 obj > endobj 132 0 obj > endobj 309 0 obj > endobj 1086 0 obj > endobj 1803 0 obj > endobj 2857 0 obj > endobj 1083 0 obj > endobj 2854 0 obj > endobj 1084 0 obj > endobj 3666 0 obj > endobj 3566 0 obj > endobj 1085 0 obj > endobj 138 0 obj > endobj 1087 0 obj > endobj 1804 0 obj > endobj 2858 0 obj > endobj 3569 0 obj > endobj 3667 0 obj > endobj 311 0 obj > endobj 310 0 obj > endobj 139 0 obj > endobj 140 0 obj > endobj 135 0 obj > endobj 136 0 obj > endobj 137 0 obj > endobj 2855 0 obj > endobj 2856 0 obj > endobj 1800 0 obj > endobj 1801 0 obj > endobj 1802 0 obj > endobj 307 0 obj > endobj 308 0 obj > endobj 133 0 obj > endobj 134 0 obj > endobj 3567 0 obj > endobj 3568 0 obj > endobj 3564 0 obj > endobj 3565 0 obj > endobj 3660 0 obj > endobj 3662 0 obj > endobj 3664 0 obj > endobj 3665 0 obj > endobj 3611 0 obj > endobj 3583 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 2943 0 obj > endobj 3588 0 obj >stream
Hlj0yZdKcC)IZP4’Qҷl$SWsw{MƖ|cq{{ww?^P7QA

jH
H RNTѾ»dEjõu3ėwL܉\(t K^$#QlʢN
}mura+4ʊlJY/»YF;ITjkr. oG3UBd\d

математических алгоритмов — GeeksforGeeks

Последние статьи по математическим алгоритмам

Тема:

GCD и LCM:

Подробнее >>

Простое факторизация и делители:

Подробнее >>

Числа Фибоначчи:

Подробнее >>

Модульная арифметика:

Подробнее >>

Каталонские номера:

Функция Эйлера Totient:

nCr Вычисления:

Китайская теорема об остатке:

Факториал:

Подробнее >>

Простые числа и тесты на простоту:

Подробнее >>

Теория множества:

Алгоритмы сита:

Подробнее >>

Делимость и большие числа:

Подробнее >>

Серия:

1. Последовательность жонглера
2. Последовательность Падована
3. Последовательность аликвот
4. Последовательность Мозера-де Брюйна
5. Последовательность Штерна-Броко
6. Последовательность Ньюмана-Конвея
7. Последовательность Сильвестра
8. Последовательность Рекамана
9. Обильное число
10. Шестиугольное число
11. Номера эмиратов
12. Теорема Никомаха (сумма k-й группы нечетных положительных чисел)
13. Сумма попарных произведений
14. Треугольное число в квадрате (Сумма кубов)
15. Квадратное пирамидальное число (Сумма квадратов)
16. Программа для вывода суммы заданного n-го члена
17. Сумма рядов с чередующимися знаками квадратов AP
18. Программа для суммы cos (x) серии
19. Сумма диапазона в серии сначала нечетных, затем четных натуральных чисел
20. Сумма последовательности 2, 22, 222, ………
21. Сумма ряда 5 + 55 + 555 +. 2
22. Сумма рядов 2/3 — 4/5 + 6/7 — 8/9 + ——- до слагаемых
23. Сумма ряда 0,6, 0,06, 0,006, 0,0006,… до n членов
24. n-й член в ряду 2, 12, 36, 80, 150….
25. Программа для печати тетраэдрических чисел до N-го члена

Подробнее >>

Число цифр:

Подробнее >>

Треугольники:

Алгебра:

квантовых алгоритмов через линейную алгебру

Главная страница

— Алгоритмы соревновательного программирования

Главная страница — Алгоритмы соревновательного программирования

Цель этого проекта — перевод замечательного ресурса
http: // e-maxx.ru / algo, который предоставляет описания многих алгоритмов
и структуры данных, особенно популярные в области конкурентного программирования.
Кроме того, мы хотим улучшить полученные знания, расширив статьи
и добавление новых статей в сборник.

Для аналогичного проекта, который переводит сборник статей на португальский язык, посетите https://cp-algorithms-brasil.com.

Статьи

Алгебра

• Основы
• Простые числа
• Теоретико-числовые функции
• Модульная арифметика
• Системы счисления
• Разное

Структуры данных

• Основы
• Деревья
• Продвинутый

Динамическое программирование

Обработка строк

• Основы
• Продвинутый
• Задачи

Линейная алгебра

Комбинаторика

• Основы
• Методы
• Задачи

Численные методы

Геометрия

• Основные операции
• Полигоны
• Корпус выпуклый
• Подметальная линия
• Разное

Графики

• Обход графика
• Соединяемые компоненты, мосты, точки сочленения
• Кратчайшие пути из одного источника
• Кратчайшие пути всех пар
• Остовные деревья
• циклов
• Самый низкий общий предок
• Потоки и связанные с ними проблемы

Операции над многочленами и рядами

В этой статье мы рассмотрим общие операции, которые вам, вероятно, придется делать, если вы имеете дело с многочленами. n $ такое, что $ a_n \ neq 0 $.

• Для простоты мы будем писать $ A $ вместо $ A (x) $ везде, где это возможно, что будет понятно из контекста.
• Определим степень полинома $ A $ как $ \ deg A = n $. Удобно сказать, что $ \ deg A = — \ infty $ при $ A (x) = 0 $.
• Для произвольных многочленов $ A $ и $ B $ выполняется $ \ deg AB = \ deg A + \ deg B $.
• Многочлены образуют евклидово кольцо, что означает, что для любых многочленов $ A $ и $ B \ neq 0 $ мы можем однозначно представить $ A $ в виде: $$ A = D \ cdot B + R, ~ \ deg R <\ deg B .$$ Здесь $ R $ называется остатком от $ A $ по модулю $ B $, а $ D $ называется частным.
• Если $ A $ и $ B $ имеют одинаковый остаток по модулю $ C $, они считаются эквивалентными по модулю $ C $, что обозначается как: $$ A \ Equiv B \ pmod {C} $$
• Для любого линейного полинома $ x-r $ выполняется: $$ A (x) \ Equiv A (r) \ pmod {x-r} $$
• В частности: $$ A (r) = 0 \ iff A (x) \ Equiv 0 \ pmod {xr} $$ Это означает, что $ A $ делится на $ xr $ $ \ iff $ $ A (r) = 0 $. k} $

Базовая реализация

Здесь вы можете найти базовую реализацию алгебры полиномов.

Он поддерживает все тривиальные операции и некоторые другие полезные методы. Основной класс — poly для многочленов с коэффициентами класса T .

Все арифметические операции + , - , * , % Поддерживаются и /, % и / обозначают остаток и частное при целочисленном делении.

Существует также класс modular для выполнения арифметических операций с остатками по модулю простого числа m .k}} $ со сложностью: $$ T (n) = T (n / 2) + O (n \ log n) = O (n \ log n) $$

Дивизия с остатком

Рассмотрим два многочлена $ A (x) $ и $ B (x) $ степеней $ n $ и $ m $. Как было сказано ранее, вы можете переписать $ A (x) $ как:

$$ A (x) = B (x) D (x) + R (x), \ deg R <\ deg B $$

Пусть $ n \ geq m $, тогда вы сразу поймете, что $ \ deg D = n — m $ и что ведущие $ n-m + 1 $ коэффициенты $ A $ не влияют на $ R $.

Это означает, что вы можете восстановить $ D (x) $ из наибольших $ n-m + 1 $ коэффициентов для $ A (x) $ и $ B (x) $, если рассматривать это как систему уравнений.{2a}}} $

Таким образом, зная, как инвертировать произвольный многочлен и как быстро вычислить $ F (Q_k) $, мы можем найти $ n $ коэффициентов $ P $ со сложностью: $$ T (n) = T (n / 2) + f (n) $$ Где $ f (n) $ — это максимум $ O (n \ log n) $, необходимый для инвертирования ряда и времени, необходимого для вычисления $ F (Q_k) $, которое обычно также равно $ O (n \ log n) $.

Логарифм

Для функции $ \ ln P (x) $ известно, что: $$ \ boxed {(\ ln P (x)) ‘= \ dfrac {P’ (x)} {P (x)}} $$
Таким образом, мы можем вычислить $ n $ коэффициентов для $ \ ln P (x) $ в $ O (n \ log n) $.k $.

Он дает нам алгоритм $ O (n \ log n) $, когда вам нужно вычислить значения в степенях $ z $, таким образом, вы можете вычислить ДПФ для не степеней двойки.

Многоточечная оценка

Предположим, вам нужно вычислить $ A (x_1), \ dots, A (x_n) $. Как упоминалось ранее, $ A (x) \ Equiv A (x_i) \ pmod {x-x_i} $. Таким образом, вы можете сделать следующее:

1. Вычислить сегментное дерево такое, что в сегменте $ [l, r) $ стоит произведение $ P_ {l, r} (x) = (x-x_l) (x-x_ {l + 1}) \ dots ( х-х_ {г-1}) $.2 n) $ с подходом «разделяй и властвуй»:

   Рассмотрим $ P (x) = (x-x_1) \ dot

   Алгебра

   Онлайн-заметки Павла

   Примечания

   Быстрая навигация

   Скачать

   • Перейти к
   • Примечания

   • Проблемы с практикой

   • Проблемы с назначением

   • Показать / Скрыть
   • «> Показать все решения / шаги / и т. Д.
   • Скрыть все решения / шаги / и т. Д.
   • Разделы
   • Предварительные сведения Введение
   • Разделы
   • Предварительные условия
   • Классы
   • Алгебра

   • Исчисление I

   • Исчисление II

   • Исчисление III

   • Дифференциальные уравнения

   • Дополнительно

   • Алгебра и триггерный обзор

   • Распространенные математические ошибки

   • Праймер для комплексных чисел

   • Как изучать математику

   • Шпаргалки и таблицы

   • Разное
   • Свяжитесь со мной
   • Справка и настройка MathJax
   • Мои студенты
   • Заметки Загрузки
   • Полная книга
   • Practice Problems Загрузок
   • Полная книга — Только проблемы
   • Полная книга — Решения
   • Проблемы с назначением Загрузок
   • Полная книга
   • Прочие товары
   • Получить URL для загружаемых элементов
   • Распечатать страницу в текущем виде (по умолчанию)
   • Показать все решения / шаги и распечатать страницу
   • Скрыть все решения / шаги и распечатать страницу
   • Дом
   • Классы
   • Алгебра
     • Предварительные мероприятия
       • Целочисленные экспоненты
       • Рациональные экспоненты
       • Радикалы
       • Полиномы
       • Факторинговые полиномы
       • Рациональные выражения
       • Комплексные числа
     • Решение уравнений и неравенств
       • Решения и наборы решений
       • Линейные уравнения
       • Приложения линейных уравнений
       • Уравнения с более чем одной переменной
       • Квадратные уравнения — Часть I
       • Квадратные уравнения — Часть II
       • Квадратные уравнения: сводка
       • Приложения квадратных уравнений
       • Уравнения, сводимые к квадратичным в форме
       • Уравнения с радикалами
       • Линейные неравенства
       • Полиномиальные неравенства
       • Рациональные неравенства
       • Уравнения абсолютных значений
       • Неравенства абсолютных значений
     • Графики и функции
       • Графики
       • Строки
       • Круги
       • Определение функции
       • Графические функции
       • Комбинирование функций
       • Обратные функции
     • Общие графы
       • Прямые, окружности и кусочные функции
       • Параболы
       • Эллипсы
       • Гиперболы
       • Разные функции
       • Преобразования
       • Симметрия
       • Рациональные функции
     • Полиномиальные функции
       • Делящие многочлены
       • Нули / корни многочленов

   Линейная алгебра для глубокого обучения. Математика, стоящая за каждым глубоким обучением… | Вихар Курама

   Линейная алгебра, вероятность и исчисление — это «языки», на которых сформулировано машинное обучение. Изучение этих тем будет способствовать более глубокому пониманию лежащих в основе алгоритмических механизмов и позволит разрабатывать новые алгоритмы.

   Если ограничиваться меньшими уровнями, за глубоким обучением стоит математика. Поэтому очень важно понимать основы линейной алгебры, прежде чем начинать ее глубокое обучение и программирование.

   src

   Основными структурами данных, лежащими в основе глубокого обучения, являются скаляры, векторы, матрицы и тензоры. Программно давайте решим все основные задачи линейной алгебры, используя их.

   Скаляры представляют собой отдельных чисел и являются примером тензора порядка 0 -го порядка . Запись x ∈ ℝ означает, что x — скаляр, принадлежащий набору вещественных чисел real.

   В глубоком обучении есть разные наборы чисел. ℕ представляет собой набор натуральных чисел (1,2,3,…).ℤ обозначает целые числа, которые объединяют положительные, отрицательные и нулевые значения. ℚ представляет собой набор рациональных чисел, которые можно выразить дробью двух целых чисел.

   Несколько встроенных скалярных типов: int , float , сложный , байта , Unicode в Python. В библиотеке Python In NumPy есть 24 новых фундаментальных типа данных для описания различных типов скаляров. Для получения информации о типах данных обратитесь к документации здесь.

   Определение скаляров и нескольких операций в Python:

   Следующий фрагмент кода объясняет несколько арифметических операций над скалярами.

     
     
    12,5 
    -2,5 
    37,5 
    0,6666666666666666 

   Следующий фрагмент кода проверяет, является ли данная переменная скалярной или нет.

    True 
    False 
    True 

   Векторы — это упорядоченные массивы одиночных чисел, являющиеся примером тензора 1-го порядка. 3 часто используется для математического представления нашего реального представления о трехмерном пространстве.

   Чтобы явно идентифицировать необходимый компонент вектора, скалярный элемент вектора -й записывается как x [i].

   В глубоком обучении векторы обычно представляют собой векторы признаков, а их исходные компоненты определяют, насколько актуальна конкретная функция. Такие элементы могут включать связанную важность интенсивности набора пикселей в двумерном изображении или исторические значения цен для поперечного сечения финансовых инструментов.

   Определение векторов и нескольких операций в Python:

     
    [1, 2, 3, 4, 5, 6] 
    [5 7 9] 
     
    [-3 6 -3] 

   Матрицы представляют собой прямоугольные массивы, состоящие из чисел и являющиеся примером 2 тензоров порядка и . Если m и n — натуральные числа, то есть m, n ∈ ∈, тогда матрица m × n содержит m * n чисел с m строками и n столбцами.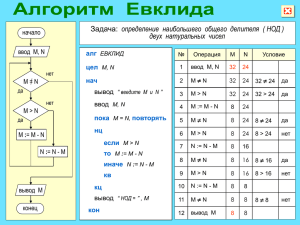

   Полная матрица m × n может быть записана как:

   Часто бывает полезно сократить отображение компонентов полной матрицы следующим выражением:

   В Python мы используем библиотеку numpy, которая помогает нам в создании многомерных массивов.Это в основном матрицы, мы используем матричный метод и передаем списки, тем самым определяя матрицу.

   $ python

    >>> import numpy as np 
    >>> x = np.matrix ([[1,2], [2,3]]) 
    >>> x 
    matrix ([[1, 2 ], 
    [2, 3]]) 
    >>> a = x.mean (0) 
    >>> матрица 
    ([[1.5, 2.5]]) 
    >>> # Нахождение среднего с 1 с матрица x. 
    >>> z = x.mean (1) 
    >>> z 
    матрица ([[1.5], 
    [2.5]]) 
    >>> z.shape 
    (2, 1) 
    >>> y = x - z 
    matrix ([[- 0.5, 0.5], 
    [-0.5, 0.5]]) 
    >>> print (type (z)) 
     
    

   Определение матриц и несколько операций в Python:

   Добавление матриц

   Матрицы могут быть добавлены к скалярам, ​​векторам и другим матрицам . У каждой из этих операций есть точное определение. Эти методы часто используются в машинном обучении и глубоком обучении, поэтому стоит с ними ознакомиться.

   Матрица-матрица сложения

   C = A + B ( Форма A и B должна быть равна )

   Метод shape возвращает форму матрицы, а add принимает два аргумента и возвращает сумму этих матриц . Если форма матриц не совпадает, выдается сообщение об ошибке, добавление невозможно.

   Матрица-скалярное сложение

   Добавляет заданный скаляр ко всем элементам данной матрицы.

   Матричное скалярное умножение

   Умножает данный скаляр на все элементы данной матрицы.

   Умножение матрицы

   Умножение A формы (mxn) и B формы (nxp) дает форму C (mxp)

   src

   Matrix Transpose

   С помощью транспонирования вы можете преобразовать вектор-строку в вектор-столбец и наоборот:

   A = [a ij ] mxn

   AT = [a ji ] n × m

   Более общая сущность тензора инкапсулирует скаляр, вектор и матрицу.

   No related posts.