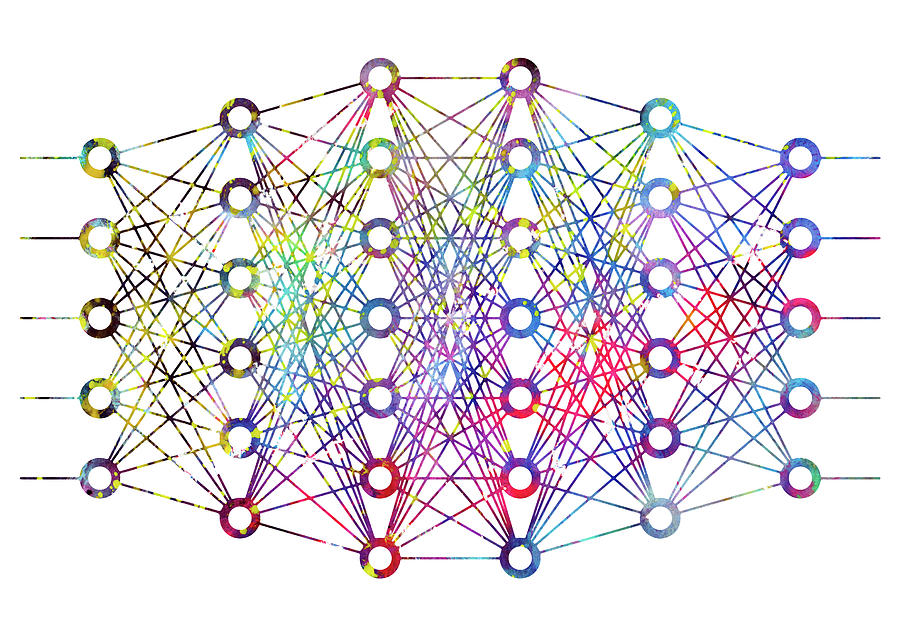
Искусственные нейронные сети однослойные сети: Нейронные сети
ПМ-ПУ :: Искусственный интеллект
Лектор к.ф.-м.н., доцент Козынченко В.А.
ВВЕДЕНИЕ
- 1. Искуственные нейронные сети: основные свойства и возможности
- Что такое искусственные нейронные сети. Краткий обзор развития искусственных нейронных сетей. Основные свойства искусственных нейронных сетей. Прикладные возможности искусственных нейронных сетей: современное состояние и перспективы на будущее.
- 2. Основы функционирования биологических нейронных сетей
- Биологический нейрон. Передача и преобразование информации в биологическом нейроне. Синаптическая передача, виды синапсов. Свойства синаптической передачи. Основные принципы организации биологических нейронных сетей.
1. ОДНОСЛОЙНЫЙ ПЕРСЕПТРОН
- 1. Понятие искусственного нейрона и его обучения.
- Модель МакКаллока-Питца. Виды активационных функций. Задача обучения нейрона. Обучающие выборки. Обучение с учителем.
- 2. Персептрон.
- Персептрон Розенблатта. Обучение по правилу персептрона. Теорема о сходимости персептрона. Однослойные сети персептронного типа.
- 3. Сигмоидальные нейроны и однослойные сети сигмоидального типа.
- Модель сигмоидального нейрона. Униполярная и биполярная функции активации и их свойства. Градиентные методы обучения сигмоидального нейрона и проблемы их практического применения. Условия сходимости алгоритма минимизации среднеквадратичной ошибки. Обучение с моментом. Однослойные сети сигмоидального типа.
- 4. Нейрон типа «адалайн».
- Модель нейрона типа «адалайн» и метод его обучения.
- 5. Персептронная представляемость.
- Проблема исключающего ИЛИ. Линейная разделяемость обучающего множества. Ограниченные возможности однослойного персептрона. Примеры. Преодоление ограничения линейной разделимости.
2. МНОГОСЛОЙНЫЙ ПЕРСЕПТРОН
- 1. Многослойный персептрон.
- Структура многослойной однонаправленной сети нейронов сигмоидального типа.
 Задача обучения многослойного персептрона. Последовательный и пакетный режимы обучения. Общая схема обучения.
Задача обучения многослойного персептрона. Последовательный и пакетный режимы обучения. Общая схема обучения. - 2. Алгоритм обратного распространения ошибки.
- Вывод формул для алгоритма обратного распространения ошибки
- 3. Градиентные методы обучения многослойного персептрона.
- Методы первого порядка. Обучение с использованием метода наискорейшего спуска. Проблемы, возникающие при использовании методов первого порядка и пути их разрешения. Обучение с моментом. Методы второго порядка. Алгоритмы переменной метрики, Левенберга-Марквардта и сопряженных градиентов. Подбор коэффициента обучения в градиентных методах обучения.
- 4. Выбор начального значения весов нейронов.
- Проблема выбора начальных значений весов нейронов. Методы глобальной оптимизации. Генетические алгоритмы.
- 5. Подбор архитектуры многослойного персептрона и персептронная представляемость. Выбор обучающего множества.
- Персептронная представляемость в случае многослойного персептрона. Теорема Колмогорова. Способность многослойного персептрона к обобщению данных и проблема избыточного обучения. Разделение обучающего множества и обучение с ранним остановом. Первоначальный подбор архитектуры сети. Методы редукции сети. Методы наращивания сети.
- 6. Обучение многослойного персептрона. Резюме.
- Этапы обучения многослойного персептрона. Проблемы обучения и пути их разрешения
- 7. Примеры использования многослойного персептрона.
- Распознавание и классификация образов. Сжатие данных. Прогнозирование. Задача аппроксимации.
3. СЕТИ РАДИАЛЬНЫХ НЕЙРОНОВ
- 1. Радиальные нейроны.
- Радиальные базисные функции. Структура радиального нейрона. Теорема Ковера о распознаваемости образов. Локальная аппроксимация радиальными функциями.
- 2. Радиальные нейронные сети.
- Структура сети радиальных нейронов. Задача обучения радиальной сети.
- 3. Методы обучения радиальных сетей и методы подбора количества нейронов.

- Проблемы обучения радиальных сетей. Гибридный алгоритм обучения. Процесс самоорганизации. Эвристические методы подбора количества нейронов. Метод ортогонализации.
- 4. Применение радиальных сетей и сравнение с многослойным персептроном.
- Сравнение сетей радиальных нейронов и многослойных персептронов. Задачи классификации образов и аппроксимации.
4. СЕТИ САМООРГАНИЗАЦИИ И СЕТИ ВСТРЕЧНОГО РАСПРОСТРАНЕНИЯ
- 1. Инстар Гроссберга.
- Инстра Гроссберга. Задачи обучения инстара с учителем и без учителя. Обучение по правилу Гроссберга. Примеры решения задач кластеризации.
- 2. Сети с самоорганизацией на основе конкуренции.
- Основные принципы построения и функционирования сетей самоорганизации на основе конкуренции. Алгоритмы обучения сетей с самоорганизацией. Обучение по правилам WTA и WTM. Обучение по правилу Кохонена. Проблема мертвых нейронов. Применение сетей самоорганизации. Сжатие и восстановление данных.
- 3. Сети встречного распространения.
- Структура сетей встречного распространения. Обучение и функционирование сетей встречного распространения. Применение сетей встречного распространения. Сжатие данных.
5. РЕКУРРЕНТНЫЕ СЕТИ АССОЦИАТИВНОЙ ПАМЯТИ
- 1. Введение в нейродинамику.
- Нейронные сети с обратными связями. Ассоциативная память. Состояния равновесия динамической системы и их устойчивость. Нейродинамические модели. Теорема Коэна-Гроссберга.
- 2. Сеть Хопфилда.
- Автоассоциативная память. Структура сети Хопфилда. Математическая модель и энергетическая функция. Устойчивость сети Хопфилда. Обучение сети Хопфилда по обобщенному правилу Хебба. Режимы обучения и распознавания сети Хопфилда. Емкость сети Хопфилда.
- 3. Сеть Хемминга.
- Структура и функционирование сети Хэмминга. Сравнение сетей Хопфилда и Хемминга. Применение сети Хемминга
- 4. Двунаправленная ассоциативная память (ВАМ).
- Гетероассоциативная память.
 Структура и функционирование сети ВАМ. Кодирование и восстановление запомненных ассоциаций. Обучение по правилу Коско. Модифицированный алгоритм обучения сети ВАМ. Модифицированная структура сети ВАМ и её функционирование. Емкость сетей ВАМ. Примеры применения сетей ВАМ.
Структура и функционирование сети ВАМ. Кодирование и восстановление запомненных ассоциаций. Обучение по правилу Коско. Модифицированный алгоритм обучения сети ВАМ. Модифицированная структура сети ВАМ и её функционирование. Емкость сетей ВАМ. Примеры применения сетей ВАМ.
6. НЕЙРОННЫЕ СЕТИ АДАПТИВНОЙ РЕЗОНАНСНОЙ ТЕОРИИ (АРТ)
Назначение и виды сетей АРТ. Архитектура и основные особенности сети АРТ1. Реализация отдельных блоков сети АРТ1. Функционирование сети АРТ1. Основные АРТ-теоремы. Применение, достоинства и недостатки сетей АРТ. Дальнейшие перспективы.
7. КОГНИТРОН И НЕОКОГНИТРОН
Введение в проблему компьютерного распознавания образов. Структура когнитрона. Возбуждающие и тормозящие нейроны. Процедура обучения когнитрона. Достоинства и недостатки когнитрона. Структура и функционирование неокогнитрона.
ЗАКЛЮЧЕНИЕ
Основные функциональные возможности программ моделирования нейронных сетей. Краткий обзор нейропакетов. Краткая характеристика задач, решаемых с помощью нейропакетов: задачи прогнозирования, анализа данных, сжатия и восстановления данных, аппроксимации функций. Основные выводы.
Основная литература
- Хайкин С. Нейронные сети: полный курс. 2-е изд. Москва, 2008.
- Осовский С. Нейронные сети для обработки информации. Москва, 2002.
- Уоссермен Ф. Нейрокомпьютерная техника Москва, 1992.
- Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. Москва, 2002.
- Каллан Р. Основные концепции нейронных сетей. Москва, 2003.
- Николлс Д., Мартин Р., Валлас Б., Фукс П. От нейрона к мозгу. 2-е изд. Москва 2008.
Применение нейронных сетей для задач классификации
Решение задачи классификации является одним из важнейших применений нейронных сетей.
Задача классификации представляет собой задачу отнесения образца к одному из нескольких попарно не пересекающихся множеств. Примером таких задач может быть, например, задача определения кредитоспособности клиента банка, медицинские задачи, в которых необходимо определить, например, исход заболевания, решение задач управления портфелем ценных бумаг (продать купить или «придержать» акции в зависимости от ситуации на рынке), задача определения жизнеспособных и склонных к банкротству фирм.
Цель классификации
При решении задач классификации необходимо отнести имеющиеся статические образцы (характеристики ситуации на рынке, данные медосмотра, информация о клиенте) к определенным классам. Возможно несколько способов представления данных. Наиболее распространенным является способ, при котором образец представляется вектором. Компоненты этого вектора представляют собой различные характеристики образца, которые влияют на принятие решения о том, к какому классу можно отнести данный образец. Например, для медицинских задач в качестве компонентов этого вектора могут быть данные из медицинской карты больного. Таким образом, на основании некоторой информации о примере, необходимо определить, к какому классу его можно отнести. Классификатор таким образом относит объект к одному из классов в соответствии с определенным разбиением N-мерного пространства, которое называется пространством входов, и размерность этого пространства является количеством компонент вектора.
Прежде всего, нужно определить уровень сложности системы. В реальных задачах часто возникает ситуация, когда количество образцов ограничено, что осложняет определение сложности задачи. Возможно выделить три основных уровня сложности. Первый (самый простой) – когда классы можно разделить прямыми линиями (или гиперплоскостями, если пространство входов имеет размерность больше двух) – так называемая линейная разделимость. Во втором случае классы невозможно разделить линиями (плоскостями), но их возможно отделить с помощью более сложного деления – нелинейная разделимость. В третьем случае классы пересекаются и можно говорить только о вероятностной разделимости.
В идеальном варианте после предварительной обработки мы должны получить линейно разделимую задачу, так как после этого значительно упрощается построение классификатора. К сожалению, при решении реальных задач мы имеем ограниченное количество образцов, на основании которых и производится построение классификатора.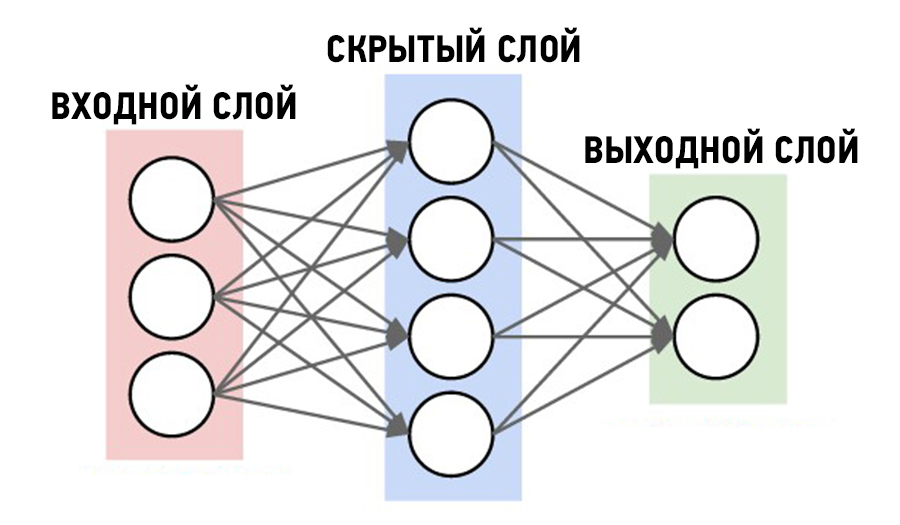 При этом мы не можем провести такую предобработку данных, при которой будет достигнута линейная разделимость образцов.
При этом мы не можем провести такую предобработку данных, при которой будет достигнута линейная разделимость образцов.
Использование нейронных сетей в качестве классификатора
Сети с прямой связью являются универсальным средством аппроксимации функций, что позволяет их использовать в решении задач классификации. Как правило, нейронные сети оказываются наиболее эффективным способом классификации, потому что генерируют фактически большое число регрессионных моделей (которые используются в решении задач классификации статистическими методами).
К сожалению, в применении нейронных сетей в практических задачах возникает ряд проблем. Во-первых, заранее не известно, какой сложности (размера) может потребоваться сеть для достаточно точной реализации отображения. Эта сложность может оказаться чрезмерно высокой, что потребует сложной архитектуры сетей. Так Минский в своей работе «Персептроны» доказал, что простейшие однослойные нейронные сети способны решать только линейно разделимые задачи. Это ограничение преодолимо при использовании многослойных нейронных сетей. В общем виде можно сказать, что в сети с одним скрытым слоем вектор, соответствующий входному образцу, преобразуется скрытым слоем в некоторое новое пространство, которое может иметь другую размерность, а затем гиперплоскости, соответствующие нейронам выходного слоя, разделяют его на классы. Таким образом сеть распознает не только характеристики исходных данных, но и «характеристики характеристик», сформированные скрытым слоем.
Подготовка исходных данных
Для построения классификатора необходимо определить, какие параметры влияют на принятие решения о том, к какому классу принадлежит образец. При этом могут возникнуть две проблемы. Во-первых, если количество параметров мало, то может возникнуть ситуация, при которой один и тот же набор исходных данных соответствует примерам, находящимся в разных классах. Тогда невозможно обучить нейронную сеть, и система не будет корректно работать (невозможно найти минимум, который соответствует такому набору исходных данных).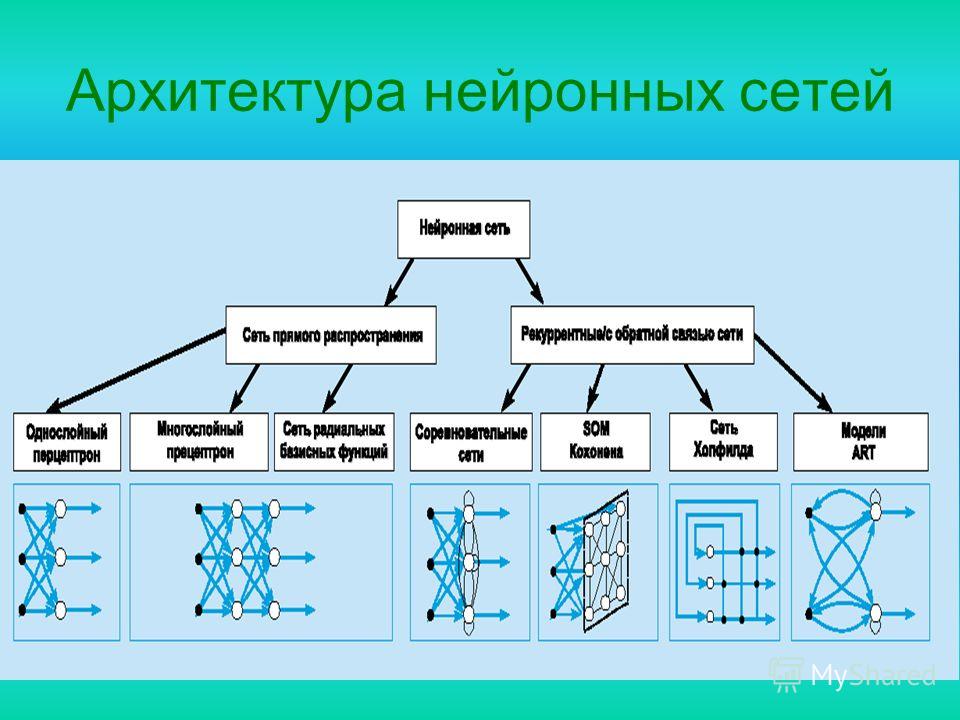 Исходные данные обязательно должны быть непротиворечивы. Для решения этой проблемы необходимо увеличить размерность пространства признаков (количество компонент входного вектора, соответствующего образцу). Но при увеличении размерности пространства признаков может возникнуть ситуация, когда число примеров может стать недостаточным для обучения сети, и она вместо обобщения просто запомнит примеры из обучающей выборки и не сможет корректно функционировать. Таким образом, при определении признаков необходимо найти компромисс с их количеством.
Исходные данные обязательно должны быть непротиворечивы. Для решения этой проблемы необходимо увеличить размерность пространства признаков (количество компонент входного вектора, соответствующего образцу). Но при увеличении размерности пространства признаков может возникнуть ситуация, когда число примеров может стать недостаточным для обучения сети, и она вместо обобщения просто запомнит примеры из обучающей выборки и не сможет корректно функционировать. Таким образом, при определении признаков необходимо найти компромисс с их количеством.
Далее необходимо определить способ представления входных данных для нейронной сети, т.е. определить способ нормирования. Нормировка необходима, поскольку нейронные сети работают с данными, представленными числами в диапазоне 0..1, а исходные данные могут иметь произвольный диапазон или вообще быть нечисловыми данными. При этом возможны различные способы, начиная от простого линейного преобразования в требуемый диапазон и заканчивая многомерным анализом параметров и нелинейной нормировкой в зависимости от влияния параметров друг на друга.
Кодирование выходных значений
Задача классификации при наличии двух классов может быть решена на сети с одним нейроном в выходном слое, который может принимать одно из двух значений 0 или 1, в зависимости от того, к какому классу принадлежит образец. При наличии нескольких классов возникает проблема, связанная с представлением этих данных для выхода сети. Наиболее простым способом представления выходных данных в таком случае является вектор, компоненты которого соответствуют различным номерам классов. При этом i-я компонента вектора соответствует i-му классу. Все остальные компоненты при этом устанавливаются в 0. Тогда, например, второму классу будет соответствовать 1 на 2 выходе сети и 0 на остальных. При интерпретации результата обычно считается, что номер класса определяется номером выхода сети, на котором появилось максимальное значение. Например, если в сети с тремя выходами мы имеем вектор выходных значений (0. n = \frac{k!}{n!\,(k\,-\,n)!} = \frac{k!}{2!\,(k\,-\,2)!} = \frac{k\,(k\,-\,1)}{2}$
n = \frac{k!}{n!\,(k\,-\,n)!} = \frac{k!}{2!\,(k\,-\,2)!} = \frac{k\,(k\,-\,1)}{2}$
Тогда, например, для задачи с четырьмя классами мы имеем 6 выходов (подзадач) распределенных следующим образом:
| N подзадачи(выхода) | КомпонентыВыхода |
|---|---|
| 1 | 1-2 |
| 2 | 1-3 |
| 3 | 1-4 |
| 4 | 2-3 |
| 5 | 2-4 |
| 6 | 3-4 |
Где 1 на выходе говорит о наличии одной из компонент. Тогда мы можем перейти к номеру класса по результату расчета сетью следующим образом: определяем, какие комбинации получили единичное (точнее близкое к единице) значение выхода (т.е. какие подзадачи у нас активировались), и считаем, что номер класса будет тот, который вошел в наибольшее количество активированных подзадач (см. таблицу).
| N класса | Акт. Выходы |
|---|---|
| 1 | 1,2,3 |
| 2 | 1,4,5 |
| 3 | 2,4,6 |
| 4 | 3,5,6 |
Это кодирование во многих задачах дает лучший результат, чем классический способ кодирование.
Выбор объема сети
Правильный выбор объема сети имеет большое значение. Построить небольшую и качественную модель часто бывает просто невозможно, а большая модель будет просто запоминать примеры из обучающей выборки и не производить аппроксимацию, что, естественно, приведет к некорректной работе классификатора. Существуют два основных подхода к построению сети – конструктивный и деструктивный. При первом из них вначале берется сеть минимального размера, и постепенно увеличивают ее до достижения требуемой точности. При этом на каждом шаге ее заново обучают. Также существует так называемый метод каскадной корреляции, при котором после окончания эпохи происходит корректировка архитектуры сети с целью минимизации ошибки. При деструктивном подходе вначале берется сеть завышенного объема, и затем из нее удаляются узлы и связи, мало влияющие на решение. При этом полезно помнить следующее правило: число примеров в обучающем множестве должно быть больше числа настраиваемых весов. Иначе вместо обобщения сеть просто запомнит данные и утратит способность к классификации – результат будет неопределен для примеров, которые не вошли в обучающую выборку.
При этом полезно помнить следующее правило: число примеров в обучающем множестве должно быть больше числа настраиваемых весов. Иначе вместо обобщения сеть просто запомнит данные и утратит способность к классификации – результат будет неопределен для примеров, которые не вошли в обучающую выборку.
Выбор архитектуры сети
При выборе архитектуры сети обычно опробуется несколько конфигураций с различным количеством элементов. При этом основным показателем является объем обучающего множества и обобщающая способность сети. Обычно используется алгоритм обучения Back Propagation (обратного распространения) с подтверждающим множеством.
Алгоритм построения классификатора на основе нейронных сетей
- Работа с данными
- Составить базу данных из примеров, характерных для данной задачи
- Разбить всю совокупность данных на два множества: обучающее и тестовое (возможно разбиение на 3 множества: обучающее, тестовое и подтверждающее).
- Предварительная обработка
- Выбрать систему признаков, характерных для данной задачи, и преобразовать данные соответствующим образом для подачи на вход сети (нормировка, стандартизация и т.д.). В результате желательно получить линейно отделяемое пространство множества образцов.
- Выбрать систему кодирования выходных значений (классическое кодирование, 2 на 2 кодирование и т.д.)
- Конструирование, обучение и оценка качества сети
- Выбрать топологию сети: количество слоев, число нейронов в слоях и т.д.
- Выбрать функцию активации нейронов (например «сигмоида»)
- Выбрать алгоритм обучения сети
- Оценить качество работы сети на основе подтверждающего множества или другому критерию, оптимизировать архитектуру (уменьшение весов, прореживание пространства признаков)
- Остановится на варианте сети, который обеспечивает наилучшую способность к обобщению и оценить качество работы по тестовому множеству
- Использование и диагностика
- Выяснить степень влияния различных факторов на принимаемое решение (эвристический подход).

- Убедится, что сеть дает требуемую точность классификации (число неправильно распознанных примеров мало)
- При необходимости вернутся на этап 2, изменив способ представления образцов или изменив базу данных.
- Практически использовать сеть для решения задачи.
- Выяснить степень влияния различных факторов на принимаемое решение (эвристический подход).
Для того, чтобы построить качественный классификатор, необходимо иметь качественные данные. Никакой из методов построения классификаторов, основанный на нейронных сетях или статистический, никогда не даст классификатор нужного качества, если имеющийся набор примеров не будет достаточно полным и представительным для той задачи, с которой придется работать системе.
НОУ ИНТУИТ | Основы теории нейронных сетей
Форма обучения:
дистанционная
Стоимость самостоятельного обучения:
бесплатно
Доступ:
свободный
Документ об окончании:
Уровень:
Специалист
Длительность:
13:49:00
Выпускников:
1080
Качество курса:
4.37 | 4.06
Одним из популярных направлений Artificial Intelligence является теория нейронных сетей (neuron nets). Данный курс является систематизированным вводным курсом в это направление. Нашей целью является познакомить слушателей с основными нейроно-сетевыми парадигмами, показать область применения этого направления.
Людей всегда интересовало их собственное мышление. Это самовопрошение, думанье мозга о себе самом является, возможно, отличительной чертой человека. Нейробиологи и нейроанатомы достигли в этой области значительного прогресса. Усердно изучая структуру и функции нервной системы человека, они многое поняли в «электропроводке» мозга, но мало узнали о его функционировании. В процессе накопления ими знаний выяснилось, что мозг имеет ошеломляющую сложность. Сотни миллиардов нейронов, каждый из которых соединен с сотнями или тысячами других, образуют систему, далеко превосходящую наши самые смелые мечты о суперкомпьютерах. На сегодняшний день существуют две взаимно обогащающие друг друга цели нейронного моделирования: первая – понять функционирование нервной системы человека на уровне физиологии и психологии и вторая – создать вычислительные системы (искусственные нейронные сети), выполняющие функции, сходные с функциями мозга. Именно эта последняя цель и находится в центре внимания данного курса.
На сегодняшний день существуют две взаимно обогащающие друг друга цели нейронного моделирования: первая – понять функционирование нервной системы человека на уровне физиологии и психологии и вторая – создать вычислительные системы (искусственные нейронные сети), выполняющие функции, сходные с функциями мозга. Именно эта последняя цель и находится в центре внимания данного курса.
В лекциях курса рассматриваются такие классические нейроно-сетевые парадигмы как персептроны, сети Хопфилда и Хэмминга, сети встречного распространения, двунаправленная ассоциативная память, теория адаптивного резонанса, когнитроны и неокогнитроны. Для каждой рассматриваемой сети дается описание ее архитектуры, алгоритмов обучения, анализируются проблемы емкости и устойчивости сети.
ISBN: 978-5-9556-0049-9
Теги: .net, алгоритмы, АРТ, выходной слой, искусственная жизнь, искусственные нейронные сети, исследования, когнитрон, компоненты, локальные минимумы, нейронные сети, обучение, персептрон, поиск, процедуры, сеть хопфилда, синапс, сходимость, фотографии, целевая функция
Предварительные курсы
Дополнительные курсы
2 часа 30 минут
—
Основы искусственных нейронных сетей
В лекции рассматриваются общие положения теории искусственных нейронных сетей. Описана структура однослойных и многослойных нейронных сетей, введено понятие обучения нейронной сети и дана классификация алгоритмов обучения.
—
Персептроны. Представимость и разделимость
В лекции дается определение персептрона, рассматривается его архитектура.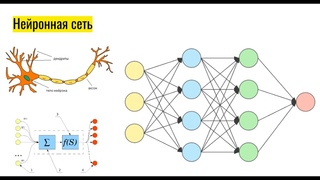 Описывается класс задач, решаемых с помощью персептрона, доказывается, какие задачи невозможно решить с его помощью.
Описывается класс задач, решаемых с помощью персептрона, доказывается, какие задачи невозможно решить с его помощью.
—
Персептроны. Обучение персептрона
В лекции рассматриваются алгоритм обучения персептрона, вопросы сходимости алгоритма обучения и подбора количественных характеристик весовых коэффициентов. Исследуются многослойные персептроны и возможности их обучения.
—
Сети встречного распространения
В лекции изложены архитектура, функционирование и методы обучения сетей встречного распространения. В качестве примера использования данной сети рассматриваются методы сжатия данных.
—
Стохастические методы обучения нейронных сетей
В лекции дается обзор основных стохастических методов, используемых для обучения нейронных сетей: метод отжига металла, больцмановское обучение, обучение Коши, метод искусственной теплоемкости.
—
Нейронные сети Хопфилда и Хэмминга
В лекции рассматривается архитектура сети Хопфилда и ее модификация — сеть Хэмминга, затрагиваются вопросы устойчивости сети Хопфилда. В заключении лекции рассматриваются понятие ассоциативности памяти и задача распознавания образов.
—
Обобщения и применения модели Хопфилда
В лекции рассматриваются вероятностные обобщения модели Хопфилда и статистическая машина. Описывается аналого-цифровой преобразователь — как модель сети с обратным распределением. В качестве примера приводится представление информации в сети Хопфилда, решающей задачу коммивояжера.
В качестве примера приводится представление информации в сети Хопфилда, решающей задачу коммивояжера.
—
Двунаправленная ассоциативная память
В лекции рассматриваются архитектура и принципы работы нейронной сети ДАП. Затронуты вопросы емкости данной сети. Дается обзор некоторых модификаций этой сети.
—
Теория адаптивного резонанса. Реализация
В лекции рассматривается процесс функционирования АРТ. Приводится пример обучения сети АРТ. Обсуждаются основные характеристики АРТ. Дается обзор модификаций сети АРТ.
—
Когнитрон
В лекции рассматривается архитектура, процедура обучения и функционирование когнитрона. Описан пример функционирования четырехслойного когнитрона распознавания образов.
—
Неокогнитрон
В лекции рассматривается архитектура, процедура обучения и функционирования неокогнитрона. Отмечается его сходство и отличие от когнитрона.
—
Алгоритмы обучения
В данной лекции рассматриваются различные методы обучения нейронных сетей. Некоторые из этих методов частично приводились на предыдущих лекциях, но отмечены снова для создания у слушателей целостного представления об изучаемой области.
—
Страница 1 из 4 Сеть, в которой все входные элементы соединены непосредственно с выходными элементами, называется однослойной нейронной сетью, или сетью персептрона. Начнем с исследования пространства гипотез, которое может быть представлено с помощью персептрона. Если применяется пороговая функция активации, то пер-септрон может рассматриваться как представляющий некоторую булеву функцию. Кроме элементарных булевых функций AND, OR и NOT (см. рис. 20.17), персептрон позволяет представлять очень компактно некоторые весьма «сложные» булевы функции. Например, мажоритарная функция, которая выводит 1, только если 1 присутствует больше чем на половине из ее n входов, может быть представлена с помощью персептрона, в котором каждое значение, а пороговое значение В дереве решений для представления этой функции потребовалось быузлов. Рис. 20.19. Свойства сети персептрона: сеть персептрона, состоящая из трех выходных элементов персептрона, в которых совместно используются пять входных элементов (а). Рассматривая конкретный выходной элемент (скажем, второй элемент, выделенный жирным контуром), можно обнаружить, что веса его входных связей не влияют на другие выходные элементы; графическое изображение выходных данных элемента персептрона с двумя входами, имеющего сигмоидалъную функцию активации (б) К сожалению, существует также много булевых функций, которые не могут быть представлены с помощью порогового персептрона. Рассматривая уравнение 20.10, можно обнаружить, что пороговый персептрон возвращает 1 тогда и только тогда, когда взвешенная сумма его входных данных (включая смещение) является положительной: |
Нейронные сети
Нейросеть для диагностики COVID-19
В Москве силами отечественных специалистов была разработана нейросеть для оценки степени поражения легких при коронавирусе COVID-19. Об этом сообщил мэр Москвы Сергей Собянин в своем личном блоге.
Об этом сообщил мэр Москвы Сергей Собянин в своем личном блоге.
Проект получил название «КТ-калькулятор», и его интерфейс действительно напоминает калькулятор, только со значительно большим количеством полей ввода. Для получения результата нужно указать пол, возраст пациента, ответить на вопросы об имеющихся симптомах и привести результаты анализа крови.
В разработке нейросети участвовали, в том числе, сотрудники МГУ им. Ломоносова. В ее основе лежат технологии искусственного интеллекта (ИИ) и машинного обучения, и на первых этапах обучения в нейросеть выгружали медкарты пациентов, вылеченных от коронавируса в Москве в период с весны 2020 г.
В общей сложности разработчики выгрузили в нейросеть свыше 500 тыс. историй болезни пациентов. О том, предоставили ли эти пациенты разработчикам право использовать данные из их медкарт, на сайте Сергея Собянина не сказано.
Полный текст читайте здесь «В России создана нейросеть для диагностики COVID-19» >>>
Международная группа ученых под руководством специалистов из Политехнического института Ренсселера разработала нейросеть, способную предсказать необходимость интенсивной терапии у больных с вызванной COVID-19 пневмонией в 96% случаев. Исследование еще не рецензировалось, предварительные данные были опубликованы в журнале Medical Image Analysis.
Хотя у большинства пациентов COVID-19 протекает в сравнительно легкой форме, некоторые сталкиваются с тяжелой пневмонией, которая приводит к острой дыхательной недостаточности и требует подключения к аппарату ИВЛ. Но количество мест в отделениях интенсивной терапии ограничено, и, по мере увеличения числа зараженных, врачам приходится выбирать, кому из тяжелобольных пациентов помощь окажется нужнее.
Те, у кого развивается наиболее тяжелая форма COVID-19, имеют ряд общих черт, и машина может найти их быстрее человека, отмечают ученые.
кейс от NAUKA — Наука
Обилие рабочих задач не мешает увлечённым профессионалам стремиться к развитию.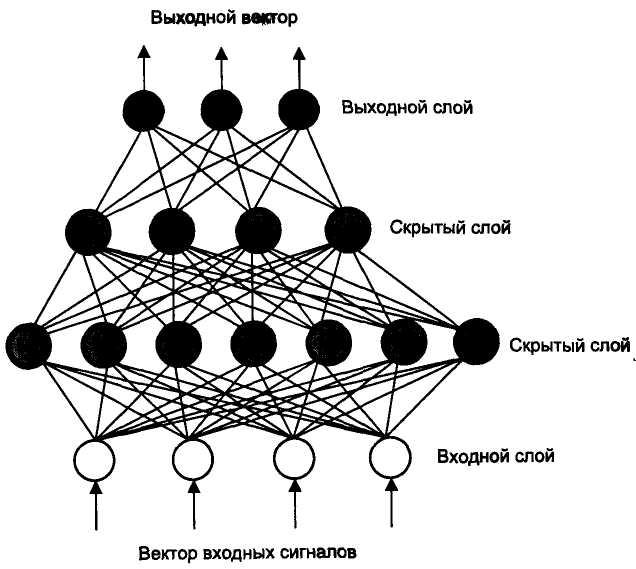 Создание корпоративного проекта NaukaLabs – тому подтверждение. Наши исследования будут направлены на выявление идей с высоким потенциалом для бизнеса и освоение прогрессивных технологий. Первой ласточкой стала нейронная сеть.
Создание корпоративного проекта NaukaLabs – тому подтверждение. Наши исследования будут направлены на выявление идей с высоким потенциалом для бизнеса и освоение прогрессивных технологий. Первой ласточкой стала нейронная сеть.
Теория
Материалов по нейросетям слишком много, чтобы углубляться в объяснение технологии без повтора всем известных фактов. Поэтому расскажем о ней буквально в двух словах.
Структура нейронной сети пришла в мир программирования из биологии:
В мозге человека находятся миллионы нейронов, передающих информацию в виде импульсов. Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами, которые могут усиливать или ослаблять проходящий по ним электрический сигнал. Это ключевой момент, используемый в концепции искусственных нейронных сетей: по принципу функционирования биологических нейронных сетей – нервных клеток живого организма – и строится математическая модель. Реализация искусственной нейросети в виде программы обретает способность анализировать и даже запоминать информацию.
Для изучения процессов, протекающих в мозге, и при попытке их моделирования возникло понятие искусственного нейрона. Роль синапсов играют весовые коэффициенты, корректирующие значение входящих в нейрон данных. Сравнение суммы всех взвешенных сигналов со значением функции активации даёт на выходе тот или иной результат.
Искусственный нейрон
Совокупности нейронов могут образовывать нейронные сети, содержащие один или несколько слоёв. Картинка ниже – для самого простого случая: кружками обозначен входной слой, который не считается слоем нейронной сети, а справа расположен слой обычных нейронов. В однослойных нейронных сетях сигналы с входного слоя сразу подаются на выходной слой. Он производит необходимые вычисления, результаты которых сразу подаются на выходы.
Однослойная нейронная сеть
Более сложная структура – многослойная нейросеть. Работу скрытых слоев нейронов можно сравнить с крупным производством. Продукт – выходной сигнал – на заводе собирается по стадиям. После каждого станка получается некий промежуточный результат. Скрытые слои таким же образом превращают входные сигналы в те или иные промежуточные результаты.
Продукт – выходной сигнал – на заводе собирается по стадиям. После каждого станка получается некий промежуточный результат. Скрытые слои таким же образом превращают входные сигналы в те или иные промежуточные результаты.
Многослойная нейронная сеть
Особый интерес представляют сети с обратными связями. С помощью рекуррентных сетей можно восстанавливать или дополнять сигналы. Другими словами, такие нейросети имеют свойства кратковременной памяти, как у человека.
Рекуррентная нейронная сеть
Для каких целей полезна нейросеть? Перечислим основные типы задач:
- Классификация. Технология сильно упрощает распределение данных по параметрам. Например, на вход даётся набор людей, и нужно решить, кому из них давать кредит, а кому нет. Эту работу может эффективно проделать нейронная сеть, анализируя возраст, платежеспособность, кредитную историю и т.д.
- Регрессионный анализ. В переводе на русский, аппроксимация и прогнозирование. В качестве примера приведём возможность предсказывать следующий рост или падение акций, основываясь на текущей ситуации на фондовом рынке.
- Кластеризация. Эта цель очень схожа с классификацией, правда, её результатом является кластер – по сути целый класс. Другими словами, кластеризация – это классификация, выполняемая самой нейронной сетью: нельзя определить заранее, какие получатся классы. Зато можно выявить скрытые или незамеченные зависимости между изучаемыми объектами нейронной сети
Прежде чем использовать нейросеть, её необходимо обучить. Этот процесс сводится к поиску такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной. Существуют два основных способа:
- Обучение с учителем — веса меняются так, чтобы ответы сети минимально отличались от уже готовых правильных ответов.
- Обучение без учителя — сеть самостоятельно классифицирует входные сигналы.
 Правильные (эталонные) выходные сигналы при этом не демонстрируются.
Правильные (эталонные) выходные сигналы при этом не демонстрируются.
Практика
Только за последние полгода в службу поддержки компании NAUKA пользователи направили около 5700 сообщений. Сортировать их вручную слишком долго и скучно, куда веселее создать нейросеть, классифицирующую письма по типам.
Перечислим основные причины обращения:
- Ошибка. Сообщение описывает сбой программного обеспечения.
- Новые требования (пожелания). Обращение связано с новыми требованиями к функционалу ПО или пожеланиями к изменению данных.
- Требуется обучение (консультация). Пользователь сталкивается с незнанием работы программы или бизнес-процесса.
- Причина не поддаётся определению. Сообщения не имеют отношения к ПО – например, поздравления с 8 марта, Новым годом, просто ошибочные письма и т.д.
Разделим задачу создания нейросети на этапы решения:
- построить нейронную сеть, классифицирующую на основе текста сообщения;
- создать нейросеть, классифицирующую на основе ошибки в логе;
- написать нейронную сеть для обработки картинки, чтобы определить, содержит ли изображение окно с ошибкой;
- сочетать полученные нейронные сети, используя их вместе, или на их основе построить обобщенную сеть.
На момент написания статьи NAUKA воплотила в жизнь первый шаг – сортировку на основе текста. Эта задача также выполнялась поэтапно:
- создание словаря,
- подбор модели нейронной сети,
- обучение сети,
- проверка сети – определение процента правильных ответов.
Остановимся подробнее на каждой стадии.
Создание словаря нейросети
Словарь – это весь массив имеющих смысловую нагрузку слов, что содержатся в выборке обучаемой модели. Не каждое слово, встреченное в тексте, является значимым, поэтому массив необходимо обработать.
Предлоги, междометия и слова из чёрного списка («здравствуйте», «спасибо» и др.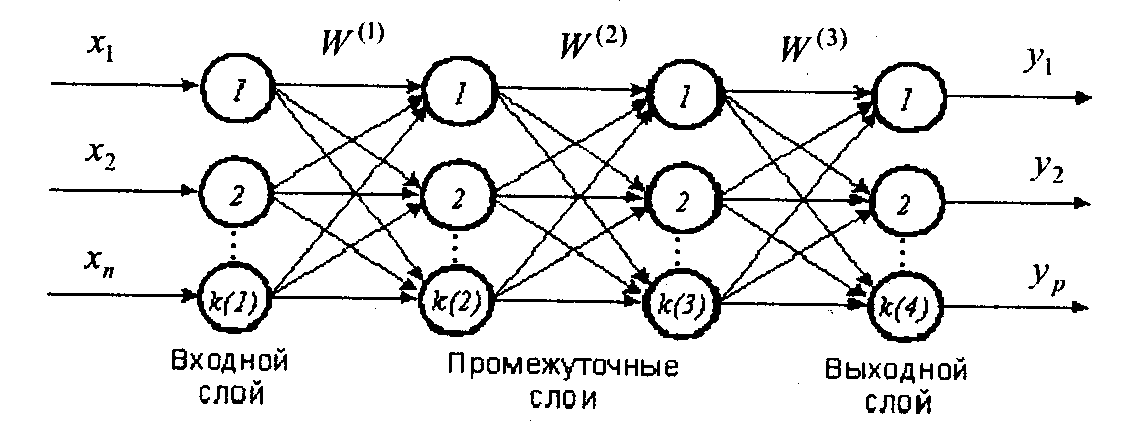 ) следует исключить из словаря. Также необходимо удалить слова, содержащие цифры, а прочие слова – нормализовать. В этом нам помог Стеммер Портера – алгоритм, позволяющий отсечь окончания и суффиксы, основываясь на особенностях языка. Слова, встреченные менее чем в четырёх сообщениях, исключаем, а каждому оставшемуся слову ставим в соответствие номер входной переменной.
) следует исключить из словаря. Также необходимо удалить слова, содержащие цифры, а прочие слова – нормализовать. В этом нам помог Стеммер Портера – алгоритм, позволяющий отсечь окончания и суффиксы, основываясь на особенностях языка. Слова, встреченные менее чем в четырёх сообщениях, исключаем, а каждому оставшемуся слову ставим в соответствие номер входной переменной.
В результате получилось 1111 значимых слов. Однако нейронная сеть не умеет работать непосредственно со словами, поэтому текст сообщения необходимо превратить в массив числовых значений.
На входе текст сообщения разбиваем на слова, нормализуем и проверяем его наличие в словаре. Если слово присутствует, переменной с соответствующим номером присваиваем значение 1. На выходе получаем массив длиной 1111 элементов, состоящий из нулей и единиц:
(1, 0, 0, 1, … , 0, 1, 0)
Построение нейронной сети
Делать с нуля слишком долго, так что мы решили использовать библиотеку Encog 3.3 – бесплатный API-интерфейс нейронной сети с открытым исходным кодом для Java и .Net. Используем сеть прямого распространения, т.е. от входа к выходу. Не хочется грузить читателей математикой, поэтому лишь упомянем для тех, кому это важно, что в качестве функции активации была выбрала сигмоидальная функция.
Специалисты NAUKA исследовали 3 варианта нейросети – с двумя скрытыми слоями нейронов, с одним скрытым слоем и без скрытых слоёв.
Обучение нейронной сети
Как было указано выше, в качестве тестовой выборки мы использовали 3416 сообщений, присланных в службу поддержки NAUKA за последние полгода. 75% этих данных мы направили на обучение нейросети, остальные 25% оставили для проверки.
Выполняем обучение с уровнем допустимой ошибки в 1%, используя алгоритм обучения Resilient Propagation (RProp). В отличие от других алгоритмов, также основанных на методе градиентного спуска, RProp использует знаки частных производных, а не их значения.
Проверка показала, что из поданных в обученную сеть сообщений верно классифицированы только 55%. Возможно ли улучшить этот показатель?
Переобучение
Переобучение – явление, когда построенная модель хорошо объясняет примеры из обучающей выборки, но относительно плохо работает на примерах, не участвовавших в обучении. При минимальной ошибке в процессе обучения сети она становится менее вариативной к данным, не участвующим в обучении.
Обучаем нейронную сеть до ошибки в 8% (в реальности оказалось максимум 7,2%). Проверка дала более удачный результат в 65% сообщений, классифицированных корректно. На этом этапе было замечено, что на одни и те же модули идут преимущественно сообщения одного содержания. Расширяем словарь, добавив сигнатуры модулей. Результат составил 68,6%.
Стоит отметить, что и многослойные, и однослойные нейросети дали одинаковый результат при проверке. Это говорит о линейной разделимости множества исходных данных. Значит, на практике допустимо использовать нейронную сеть без скрытых слоёв.
И всё же – можно ли улучшить прогноз? Можно, если учесть скрытые зависимости, которые не удалось отследить нашим программистам. А с этой задачей хорошо справится сама нейросеть, решающая задачу кластеризации. Для этого попробуем отойти от сетей прямого распространения. На сей раз используем нейронную сеть Кохонена – этот класс сетей, как правило, обучается без учителя и успешно применяется в задачах распознавания.
Выбрав алгоритм обучения Neighborhood Competitive Training, мы исследовали сети с числом кластеров, равным 10, 20, 40, 60, 80, 100. Остановились на 80 кластерах – проверка показала точность прогноза, равную 64,98%. Таким образом, кластеризация дала результаты, схожие с обучающей выборкой.
Выводы
Текста сообщения недостаточно, чтобы уверенно прогнозировать его тип. Прогноз может быть неточным из-за того, что сообщения с идентичным текстом могут относиться к разным темам. Следовательно, проекту NaukaLabs есть куда развиваться – нас ждут задачи создания нейросети, классифицирующей на основе ошибки в логе, нейронной сети, анализирующей картинку, и сочетания этих технологий.
Перспективы применения таких программ весьма обширны – даже в рамках лишь одного из наших проектов. К примеру, нейросеть может рассматривать любые тексты от пользователей сайта на предмет запрещённых материалов – продажи сомнительных препаратов, нецензурной лексики, экстремизма и т.п. Она способна помочь службе поддержки в формировании возможных ответов на обращения. Технология упростит поиск людей по фото и анализ изображений для выявления порнографии. И это лишь малая толика возможностей нейронных сетей. Будем пробовать их на себе и обязательно поделимся новыми кейсами с вами!
NAUKA ВКонтакте
NAUKA в Facebook
NAUKA в Instagram
Вернуться в пресс-центр
Введение в искусственные нейронные сети (ANN)
Дата публикации Oct 3, 2019
Источник:getwallpapers.com
Deep Learning — самая захватывающая и мощная ветвь машинного обучения. Это техника, которая учит компьютеры делать то, что естественно для человека: учиться на примере. Глубокое обучение — ключевая технология автомобилей без водителя, позволяющая им распознавать знак остановки или отличать пешехода от фонарного столба. Это ключ к голосовому управлению в потребительских устройствах, таких как телефоны, планшеты, телевизоры и громкоговорители громкой связи. Глубокое обучение привлекает много внимания в последнее время и по уважительной причине. Это достижение результатов, которые раньше были невозможны.
При глубоком обучении компьютерная модель учится выполнять классификационные задачи непосредственно из изображений, текста или звука. Модели глубокого обучения могут достигать современной точности, иногда превышая производительность на уровне человека. Модели обучаются с использованием большого набора помеченных данных и архитектур нейронных сетей, которые содержат много слоев.
Источник
Модели глубокого обучения могут использоваться для различных сложных задач:
- Искусственные нейронные сети (ANN) для регрессии и классификации
- Сверточные нейронные сети (CNN) для компьютерного зрения
- Рекуррентные нейронные сети (RNN) для анализа временных рядов
- Самоорганизующиеся карты для извлечения объектов
- Машины Deep Boltzmann для систем Рекомендации
- Авто Энкодеры для систем Рекомендации
В этой статье мы постараемся охватить все, что связано с искусственными нейронными сетями или ANN.
«Искусственные нейронные сети или ИНС — это парадигма обработки информации, которая вдохновлена тем, как биологическая нервная система, такая как мозг, обрабатывает информацию. Он состоит из большого количества сильно взаимосвязанных процессорных элементов (нейронов), работающих в унисон для решения конкретной проблемы ».
Темы для покрытия:
- Нейроны
- Функции активации
- Типы функций активации
- Как работают нейронные сети
- Как учатся нейронные сети (обратное распространение)
- Градиентный спуск
- Стохастический градиентный спуск
- Тренинг АНН со стохастическим градиентным спуском
Биологические нейроны (также называемые нервными клетками) или просто нейроны являются фундаментальными единицами головного мозга и нервной системы, клетки, ответственные за получение сенсорного ввода из внешнего мира через дендриты, обрабатывают его и выдают выход через аксоны.
Биологический Нейрон
Клеточное тело (сома):Тело нейронной клетки содержит ядро и осуществляет биохимическое преобразование, необходимое для жизни нейронов.
Дендриты:Каждый нейрон имеет тонкие, похожие на волосы трубчатые структуры (удлинения) вокруг него. Они разветвляются на дерево вокруг тела клетки. Они принимают входящие сигналы.
Axon:Это длинная тонкая трубчатая структура, которая работает как линия электропередачи.
Synapse:Нейроны связаны друг с другом в сложном пространственном расположении. Когда аксон достигает своего конечного пункта назначения, он снова разветвляется, что называется окончательной обработкой деревьев В конце аксона очень сложные и специализированные структуры, называемые синапсами. Связь между двумя нейронами происходит в этих синапсах.
Дендриты получают вход через синапсы других нейронов. Сома обрабатывает эти входящие сигналы с течением времени и преобразует это обработанное значение в выходной сигнал, который отправляется другим нейронам через аксон и синапсы.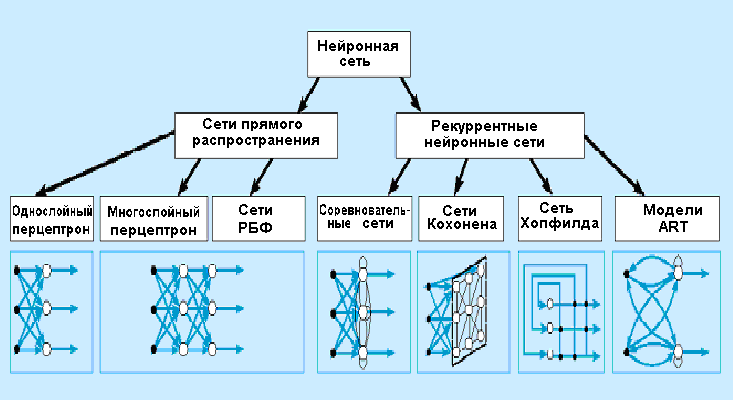
Поток электрических сигналов через нейроны.
Следующая диаграмма представляет общую модель ANN, которая вдохновлена биологическим нейроном. Это также называется Perceptron.
Однослойная нейронная сеть называется персептроном. Это дает один выход.
Perceptron
На рисунке выше, для одного наблюдения,x0, x1, x2, x3...x(n)представляет различные входы (независимые переменные) в сеть. Каждый из этих входов умножается на вес соединения или синапс. Веса представлены в видеw0, w1, w2, w3….w(n),Вес показывает силу конкретного узла.
b является величиной смещения. Значение смещения позволяет сместить функцию активации вверх или вниз.
В простейшем случае эти произведения суммируются, подаются в передаточную функцию (функцию активации) для генерации результата, и этот результат отправляется как выходной.
Математически, x1.w1 + x2.w2 + x3.w3 ...... xn.wn = ∑ xi.wi
Теперь функция активации применяется𝜙(∑ xi.wi)
Функция активации важна для ИНС, чтобы учиться и понимать что-то действительно сложное. Их основная цель — преобразовать входной сигнал узла в ANN в выходной сигнал. Этот выходной сигнал используется как вход для следующего слоя в стеке.
Функция активации решает, следует ли активировать нейрон, вычисляя взвешенную сумму и дополнительно добавляя к ней смещение. Мотив состоит в том, чтобы ввести нелинейность в выход нейрона.
Если мы не применяем функцию активации, то выходной сигнал будет просто линейной функцией (полинома в один градус) Теперь линейные функции легко решить, но они ограничены по своей сложности, имеют меньшую мощность. Без функции активации наша модель не может изучать и моделировать сложные данные, такие как изображения, видео, аудио, речь и т. Д.
Теперь возникает вопрос: зачем нам нелинейность?
Нелинейные функции — это те, которые имеют степень больше единицы и имеют кривизну. Теперь нам нужна нейронная сеть для изучения и представления почти всего и любой произвольной сложной функции, которая отображает входные данные в выходные.
Теперь нам нужна нейронная сеть для изучения и представления почти всего и любой произвольной сложной функции, которая отображает входные данные в выходные.
Нейронная сеть считается«Универсальные функциональные аппроксиматоры».Это означает, что они могут изучать и вычислять любую функцию вообще.
Типы функций активации:
1. Активация пороговой функции — (Двоичная пошаговая функция)
Бинарная функция шага является функцией активации на основе порога. Если входное значение выше или ниже определенного порога, нейрон активируется и отправляет точно такой же сигнал на следующий слой.
Двоичная функция шага
Функция активации A = «активирована», если Y> порог
иначе нет или A = 1, если y> порог 0 в противном случае.
Проблема с этой функцией заключается в создании двоичного классификатора (1 или 0), но если вы хотите, чтобы несколько таких нейронов были подключены, чтобы получить больше классов, Class1, Class2, Class3 и т. Д. В этом случае все нейроны будут давать 1 поэтому мы не можем решить.
2. Функция активации сигмовидной кишки — (Логистическая функция)
Сигмовидная функция — это математическая функция, имеющая характерную S-образную кривую или сигмовидную кривую, которая находится в диапазоне от 0 до 1, поэтому она используется для моделей, в которых нам нужно прогнозировать вероятность в качестве выходных данных.
Сигмовидная кривая
Функция сигмоида дифференцируема, это означает, что мы можем найти наклон кривой в любых 2 точках.
Недостаток функции активации Sigmoid состоит в том, что она может вызвать застревание нейронной сети во время тренировки, если будет предоставлен сильный отрицательный вклад.
3. Гиперболическая касательная функция — (tanh)
Это похоже на Sigmoid, но лучше по производительности. Он нелинейный по своей природе, поэтому мы можем сложить слои. Функция находится в диапазоне (-1,1).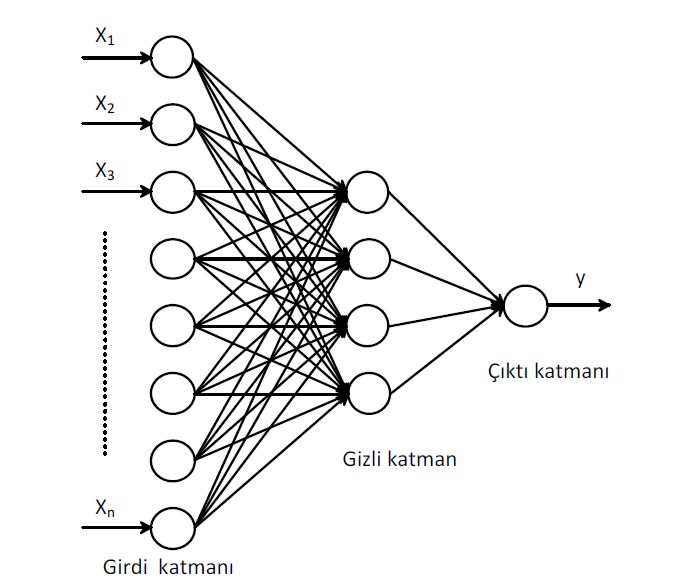
Гиперболическая касательная функция
Основным преимуществом этой функции является то, что сильные отрицательные входные данные будут отображаться на отрицательный выходной сигнал, а только нулевые входные значения сопоставляются с почти нулевыми выходными значениями. Таким образом, меньше вероятности застрять во время обучения.
4. Выпрямленные линейные единицы — (ReLu)
ReLu — наиболее часто используемая функция активации в CNN и ANN, которая находится в диапазоне от нуля до бесконечности. [0, ∞)
РЕЛУ
Он дает вывод «х», если х положительный и 0 в противном случае. Похоже, что имеет ту же проблему линейной функции, что и линейная на положительной оси. Relu является нелинейным по своей природе, и комбинация ReLu также является нелинейной. На самом деле, это хороший аппроксиматор, и любая функция может быть аппроксимирована комбинацией Relu.
ReLu улучшен в 6 раз по сравнению с гиперболической функцией тангенса.
Его следует применять только к скрытым слоям нейронной сети. Таким образом, для выходного слоя используйте функцию softmax для задачи классификации, а для задачи регрессии — линейную функцию.
Здесь одна проблема — некоторые градиенты хрупки во время тренировки и могут умереть. Это вызывает обновление веса, которое никогда не активирует ни одну точку данных. В основном ReLu может привести к мертвым нейронам.
Чтобы решить проблему умирания нейронов,Leaky ReLuбыл представлен. Итак, Leaky ReLu вводит небольшой уклон, чтобы поддерживать обновления. Leaky ReLu находится в диапазоне от -∞ до + ∞.
ReLu vs Leaky ReLu
Утечка помогает увеличить диапазон функции ReLu. Обычно значение а = 0,01 или около того.
Когда а не 0,01, то это называется рандомизированным ReLu.
Давайте возьмем пример цены на недвижимость и для начала у нас есть различные факторы, собранные в один ряд данных:Area, Bedrooms, Distance to city and Age.
Входные значения проходят через взвешенные синапсы прямо на выходной слой. Все четыре будут проанализированы, будет применена функция активации, и результаты будут получены.
Все четыре будут проанализированы, будет применена функция активации, и результаты будут получены.
Это достаточно просто, но есть способ усилить мощь нейронной сети и повысить ее точность путем добавления скрытого слоя, который расположен между входным и выходным слоями.
Нейронная сеть со скрытым слоем (только с ненулевыми значениями)
Теперь на рисунке выше все 4 переменные связаны с нейронами через синапс. Однако не все синапсы взвешены. у них будет либо значение 0, либо не значение 0.
здесь значение, отличное от 0 → указывает на важность
0 значение → Они будут отброшены.
Давайте возьмем примерAreaа такжеDistance to Cityненулевые для первого нейрона, что означает, что они взвешены и имеют значение для первого нейрона. Две другие переменные,Bedroomsа такжеAgeне взвешены и поэтому не учитываются первым нейроном.
Вы можете задаться вопросом, почему этот первый нейрон рассматривает только две из четырех переменных В этом случае на рынке недвижимости принято, что большие дома дешевеют по мере удаления от города. Это основной факт. Так что этот нейрон может искать именно свойства, которые большие, но не так далеко от города.
Теперь, отсюда и сила нейронных сетей. Существует много таких нейронов, каждый из которых выполняет аналогичные вычисления с различными комбинациями этих переменных.
Как только этот критерий будет соблюден, нейрон применяет функцию активации и выполняет свои вычисления. Следующий нейрон вниз мог иметь взвешенные синапсыDistance to the cityа также,Bedrooms,
Таким образом, нейроны работают и взаимодействуют очень гибким способом, позволяя ему искать конкретные вещи и, следовательно, осуществлять всесторонний поиск того, для чего он обучен.
Рассмотрение аналогии может оказаться полезным для понимания механизмов нейронной сети. Обучение в нейронной сети тесно связано с тем, как мы учимся в нашей обычной жизни и деятельности — мы выполняем действие, и тренеры или тренеры принимают его или исправляют, чтобы понять, как лучше справляться с определенной задачей.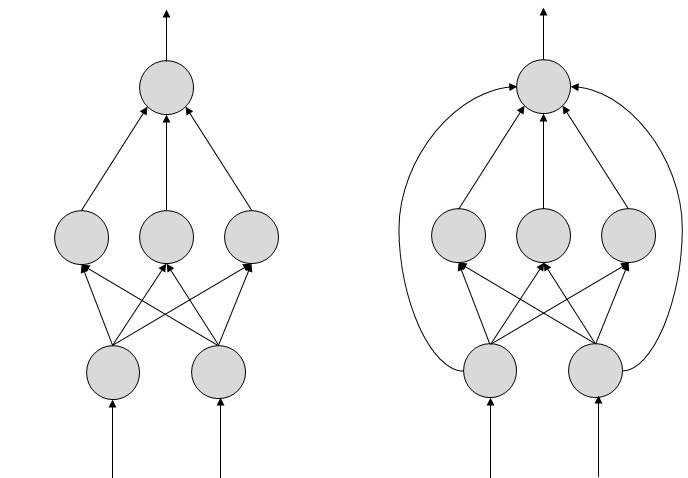 Точно так же нейронные сети требуют тренера, чтобы описать то, что должно было быть произведено как ответ на вход. На основании разницы между фактическим значением и прогнозируемым значением, значение ошибки также называетсяФункция стоимостивычисляется и отправляется обратно через систему.
Точно так же нейронные сети требуют тренера, чтобы описать то, что должно было быть произведено как ответ на вход. На основании разницы между фактическим значением и прогнозируемым значением, значение ошибки также называетсяФункция стоимостивычисляется и отправляется обратно через систему.
Функция стоимости: половина квадрата разницы между фактическим и выходным значением.
Для каждого слоя сети функция стоимости анализируется и используется для настройки порога и весов для следующего ввода. Наша цель — минимизировать функцию затрат. Чем ниже функция стоимости, тем ближе фактическое значение к прогнозируемому значению. Таким образом, ошибка становится незначительно меньше при каждом запуске, так как сеть учится анализировать значения.
Мы передаем полученные данные обратно через всю нейронную сеть. Взвешенные синапсы, соединяющие входные переменные с нейроном, — единственное, что мы можем контролировать.
Пока существует несоответствие между фактическим значением и прогнозируемым значением, мы должны корректировать эти значения. Как только мы немного настроим их и снова запустим нейронную сеть, появится новая функция Cost, которая, будем надеяться, будет меньше, чем предыдущая.
Нам нужно повторять этот процесс, пока мы не уменьшим функцию стоимости до как можно меньшего.
Процедура, описанная выше, известна какОбратное распространениеи применяется непрерывно через сеть, пока значение ошибки не будет минимальным.
Обратное распространение в действии
Есть в основном 2 способа регулировки веса:
1. Метод грубой силы
2. Пакетно-градиентный спуск
Метод грубой силы
Лучше всего подходит для однослойной сети с прямой связью. Здесь вы берете несколько возможных весов. В этом методе мы хотим исключить все другие веса, кроме одного справа внизу U-образной кривой.
Оптимальный вес можно найти с помощью простых методов устранения. Этот процесс устранения работы, если у вас есть один вес для оптимизации. Что делать, если у вас сложный NN с большим количеством весов, этот метод не работает из-заПроклятие размерности.
Этот процесс устранения работы, если у вас есть один вес для оптимизации. Что делать, если у вас сложный NN с большим количеством весов, этот метод не работает из-заПроклятие размерности.
Альтернативный подход, который у нас есть, называется Batch Gradient Descent.
Это алгоритм итеративной оптимизации первого порядка, и его обязанностью является поиск минимальной стоимости (потерь) в процессе обучения модели с различными весами или обновления весов.
Градиентный спуск
В Gradient Descent вместо того, чтобы проходить каждый вес по одному и отмечать каждый неправильный вес по ходу дела, мы вместо этого смотрим на угол функциональной линии.
Если наклон → отрицательный, это означает, что вы идете вниз по кривой.
Если наклон → Положительный, ничего не делать
Таким образом, устраняется огромное количество неправильных весов. Например, если у нас есть 3 миллиона образцов, мы должны пройти через 3 миллиона раз. Так что в основном вам нужно рассчитать каждую стоимость в 3 миллиона раз.
Градиентный спуск работает хорошо, когда у нас выпуклая кривая, как на рисунке выше. Но если у нас нет выпуклой кривой, градиентный спуск не удастся.
Слово ‘стохастический‘Означает систему или процесс, связанный со случайной вероятностью. Следовательно, в Stochastic Gradient Descent несколько выборок выбираются случайным образом вместо всего набора данных для каждой итерации.
Стохастический градиентный спуск
В SGD мы берем один ряд данных за раз, пропускаем их через нейронную сеть, затем корректируем веса. Для второй строки мы запускаем ее, затем сравниваем функцию Cost и затем снова корректируем веса. И так далее…
SGD помогает нам избежать проблемы локальных минимумов. Это намного быстрее, чем Gradient Descent, потому что он запускает каждую строку за раз, и ему не нужно загружать все данные в память для выполнения вычислений.
Следует отметить, что, поскольку SGD, как правило, более шумный, чем типичный градиентный спуск, обычно требуется большее количество итераций для достижения минимумов из-за его случайности при спуске. Несмотря на то, что для достижения минимумов требуется большее количество итераций, чем для обычного градиентного спуска, в вычислительном отношении это все же значительно дешевле, чем для обычного градиентного спуска. Следовательно, в большинстве сценариев SGD предпочтительнее, чем Batch Gradient Descent для оптимизации алгоритма обучения.
Несмотря на то, что для достижения минимумов требуется большее количество итераций, чем для обычного градиентного спуска, в вычислительном отношении это все же значительно дешевле, чем для обычного градиентного спуска. Следовательно, в большинстве сценариев SGD предпочтительнее, чем Batch Gradient Descent для оптимизации алгоритма обучения.
Шаг-1 → Произвольно инициализировать веса для небольших чисел, близких к 0, но не к 0.
Шаг-2 → Введите первое наблюдение вашего набора данных во входном слое, каждый объект в одном узле.
Шаг-3 →Прогнозные Размножение: Слева направо, нейроны активируются таким образом, что влияние активации каждого нейрона ограничено весами. Распространять активации до получения предсказанного значения.
Шаг 4 → Сравните прогнозируемый результат с фактическим результатом и измерьте сгенерированную ошибку (функция Cost).
Шаг 5 →Обратное распространение: справа налево ошибка распространяется обратно. Обновите веса в соответствии с тем, насколько они ответственны за ошибку. Скорость обучения решает, сколько мы обновляем весов.
Шаг-6 → Повторите шаги с 1 по 5 и обновляйте веса после каждого наблюдения (Обучение усилению)
Шаг-7 → Когда весь тренировочный комплекс прошел через ANN, это делает и эпоху. Повторяйте больше эпох.
Источник:techcrunch.com
Нейронные сети — это новая концепция, потенциал которой мы только что поцарапали. Они могут использоваться для различных концепций и идей, а также обучаться с помощью специального механизма обратного распространения и исправления ошибок на этапе тестирования. Путем должной минимизации ошибки эти многослойные системы могут однажды изучить и концептуализировать идеи в одиночку, без человеческой коррекции.
Вот и все для этой статьи. В следующей статье мы создадим искусственную нейронную сеть с нуля, используя библиотеку numpy python.
Надеюсь, вам, ребята, понравилось читать это. Пожалуйста, поделитесь своими мыслями / сомнениями в разделе комментариев. Вы можете связаться со мной черезLinkedInдля любого запроса.
Вы можете связаться со мной черезLinkedInдля любого запроса.
Спасибо за чтение!!!
Эта статья была также опубликована наKDnuggets,
Оригинальная статья
Как настроить количество слоев и узлов в нейронной сети
Последнее обновление 6 августа 2019 г.
Искусственные нейронные сети имеют два основных гиперпараметра, которые управляют архитектурой или топологией сети: количество слоев и количество узлов в каждом скрытом слое.
Вы должны указать значения для этих параметров при настройке сети.
Самый надежный способ настроить эти гиперпараметры для конкретной задачи прогнозного моделирования — это систематические эксперименты с надежной тестовой оснасткой.
Это может быть непростая задача для новичков в области машинного обучения, ищущих аналитический способ вычисления оптимального количества слоев и узлов или простых практических правил, которым нужно следовать.
В этом посте вы узнаете о ролях слоев и узлов и о том, как подойти к настройке многослойной нейронной сети персептрона для решения вашей задачи прогнозного моделирования.
Прочитав этот пост, вы будете знать:
- Разница между одноуровневыми и многослойными сетями персептронов.
- Значение наличия одного или нескольких скрытых слоев в сети.
- Пять подходов к настройке количества уровней и узлов в сети.
Начните свой проект с моей новой книги «Лучшее глубокое обучение», включающей пошаговых руководств и файлы исходного кода Python для всех примеров.
Приступим.
Как настроить количество слоев и узлов в нейронной сети
Фотография Райана, некоторые права защищены.
Обзор
Этот пост разделен на четыре раздела; их:
- Многослойный персептрон
- Как подсчитать слои?
- Зачем нужно несколько слоев?
- Сколько слоев и узлов использовать?
Многослойный персептрон
Узел, также называемый нейроном или персептроном, представляет собой вычислительную единицу, которая имеет одно или несколько взвешенных входных соединений, передаточную функцию, которая каким-либо образом объединяет входы, и выходное соединение.
Узлы затем организуются в уровни, составляющие сеть.
Однослойная искусственная нейронная сеть, также называемая однослойной, имеет один слой узлов, как следует из названия. Каждый узел в одном слое напрямую подключается к входной переменной и вносит свой вклад в выходную переменную.
Одноуровневые сети имеют только один уровень активных модулей. Входы подключаются напрямую к выходам через один слой весов. Выходы не взаимодействуют, поэтому сеть с N выходами может рассматриваться как N отдельных сетей с одним выходом.
— страница 15, Neural Smithing: контролируемое обучение в искусственных нейронных сетях с прямой связью, 1999.
Одноуровневая сеть может быть расширена до многоуровневой сети, называемой многоуровневым персептроном. Многослойный персептрон или сокращенно MLP — это искусственная нейронная сеть с более чем одним слоем.
Он имеет входной слой, который соединяется с входными переменными, один или несколько скрытых слоев и выходной слой, который производит выходные переменные.
Стандартный многослойный перцептрон (MLP) представляет собой каскад однослойных перцептронов. Есть слой входных узлов, слой выходных узлов и один или несколько промежуточных уровней. Внутренние слои иногда называют «скрытыми слоями», потому что они не наблюдаются напрямую из входов и выходов системы.
— стр. 31, Neural Smithing: контролируемое обучение в искусственных нейронных сетях с прямой связью, 1999.
Мы можем суммировать типы слоев в MLP следующим образом:
- Входной уровень : Входные переменные, иногда называемые видимым слоем.
- Скрытые слои : Слои узлов между входным и выходным слоями. Этих слоев может быть один или несколько.
- Выходной уровень : Уровень узлов, которые производят выходные переменные.
Наконец, есть термины, используемые для описания формы и возможностей нейронной сети; например:
- Размер : количество узлов в модели.

- Ширина : количество узлов в определенном слое.
- Глубина : количество слоев в нейронной сети.
- Емкость : Тип или структура функций, которые могут быть изучены с помощью конфигурации сети. Иногда называется « представительская емкость ».
- Архитектура : Особое расположение уровней и узлов в сети.
Как посчитать слои?
Традиционно существуют разногласия по поводу того, как считать количество слоев.
Разногласия возникают по поводу того, считается ли входной слой. Есть аргумент в пользу того, что его не следует считать, потому что входы неактивны; они просто входные переменные. Мы будем использовать это соглашение; это также соглашение, рекомендованное в книге « Neural Smithing ».
Следовательно, MLP, имеющий входной слой, один скрытый слой и один выходной слой, является двухуровневым MLP.
Структуру MLP можно описать простыми обозначениями.
Это удобное обозначение суммирует как количество слоев, так и количество узлов в каждом слое. Количество узлов в каждом слое указывается в виде целого числа в порядке от входного уровня до выходного, с размером каждого слоя, разделенным символом прямой косой черты («/»).
Например, сеть с двумя переменными на входном уровне, одним скрытым слоем с восемью узлами и выходным слоем с одним узлом может быть описана с использованием обозначения: 2/8/1.
Я рекомендую использовать это обозначение при описании слоев и их размеров для нейронной сети многослойного персептрона.
Зачем нужны несколько слоев?
Прежде чем мы посмотрим, сколько слоев указать, важно подумать о том, почему нам нужно иметь несколько слоев.
Однослойная нейронная сеть может использоваться только для представления линейно разделимых функций. Это означает очень простые задачи, в которых, скажем, два класса в задаче классификации можно аккуратно разделить линией.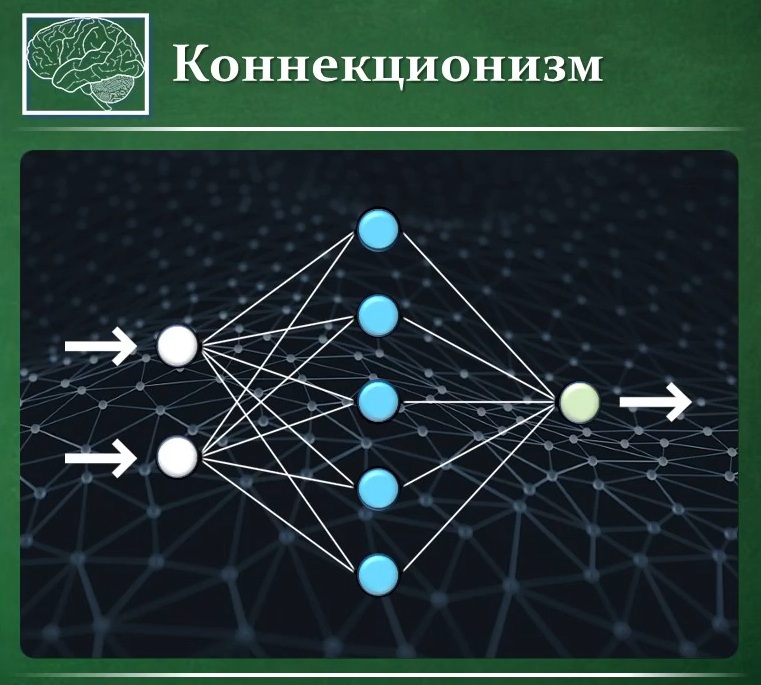 Если ваша проблема относительно проста, возможно, будет достаточно однослойной сети.
Если ваша проблема относительно проста, возможно, будет достаточно однослойной сети.
Большинство задач, которые нас интересуют, не разделимы линейно.
Многослойный персептрон можно использовать для представления выпуклых областей. Это означает, что в действительности они могут научиться рисовать фигуры вокруг примеров в некотором многомерном пространстве, которое может разделять и классифицировать их, преодолевая ограничение линейной разделимости.
Фактически, есть теоретическое открытие Липпмана в статье 1987 года «Введение в вычисления с нейронными сетями», которое показывает, что MLP с двумя скрытыми слоями достаточно для создания областей классификации любой желаемой формы.Это поучительно, хотя следует отметить, что не дается никаких указаний о том, сколько узлов использовать на каждом уровне или как узнать веса.
Дальнейшее теоретическое открытие и доказательство показали, что MLP являются универсальными приближениями. Что с одним скрытым слоем, MLP может аппроксимировать любую функцию, которая нам нужна.
В частности, универсальная аппроксимационная теорема утверждает, что сеть прямого распространения с линейным выходным слоем и по крайней мере одним скрытым слоем с любой функцией активации «раздавливания» (такой как логистическая сигмоидальная функция активации) может аппроксимировать любую измеримую по Борелю функцию от одного конечного — размерное пространство в другое с любой желаемой ненулевой ошибкой, при условии, что в сети достаточно скрытых единиц.
— стр. 198, Глубокое обучение, 2016 г.
Это часто цитируемое теоретическое открытие, и о нем написано множество литературы. На практике мы снова не знаем, сколько узлов использовать в единственном скрытом слое для данной проблемы, а также как эффективно изучить или установить их веса. Кроме того, было представлено множество контрпримеров функций, которые не могут быть изучены напрямую через один MLP с одним скрытым слоем или требуют бесконечного числа узлов.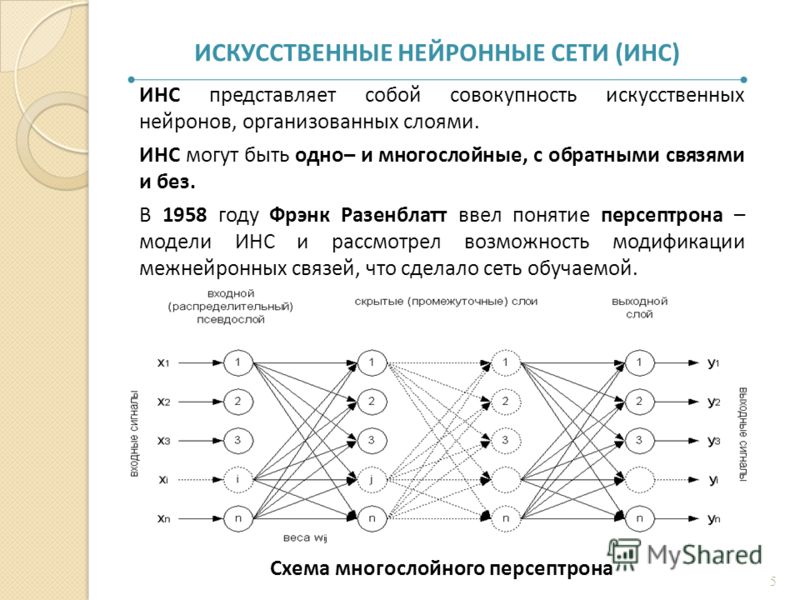
Даже для тех функций, которые могут быть изучены с помощью достаточно большого MLP с одним скрытым слоем, может быть более эффективным изучить его с двумя (или более) скрытыми слоями.
Поскольку один достаточно большой скрытый слой подходит для аппроксимации большинства функций, зачем кому-то использовать больше? Одна причина заключается в словах «достаточно большой». Хотя один скрытый слой оптимален для некоторых функций, существуют другие, для которых решение с одним скрытым слоем очень неэффективно по сравнению с решениями с большим количеством слоев.
— стр. 38, Neural Smithing: контролируемое обучение в искусственных нейронных сетях с прямой связью, 1999.
Сколько слоев и узлов использовать?
С преамбулой MLP, давайте перейдем к вашему настоящему вопросу.
Сколько слоев следует использовать в многослойном персептроне и сколько узлов на каждом слое?
В этом разделе мы перечислим пять подходов к решению этой проблемы.
1) Эксперименты
В общем, когда меня спрашивают, сколько слоев и узлов использовать для MLP, я часто отвечаю:
Не знаю. Используйте систематические эксперименты, чтобы определить, что лучше всего подходит для вашего конкретного набора данных.
Я все еще придерживаюсь этого ответа.
В общем, вы не можете аналитически рассчитать количество слоев или количество узлов, которые будут использоваться на каждом слое в искусственной нейронной сети для решения конкретной реальной проблемы прогнозного моделирования.
Количество слоев и количество узлов в каждом слое — это гиперпараметры модели, которые вы должны указать.
Вы, вероятно, будете первым, кто попытается решить вашу конкретную проблему с помощью нейронной сети. До вас ее никто не решал. Поэтому никто не может подсказать вам ответ, как настроить сеть.
Вы должны найти ответ с помощью надежной испытательной системы и контролируемых экспериментов. Например, см. Сообщение:
Например, см. Сообщение:
Независимо от эвристики, с которой вы можете столкнуться, все ответы будут сводиться к необходимости тщательного экспериментирования, чтобы увидеть, что лучше всего подходит для вашего конкретного набора данных.
2) Интуиция
Сеть можно настроить интуитивно.
Например, у вас может быть интуиция, что для решения конкретной задачи прогнозного моделирования требуется глубокая сеть.
Глубокая модель обеспечивает иерархию уровней, которые создают возрастающие уровни абстракции от пространства входных переменных до выходных переменных.
Учитывая понимание предметной области, мы можем полагать, что для достаточного решения проблемы прогнозирования требуется глубокая иерархическая модель. В этом случае мы можем выбрать конфигурацию сети, которая имеет много уровней глубины.
Выбор глубокой модели закодирует очень общее убеждение, что функция, которую мы хотим изучить, должна включать композицию нескольких более простых функций.С точки зрения репрезентативного обучения это можно интерпретировать как утверждение, что, по нашему мнению, проблема обучения состоит в обнаружении набора основных факторов вариации, которые, в свою очередь, могут быть описаны в терминах других, более простых, лежащих в основе факторов вариации.
— стр. 201, Глубокое обучение, 2016 г.
Эта интуиция может исходить из опыта работы в предметной области, опыта моделирования проблем с нейронными сетями или их сочетания.
По моему опыту, интуиция часто опровергается экспериментами.
3) Глубина
В своем важном учебнике по глубокому обучению Гудфеллоу, Бенжио и Курвиль подчеркивают, что эмпирически по интересующим проблемам глубокие нейронные сети работают лучше.
В частности, они заявляют о выборе использования глубоких нейронных сетей в качестве статистического аргумента в тех случаях, когда глубина может быть интуитивно полезной.
Эмпирически кажется, что большая глубина приводит к лучшему обобщению для широкого круга задач.
[…] Это говорит о том, что использование глубокой архитектуры действительно выражает полезный приоритет над пространством функций, которые модель изучает.
— стр. 201, Глубокое обучение, 2016 г.
Мы можем использовать этот аргумент, чтобы предположить, что использование глубоких сетей с множеством уровней может быть эвристическим подходом к настройке сетей для решения сложных задач прогнозного моделирования.
Это аналогично совету для начала работы со случайным лесом и стохастическим усилением градиента в задаче прогнозного моделирования с табличными данными, чтобы быстро получить представление о верхней границе навыка модели перед тестированием других методов.
4) Заимствовать идеи
Простой, но, возможно, трудоемкий подход, заключается в использовании результатов, опубликованных в литературе.
Найдите исследовательские работы, в которых описывается использование MLP для решения задач прогнозирования, в чем-то похожих на вашу проблему. Обратите внимание на конфигурацию сетей, использованных в этих документах, и используйте их в качестве отправной точки для конфигураций для проверки вашей проблемы.
Переносимость гиперпараметров модели, которая приводит к умелым моделям от одной проблемы к другой, является сложной открытой проблемой и причиной того, почему конфигурация гиперпараметров модели является больше искусством, чем наукой.
Тем не менее, сетевые уровни и количество узлов, используемых для решения связанных проблем, являются хорошей отправной точкой для тестирования идей.
5) Поиск
Разработайте автоматический поиск для тестирования различных сетевых конфигураций.
Вы можете посеять поиск идеями из литературы и интуиции.
Некоторые популярные стратегии поиска включают:
- Случайно : Попробуйте случайные конфигурации слоев и узлов на каждом слое.
- Сетка : попробуйте систематический поиск по количеству слоев и узлов на каждом слое.

- Эвристика : попробуйте направленный поиск по конфигурациям, таким как генетический алгоритм или байесовская оптимизация.
- Исчерпывающий : Попробуйте все комбинации слоев и количества узлов; это может быть осуществимо для небольших сетей и наборов данных.
Это может быть сложно с большими моделями, большими наборами данных и их комбинациями. Некоторые идеи по снижению или управлению вычислительной нагрузкой включают:
- Подгоняйте модели к меньшему подмножеству обучающего набора данных, чтобы ускорить поиск.
- Агрессивно ограничивает размер области поиска.
- Распараллеливайте поиск на нескольких экземплярах сервера (например, используйте сервис Amazon EC2).
Я рекомендую действовать систематически, если позволяют время и ресурсы.
Подробнее
Я видел бесчисленные эвристики, позволяющие оценить количество слоев и либо общее количество нейронов, либо количество нейронов на слой.
Я не хочу их перечислять; Я скептически отношусь к тому, что они добавляют практическую ценность помимо тех особых случаев, на которых они демонстрируются.
Если эта область вам интересна, возможно, начните с « Раздел 4.4. Емкость по сравнению с размером » в книге «Neural Smithing». В нем обобщено множество открытий в этой области. Книга датирована 1999 годом, так что есть еще почти 20 лет идей, которые нужно реализовать в этой области, если вы готовы.
Также см. Некоторые обсуждения, ссылки на которые приведены в разделе Дополнительная литература (ниже).
Скучал по вашему любимому способу настройки нейронной сети? Или знаете хорошую ссылку по теме?
Дайте мне знать в комментариях ниже.
Дополнительная литература
Этот раздел предоставляет дополнительные ресурсы по теме, если вы хотите углубиться.
Документы
Книги
Статьи
Обсуждения
Сводка
В этом посте вы узнали о роли слоев и узлов и о том, как настроить многослойную нейронную сеть персептрона.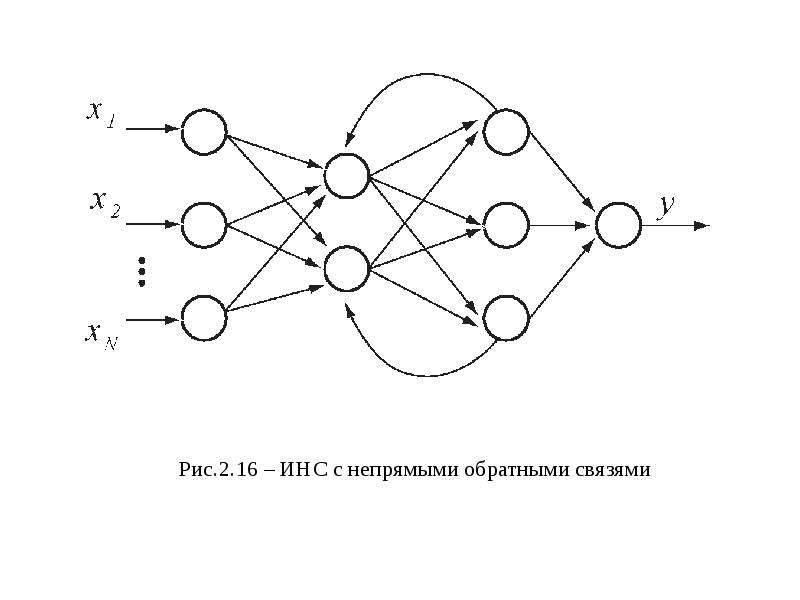
В частности, вы выучили:
- Разница между одноуровневыми и многослойными сетями персептронов.
- Значение наличия одного или нескольких скрытых слоев в сети.
- Пять подходов к настройке количества уровней и узлов в сети.
Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Разрабатывайте лучшие модели глубокого обучения сегодня!
Тренируйтесь быстрее, меньше перетяжек и ансамбли
… всего несколькими строками кода Python
Узнайте, как в моей новой электронной книге:
Better Deep Learning
Он предоставляет руководств для самообучения по таким темам, как:
снижение веса , нормализация партии , выпадение , укладка моделей и многое другое…
Сделайте свои проекты более глубокими!
Пропустить академики. Только результаты.
Посмотрите, что внутри
Однослойные искусственные нейронные сети для анализа экспрессии генов
Аджит Нараянан — профессор искусственного интеллекта в Университете Эксетера, где он работал последние 23 года. Его первая степень была в области коммуникативных наук и лингвистики в Астонском университете (1973), а вторая — докторская степень.Доктор философии в Университете Эксетера (1976). Он начал читать лекции по компьютерным наукам в Университете Эксетера вскоре после создания кафедры (1980 г.). Его интересы связаны с искусственным интеллектом, когнитивными науками и проблемами разума / мозга. Он написал несколько книг и множество статей по ИИ, а недавно стал директором по биоинформатике в Эксетере. Его текущие исследовательские интересы сосредоточены на применении методов искусственного интеллекта к проблемам биоинформатики.
Др.Эдвард Кидвелл защитил докторскую диссертацию. получил степень бакалавра наук с отличием в области компьютерных наук (биоинформатика) в Университете Эксетера в 2003 году. Д-р Кидвелл интересуется применением искусственного интеллекта и методов эволюционных вычислений для оптимизации. проблемы инженерии, а также проблемы биоинформатики. Имеет публикации в ряде журналов и сборников по информатике, биоинформатике и инженерии.В настоящее время он является научным сотрудником Университета Эксетера.
Д-р Кидвелл интересуется применением искусственного интеллекта и методов эволюционных вычислений для оптимизации. проблемы инженерии, а также проблемы биоинформатики. Имеет публикации в ряде журналов и сборников по информатике, биоинформатике и инженерии.В настоящее время он является научным сотрудником Университета Эксетера.
Йонас Гамалиельссон — доктор философии. студент биоинформатики, работающий в Университете Скёвде, Швеция, где он ранее получил степень магистра наук. Кандидат компьютерных наук со специализацией в области искусственного интеллекта и биоинформатики (2001 г.), а также степень бакалавра наук. степень в области компьютерных наук с направлением на разработку программного обеспечения (2000 г.). Его основные исследовательские интересы — алгоритмы интеллектуального анализа данных для анализа многомерных наборов биологических данных, таких как наборы данных экспрессии генов микрочипов, а также разработка алгоритмов для оценки интереса добытых шаблонов и правил с использованием структурированных предшествующих биологических знаний.
Шьям С. Татинени родился и вырос в Южной Индии, изучал медицину в Манипальской академии высшего образования в Карнатаке, Индия. Затем он год проработал интерном в Хайдарабаде, Индия, прежде чем приехать в Эксетерский университет для получения степени магистра наук. в биоинформатике. Его M.Sc. Исследовательский проект включал использование нейронных сетей для анализа данных экспрессии генов. После получения степени магистра наук он присоединился к компании Novartis Pharmaceuticals в Базеле, Швейцария, где в настоящее время работает с командой из четырех специалистов по биоинформатике над проектом сравнительной геномики.Он также разрабатывает новый браузер генома, который можно использовать для просмотра различных участков генома вместе с данными, полученными от компании.
Copyright © 2003 Elsevier B.V. Все права защищены.
Краткое введение в нейронные сети — блог по науке о данных
Искусственная нейронная сеть (ИНС) — это вычислительная модель, вдохновленная тем, как биологические нейронные сети обрабатывают информацию в человеческом мозгу. Искусственные нейронные сети вызвали большой интерес в исследованиях и промышленности машинного обучения благодаря множеству прорывных результатов в распознавании речи, компьютерном зрении и обработке текста.В этом сообщении в блоге мы попытаемся понять особый тип искусственной нейронной сети, называемый многоуровневым персептроном.
Искусственные нейронные сети вызвали большой интерес в исследованиях и промышленности машинного обучения благодаря множеству прорывных результатов в распознавании речи, компьютерном зрении и обработке текста.В этом сообщении в блоге мы попытаемся понять особый тип искусственной нейронной сети, называемый многоуровневым персептроном.
Одиночный нейрон
Базовой единицей вычислений в нейронной сети является нейрон , часто называемый узлом или блоком . Он получает ввод от некоторых других узлов или от внешнего источника и вычисляет вывод. Каждому входу соответствует вес (w), который присваивается на основе его относительной важности по отношению к другим входам.Узел применяет функцию f (определенную ниже) к взвешенной сумме своих входов, как показано на рисунке 1 ниже:
Рисунок 1: одиночный нейрон
Вышеупомянутая сеть принимает числовые входы X1 и X2 и имеет веса w1 и w2 , связанные с этими входами. Кроме того, есть еще один вход 1 с весом b (называемый Bias ), связанный с ним.Подробнее о роли предвзятости мы узнаем позже.
Выходной сигнал Y нейрона вычисляется, как показано на рисунке 1. Функция f является нелинейной и называется функцией активации . Назначение функции активации — внести нелинейность в выходной сигнал нейрона. Это важно, потому что большинство реальных данных нелинейны, и мы хотим, чтобы нейроны изучали эти нелинейные представления .
Каждая функция активации ( или нелинейность ) принимает одно число и выполняет над ним определенную фиксированную математическую операцию [2]. Есть несколько функций активации, с которыми вы можете столкнуться на практике:
- Сигмоид: принимает ввод с действительным знаком и сжимает его до диапазона от 0 до 1
σ (x) = 1 / (1 + ехр (−x))
- tanh: принимает ввод с действительным знаком и сжимает его до диапазона [-1, 1]
tanh (x) = 2σ (2x) — 1
- ReLU : ReLU расшифровывается как Rectified Linear Unit.
 Он принимает входные данные с действительным знаком и устанавливает его пороговое значение на ноль (заменяет отрицательные значения на ноль)
Он принимает входные данные с действительным знаком и устанавливает его пороговое значение на ноль (заменяет отрицательные значения на ноль)
f (x) = макс (0, x)
На рисунках ниже [2] показаны все вышеперечисленные функции активации.
Рисунок 2: различные функции активации
Важность смещения: Основная функция смещения — предоставить каждому узлу обучаемое постоянное значение (в дополнение к обычным входным данным, которые этот узел получает). См. Эту ссылку, чтобы узнать больше о роли смещения в нейроне.
Нейронная сеть прямого распространения
Нейронная сеть с прямой связью была первым и самым простым типом созданной искусственной нейронной сети [3]. Он содержит несколько нейронов (узлов), расположенных в слоях . Узлы из соседних слоев имеют соединений, или ребер, между собой. Все эти соединения имеют весов , связанных с ними.
Пример нейронной сети с прямой связью показан на рисунке 3.
Рисунок 3: пример нейронной сети с прямой связью
Нейронная сеть прямого распространения может состоять из узлов трех типов:
- Узлы ввода — Узлы ввода предоставляют информацию из внешнего мира в сеть и вместе называются «Уровень ввода».Никакие вычисления не выполняются ни на одном из узлов ввода — они просто передают информацию скрытым узлам.
- Скрытые узлы — Скрытые узлы не имеют прямой связи с внешним миром (отсюда и название «скрытые»). Они выполняют вычисления и передают информацию от входных узлов к выходным узлам. Набор скрытых узлов образует «Скрытый слой». В то время как сеть с прямой связью будет иметь только один входной слой и один выходной слой, она может иметь ноль или несколько скрытых слоев.
- Узлы вывода — Узлы вывода вместе называются «Уровень вывода» и отвечают за вычисления и передачу информации из сети во внешний мир.

В сети прямого распространения информация перемещается только в одном направлении — вперед — от входных узлов через скрытые узлы (если есть) и к выходным узлам. В сети нет циклов или петель [3] (это свойство сетей с прямой связью отличается от рекуррентных нейронных сетей, в которых соединения между узлами образуют цикл).
Два примера сетей прямого распространения приведены ниже:
Однослойный персептрон — это простейшая нейронная сеть прямого распространения [4], не содержащая скрытых слоев. Вы можете узнать больше об однослойных персептронах в [4], [5], [6], [7].
Многослойный персептрон — Многослойный персептрон имеет один или несколько скрытых слоев. Ниже мы обсудим только многослойные персептроны, поскольку они более полезны, чем однослойные персептоны для практических приложений сегодня.
Многослойный персептрон
Многослойный персептрон (MLP) содержит один или несколько скрытых слоев (кроме одного входного и одного выходного). В то время как однослойный персептрон может изучать только линейные функции, многослойный персептрон также может изучать нелинейные функции.
На рисунке 4 показан многослойный персептрон с единственным скрытым слоем. Обратите внимание, что все соединения имеют веса, связанные с ними, но только три веса (w0, w1, w2) показаны на рисунке.
Входной уровень: Входной слой состоит из трех узлов. Узел Bias имеет значение 1. Два других узла принимают X1 и X2 в качестве внешних входов (которые представляют собой числовые значения, зависящие от входного набора данных). Как обсуждалось выше, на входном уровне вычисления не выполняются, поэтому выходными данными от узлов на входном уровне являются 1, X1 и X2 соответственно, которые передаются на скрытый уровень.
Скрытый слой: Скрытый слой также имеет три узла, а узел смещения имеет выходное значение 1.Выходные данные двух других узлов в скрытом слое зависят от выходных данных входного слоя (1, X1, X2), а также весов, связанных с соединениями (ребрами). На рисунке 4 показан расчет выходных данных для одного из скрытых узлов (выделен). Аналогичным образом может быть рассчитан вывод от другого скрытого узла. Помните, что f относится к функции активации. Эти выходные данные затем передаются в узлы выходного слоя.
На рисунке 4 показан расчет выходных данных для одного из скрытых узлов (выделен). Аналогичным образом может быть рассчитан вывод от другого скрытого узла. Помните, что f относится к функции активации. Эти выходные данные затем передаются в узлы выходного слоя.
Рисунок 4: многослойный персептрон, имеющий один скрытый слой
Выходной уровень: Выходной слой имеет два узла, которые принимают входные данные из скрытого слоя и выполняют аналогичные вычисления, как показано для выделенного скрытого узла.Значения, вычисленные (Y1 и Y2) в результате этих вычислений, действуют как выходные данные многослойного персептрона.
Учитывая набор функций X = (x1, x2,…) и цель y , многоуровневый персептрон может изучить взаимосвязь между функциями и целью для классификации или регрессии.
Давайте рассмотрим пример, чтобы лучше понять многослойные персептроны. Предположим, у нас есть следующий набор данных об оценках учащихся:
Два столбца ввода показывают количество часов, которые студент изучил, и средние оценки, полученные студентом.В столбце «Итоговый результат» могут быть два значения: 1 или 0, указывающие, сдал ли студент последний семестр. Например, мы можем видеть, что если студент учился 35 часов и получил 67 баллов в середине семестра, он / она в конечном итоге сдал последний семестр.
Теперь предположим, что мы хотим предсказать, пройдет ли последний семестр студент, изучающий 25 часов и получивший 70 оценок в середине семестра.
Это проблема двоичной классификации, когда многослойный перцептрон может учиться на приведенных примерах (обучающих данных) и делать обоснованное предсказание с учетом новой точки данных.Ниже мы увидим, как многослойный перцептрон изучает такие отношения.
Обучение нашего MLP: алгоритм обратного распространения
Процесс обучения многослойного персептрона называется алгоритмом обратного распространения. Я бы рекомендовал прочитать этот ответ Quora Хеманта Кумара (цитируется ниже), который ясно объясняет обратное распространение.
Я бы рекомендовал прочитать этот ответ Quora Хеманта Кумара (цитируется ниже), который ясно объясняет обратное распространение.
Обратное распространение ошибок, , часто сокращенно BackProp, является одним из нескольких способов обучения искусственной нейронной сети (ИНС).Это контролируемая схема обучения, что означает, что она учится на помеченных данных обучения (есть супервизор, который руководит ее обучением).
Проще говоря, BackProp похож на « учимся на ошибках ». Супервизор исправляет ИНС всякий раз, когда он делает ошибки.
ИНС состоит из узлов на разных уровнях; входной слой, промежуточный скрытый слой (и) и выходной слой. Связи между узлами соседних слоев имеют связанные с ними «веса».Цель обучения — присвоить этим ребрам правильные веса. Учитывая входной вектор, эти веса определяют выходной вектор.
При обучении с учителем обучающая выборка помечена. Это означает, что для некоторых данных входов мы знаем желаемый / ожидаемый результат (метку).
BackProp Algorithm:
Первоначально все веса ребер назначаются случайным образом. Для каждого ввода в наборе обучающих данных активируется ИНС и отслеживается ее вывод. Этот результат сравнивается с желаемым результатом, который мы уже знаем, и ошибка «распространяется» обратно на предыдущий уровень.Эта ошибка отмечается, и веса корректируются соответствующим образом. Этот процесс повторяется до тех пор, пока ошибка вывода не станет ниже заранее определенного порога.Как только вышеуказанный алгоритм завершается, у нас есть «обученная» ИНС, которая, как мы считаем, готова работать с «новыми» входными данными. Сообщается, что эта ИНС извлекла уроки из нескольких примеров (помеченные данные) и из своих ошибок (распространение ошибок).
Теперь, когда у нас есть представление о том, как работает обратное распространение, давайте вернемся к нашему набору данных студенческих оценок, показанному выше.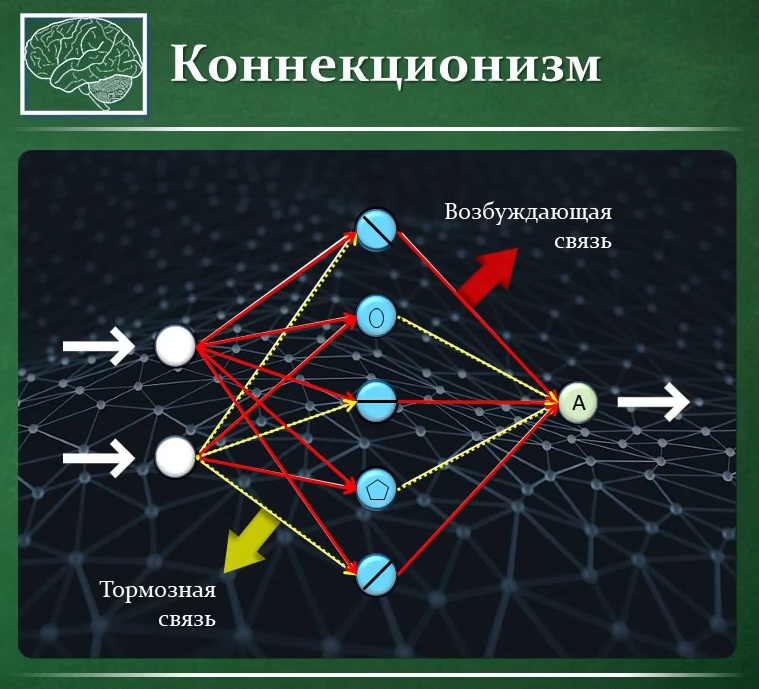
Многослойный персептрон, показанный на рисунке 5 (адаптированный из превосходного визуального объяснения алгоритма обратного распространения ошибки Себастьяна Рашки), имеет два узла на входном уровне (кроме узла смещения), которые принимают входные данные «Часы работы» и «Промежуточные оценки». . Он также имеет скрытый слой с двумя узлами (кроме узла Bias). Выходной уровень также имеет два узла — верхний узел выводит вероятность «Пройдено», а нижний узел выводит вероятность «Неудача».
В задачах классификации мы обычно используем функцию Softmax в качестве функции активации на выходном уровне многослойного персептрона, чтобы гарантировать, что выходы являются вероятностями и в сумме дают 1.Функция Softmax берет вектор произвольных действительных оценок и сжимает его до вектора значений от нуля до единицы, сумма которых равна единице. Итак, в данном случае
Вероятность (пройден) + Вероятность (неудача) = 1
Шаг 1. Прямое распространение
Все веса в сети назначаются случайным образом. Давайте рассмотрим узел скрытого уровня, обозначенный V на рисунке 5 ниже. Предположим, что веса соединений от входов к этому узлу равны w1, w2 и w3 (как показано).
Затем сеть принимает первый обучающий пример в качестве входных данных (мы знаем, что для входных данных 35 и 67 вероятность успешного выполнения равна 1).
- Вход в сеть = [35, 67]
- Желаемый выход из сети (цель) = [1, 0]
Тогда выход V из рассматриваемого узла можно рассчитать, как показано ниже ( f — функция активации, такая как сигмовидная):
V = f (1 * w1 + 35 * w2 + 67 * w3)
Аналогичным образом рассчитываются выходы из другого узла в скрытом слое.Выходы двух узлов в скрытом слое действуют как входы для двух узлов в выходном слое. Это позволяет нам вычислить вероятности выхода из двух узлов в выходном слое.
Предположим, что вероятности выхода из двух узлов в выходном слое равны 0,4 и 0,6 соответственно (поскольку веса назначаются случайным образом, выходы также будут случайными).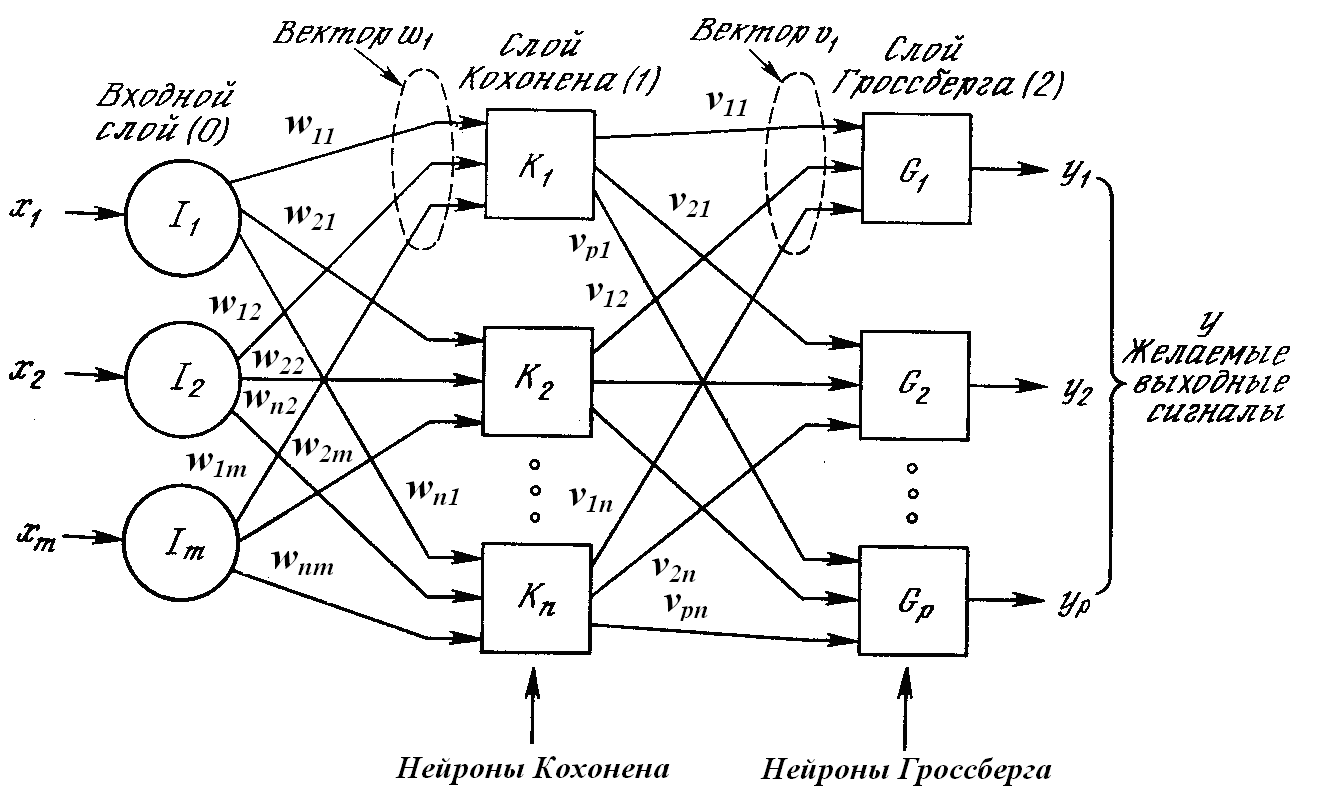 Мы видим, что рассчитанные вероятности (0,4 и 0,6) очень далеки от желаемых вероятностей (1 и 0 соответственно), поэтому говорят, что сеть на рисунке 5 имеет «неправильный результат».
Мы видим, что рассчитанные вероятности (0,4 и 0,6) очень далеки от желаемых вероятностей (1 и 0 соответственно), поэтому говорят, что сеть на рисунке 5 имеет «неправильный результат».
Рисунок 5: шаг прямого распространения в многослойном персептроне
Шаг 2: Обратное распространение и обновление веса
Мы вычисляем общую ошибку на выходных узлах и распространяем эти ошибки обратно по сети, используя обратное распространение для вычисления градиентов . Затем мы используем метод оптимизации, такой как Gradient Descent , чтобы «скорректировать» все веса в сети с целью уменьшения ошибки на выходном слое.Это показано на рисунке 6 ниже (пока игнорируйте математические уравнения на рисунке).
Предположим, что новые веса, связанные с рассматриваемым узлом, — это w4, w5 и w6 (после обратного распространения и корректировки весов).
Рисунок 6. Шаг обратного распространения и обновления веса в многослойном персептроне
Если мы теперь снова введем тот же пример в сеть, сеть должна работать лучше, чем раньше, поскольку теперь веса были скорректированы, чтобы минимизировать ошибку предсказания.Как показано на рисунке 7, ошибки на выходных узлах теперь уменьшаются до [0,2, -0,2] по сравнению с [0,6, -0,4] ранее. Это означает, что наша сеть научилась правильно классифицировать наш первый обучающий пример.
Рисунок 7: сеть MLP теперь лучше работает на том же входе
Мы повторяем этот процесс со всеми другими обучающими примерами в нашем наборе данных. Затем говорят, что наша сеть изучила таких примеров.
Если мы теперь хотим предсказать, пройдет ли последний семестр студент, изучающий 25 часов и получивший 70 баллов в середине семестра, мы проходим этап прямого распространения и находим выходные вероятности для успешных и неуспешных результатов.
Здесь я избегал математических уравнений и объяснения таких понятий, как «градиентный спуск», а скорее попытался развить интуицию для алгоритма. Для более математически сложного обсуждения алгоритма обратного распространения ошибки перейдите по этой ссылке.
Для более математически сложного обсуждения алгоритма обратного распространения ошибки перейдите по этой ссылке.
Трехмерная визуализация многослойного персептрона
Адам Харли создал трехмерную визуализацию многослойного персептрона, который уже был обучен (с использованием обратного распространения ошибки) в базе данных рукописных цифр MNIST.
Сеть принимает 784 числовых значения пикселей в качестве входных данных из изображения 28 x 28 рукописной цифры (у нее 784 узла на входном слое, соответствующих пикселям). Сеть имеет 300 узлов на первом скрытом уровне, 100 узлов на втором скрытом уровне и 10 узлов на выходном уровне (что соответствует 10 цифрам) [15].
Хотя описанная здесь сеть намного больше (использует больше скрытых слоев и узлов) по сравнению с той, которую мы обсуждали в предыдущем разделе, все вычисления на этапе прямого и обратного распространения выполняются таким же образом (на каждом узле), что и обсуждалось ранее.
На рисунке 8 показана сеть, когда на входе цифра «5».
Рисунок 8: визуализация сети для входа «5»
Узел с более высоким выходным значением, чем другие, представлен более ярким цветом. На входном слое яркие узлы — это те узлы, которые получают на входе более высокие числовые значения пикселей. Обратите внимание, как в выходном слое единственный яркий узел соответствует цифре 5 (у него вероятность выхода 1, что выше, чем у других девяти узлов, у которых вероятность выхода равна 0).Это указывает на то, что MLP правильно классифицировал входную цифру. Я настоятельно рекомендую поиграть с этой визуализацией и наблюдать за связями между узлами разных слоев.
Глубокие нейронные сети
- В чем разница между глубоким обучением и обычным машинным обучением?
- В чем разница между нейронной сетью и глубокой нейронной сетью?
- Чем глубокое обучение отличается от многослойного персептрона?
Заключение
Я пропустил важные детали некоторых концепций, обсуждаемых в этом посте, чтобы облегчить понимание.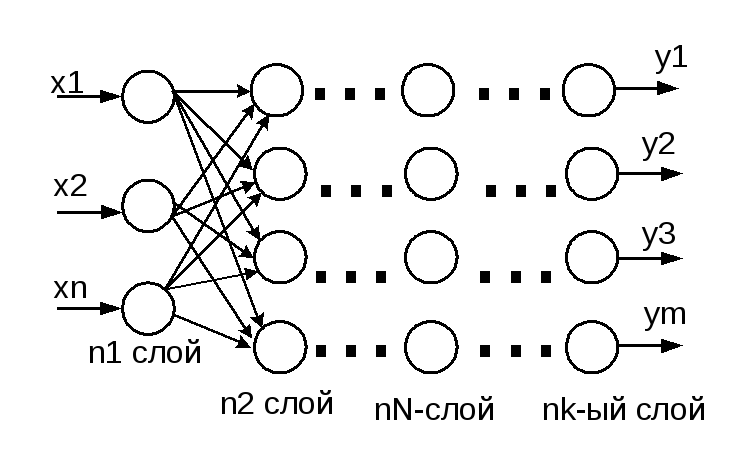 Я бы порекомендовал пройти часть 1, часть 2, часть 3 и практический пример из учебника Стэнфордской нейронной сети для полного понимания многослойных персептронов.
Я бы порекомендовал пройти часть 1, часть 2, часть 3 и практический пример из учебника Стэнфордской нейронной сети для полного понимания многослойных персептронов.
Дайте мне знать в комментариях ниже, если у вас есть какие-либо вопросы или предложения!
Список литературы
- Модели искусственных нейронов
- Нейронные сети, часть 1: Настройка архитектуры (Учебное пособие по Stanford CNN)
- Статья в Википедии о нейронной сети прямого распространения
- Статья в Википедии о Персептроне
- Однослойные нейронные сети (персептроны)
- Однослойный персептрон
- Взвешенные сети — Персептрон
- Модели нейронных сетей (контролируемые) (scikit learn documentation)
- Что вычисляет скрытый слой в нейронной сети?
- Как выбрать количество скрытых слоев и узлов в нейронной сети прямого распространения?
- Сбой Введение в искусственные нейронные сети
- Зачем нужен смещение в ИНС? Должны ли мы иметь отдельный BIAS для каждого слоя?
- Базовое руководство по нейронной сети — Теория
- : демистификация (серия видео): часть 1, Welch Labs @ MLconf SF
- А.У. Харли, «Интерактивная визуализация узловых соединений сверточных нейронных сетей», в ISVC, страницы 867-877, 2015 (ссылка)
Нейронные сети
Однослойные нейронные сети в машинном обучении (персептроны)
Эта статья изначально была опубликована на Codeperfectplus.
Введение
Изучению человеческого мозга уже тысячи лет. Первый шаг к искусственным нейронным сетям был сделан в 1943 году, когда нейрофизиолог Уоррен МакКаллох и молодой математик Уолтер Питтс написали статью о том, как нейроны могут работать.Они смоделировали простую нейронную сеть с электрическими цепями.
Персептроны
Perceptron — это алгоритм двоичной линейной классификации. Это контролируемый тип машинного обучения и простейшая форма нейронной сети. Это база нейронных сетей. Итак, если вы хотите узнать, как работает нейронная сеть, узнайте, как работает восприятие.
Это база нейронных сетей. Итак, если вы хотите узнать, как работает нейронная сеть, узнайте, как работает восприятие.
Компонент перцептронов
Это основные компоненты перцептронов.
- Входное значение
- Вес и смещение
- Чистая сумма
- Функция активации
Входное значение : — Входные значения — это особенность набора данных.
Вес и смещение : — Веса — это значения, которые вычисляются во время обучения модели. Сначала мы начинаем значение весов с некоторого начального значения, и эти значения обновляются для каждой обучающей основы функции ошибок.
Смещение похоже на точку пересечения, добавленную в линейное уравнение. Это дополнительный параметр в нейронной сети, который используется для настройки вывода вместе с взвешенной суммой входов нейрона.Это помогает обучать модель быстрее и качественнее.
Чистая сумма : — Чистая сумма — это сумма произведения входных данных и веса.
NetSum = Σwi.xi
Чистая сумма = Σ w_i. x_i
NetSum = Σwi .xi
Функция активации : — Функция активации используется, чтобы сделать нейронную сеть нелинейной. Он ограничивает вывод от 0 до 1.
Любые комментарии или если у вас есть вопросы, напишите их в комментариях.
Рад быть полезным.
Еще статьи по авторам
Присоединяйтесь к еженедельным обновлениям.
Однослойные нейронные сети в R-программировании
Нейронные сети, также известные как нейронные сети, представляют собой тип алгоритма в машинном обучении и искусственном интеллекте, который работает так же, как человеческий мозг. Искусственные нейроны в нейронной сети демонстрируют то же поведение нейронов в человеческом мозгу. Нейронные сети используются для анализа рисков бизнеса, прогнозирования продаж и многого другого. Нейронные сети адаптируются к изменению входных данных, поэтому нет необходимости снова разрабатывать алгоритм на основе входных данных. В этой статье мы обсудим однослойную нейронную сеть с ее синтаксисом и реализацию функции нейронной сети
Нейронные сети адаптируются к изменению входных данных, поэтому нет необходимости снова разрабатывать алгоритм на основе входных данных. В этой статье мы обсудим однослойную нейронную сеть с ее синтаксисом и реализацию функции нейронной сети () в R-программировании. Для следующей функции требуется нейронная сеть .
Типы нейронных сетей
Нейронные сети можно разделить на несколько типов в зависимости от их фильтров активации глубины, структуры, используемых нейронов, плотности нейронов, потока данных и т. Д.Типы нейронных сетей следующие:
- Персептрон
- Нейронные сети прямого распространения
- Сверточные нейронные сети
- Нейронные сети с радиальной базисной функцией
- Рекуррентные нейронные сети
- Модель последовательности в последовательность
- Модульная нейронная сеть
В зависимости от количества слоев существует два типа нейронных сетей:
- Однослойная нейронная сеть: Однослойная нейронная сеть содержит входной и выходной уровни.Входной слой принимает входные сигналы, а выходной слой соответственно генерирует выходные сигналы.
- Многослойная нейронная сеть: Многослойная нейронная сеть содержит ввод, вывод и один или несколько скрытых слоев. Скрытые слои выполняют промежуточные вычисления перед направлением ввода на выходной слой.
Однослойная нейронная сеть
Однослойная нейронная сеть, часто называемая персептронами, представляет собой тип нейронной сети с прямой связью, состоящей из входных и выходных слоев.Предоставленные входные данные многомерны. Персептроны по своей природе ациклические. Сумма произведения весов и входных данных вычисляется в каждом узле. Входной слой передает сигналы выходному слою. Выходной слой выполняет вычисления. Персептрон может изучать только линейную функцию и требует меньшего количества обучающих данных. Выход может быть представлен одним или двумя значениями (0 или 1).
Выход может быть представлен одним или двумя значениями (0 или 1).
Реализация в R
Язык
R предоставляет функцию neuralnet () , которая доступна в пакете neuralnet для создания одноуровневой нейронной сети.
Синтаксис:
нейронная сеть (формула, данные, скрыто)Параметры:
формула: представляет формулу, на которую должна быть установлена модель
данные: представляют фрейм данных
скрыто: представляет количество нейронов в скрытых слояхЧтобы узнать о дополнительных параметрах функции, используйте следующую команду в консоли: help («нейронная сеть»)
Пример 1:
В этом примере давайте создадим одиночный- слоистая нейронная сеть или перцептрон видов растений ириса setosa и versicolor в зависимости от длины и ширины чашелистиков.
Шаг 1: Установите необходимый пакет
|
Шаг 2: Загрузите пакет
3: Загрузить набор данных
Шаг 4: Подбор нейронной сети
|
Шаг 5: Построение нейронной сети
Вывод: Пример 2:
Шаг 2: Загрузите пакет 3: Загрузить набор данных Шаг 4: Настройка нейронной сети
Шаг 5: Постройте нейронную сеть
Шаг 6: Создать тестовый набор данных
|
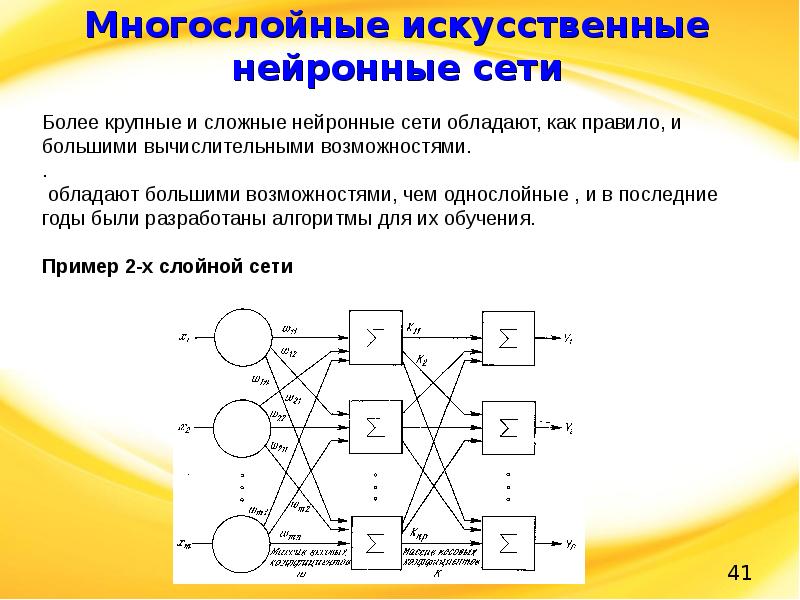 Задача обучения многослойного персептрона. Последовательный и пакетный режимы обучения. Общая схема обучения.
Задача обучения многослойного персептрона. Последовательный и пакетный режимы обучения. Общая схема обучения.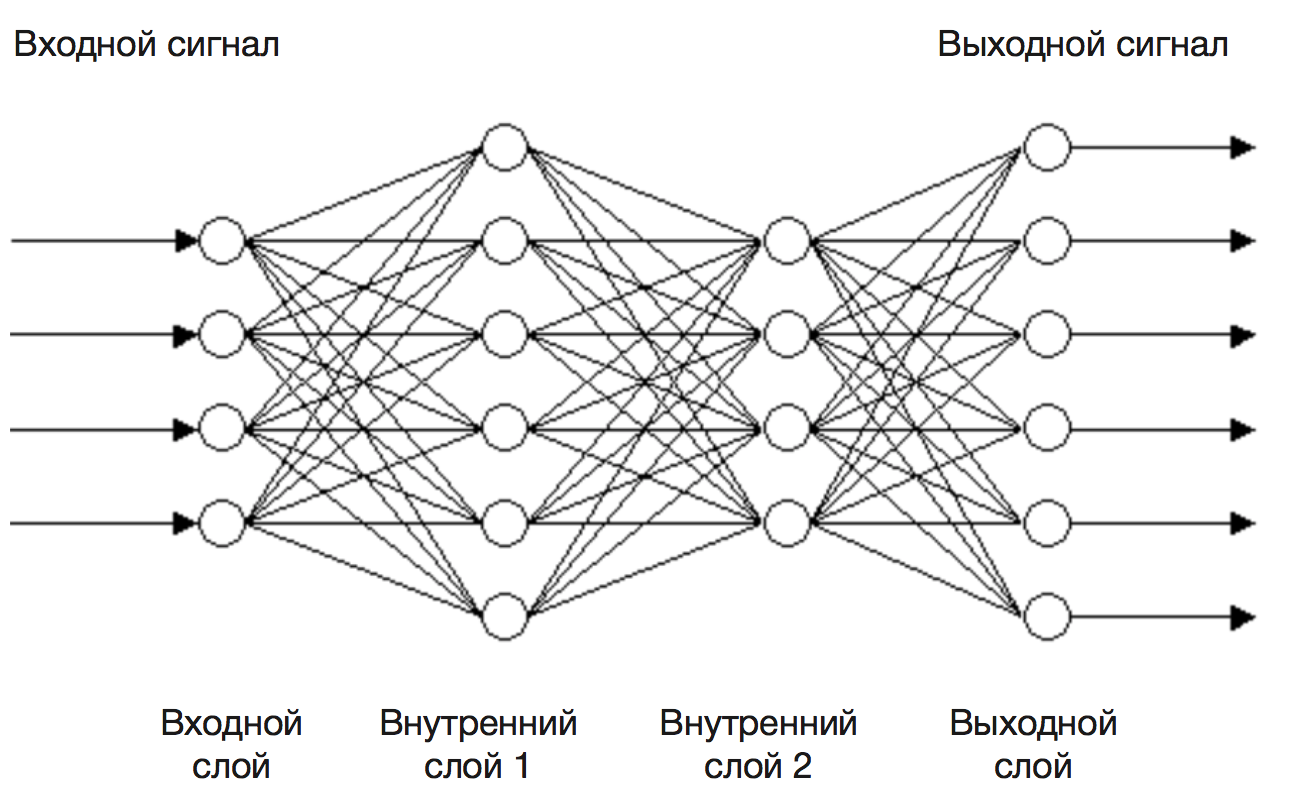
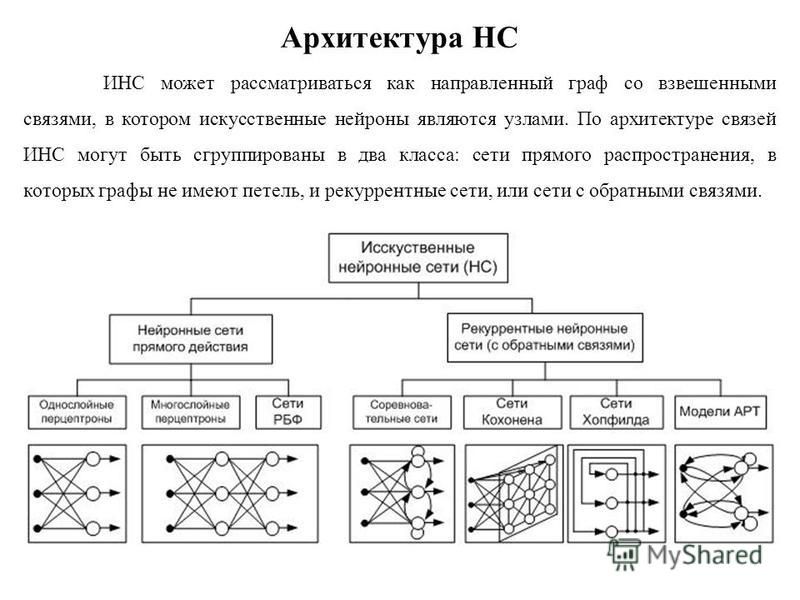 Структура и функционирование сети ВАМ. Кодирование и восстановление запомненных ассоциаций. Обучение по правилу Коско. Модифицированный алгоритм обучения сети ВАМ. Модифицированная структура сети ВАМ и её функционирование. Емкость сетей ВАМ. Примеры применения сетей ВАМ.
Структура и функционирование сети ВАМ. Кодирование и восстановление запомненных ассоциаций. Обучение по правилу Коско. Модифицированный алгоритм обучения сети ВАМ. Модифицированная структура сети ВАМ и её функционирование. Емкость сетей ВАМ. Примеры применения сетей ВАМ.
 Поскольку каждый выходной элемент является независимым от других (каждый вес влияет только на один из выходов), можно ограничиться в нашем исследовании рассмотрением персептронов с единственным выходным элементом, как показано на рис. 20.19, а.
Поскольку каждый выходной элемент является независимым от других (каждый вес влияет только на один из выходов), можно ограничиться в нашем исследовании рассмотрением персептронов с единственным выходным элементом, как показано на рис. 20.19, а. Правильные (эталонные) выходные сигналы при этом не демонстрируются.
Правильные (эталонные) выходные сигналы при этом не демонстрируются. […] Это говорит о том, что использование глубокой архитектуры действительно выражает полезный приоритет над пространством функций, которые модель изучает.
[…] Это говорит о том, что использование глубокой архитектуры действительно выражает полезный приоритет над пространством функций, которые модель изучает.
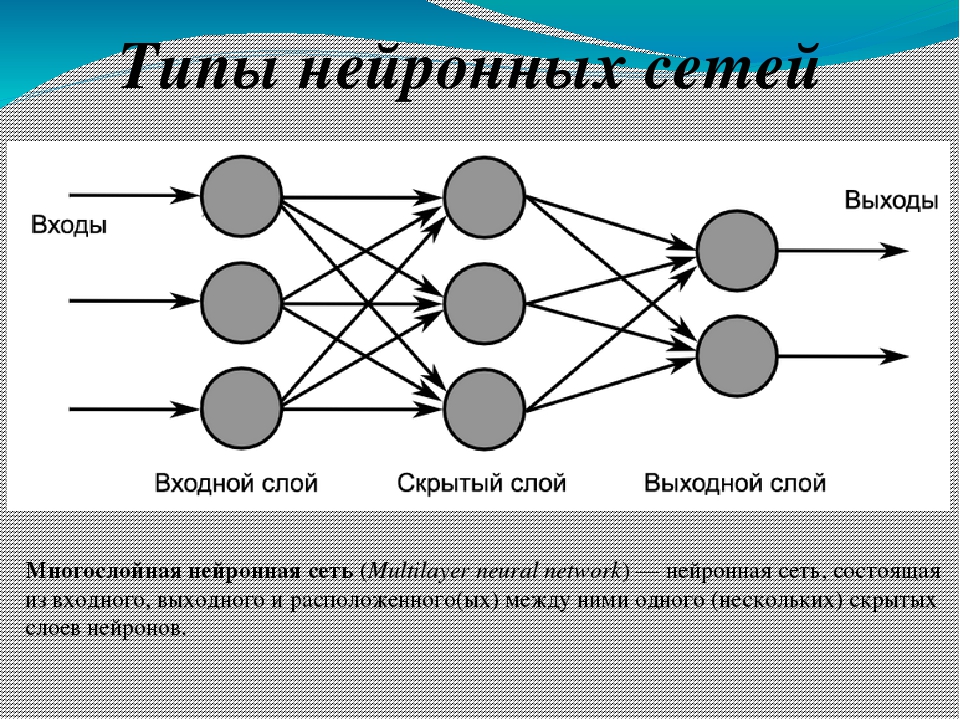 Он принимает входные данные с действительным знаком и устанавливает его пороговое значение на ноль (заменяет отрицательные значения на ноль)
Он принимает входные данные с действительным знаком и устанавливает его пороговое значение на ноль (заменяет отрицательные значения на ноль)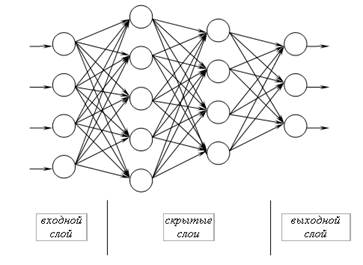 png"
png" 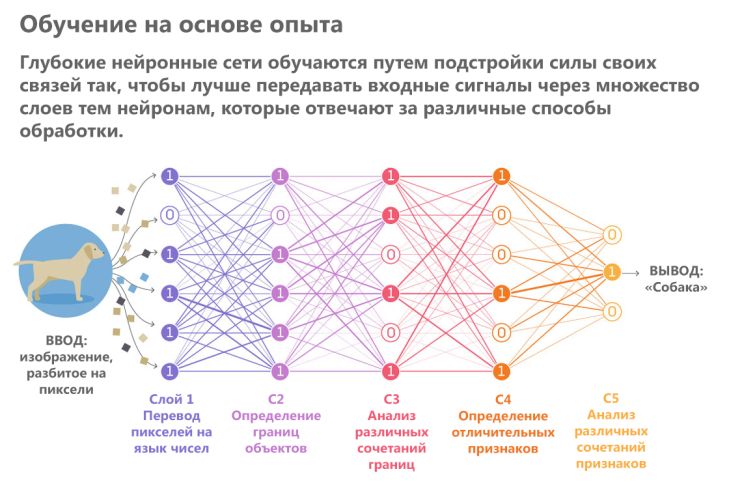 с. =
с. = 
 Однако, если результат не соответствует желаемому, тогда необходимо изменить веса, чтобы уменьшить ошибку.
Однако, если результат не соответствует желаемому, тогда необходимо изменить веса, чтобы уменьшить ошибку.