Криптография и математика: Занимательная криптография
Криптография. Наука о шифрах
Криптография. Наука о шифрах
Габуева А.А. 1
1МБОУ СОШ №30
Караева Д.А. 1
1МБОУ СОШ №30
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Совсем недавно посмотрев как мой друг пишет пароль на телефоне, я задумалась: «Очень ли важны шифры, к какой науке они принадлежат, легко ли расшифровать шифр?» Именно поэтому в этой исследовательской работе рассмотрены методы шифрования, их использование в практической жизни, описанна история создания науки изучающей шифры-криптографии.
Моя цель — изучить методы шифрования, научиться ими пользоваться в практической жизни и узнать, как создавалась КРИПТОГРАФИЯ. А моя гипотеза — «Шифр это то, без чего жизнь со времен, когда люди только научились писать и по настоящее время, невозможно представить».
А моя гипотеза — «Шифр это то, без чего жизнь со времен, когда люди только научились писать и по настоящее время, невозможно представить».
Основная часть.
Математика очень интересная наука для меня , как в школе на уроках, так и в обычной жизни. «Математика гимнастика ума!», — говорил величайший немецкий математик всех времен Карл Фридрих Гаусс. На самом деле мы и не замечаем насколько важная эта наука, но я знаю точно – она используется мною ежедневно. Один из простейших примеров этому – расчеты при покупке продуктов в магазине.
Наука Криптография, называемая также криптологией, является именно тем разделом математики, которая изучает тайнопись (криптография), а так же способы её расшифровки (криптоанализ).
Цель криптографической системы заключается в том, чтобы зашифровать имеющийся начальный текст (исходный текст), получив в итоге полностью непонятный на взгляд шифрованный текст (шифртекст, криптограмма). Адресат, которому он предназначен, должен уметь расшифровать (говорят также «дешифровать») этот шифртекст, восстановив, таким образом, соответствующий ему начальный текст. Криптография предполагает наличие трех компонентов: данных, ключа и криптографического преобразования.
Адресат, которому он предназначен, должен уметь расшифровать (говорят также «дешифровать») этот шифртекст, восстановив, таким образом, соответствующий ему начальный текст. Криптография предполагает наличие трех компонентов: данных, ключа и криптографического преобразования.
Итак, шифрование — это преобразовательный ход: исходный текст, который носит также название открытого текста, заменяется уже зашифрованным текстом.
Дешифрование — обратная шифрованию процедура. На основе ключа шифрованный текст превращается в исходный.
Ключ — информация, необходимая для беспрепятственного шифрования и дешифрования текстов.
Криптография на нашей Земле уже более 4 тысяч лет. Довольно большой срок. Это доказывают исторические документы нескольких древних стран, в особенности Индии, Китая, Египта и Мессопотамии. Однако исследования в этом разделе математики появились совсем недавно.
Однако исследования в этом разделе математики появились совсем недавно.
Если у алфавита буквы, тогда у криптографии-шифры!!! Шифры это именно те цифырки, которые используются во многих случаях современной человеческой жизни. Но криптография это не только тайнопись но и ещё защита данных, защита нашей конфидициальности. Один из примеров защиты наших данных шифрованием – это пароль на телефоне. Ведь не многие любят, когда кто- то из посторонних копается в вашем телефоне. Между тем сегодня шифрование на разных уровнях применяется буквально везде — от простого пароля на телефоне до многоуровневых систем защиты файлов ранга top secret. Мы встречаемся с ней, вставляя карточку в прорезь банкомата, совершая денежные переводы и покупки через интернет, болтая по Skype, отправляя письмо по e-mail и т. д.
Где же возникли первые шифры? Сейчас и узнаем!
Почти 4 тысячи лет назад на берегу Нила египетский писец написал иероглифы. Вельможа Хнумхотел который жил около 19 века до нашей эры написал текст в гробнице, правда не все иероглифы в этом тексте были привычными. Многие из них были заменены на шифр «Скиталла». «Скиталла»-это шифр Древней Спарты. Между прочим он является одним из более старинных устройств криптографии. Это устройство так же использовалось в войне между Спартой и Афинами. Но как же оно выглядело и в чем состаяла его судь? Оно представляло собой длинный стержень (карандаш, палку) на который наматывали пергаментовую ленту(собственно шифр). Но самое интересное, что текст наносился на ленту в начале с одной стороны сверху вниз, а затем уже с другой, Таким образом, когда разматывали ленту не возможно было понять, что зашифрованно на ней!
Вельможа Хнумхотел который жил около 19 века до нашей эры написал текст в гробнице, правда не все иероглифы в этом тексте были привычными. Многие из них были заменены на шифр «Скиталла». «Скиталла»-это шифр Древней Спарты. Между прочим он является одним из более старинных устройств криптографии. Это устройство так же использовалось в войне между Спартой и Афинами. Но как же оно выглядело и в чем состаяла его судь? Оно представляло собой длинный стержень (карандаш, палку) на который наматывали пергаментовую ленту(собственно шифр). Но самое интересное, что текст наносился на ленту в начале с одной стороны сверху вниз, а затем уже с другой, Таким образом, когда разматывали ленту не возможно было понять, что зашифрованно на ней!
Я тоже попробовала изготовить «Скиталлу» и вот что у меня получилось:
Я намотала ленточку на карандаш и написала текст,
размотала и вправду я не могла понять что там было написано!!!
Итак, о изобретателе шифров я рассказала, кто же первый разгадал их?. .
.
Считается, что это был Аристотель, однако исторического подтверждения этому нет. Аристотель вместо стержня предложил использовать конус и передвигать витки ленты до тех пор пока текст не начнет читаться. Таким образом Аристотель якобы сумел разгадать головоломку, а может про конус он просто выдумал… Дело в том, что многие люди в том числе и я пытались наматывать ленту на конус и сдвигать витки ленты, но все это бес-по-лез-но!!!
В свою очередь в Древнем Риме активно использовался «шифр Цезаря», когда буквы менялись на другие с заданным сдвигом по алфавиту. Свое название этот шифр получил по имени римского императора Гая Юлия Цезаря, который использовал этот шифр при переписке с Цицероном.
При шифровании исходного текста каждая буква заменялась на другую букву того же алфавита по следующему правилу. Заменяющая буква определялась путем смещения по алфавиту от исходной буквы на определенное количество букв (о каком именно должны знать адресат и зашифрофщик) буду называть колличество буквой К. При достижении конца алфавита выполнялся цикличный переход к его началу. Цезарь использовал шифр замены при смещении К = 3. Такой шифр замены можно задать таблицей подстановки, содержащей соответствующие пары букв открытого текста и шифртекста. Совокупность возможных подстановок для К=3 показана в таблице.
Заменяющая буква определялась путем смещения по алфавиту от исходной буквы на определенное количество букв (о каком именно должны знать адресат и зашифрофщик) буду называть колличество буквой К. При достижении конца алфавита выполнялся цикличный переход к его началу. Цезарь использовал шифр замены при смещении К = 3. Такой шифр замены можно задать таблицей подстановки, содержащей соответствующие пары букв открытого текста и шифртекста. Совокупность возможных подстановок для К=3 показана в таблице.
Таблица замены шифра Цезаря:
Например, послание Цезаря «VENI VIDI VICI» («Пришел, Увидел, Победил») выглядело бы в зашифрованном виде так: «YHQL YLGL YLFL».
Задача № 1
Условие задачи таково:
Буквы в исходном тексте не являются настоящими буквами шифра. Они являются буквами правее настоящих. В нашей задачи они будут сдвинуты на 3.
Они являются буквами правее настоящих. В нашей задачи они будут сдвинуты на 3.
К примеру буква А в шифре буква Г, а буква Г в шифре буква Ё.
Записать слова «шифр» и «криптография» используя этот метод.
Ш И Ф Р К Р И П Т О Г Р А Ф И Я
Ы Л Ч У Н У Л Т Х С Ё У Г Ч Л В
Если бы мы не знали принцип этого шифра, мы бы не смогли понять, что же зашифровано. Но шифр этот придумала не я, а Гай Юлий Цезарь.
С помощью этого шифра он общался с генералами. Но однако этот шифр не часто используется для защиты данных. Его используют лишь для демонстрации, а всё из-за того, что этот шифр легко взламывается!!!
В XV веке математик из Италии Леон Батиста Альберти разработал первую математическую модель криптографии. Он же изобрел первое механическое устройство для шифрования секретных документов. «Диск Альберти» состоял из двух дисков –внешнего неподвижного (на нем были нанесены буквы в алфавитном порядке и цифры 1,2,3,4) и подвижного внутреннего диска, на котором буквы были переставлены. Процесс шифрования заключался в нахождении буквы открытого текста на внешнем диске и замене ее на букву с внутреннего диска, стоящую под ней. После этого внутренний диск сдвигался на одну позицию и шифрование второй буквы производилось уже по новому шифралфавиту.
Он же изобрел первое механическое устройство для шифрования секретных документов. «Диск Альберти» состоял из двух дисков –внешнего неподвижного (на нем были нанесены буквы в алфавитном порядке и цифры 1,2,3,4) и подвижного внутреннего диска, на котором буквы были переставлены. Процесс шифрования заключался в нахождении буквы открытого текста на внешнем диске и замене ее на букву с внутреннего диска, стоящую под ней. После этого внутренний диск сдвигался на одну позицию и шифрование второй буквы производилось уже по новому шифралфавиту.
Ключом данного шифра являлся порядок расположения букв на внутреннем диске и его начальное положение относительно внешнего диска.
На основе этого изобретения действовали все криптографические устройства вплоть до появления компьютеров.
В XVII веке Фрэнсис Бекон создал похожее устройство. В нем каждой букве алфавита соответствовало целых пять вариантов шифровки.
В нем каждой букве алфавита соответствовало целых пять вариантов шифровки.
Тогда же ученый и третий президент США Томас Джефферсон создал цилиндрическую шифровальную машину, которая использовала десятки вариантов кодирования. Это устройство состояло из 25 — 36 вращаемых дисков, закрепленных на общей оси. На каждый диск была нанесена своя (причем перемешанная) алфавитная последовательность.
При шифровании текст разбивался на группы, длина которых соответствовала числу используемых дисков. Каждая группа открытого текста устанавливалась на цилиндре в ряд (в одну строку), а в качестве шифротекста выбирался любой из остальных 25 рядов. Дешифровщик совершал ту же процедуру, но в обратном порядке: на цилиндре поочередно устанавливалась в ряд каждая группа шифротекста, после чего просматривались остальные 25 рядов с целью определить, какой из них содержит открытый текст. Этот тип шифра, в свое время являвшийся одной из лучших криптографических систем, называется мультиплексной системой. Устройства, подобные машине Джефферсона, использовались до конца Второй мировой войны.
Этот тип шифра, в свое время являвшийся одной из лучших криптографических систем, называется мультиплексной системой. Устройства, подобные машине Джефферсона, использовались до конца Второй мировой войны.
А сейчас я продемонстрирую задачу по упрощенному устройству «Диск Альберти»
Задача № 2
Для зашифрования текста использовался вращающийся диск, центр которого находится на оси, закрепленной на неподвижном основании. Диск разделен на 32 равных сектора, в которые в неизвестном порядке вписаны все буквы русского алфавита (по одной в каждый сектор; буквы Е и Ё не различаются. Нужно указать, какой из фрагментов полученного шифртекста мы выберем. Буквы я ввела в произвольном порядке.
1 а р ч Ш у д й х ю ы ж э ц ш
2 п а в т И о г р н е к п л д
3 ж э л ш н Ф к п о т и в и р
4 о л в л у е Р у з л к а ф й
Закодирую слово ШИФР:
1 а р ч ш и ф р й х ю ы ж э ц ш г п т с м ш г л ъ б
2 п а в т н е й р н е к п л д ш ы в у ц й ф я ч и т
3 ж э л ш у д г п о т и в и р о ж э р ф й я д с ъ д
4 о л в л у о к у з л к а ф й д у п к о д у ж н у з ц
Для шифровки я выберу 3 ряд: ШУДГ
Разгадать данный шифр может только человек, у которого на устройстве » Диск Альберти» раскладка букв точно такая же!
А ребусы? Мы решаем их и не догадываемся, что и они шифры!
Задача № 3
Многие знают или когда-либо видели этот ребус, в котором одинаковые цифры представляют одинаковыми буквами, но я прорешаю еще раз.
MATH Что означает математика это хорошо
+ IS
_____
GOOD
В ребусе присутствует лишь одна пара с одинаковыми цифрами, что делает ребус более легким. В данном ребусе невозможно составить сумму цифр разряда единиц, чтобы результат получился двузначным числом. Самый легкий вариант начала решения представить одинаковые буквы — нулями, то есть в разряде сотен и десятков будет круглое число. А дальше все просто: в разряде единиц мы прибавляем к одному однозначному число другое и получаем однозначное число, число не превышающее 10
В разряде десятков числа сумма которых равна 10. А в разряде сотен число, которое в сумме с одним дает 10, то есть 9. В разряде тысяч будет любое неповторяющиеся число, которое в сумме с 1 будет отличительное от всех цифр число.
решение
7942
+ 63
____
8005
Однако не думаем же мы, что шифр используется лишь современным человеком? Один из примеров — это использование шифров для защиты нашей страны во время Великой Отечественной войны. Это были не пароли на телефоне или банковских картах, это была — АЗБУКА МОРЗЕ
Азбука Морзе, а точнее » Морзянка» ( азбукой Морзе она начала называться с начала Первой Мировой Войны) — это устройство знаковой зашифровки. Азбука морзе, она же телеграфная азбука – это система кодирования, с помощью которой можно передавать текстовые сообщения в виде последовательности коротких и долгих звуковых сигналов, называемых «точками» и «тире».
Принцип передачи сообщений очень простой: каждому знаку (цифре букве, или знаку препинания) соответствует определенная последовательность точек и тире, которая используется для кодирования текстовых сообщений и последующего их раскодирования. Например, букве «А» соответствует код Морзе, который состоит из короткого и длинного сигнала « », а букве «б» соответствует код Морзе, состоящий из длинного и трех коротких сигналов « »
В азбуке представлены все символы, такие как: цифры, буквы, знаки препинания последовательностью троичных сигналов. Допустим длинных и коротких тире и точек. А придумал эту зашифровку Самюэл Финли Бриз Морзе(1791-1872), собственно поэтому азбука и есть Морзе. Три года он самостоятельно пытался изготовить такую систему, но не получалось
Но на этом старания Морзе не закончились, в 1835 году он стал профессором живописи в только что открытом Нью-Йоркском университете. В этом же университете через два года он и продемонстрировал своё устройство. Морзе удалось построить его. Сигнал был послан по проволке длиной 1700 футов. Но самое интересное, что приемную часть аппарата он изготовил, как подставку для мольберта!!! Крупный американский промышленник Стив Вейл заинтересовался работой Морзе и согласился выделить на разработку 2 тысячи долларов.Он так же предоставил условие для проекта, но лишь при одном условии — Морзе должен был взять к себе в помощники его сына Альфреда. Именно Альфред включил в азбуку буквенные символы. Вариантом азбуки Морзе радисты пользуются до сих пор.
В этом же университете через два года он и продемонстрировал своё устройство. Морзе удалось построить его. Сигнал был послан по проволке длиной 1700 футов. Но самое интересное, что приемную часть аппарата он изготовил, как подставку для мольберта!!! Крупный американский промышленник Стив Вейл заинтересовался работой Морзе и согласился выделить на разработку 2 тысячи долларов.Он так же предоставил условие для проекта, но лишь при одном условии — Морзе должен был взять к себе в помощники его сына Альфреда. Именно Альфред включил в азбуку буквенные символы. Вариантом азбуки Морзе радисты пользуются до сих пор.
Азбуку Морзе я пока не выучила, но в будущем уверена займусь этим.
Заключение.
В заключение хотела бы сказать, что работая над этой исследовательской работой я поняла, что информация сегодня является, скорее всего, самым ценным товаром. Странно, но при этом она остается чуть ли не самой незащищенной для правонарушителей. Криптография старается сберечь информацию столько же, сколько существует наша цивилизация; криптоанализ в то же время пытается эту защиту разрушить. И у обеих сторон есть достижения. И мне все это очень понравилось! В будущем мне кажется я продолжу изучать криптографию. И попробую применить метод зашифровки Цезаря в обычной современной жизни. Азбука Морзе для меня пока сложна, и кто же разгадал метод » Скиталлы»? Ведь доказательств, что это сделал Аристотель НЕТ. А жизни без паролей на телефоне и банковских картах люди нашей планеты себя уже и не представляют! Вот насколько важная эта наука — криптография!
Странно, но при этом она остается чуть ли не самой незащищенной для правонарушителей. Криптография старается сберечь информацию столько же, сколько существует наша цивилизация; криптоанализ в то же время пытается эту защиту разрушить. И у обеих сторон есть достижения. И мне все это очень понравилось! В будущем мне кажется я продолжу изучать криптографию. И попробую применить метод зашифровки Цезаря в обычной современной жизни. Азбука Морзе для меня пока сложна, и кто же разгадал метод » Скиталлы»? Ведь доказательств, что это сделал Аристотель НЕТ. А жизни без паролей на телефоне и банковских картах люди нашей планеты себя уже и не представляют! Вот насколько важная эта наука — криптография!
Спасибо за внимание!
Список литературы.
1.Современная криптография. Теория и практика. Венбо Мао.
2. Алферов, Зубов, Кузьмин, Черемушкин. Основы криптографии. 2005 год.
3.Осипян В.О.Криптография в задачах и упражнениях. 2004 год.
4.Введение в криптографию. Под редакцией В. В. Ященко.
Просмотров работы: 156
Задачи
Задачи по математике и криптографии
В этом разделе содержится архив задач олимпиады, классифицированный по годам и тематике. При этом из серий задач, предлагавшихся в нескольких модификациях для разных возрастных категорий участников, приводится только по одному примеру. С полными комплектами задач, предлагавшихся в конкретном году участникам каждой возрастной категории, можно ознакомиться в разделе Подготовка к олимпиаде.
Год | Все1991/921992/931993/941994/951995/961996/971997/981998/991999/002000/012001/022002/032003/042004/052005/062006/072007/082008/092009/102010/112011/122012/132013/142014/152015/162016/172017/182018/192019/20 |
Рубрики | Все8-9 класс10 класс11 классЗаменыПерестановкиГаммаПротоколыДвоичные системыПереборУравнения и неравенства с параметрамиЛингвистикаГруппа подстановокДелимость. |
Развитие с оглядкой на 9 колен назад, 11 класс
Звуковой барабан, 11 класс
Чтение 32-ичной записки, 11 класс
Ключи в виде уравнений для четверых, 11 кл.
Замены после расширения сообщения, 11 кл.
Три простых числа, 11 кл.
Ключи в виде уравнений для четверых, 10 кл.
Замены после расширения сообщения, 10 кл.
Наложение квадратной гаммы, 10 кл.
Ключ в виде таблицы 7×7, 10 кл.
Страницы:
1
2
3
4
5
6
7
8
9
10
11
…
23
След.
Все
как работают самые известные шифры в истории? — «Хакер»
Содержание статьи
Архаичные шифраторы канули в Лету, чего нельзя сказать об алгоритмах шифрования. Операции сдвига, замены и перестановки до сих пор применяются в современных алгоритмах, однако с существенной поправкой в стойкости. За многие столетия, прошедшие со времен первого применения этих шифров, криптографы научились оценивать количество информации, энтропию и стойкость, однако так было не всегда. Рассмотрим подробнее, как работают самые популярные шифры в истории криптографии и в чем их недостатки.
Roadmap
Это первый урок из цикла «Погружение в крипту». Все уроки цикла в хронологическом порядке:
- Урок 1. Исторические шифры. Основы и исторические шифраторы. Как работают (и анализируются) шифры сдвига, замены, Рихарда Зорге, шифр Вернама и шифровальные машины (ты здесь)
- Урок 2.
 Распределение ключей. Что это такое, как выполняется распределение ключей и как выбрать криптостойкий ключ
Распределение ключей. Что это такое, как выполняется распределение ключей и как выбрать криптостойкий ключ - Урок 3. Современные отечественные шифры. Что такое сеть Фейстеля и какими бывают отечественные блочные шифры, используемые в современных протоколах, — ГОСТ 28147—89, «Кузнечик»
- Урок 4. Современные зарубежные шифры. В чем разница между 3DES, AES, Blowfish, IDEA, Threefish от Брюса Шнайера и как они работают
- Урок 5. Электронная подпись. Виды электронных подписей, как они работают и как их использовать
- Урок 6. Квантовая криптография. Что это такое, где используется и как помогает в распределении секретных ключей, генерации случайных чисел и электронной подписи
В современном обществе, где почти каждый человек имеет электронный девайс (а то и не один), где каждую минуту совершаются операции с электронной валютой, пересылаются конфиденциальные email, подписываются электронные документы, криптография нужна как воздух. Нужна пользователям, чтобы защитить свою приватность. Нужна программистам, чтобы обеспечить безопасность проектируемых систем. Нужна хакерам, чтобы при аудите понимать уязвимые места в системах. Нужна админам, чтобы представлять, чем и как лучше защищать корпоративные данные. Мы не могли обойти стороной такую важную тему и начинаем цикл статей, посвященный введению в криптографию. Для новичков — самый простой путь познакомиться с криптой, для профи — хороший повод систематизировать свои знания. Шесть уроков, от самого простого к сложному. Вперед!
Нужна пользователям, чтобы защитить свою приватность. Нужна программистам, чтобы обеспечить безопасность проектируемых систем. Нужна хакерам, чтобы при аудите понимать уязвимые места в системах. Нужна админам, чтобы представлять, чем и как лучше защищать корпоративные данные. Мы не могли обойти стороной такую важную тему и начинаем цикл статей, посвященный введению в криптографию. Для новичков — самый простой путь познакомиться с криптой, для профи — хороший повод систематизировать свои знания. Шесть уроков, от самого простого к сложному. Вперед!
Термины
Для начала давай определимся с терминологией:
- Криптография — это наука о том, как обеспечить секретность сообщения.
- Криптоанализ — это наука о том, как вскрыть зашифрованное сообщение, не зная ключа.
- Дешифровка — это процесс получения открытого текста средствами криптоанализа.
- Расшифрование — это процесс получения открытого текста с использованием ключа и алгоритма расшифрования, предусмотренного для данного шифра.

В мире криптографии путаться в этих словах — ужасный моветон.
Зачем мне знания о криптографии?
Предположим, криптография очень нужна, но пусть ей займутся дядьки с усами математики. Зачем же мне знания по криптографии?
Если ты обычный пользователь — то как минимум, чтобы обеспечить свою приватность. Сегодня крупным государствам и влиятельным организациям становятся доступны средства тотального надзора за миллионами людей. Поэтому криптография оказывается важнейшим инструментом, обеспечивающим конфиденциальность, доверие, целостность, авторизацию сообщений и электронных платежей. Повсеместное распространение криптографии останется одним из немногих способов защитить пользователя от угроз, нависающих над его конфиденциальной информацией. Зная, как работает тот или иной протокол или шифр, чем он хорош и где его слабые места, ты сможешь осознанно выбирать инструменты для работы или просто общения в Сети.
Если ты программист или специалист по ИБ, то здесь вообще от криптографии никуда не скрыться. Любой крупный проект требует обеспечения безопасности информации. Неважно, что ты разрабатываешь: контентный сервис, почтовик, мессенджер, соцсеть или просто интернет-магазин, — везде есть критичные данные, которые надо защищать от перехвата или угона БД. Каждая операция должна быть защищена криптографическими протоколами. В этом случае криптография — подходящий инструмент. Если ты еще с ней не столкнулся, будь уверен — это на 100% лишь вопрос времени.
Любой крупный проект требует обеспечения безопасности информации. Неважно, что ты разрабатываешь: контентный сервис, почтовик, мессенджер, соцсеть или просто интернет-магазин, — везде есть критичные данные, которые надо защищать от перехвата или угона БД. Каждая операция должна быть защищена криптографическими протоколами. В этом случае криптография — подходящий инструмент. Если ты еще с ней не столкнулся, будь уверен — это на 100% лишь вопрос времени.
Короче говоря, криптография используется гораздо чаще, чем можно себе представить. Поэтому пора снять завесу тайны с этой науки, познакомиться с наиболее интересными аспектами и использовать ее возможности себе на пользу.
Зачем изучать старые шифры?
В интернете криптографические протоколы используются практически при каждом запросе. Но как же дело обстояло, когда интернета не было и в помине? Не стоит думать, что в те далекие лохматые времена не было криптографии. Первые способы шифрования появились около четырех тысяч лет назад. Конечно, это были самые примитивные и нестойкие шифры, однако и население тогда было малограмотное, так что такие способы могли защитить информацию от любопытных глаз.
Конечно, это были самые примитивные и нестойкие шифры, однако и население тогда было малограмотное, так что такие способы могли защитить информацию от любопытных глаз.
Люди всегда нуждались в секретной переписке, поэтому шифрование не стояло на месте. С раскрытием одних шифров придумывали другие, более стойкие. На смену бумажным шифрам пришли шифровальные машины, которым не было равных среди людей. Даже опытному математику не удавалось взломать шифр, рассчитанный на роторной машине. С появлением первых компьютеров требования к защите информации возросли многократно.
Зачем же нам знакомиться с такими древними и нестойкими шифрами, если можно сразу прочитать про DES и RSA — и вуаля, почти специалист? Изучение первых шифров поможет лучше понять, зачем нужна та или иная операция в современном алгоритме шифрования. Например, шифр перестановки, один из первых примитивных алгоритмов, не был забыт, и перестановка — одна из часто встречающихся операций в современном шифровании. Таким образом, чтобы лучше осознать, откуда на самом деле растут ноги у современных алгоритмов, нужно оглянуться на несколько тысяч лет назад.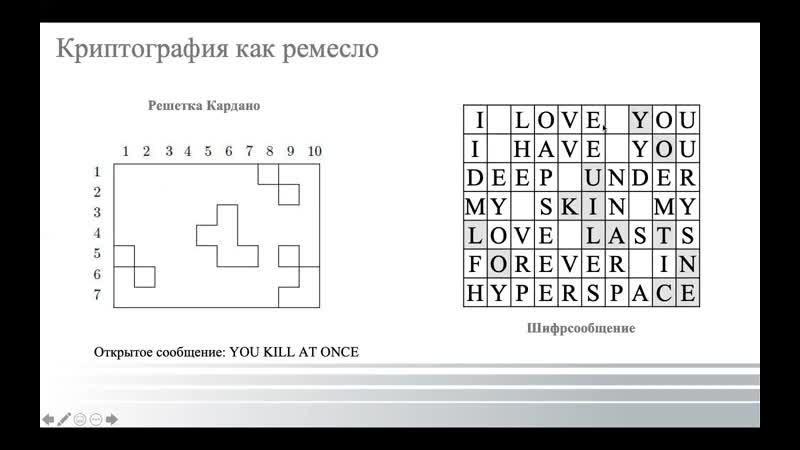
Исторические шифры и первые шифраторы
Согласно источникам, первые способы шифрования текста появились вместе с зарождением письменности. Способы тайного письма применялись древними цивилизациями Индии, Месопотамии и Египта. В письменах Древней Индии упоминаются способы изменения текста, которые использовали не только правители, но и ремесленники, желающие скрыть секрет мастерства. Истоком криптографии считается использование специальных иероглифов в древнеегипетской письменности около четырех тысячелетий назад.
Первым шифром, зародившимся в древних цивилизациях и актуальным, в некотором роде, и по сей день, можно считать шифр замены. Чуть позже был придуман шифр сдвига, который применялся Юлием Цезарем, почему и был назван в его честь.
Помимо шифров, нельзя не упомянуть о приборах для шифрования, которые разрабатывали древние математики. Например, скитала — первый шифратор, разработанный в Спарте. Представлял собой палку, на которую по всей длине наматывалась лента пергамента. Текст наносился вдоль оси палки, после чего пергамент снимался, и получалось шифрованное сообщение. Ключом служил диаметр палки. Однако такой способ шифрования был абсолютно нестойким — автором взлома стал Аристотель. Он наматывал ленту пергамента на конусообразную палку до тех пор, пока не появлялись отрывки читаемого текста.
Текст наносился вдоль оси палки, после чего пергамент снимался, и получалось шифрованное сообщение. Ключом служил диаметр палки. Однако такой способ шифрования был абсолютно нестойким — автором взлома стал Аристотель. Он наматывал ленту пергамента на конусообразную палку до тех пор, пока не появлялись отрывки читаемого текста.
Также ярким примером из мира древних шифраторов может стать диск Энея — диск с отверстиями по количеству букв в алфавите. Нитка протягивалась последовательно в те отверстия, которые соответствовали буквам сообщения. Получатель вытаскивал нитку, записывал последовательность букв и читал секретное послание. Однако этот шифратор обладал существенным недостатком — достать нитку и разгадать послание мог кто угодно.
Шифр сдвига
Это один из самых первых типов шифра. Процесс шифрования очень прост. Он заключается в замене каждой буквы исходного сообщения на другую, отстоящую от исходной на заданное количество позиций в алфавите. Это количество позиций называется ключом. При ключе, равном трем, этот метод называется шифром Цезаря. Император использовал его для секретной переписки. Для того чтобы зашифровать сообщение, нужно построить таблицу подстановок:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c |
Как видишь, во втором ряду символы алфавита сдвинуты на три позиции «назад». Чтобы зашифровать сообщение, для каждого символа исходного текста нужно взять соответствующий ему символ из таблицы подстановки.
Пример шифра
Исходный текст: Hi, Brut! How are you?
Шифрованный текст: Kl, Euxw! Krz duh brx?
Расшифрование
На этапе расшифрования мы имеем шифрованный текст и ключ, равный трем. Чтобы получить исходный текст, ищем для каждого символа сдвиг на три позиции к началу алфавита. Так, для первого символа K сдвиг три будет означать символ H. Далее посимвольно расшифровываем текст, пока не получаем исходную фразу Hi, Brut! How are you?.
Криптоанализ
Легче всего такой шифр взломать простым перебором всех возможных значений ключа — их всего 25. Здесь все просто, и останавливаться смысла нет.
Другой вариант — использовать частотный анализ текста. Для каждого языка есть статистическая информация о частоте употребления каждой буквы алфавита и наиболее часто встречающихся сочетаний букв. Для английского, например, среднестатистические частоты употребления букв таковы:
| e 0,12702 | s 0,06327 | u 0,02758 | p 0,01929 | q 0,00095 |
| t 0,09056 | h 0,06094 | m 0,02406 | b 0,01492 | z 0,00074 |
| a 0,08167 | r 0,05987 | w 0,02360 | v 0,00978 | |
| o 0,07507 | d 0,04253 | f 0,02228 | k 0,00772 | |
| i 0,06966 | l 0,04025 | g 0,02015 | j 0,00153 | |
| n 0,06749 | c 0,02782 | y 0,01974 | x 0,00150 |
Что касается двухбуквенных сочетаний (биграмм), то можно заметить следующую тенденцию:
| Биграмма | Процентное содержание | Биграмма | Процентное содержание |
|---|---|---|---|
| th | 3,15 | he | 2,51 |
| an | 1,72 | in | 1,69 |
| er | 1,54 | re | 1,48 |
| es | 1,45 | on | 1,45 |
| ea | 1,31 | ti | 1,28 |
| at | 1,24 | st | 1,21 |
| en | 1,20 | nd | 1,18 |
Идея в том, что в зашифрованном тексте самой часто встречаемой буквой будет не эталонная e, а что-то другое. Соответственно, нам нужно найти самую часто встречаемую букву в нашем шифре. Это и будет зашифрованная е. А дальше нужно подсчитать ее сдвиг от е в таблице подстановок. Полученное значение и есть наш ключ!
Шифр замены
Основной недостаток шифра сдвига заключается в том, что есть всего 25 возможных значений ключа. Даже Цезарь начал подозревать, что его шифр не самая лучшая идея. Поэтому на смену ему пришел шифр замены. Для того чтобы воспользоваться этим алгоритмом, создается таблица с исходным алфавитом и, непосредственно под ним, тот же алфавит, но с переставленными буквами (или любой другой набор знаков):
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b | e | x | g | w | i | q | v | l | o | u | m | p | j | r | s | t | n | k | h | f | y | z | a | d | c |
Пример шифра
Действуем аналогично предыдущему шифру. Для каждого символа исходного текста берем соответствующий ему из таблицы подстановки:
Исходный текст: Hi, Brut! How are you?
Шифрованный текст: Vl, Enfh!Vrz bnw drf?
Расшифрование
При расшифровании заменяем каждый символ шифротекста соответствующим символом из известной нам таблицы подстановки: v => h, l => i и так далее. После чего получаем исходную строку Hi, Brut! How are you?.
Криптоанализ
Криптоанализ этого шифра также выполняется методом частотного анализа текста. Рассмотрим пример:
MRJGRJ LK HVW XBSLHBM RI QNWBH ENLHBLJ, LHK SRMLHLXBM, WXRJRPLX, BJG XRPPWNXLBM XWJHNW. LH LK RJW RI HVW MBNQWKH XLHLWK LJ HVW ZRNMG BJG HVW MBNQWKH XLHD LJ WFNRSW. LHK SRSFMBHLRJ LK BERFH 8 PLMMLRJ. MRJGRJ LK GLYLGWG LJHR KWYWNBM SBNHK: HVW XLHD, ZWKHPLJKHWN, HVW ZWKH WJG, BJG HVW WBKH WJG. HVW VWBNH RI MRJGRJ LK HVW XLHD, LHK ILJBJXLBM BJG EFKLJWKK XWJHNW. JFPWNRFK EBJUK, RIILXWK, BJG ILNPK BNW KLHFBHWG HVWNW, LJXMFGLJQ HVW EBJU RI WJQMBJG, HVW KHRXU WAXVBJQW, BJG HVW RMG EBLMWD. IWZ SWRSMW MLYW VWNW, EFH RYWN B PLMMLRJ SWRSMW XRPW HR HVW XLHD HR ZRNU. HVWNW BNW KRPW IBPRFK BJXLWJH EFLMGLJQK ZLHVLJ HVW XLHD. SWNVBSK HVW PRKH KHNLULJQ RI HVWP LK HVW KH. SBFM\'K XBHVWGNBM, HVW QNWBHWKH RI WJQMLKV XVFNXVWK. LH ZBK EFLMH LJ HVW 17HV XWJHFND ED KLN XVNLKHRSVWN ZNWJ. HVW HRZWN RI MRJGRJ ZBK IRFJGWG ED OFMLFK XBWKBN BJG LJ 1066 NWEFLMH ED ZLMMLBP HVW XRJTFWNRN. LH ZBK FKWG BK B IRNHNWKK, B NRDBM SBMBXW, BJG B SNLKRJ. JRZ LH LK B PFKWFP.
Частотный анализ букв этого шифра показывает следующее (читай построчно, буквы сортированы по частоте использования):
W — 88, H — 74, L — 67, J — 55, B — 54, K — 52,
R — 51, N — 41, M — 36, V — 35, X — 29, G — 27,
F — 23, P — 16, S — 16, I — 15, Z — 13, E — 13,
D — 11, Q — 10, U — 5, Y — 4, T — 1, O — 1,
A — 1Вероятно, что W => e, так как это самая часто встречающаяся буква в шифре (смотри таблицу среднестатистических частот использования букв для английского языка в предыдущем шифре).
Дальше пробуем найти наиболее короткое слово, куда входит уже известная нам буква W => e. Видим, что сочетание HVW чаще всего встречается в шифре. Нетрудно догадаться, что, скорее всего, это триграмма the, то есть в тексте мы уже определили три символа. Если посмотреть на промежуточный результат, сомнений не остается:
MRJGRJ LK the XBSLtBM RI QNeBt ENLtBLJ, LtK SRMLtLXBM, eXRJRPLX, BJG XRPPeNXLBM XeJtNe. Lt LK RJe RI the MBNQeKt XLtLeK LJ the ZRNMG BJG the MBNQeKt XLtD LJ eFNRSe. LtK SRSFMBtLRJ LK BERFt 8 PLMMLRJ. MRJGRJ LK GLYLGeG LJtR KeYeNBM SBNtK: the XLtD, ZeKtPLJKteN, the ZeKt eJG, BJG the eBKt eJG. the heBNt RI MRJGRJ LK the XLtD, LtK ILJBJXLBM BJG EFKLJeKK XeJtNe. JFPeNRFK EBJUK, RIILXeK, BJG ILNPK BNe KLtFBteG theNe, LJXMFGLJQ the EBJU RI eJQMBJG, the KtRXU eAXhBJQe, BJG the RMG EBLMeD. IeZ SeRSMe MLYe heNe, EFt RYeN B PLMMLRJ SeRSMe XRPe tR the XLtD tR ZRNU. theNe BNe KRPe IBPRFK BJXLeJt EFLMGLJQK ZLthLJ the XLtD. SeNhBSK the PRKt KtNLULJQ RI theP LK the Kt. SBFM\'K XBtheGNBM, the QNeBteKt RI eJQMLKh XhFNXheK. Lt ZBK EFLMt LJ the 17th XeJtFND ED KLN XhNLKtRSheN ZNeJ. the tRZeN RI MRJGRJ ZBK IRFJGeG ED OFMLFK XBeKBN BJG LJ 1066 NeEFLMt ED ZLMMLBP the XRJTFeNRN. Lt ZBK FKeG BK B IRNtNeKK, B NRDBM SBMBXe, BJG B SNLKRJ. JRZ Lt LK B PFKeFP.
Отлично, уже известны три буквы. Снова ищем наиболее короткие слова с новыми известными нам подстановками. Сочетание it является частоупотребляемым, и, поскольку буква t уже дешифрована (HVW => the), очевидно, что в нашем тексте L => i (LH => it). После этого обращаемся к поиску биграмм is и to, устанавливаем, что K => s, R => o. Затем обращаем внимание на триграммы ~ing и and. Анализ текста показывает, что BJG, скорее всего, шифротекст от and. После замены всех наиболее часто встречающихся символов получаем текст:
Mondon is the XaSitaM oI QNeat ENitain, its SoMitiXaM, eXonoPiX, and XoPPeNXiaM XentNe. it is one oI the MaNQest Xities in the ZoNMd and the MaNQest XitD in eFNoSe. its SoSFMation is aEoFt 8 PiMMion. Mondon is diYided into seYeNaM SaNts: the XitD, ZestPinsteN, the Zest end, and the east end. the heaNt oI Mondon is the XitD, its IinanXiaM and EFsiness XentNe. nFPeNoFs EanUs, oIIiXes, and IiNPs aNe sitFated theNe, inXMFdinQ the EanU oI enQMand, the stoXU eAXhanQe, and the oMd EaiMeD. IeZ SeoSMe MiYe heNe, EFt oYeN a PiMMion SeoSMe XoPe to the XitD to ZoNU. theNe aNe soPe IaPoFs anXient EFiMdinQs Zithin the XitD. SeNhaSs the Post stNiUinQ oI theP is the st. SaFM\'s XathedNaM, the QNeatest oI enQMish XhFNXhes. it Zas EFiMt in the 17th XentFND ED siN XhNistoSheN ZNen. the toZeN oI Mondon Zas IoFnded ED OFMiFs XaesaN and in 1066 NeEFiMt ED ZiMMiaP the XonTFeNoN. it Zas Fsed as a IoNtNess, a NoDaM SaMaXe, and a SN
Криптография
Средства криптографической защиты гостайны до сих пор приравниваются к оружию. Очень немногие страны мира имеют свои криптографические компании, которые делают действительно хорошие средства защиты информации. Даже во многих развитых странах нет такой возможности: там отсутствует школа, которая позволяла бы эти технологии поддерживать и развивать. Россия одна из немногих стран мира, – может быть таких стран пять, или около того, – где все это развито. Причем и в коммерческом, и в государственном секторе есть компании и организации, которые сохранили преемственность школы криптографии с тех времен, когда она только зарождалась.
Алгоритмы шифрования
На сегодняшний день существует масса алгоритмов шифрования, имеющих значительную стойкость перед криптоанализом (криптографическую стойкость). Принято деление алгоритмов шифрования на три группы:
- Симметричные алгоритмы
- Ассиметричные алгоритмы
- Алгоритмы хэш-функций
Симметричные алгоритмы
Симметричное шифрование предусматривает использование одного и того же ключа и для зашифрования, и для расшифрования. К симметричным алгоритмам применяются два основных требования: полная утрата всех статистических закономерностей в объекте шифрования и отсутствие линейности.
Принято разделять симметричные системы на блочные и поточные.
В блочных системах происходит разбиение исходных данных на блоки с последующим преобразованием с помощью ключа.
В поточных системах вырабатывается некая последовательность (выходная гамма), которая в последующем накладывается на само сообщение, и шифрование данных происходит потоком по мере генерирования гаммы.
Схема связи с использованием симметричной криптосистемы представлена на рисунке.
Схема связи с использованием симметричной криптосистемы
Где где М — открытый текст, К — секретный ключ, передаваемый по закрытому каналу, Еn(М) — операция зашифрования, а Dk(M) — операция расшифрования
Обычно при симметричном шифровании используется сложная и многоступенчатая комбинация подстановок и перестановок исходных данных, причем ступеней (проходов) может быть множество, при этом каждой из них должен соответствовать «ключ прохода»
Операция подстановки выполняет первое требование, предъявляемое к симметричному шифру, избавляясь от любых статистических данных путем перемешивания битов сообщения по определенному заданному закону. Перестановка необходима для выполнения второго требования – придания алгоритму нелинейности. Достигается это за счет замены определенной части сообщения заданного объема на стандартное значение путем обращения к исходному массиву.
Симметричные системы имеют как свои преимущества, так и недостатки перед асимметричными.
К преимуществам симметричных шифров относят высокую скорость шифрования, меньшую необходимую длину ключа при аналогичной стойкости, большую изученность и простоту реализации.
Недостатками симметричных алгоритмов считают в первую очередь сложность обмена ключами ввиду большой вероятности нарушения секретности ключа при обмене, который необходим, и сложность управления ключами в большой сети.
Примеры симметричных шифров
- ГОСТ 28147-89 — отечественный стандарт шифрования
- 3DES (Triple-DES, тройной DES)
- RC6 (Шифр Ривеста )
- Twofish
- SEED — корейский стандарт шифрования
- Camellia – японский стандарт шифрования
- CAST (по инициалам разработчиков Carlisle Adams и Stafford Tavares)
- IDEA
- XTEA — наиболее простой в реализации алгоритм
- AES – американский стандарт шифрования
- DES – стандарт шифрования данных в США до AES
Асимметричные алгоритмы
Ассиметричные системы также называют криптосистемами с открытым ключом. Это такой способ шифрования данных, при котором открытый ключ передается по открытому каналу (не скрывается) и используется для проверки электронной подписи и для шифрования данных. Для дешифровки же и создания электронной подписи используется второй ключ, секретный.
Само устройство асимметричных криптосистем использует идею односторонних функций ƒ(х), в которых несложно найти х, зная значение самой функции но почти невозможно найти саму ƒ(х), зная только значение х. Примером такой функции может служить телефонный справочник большого города, в котором легко найти номер человека, зная его фамилию и инициалы, но крайне сложно, зная номер, вычислить владельца.
Принцип работы асимметричных систем
Допустим, имеются два абонента: А и В, и абонент В хочет отправить шифрованное сообщение абоненту А. Он зашифровывает сообщение с помощью открытого ключа и передает его уже зашифрованным по открытому каналу связи. Получив сообщение, абонент А подвергает его расшифрованию с помощью секретного ключа и читает.
Схема работы в асимметричной сети
Здесь необходимо сделать уточнение. При получении сообщения абонент А должен аутентифицировать свою личность перед абонентом В для того, чтобы недоброжелатель не смог выдать себя за абонента А и подменить его открытый ключ своим.
Примеры асимметричных шрифтов
- RSA (Rivest-Shamir-Adleman, Ривест — Шамир — Адлеман)
- DSA (Digital Signature Algorithm)
- Elgamal (Шифросистема Эль-Гамаля)
- Diffie-Hellman (Обмен ключами Диффи — Хелмана)
- ECC (Elliptic Curve Cryptography, криптография эллиптической кривой)
- ГОСТ Р 34.10-2001
- Rabin
- Luc
- McEliece
Хеш-функции
Хешированием (от англ. hash) называется преобразование исходного информационного массива произвольной длины в битовую строку фиксированной длины.
Алгоритмов хеш-функций немало, а различаются они своими характеристиками – криптостойкостью, разрядностью, вычислительной сложностью и т.д.
Нас интересуют криптографически стойкие хеш-функции. К таким обычно предъявляют два требования:
- Для заданного сообщения С практически невозможно подобрать другое сообщение С’ с таким же хешем
- Практически невозможно подобрать пар сообщений (СС’), имеющих одинаковый хеш.
Требования называются стойкостью к коллизиям первого рода и второго рода соответственно.
Для таких функций остается важным и другое требование: при незначительном изменении аргумента должно происходить значительное изменение самой функции. Таким образом, значение хеша не должно давать информации даже об отдельных битах аргумента.
Примеры хеш-алгоритмов
- Adler-32
- CRC
- SHA-1
- SHA-2 (SHA-224, SHA-256, SHA-384, SHA-512)
- HAVAL
- MD2
- MD4
- MD5
- N-Hash
- RIPEMD-256
- RIPEMD-320
- Skein
- Snefru
- Tiger (TTH)
- Whirlpool
- ГОСТ Р34.11-94 (ГОСТ 34.311-95)
- IP Internet Checksum (RFC 1071)
Криптографические примитивы
Для придания зашифрованной информации большей криптографической стойкости, в криптографической системе могут многократно применяться относительно простые преобразования – примитивы. В качестве примитивов могут использоваться подстановки, перестановки, циклический сдвиг или гаммирование.
Квантовая криптография
Квантовая криптография по праву считается новым витком в эволюции информационной защиты. Именно она позволяет создать практически абсолютную защиту шифрованных данных от взлома. Идея использовать квантовые объекты для защиты информации от подделки и несанкционированного доступа впервые была высказана Стефаном Вейснером в 1970 г. Спустя 10 лет ученые Беннет и Брассард, которые были знакомы с работой Вейснера, предложили использовать квантовые объекты для передачи секретного ключа. Читать статью «Квантовая криптография (шифрование)»
Криптография в цифровых технологиях
Криптография в цифровых технологиях необходима как инструмент защиты конфиденциальных данных а так же как средство противодействия незаконному копированию и распространению данных, являющихся интеллектуальной собственностью. Читать статью «Криптография в цифровых технологиях»
История
Немецкая шифровальная машина «Enigma» времен 2-й мировой войны в действии
Криптография является древнейшей наукой, и первоначальными ее объектами были текстовые сообщения, которые с помощью определенных алгоритмов лишались смысла для всех, не обладающих специальным знанием по дешифровке этого сообщения – ключом.
Изначально использовались методы, сегодня применяемые разве что для головоломок, то есть, на взгляд современника, простейшие. К таким способам шифрования относятся, например, метод замены, когда каждая буква заменяется другой, отстоящей от нее на строго определенном расстоянии в алфавите. Или метод перестановочного шифрования, когда буквы меняют местами в определенной последовательности внутри слова.
В древние времена шифрование применялось главным образом в военном и торговом деле, шпионаже, среди контрабандистов.
Несколько позже ученые-историки определяют дату появления другой родственной науки – стеганография. Эта наука занимается маскировкой самого факта передачи сообщения. Зародилась она в античности, а примером здесь может служить получение спартанским царем Леонидом перед битвой с персами провощенной дощечки с текстом, покрытой сухим легкосмываемым раствором. При очистке оставленные на воске стилусом знаки становились отчетливо видимыми. Сегодня для сокрытия сообщения служат симпатические чернила, микроточки, микропленки и т.д.
С развитием математики стали появляться математические алгоритмы шифрования, но все эти виды криптографической защиты информации сохраняли в разной объемной степени статистические данные и оставались уязвимыми. Уязвимость стала особенно ощутима с изобретением частотного анализа, который был разработан в IX веке нашей эры предположительно арабским энциклопедистом ал-Кинди. И только в XV веке, после изобретения полиалфавитных шрифтов Леоном Баттистой Альберти (предположительно), защита перешла на качественно новый уровень. Однако в середине XVII века Чарлз Бэббидж представил убедительные доказательства частичной уязвимости полиалфавитных шрифтов перед частотным анализом.
Развитие механики позволило создавать приборы и механизмы, облегчающие шифрование – появились такие устройства, как квадратная доска Тритемиуса, дисковый шифр Томаса Джефферсона. Но все эти приборы ри в какое сравнение не идут с теми, были созданы в XX веке. Именно в это время стали появляться различные шифровальные машины и механизмы высокой сложности, например, роторные машины, самой известной из которых является «Энигма»
До бурного развития науки в XX веке криптографам приходилось иметь дело только с лингвистическими объектами, а в ХХ веке открылись возможности применения различных математических методов и теорий, статистики, комбинаторики, теории чисел и абстракной алгебры.
Но настоящий прорыв в криптографической науке произошел с появлением возможности представления любой информации в бинарном виде, разделенной на биты с помощью компьютеров, что позволило создавать шрифты с доселе невиданной криптографической стойкостью. Такие системы шифрования, конечно, могут быть подвергнуты взлому, но временные затраты на взлом себя в подавляющем большинстве случаев не оправдывают.
Сегодня можно говорить о значительных разработках в квантовой криптографии.
Литература
- Баричев С.Г., Гончаров В.В., Серов Р.Е. Основы современной криптографии. — М.: *Варфоломеев А. А., Жуков А. Е., Пудовкина М. А. Поточные криптосистемы. Основные свойства и методы анализа стойкости. М.: ПАИМС, 2000.
- Ященко В. В. Введение в криптографию. СПб.: Питер, 2001. ISBN 5-318-00443-1.
- ГОСТ 28147-89. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования. М.: ГК СССР по стандартам, 1989.
- ГОСТ Р 34.10-94.Информационная технология. Криптографическая защита информации. *ГОСТ Р 34.11-94. Информационная технология. Криптографическая защита информации. Функция хэширования. М., 1995.
- ГОСТ Р 34.10-2001 Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи. М., 2001.
- Нечаев В. И. Элементы криптографии (Основы теории защиты информации). М.: Высшая школа, 1999.
- Жельников В. Криптография от папируса до компьютера. М.: АВР,1996.
Ссылки
Читайте также
Поручение Владимира Путина о переходе госорганов на использование российских средств шифрования.
Криптография — Википедия
Материал из Википедии — свободной энциклопедии
Криптогра́фия (от др.-греч. κρυπτός «скрытый» + γράφω «пишу») — наука о методах обеспечения конфиденциальности (невозможности прочтения информации посторонним), целостности данных (невозможности незаметного изменения информации), аутентификации (проверки подлинности авторства или иных свойств объекта), а также невозможности отказа от авторства.
Изначально криптография изучала методы шифрования информации — обратимого преобразования открытого (исходного) текста на основе секретного алгоритма или ключа в шифрованный текст (шифротекст). Традиционная криптография образует раздел симметричных криптосистем, в которых зашифровывание и расшифровывание проводится с использованием одного и того же секретного ключа. Помимо этого раздела современная криптография включает в себя асимметричные криптосистемы, системы электронной цифровой подписи (ЭЦП), хеш-функции, управление ключами, получение скрытой информации, квантовую криптографию.
Криптография не занимается защитой от обмана, подкупа или шантажа законных абонентов, кражи ключей и других угроз информации, возникающих в защищённых системах передачи данных.
Криптография — одна из старейших наук, её история насчитывает несколько тысяч лет.
Терминология
- Открытый (исходный) текст — данные (не обязательно текстовые), передаваемые без использования криптографии.
- Шифротекст, шифрованный (закрытый) текст — данные, полученные после применения криптосистемы (обычно — с некоторым указанным ключом).
- Шифр, криптосистема — семейство обратимых преобразований открытого текста в шифрованный.
- Ключ — параметр шифра, определяющий выбор конкретного преобразования данного текста. В современных шифрах криптографическая стойкость шифра целиком определяется секретностью ключа (принцип Керкгоффса).
- Шифрование — процесс нормального применения криптографического преобразования открытого текста на основе алгоритма и ключа, в результате которого возникает шифрованный текст.
- Расшифровывание — процесс нормального применения криптографического преобразования шифрованного текста в открытый.
- Асимметричный шифр, двухключевой шифр, шифр с открытым ключом — шифр, в котором используются два ключа, шифрующий и расшифровывающий. При этом, зная лишь ключ зашифровывания, нельзя расшифровать сообщение, и наоборот.
- Открытый ключ — тот из двух ключей асимметричной системы, который свободно распространяется. Шифрующий для секретной переписки и расшифровывающий — для электронной подписи.
- Секретный ключ, закрытый ключ — тот из двух ключей асимметричной системы, который хранится в секрете.
- Криптоанализ — наука, изучающая математические методы нарушения конфиденциальности и целостности информации.
- Криптоаналитик — учёный, создающий и применяющий методы криптоанализа.
- Криптография и криптоанализ составляют криптологию, как единую науку о создании и взломе шифров (такое деление привнесено с запада, до этого в СССР и России не применялось специального деления).
- Криптографическая атака — попытка криптоаналитика вызвать отклонения в атакуемой защищённой системе обмена информацией. Успешную криптографическую атаку называют взлом или вскрытие.
- Дешифрование (дешифровка) — процесс извлечения открытого текста без знания криптографического ключа на основе известного шифрованного. Термин дешифрование обычно применяют по отношению к процессу криптоанализа шифротекста (криптоанализ сам по себе, вообще говоря, может заключаться и в анализе криптосистемы, а не только зашифрованного ею открытого сообщения).
- Криптографическая стойкость — способность криптографического алгоритма противостоять криптоанализу.
- Имитозащита — защита от навязывания ложной информации. Другими словами, текст остаётся открытым, но появляется возможность проверить, что его не изменяли ни случайно, ни намеренно. Имитозащита достигается обычно за счет включения в пакет передаваемых данных имитовставки.
- Имитовставка — блок информации, применяемый для имитозащиты, зависящий от ключа и данных.
- Электронная цифровая подпись, или электронная подпись — асимметричная имитовставка (ключ защиты отличается от ключа проверки). Другими словами, такая имитовставка, которую проверяющий не может подделать.
- Центр сертификации — сторона, чья честность неоспорима, а открытый ключ широко известен. Электронная подпись центра сертификации подтверждает подлинность открытого ключа.
- Хеш-функция — функция, которая преобразует сообщение произвольной длины в число («свёртку») фиксированной длины. Для криптографической хеш-функции (в отличие от хеш-функции общего назначения) сложно вычислить обратную и даже найти два сообщения с общей хеш-функцией.
История
Использовавшийся в Древней Греции шифр «скитала», чья современная реконструкция показана на фото, вероятно был первым устройством для шифрования
Роторная шифровальная машина Энигма, разные модификации которой использовались немецкими войсками с конца 1920-х годов до конца Второй мировой войны[1]
История криптографии насчитывает около 4 тысяч лет. В качестве основного критерия периодизации криптографии возможно использовать технологические характеристики используемых методов шифрования.
Первый период (приблизительно с 3-го тысячелетия до н. э.) характеризуется господством моноалфавитных шифров (основной принцип — замена алфавита исходного текста другим алфавитом через замену букв другими буквами или символами). Второй период (хронологические рамки — с IX века на Ближнем Востоке (Ал-Кинди) и с XV века в Европе (Леон Баттиста Альберти) — до начала XX века) ознаменовался введением в обиход полиалфавитных шифров. Третий период (с начала и до середины XX века) характеризуется внедрением электромеханических устройств в работу шифровальщиков. При этом продолжалось использование полиалфавитных шифров.
Четвёртый период — с середины до 70-х годов XX века — период перехода к математической криптографии. В работе Шеннона появляются строгие математические определения количества информации, передачи данных, энтропии, функций шифрования. Обязательным этапом создания шифра считается изучение его уязвимости к различным известным атакам — линейному и дифференциальному криптоанализам. Однако, до 1975 года криптография оставалась «классической», или же, более корректно, криптографией с секретным ключом.
Современный период развития криптографии (с конца 1970-х годов по настоящее время) отличается зарождением и развитием нового направления — криптография с открытым ключом. Её появление знаменуется не только новыми техническими возможностями, но и сравнительно широким распространением криптографии для использования частными лицами (в предыдущие эпохи использование криптографии было исключительной прерогативой государства). Правовое регулирование использования криптографии частными лицами в разных странах сильно различа
Современная криптография: наука и искусство
— Современную криптографию уже невозможно представить без математики. Можно об этом рассказать чуть подробнее?
— Активное использование математических методов – это, на мой взгляд, одна из самых сильных сторон отечественной криптографической школы. Дело в том, что с помощью математических методов можно не только сконструировать сложные современные шифры, но и строго обосновать их криптографическую стойкость – способность противостоять практическому или теоретическому взлому – криптоанализу. И это наиболее важное применение математики в криптографии.
Если говорить просто, то задача криптоанализа – это восстановление информации о секретном ключе. Зная ключ, злоумышленник получает возможность проводить дешифрование перехватываемых им сообщений, изменять и подменять их, подписывать чужим именем и т.д. Так вот, современный криптоанализ – он ведь абсолютно математичен. Например, статистические методы анализа шифров, возникшие издавна из простого частотного анализа и заключающиеся в поиске закономерностей в шифртексте, не мыслимы сейчас без результатов математической статистики и разработанных в ней эффективных критериев различения статистических гипотез. Современные аналитические методы криптоанализа, такие как алгебраический криптоанализ, заключаются в описании работы шифра с помощью большой переопределенной системы булевых уравнений, от эффективности решения которой зависит успех криптоаналитика. Значит, нужно учиться решать такие системы уравнений, разрабатывать новые математические методы для этого. Или – криптоанализ систем «нового поколения», так называемых систем с открытым ключом. В таких системах (например, RSA, ElGamal, Shamir и др., активно применяющихся в криптографических протоколах сети Интернет) используются последние достижения теории чисел и алгебры. Взломать их – значит решить сложные математические задачи. Например, изобрести эффективный алгоритм разложения числа на множители, вычисления дискретного логарифма и т.д. То есть, опять – математика. Никак без нее. Правда, не совсем так. Без математики, в общем-то, можно пробовать – но это будут исследования наугад, эксперименты с входными данными и большими вычислительными мощностями (кстати, этот стиль криптографических исследований довольно популярен на Западе). Можно и на этом пути достичь некоторого – временного – успеха, но все значительные теоретические результаты в криптографии и криптоанализе имеют под собой серьезную математическую основу.
Соответственно математичными должны быть и средства, позволяющие противостоять криптоанализу. В этой области возникают такие задачи, как конструирование элементов шифра (например, дискретных функций), обладающих специальными свойствами.
— Криптографию и криптоанализ назвали наиболее важными формами разведки в современном мире. А они сводятся к холодным математическим вычислениям. Кто лучше вычисляет, тот и побеждает. Или есть еще что-то?
— Научные методы криптографии – это методы дискретной математики, алгебры, теории вероятностей, математической статистики. И в то же время криптография – это искусство. Объекты, которые она исследует, могут не подчиняться математическим законам, а научные методы иногда не дают результата. И тогда остается только воображение.
— А можно рассказать о том, какие научные работы в сфере криптографии и криптоанализа ведутся в Институте математики СО РАН?
— Можно было бы сказать, что мы исследуем так называемый шифр Цезаря… и некоторые его модификации. Однако, к счастью, о наших исследованиях можно рассказать и подробнее. В институте математики им. С.Л. Соболева мы, в основном, занимаемся исследованием криптографических свойств булевых функций, использующихся при конструировании шифров. Булева функция отображает n двоичных битов в множество из нуля и единицы. В каком-то смысле это наиболее простые функции. С помощью булевых функций – как составных элементов – строится практически каждый симметричный шифр.
Изучая математические свойства булевых функций, можно оценивать криптографическую стойкость шифров, в которых они используются. Известно много примеров того, как неудачный выбор булевых функций приводил к успешным атакам на шифр, например, на бывший государственный стандарт США блочный шифр DES (1993) и поточный шифр Grain, вошедший в число финалистов международного проекта eCRYPT (2011).
Если интересно, расскажу про DES подробнее. В 1993 году исследователями из Японии была обнаружена существенная слабость к линейному криптоанализу блочного шифра DES. Этот шифр был стандартом симметричного шифрования США на протяжении почти двадцати лет (с 1980 года по 1998 год). Слабость шифра, которая привела к успешной атаке на него, заключалась в отсутствии необходимых криптографических свойств его нелинейных компонент, заданных векторными булевыми функциями. По той же причине шифр оказался нестойким и к дифференциальному криптоанализу. В 1999 году шифр DES потерял статус государственного стандарта. Стойкость шифра к упомянутым методам криптоанализа может быть достигнута за счет использования максимально нелинейных булевых функций и их обобщений при построении S-блоков, что и было сделано в более современных шифрах, таких как шифры AES (современный стандарт США) и CAST (стандарт Канады).
К числу свойств, которые мы изучаем, относятся высокая нелинейность (упрощенно, – способность противостоять линейному криптоанализу), уравновешенность (частотный криптоанализ), большая алгебраическая степень функции, ее алгебраическая и корреляционная иммунность (алгебраический криптоанализ) и другие. Часто криптографические свойства противоречат друг другу, и при выборе булевой функции требуется находить компромисс между различными свойствами. Решение этих задач тесно связано со многими открытыми математическими вопросами дискретной математики, алгебры, теории графов и комбинаторики.
Одно из наших новых направлений – исследование методов защиты шифров от атак по сторонним каналам, от так называемого «нечестного» криптоанализа, который проводится не на основе математической модели шифра (как правило, модель шифра сама по себе не секретна), а на основе «прослушивания» реализации шифра.
Например, если шифр «зашит» в некотором устройстве, то «нечестным» методом его анализа считается тот, который использует данные о возникающем электромагнитном излучении при его работе, о времени вычислений, шуме и другие данные, полученные с установленных снаружи «жучков». Чтобы защитить шифр от подобных атак, необходимо маскировать его структуру. В том числе и булевы функции, описывающие его компоненты. При этом задача маскирования булевых функций хорошо формулируется математически – требуется строить разложения исходной булевой функции в сумму нескольких функций с определенными свойствами, выяснять, когда такие разложения существуют и т.п.
В работе принимают активное участие аспиранты ИМ СО РАН и студенты НГУ. В настоящее время мы проводим совместные научные исследования с лабораторией компьютерной безопасности и криптографии COSIC (Бельгия), широко известной по разработке нескольких мировых криптографических стандартов. Эта лаборатория является одной из наиболее успешных криптографических лабораторий мира. Ее сотрудниками были разработаны современный стандарт блочного шифрования США – шифр AES (2002), а также новая хэш-функция Keccak, ставшая победителем международного конкурса SHA-3 (2012). Стараемся перенимать их опыт.
Кроме научных задач мы занимаемся преподаванием на мехмате НГУ и в физико-математической школе (СУНЦ). Проводим такие курсы, как «Криптография и криптоанализ», «Криптография в задачах» и другие, издаем учебные пособия. В институте математики уже несколько лет проводим научный семинар по криптографии. Наши студенты и аспиранты занимаются подготовкой школьников СУНЦ к Всероссийской олимпиаде по математике и криптографии. Например, в прошлом 2012 году подготовленные ими ученики 11 класса СУНЦ заняли на этой олимпиаде 6 призовых мест по России (к слову, на Новосибирск пришлось всего восемь призовых мест)
— И в заключение, немного о перспективах дальнейшего развития математической криптографии?
— Криптография, конечно, будет активно развиваться. Одна из ее новых задач – разработка скоростных методов шифрования с высоким уровнем секретности. Эта задача обусловлена появлением новых каналов связи (беспроводные сети, сотовая связь, Интернет), по которым передаются всё большие объемы информации. И как бы ни росли со временем вычислительные возможности у криптографов, достигать оптимальной стойкости криптографических систем при ограниченной скорости шифрования можно будет, лишь применяя при их разработке серьезные математические результаты. Как-никак задача нахождения оптимума – это математическая задача. Так было и тысячу лет назад, так будет и в далеком будущем.
В заключение хотелось бы пожелать успешного развития отечественной криптографии. И научной, и практической. Хочется верить, что со временем во многих используемых нами устройствах (компьютерах, сотовых телефонах, охранных системах) наконец-то появятся криптографические протоколы и шифры, разработанные в России. Мы в данном случае говорим о гражданской криптографии, в ее закрытой части Россия, судя по всему, как всегда на мировом уровне. Осталось догнать в том, что можно определить и как гражданскую, и как коммерческую криптографию. Но для этого нужно много работать. Очень много.
Юрий Курьянов
Математика и криптография | GCHQ
Математика и прикладная криптография
Нам необходимо понять, как криптографические технологии используются в повседневной жизни, и проанализировать слабые места на уровне продукта, протокола, системы или оборудования. Мы делаем это, комбинируя идеи из всего математического спектра с широким спектром навыков компьютерной безопасности. Мы особенно заинтересованы в увеличении числа соискателей из математических и компьютерных специальностей, чтобы поддержать эту работу.
Чтобы изучить алгоритмы, лежащие в основе этих технологий, нам необходимо применить ряд криптоаналитических методов, чтобы понять потенциальные недостатки. Это включает в себя привлечение методов из теории вероятностей и статистики, теории групп, комбинаторики и теории сложности, а также энтузиазм в решении проблем, а затем максимально эффективное применение наших идей с использованием некоторых из самых мощных компьютеров в Европе. Наши сильные стороны заключаются в том, что каждый может внести свой вклад в различные области знаний, необходимых для решения наших самых сложных проблем, и мы предлагаем обширное обучение для всех частей нашей работы.
Криптографическая безопасность
Мы разрабатываем криптографию Великобритании и предоставляем консультации по ее применению в государственных системах. Это может включать разработку и реализацию индивидуальных алгоритмов или протоколов для использования в ограниченных или сложных средах или обеспечение безопасности систем, которые потребуют защиты на многие годы в будущем. Нам нужно понимать, как криптографические технологии используются в повседневной жизни, тесно сотрудничая с поставщиками и их продуктами.
Криптография с открытым ключом является краеугольным камнем, на котором построен современный цифровой мир, в то время как следующее поколение криптографии будет иметь в своей основе квантово-устойчивые алгоритмы, разработанные для защиты от атак со стороны гипотетического квантового компьютера. Мы ведем британские исследования в этих областях. Для этого мы должны понимать ряд чисто математических проблем (таких как целочисленная факторизация и вычисление дискретного логарифма), в то время как для оценки новых квантовых протоколов нам необходимо привнести понимание принципов квантовой системной инженерии в наше криптографическое мышление.
Наука о данных и обработка информации
Мы разрабатываем и внедряем современные методы машинного обучения и анализа графиков для обнаружения закономерностей в больших хранилищах данных или больших объемов данных и потоков данных, а также создаем статистические модели для улучшения обработки данных и распознавания образов для разведывательные и кибербезопасные миссии.
Мы получаем данные в различных форматах, часто нераспознаваемых или поврежденных, и нам необходимо понимать эти данные, чтобы мы могли извлечь основную информацию.Для этого типа работы требуется сочетание математического моделирования и готовности генерировать и проверять новые идеи на основе ограниченных знаний.
Благодаря партнерским отношениям между правительством, промышленностью и академическими кругами, включая недавно созданный Институт Алана Тьюринга, GCHQ создает динамичное сообщество специалистов по науке о данных.
Летняя программа по математике и криптографии
GCHQ — один из немногих неакадемических центров, где вы можете использовать, расширять и развивать свои исследовательские навыки в области математики в реальных условиях.Вот почему мы ищем преданных математиков, которые ожидают получения диплома с отличием 1-го класса по математике или совместного диплома с отличием, в котором математика является основным компонентом, которые хотят продолжить передовые математические исследования в своей карьере. Присоединяйтесь к нам в нашей девятинедельной летней программе, и вы сможете вместе с нашими экспертами работать над проблемами, которые имеют действительно практическое значение, в том числе:
- Исследование криптографических алгоритмов;
- Оценка безопасности криптографических приложений и протоколов;
- Разработка новых математических методов и аналитических инструментов;
- Анализ и моделирование сложных наборов данных;
- Реализация и оптимизация сложных математических алгоритмов на высокопроизводительных компьютерах;
- Понимание цифровых сигналов, полученных по зашумленным каналам
Чтобы подать заявку, вам необходимо закончить как минимум три года вашей степени к началу программы и быть на пути к получению квалификации 1-го класса с отличием по математике (бакалавриат, магистр или эквивалент) или предмету с отличием. с математикой в качестве основного компонента.
Математика криптографии, часть I
8 простых чисел и модульная арифметика
8 Простые числа и модульная арифметика 8.1 Простые числа и множители Уже более двух тысячелетий назад люди во всем мире рассматривали свойства чисел.Одно из самых простых понятий — простые числа.
Подробнее
РЕШЕНИЯ ДЛЯ КОМПЛЕКТА ПРОБЛЕМ 2
РЕШЕНИЯ ДЛЯ НАБОРА ЗАДАЧ 2 A: Существуют такие простые числа p, что p + 6k также является простым для k = 1,2 и 3. Одно такое простое число равно p = 11. Другое такое простое число равно p = 41. Докажите, что существует ровно одно простое p такое
Подробнее
Алгоритмы факторинга
Алгоритмы факторинга Метод p 1 и квадратичное решето 17 ноября 2008 г. () Алгоритмы факторинга 17 ноября 2008 г. 1/12 Метод факторинга Ферма Ферма обнаружил, что если n имеет два множителя,
Подробнее
z 0 и y даже имели вид
Гауссовские целые числа. Понятия делимости, простоты и факторизации на самом деле более общие, чем обсуждаемые до сих пор.На данный момент мы работаем с целыми числами, которые обозначим Z
.
Подробнее
Домашнее задание до теста №2
MATh41: Домашнее задание по теории чисел до теста № Филипп БРАУН Раздел 3.1, стр. 43, 1. Было высказано предположение, что существует бесконечно много простых чисел формы n. Покажите пять таких простых чисел. Решение. Пять таких
Подробнее
Арифметика и алгебра матриц
Арифметика и алгебра матриц Math 572: Алгебра для учителей средней школы Университет Монтаны 1 Действительные числа 2 Связь в классе: системы линейных уравнений 3 Рациональные числа 4 Иррациональные
Подробнее
Математический контент по Strand 1
Математическое содержание по числу строк 1 и операции с целыми числами Умножение и деление 3 класс В 3 классе учащиеся изучают свойства умножения и деления, включая обратное
Подробнее
Алгоритмы факторинга
Institutionen för Informationsteknologi Lunds Tekniska Högskola Департамент информационных технологий Лундский университет Криптология — Проект 1 алгоритмов факторинга Цель этого проекта — понять
Подробнее
8 Делимость и простые числа
8 Делимость и простые числа 8.1 Делимость В этом коротком разделе мы расширяем понятие кратного с натуральных чисел до целых. Мы также суммируем несколько других терминов, которые выражают
Подробнее
СУММА ДВУХ КВАДРАТОВ ДЖАХНАВИ БХАСКАР
СУММА ДВУХ КВАДРАТОВ ДЖАХНАВИ БХАСКАР Аннотация. Я исследую, какие числа можно записать как сумму двух квадратов и сколькими способами, предоставив достаточно основ теории чисел, чтобы даже незнакомый
Подробнее
RSA и тестирование на простоту
и проверка на первичность Джоан Бояр, IMADA, Университет Южной Дании Studieretningsprojekter 2010 1/81 Корректность криптографической криптографии Введение в теорию чисел Корректность с 2
Подробнее
Примечания к определителю
ENGG2012B Заметки по высшей инженерной математике по определителю Лектор: Кеннет Шум Лекция 9-18 февраля 2013 г. Определитель системы линейных уравнений определяет, является ли решение уникальным без
Подробнее
MACM 101 Дискретная математика I
MACM 101 Дискретная математика I Упражнения по комбинаторике, теории вероятностей, языкам и целым числам.Срок сдачи: вторник, 2 ноября (в начале занятия). Напоминание: работа, которую вы отправляете, должна быть вашей собственной.
Подробнее
Подобные матрицы и жорданова форма
Подобные матрицы и жорданова форма Мы почти охватили всю основу линейной алгебры, как только мы закончили сингулярные разложения, мы увидим все наиболее важные темы. A T A положительный
Подробнее
Лекция 13 — Основы теории чисел.
Лекция 13 — Основы теории чисел. Боаз Барак 22 марта 2010 г. Делимость и простые числа Если в этой лекции не указано иное, все числа являются целыми неотрицательными числами. Мы говорим, что A делит B, обозначается
Подробнее
Евклидов алгоритм
Алгоритм Евклида МЕТОД НАЙТИ НАИЛУЧШЕГО ОБЩЕГО ДЕЛЕНИЯ ДЛЯ ДВУХ БОЛЬШИХ ЧИСЕЛ Чтобы добиться успеха при использовании этого метода, вы должны знать, как делить.Если это то что у вас
Подробнее
Нули полиномиальной функции
Нули полиномиальной функции Важным следствием теоремы о множителях является то, что нахождение нулей полинома — это то же самое, что разложение его на линейные множители. В этом разделе мы
Подробнее
Группы в криптографии
Группы в криптографии Четин Кая Коч http: // cs.ucsb.edu/~koc/cs178 [email protected] Koç (http://cs.ucsb.edu/~koc) ucsb cs 178 intro to crypto winter 2013 1/13 Группы в криптографии Набор S и двоичный
Подробнее
Имя: Раздел, в котором зарегистрирован:
Имя: Раздел Зарегистрирован в: Математика 125 Экзамен 3 Версия 1 24 апреля 2006 г. Всего возможно 60 баллов 1. (5 баллов) Используйте правило Крамера, чтобы решить 3x + 4y = 30 x 2y = 8. Обязательно покажите достаточно деталей, чтобы показать вам
Подробнее
Глава 11 Теория чисел
Глава 11 Теория чисел Теория чисел — один из старейших разделов математики.Многие годы люди, изучавшие теорию чисел, восхищались ее чистой природой, потому что практических приложений было мало
Подробнее
Раздаточный материал ТЕОРИЯ НОМЕРОВ
Раздаточный материал «Теория чисел» Куса Прихантозо Криснавана ОТДЕЛЕНИЕ МАТЕМАТИКИ ФАКУЛЬТЕТ МАТЕМАТИКИ И ЕСТЕСТВЕННЫХ НАУК ЙОГЬЯКАРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 2012 Содержание Содержание i 1 Некоторые предварительные соображения
Подробнее
Факторинговые полиномы
Факторинг многочленов Сью Геллер 19 июня 2006 г. Факторинг многочленов по рациональным, действительным и комплексным числам долгое время был стандартной темой алгебры старших классов.С появлением
Подробнее
Линейное программирование. 14 марта 2014 г.
Линейное программирование 1 марта 2001 г. Части этого введения в линейное программирование были адаптированы из главы 9 «Введение в алгоритмы», второе издание, Кормена, Лейзерсона, Ривеста и Стейна [1]. 1
Подробнее
Блок 18 Детерминанты
Блок 18 Детерминанты С каждой квадратной матрицей связано число, называемое определителем.В этом разделе мы определим, как вычислить это число, а также рассмотрим некоторые свойства
.
Подробнее
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
ОПРЕДЕЛЕНИЕ: НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ Наибольший общий делитель (НОД) чисел a и b, обозначаемый (a, b), является наибольшим общим делителем целых чисел a и b. ТЕОРЕМА: Если a и b ненулевые целые числа, то их
Подробнее
1 Введение в матрицы
1 Введение в матрицы В этом разделе представлены важные определения и результаты матричной алгебры, которые полезны в регрессионном анализе.Хотя все приведенные ниже утверждения относительно столбцов
Подробнее
Компьютерная и сетевая безопасность
MIT 6.857 Примечания к классу безопасности компьютеров и сети 1 Файл: http://theory.lcs.mit.edu/ rivest / notes / notes.pdf Версия: 2 декабря 2002 г. Компьютерная и сетевая безопасность MIT 6.857 Примечания к классу Рональда Л. Ривеста
Подробнее
СОДЕРЖАНИЕ. Пожалуйста, обратите внимание:
СОДЕРЖАНИЕ Введение…iv. Системы счисления … 2. Алгебраические выражения …. Факторизация … 24 4. Решение линейных уравнений … 8. Решение квадратных уравнений … 0 6. Одновременные уравнения …. Длинное деление
Подробнее
ФАКТОРЫ И МНОЖЕСТВА Ключ ответа
I. Найдите простые множители с помощью метода факторного дерева ФАКТОРЫ И МНОЖЕСТВА Ключевые слова a. 768 2 384 2 192 2 96 2 48 2 24 2 12 2 6 2 3 768 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 б. 1608 3 536 2 268 2 134 2 67 1608 = 3 * 2 * 2 * 2 * 67 c.
Подробнее
Введение в шифр Хилла
Введение в шифр Хилла Мы исследовали три простых подстановочных шифра, которые генерируют зашифрованный текст C из открытого текста p посредством арифметической операции по модулю 26. Шифр Цезаря: шифр Цезаря
Подробнее
Криптография
- Тематический каталог
- Гуманитарные и социальные науки
- Антропология
- Изобразительное искусство
- Каталог коммуникаций, кино и театра
- Массовые коммуникации / Связи с общественностью / Фильм
- Речевое общение
- Театр
- английский
- Сочинение
- Развивающий английский
- Литература и творческое письмо
- Техническая коммуникация
- История
- Междисциплинарные исследования
- Семейные исследования и человеческое развитие
- Гуманитарные науки
- Расовые и этнические исследования
- Социальная наука
- Женские и гендерные исследования
- Музыка
- Гуманитарные и социальные науки
Эллиптическая криптография | плюс.maths.org
Эллиптические кривые — это очень важная новая область математики, которая активно изучалась за последние несколько десятилетий. Они показали огромный потенциал как инструмент для решения сложных числовых задач, а также для использования в криптографии.
В 1994 году Эндрю Уайлс вместе со своим бывшим учеником Ричардом Тейлором решил одну из самых известных математических задач за последние 400 лет, Великую теорему Ферма, используя эллиптические кривые. В последние несколько десятилетий также было проведено много исследований по использованию эллиптических кривых вместо того, что называется шифрованием RSA для обеспечения безопасности передачи данных в Интернете.
Государственные и частные
Maths хранит ваши данные в безопасности.
Криптография на основе эллиптических кривых, как и криптография RSA, является примером криптографии с открытым ключом . Основная идея этого заключается в том, что
замок. Если я хочу послать вам секретное сообщение, я могу попросить вас прислать мне открытый замок, ключ от которого есть только у вас. Затем я кладу свое сообщение в ящик, закрываю его замком и отправляю вам. Преимущество этого подхода в том, что сообщение может быть отправлено по незащищенным каналам — даже если кто-то перехватит ящик, у него нет ключа — и что нам обоим не нужен ключ от ящика.Вы даже можете заставить множество людей отправлять вам секретные сообщения таким образом, даже не отдавая ни единого ключа.
В криптографии с открытым ключом сообщения шифруются с использованием определенных фрагментов математической информации, которые составляют открытый ключ . — это открытый замок, а выполнение шифрования похоже на закрытие замка. Расшифровка возможна только с использованием математического закрытого ключа , который практически невозможно определить, если вы знаете только открытый ключ.
В криптографии RSA открытый ключ включает натуральное число, которое используется компьютерами для шифрования сообщений. Чтобы расшифровать сообщение, вам необходимо знать, что коэффициент If очень велик, то факторинг требует таких больших вычислительных мощностей, что взломать код практически невозможно. Только люди (или, на самом деле, компьютеры), обладающие закрытым ключом — факторами — могут легко расшифровать сообщение. (Вы можете узнать больше об RSA здесь.)
Эллиптические кривые
Криптография с эллиптическими кривыми основана на сложности решения числовых задач, связанных с эллиптическими кривыми.На простом уровне их можно рассматривать как
кривые, заданные уравнениями вида
где и — константы. Ниже приведены некоторые примеры. В каждом случае на графике показаны все точки с координатами, где и удовлетворяют уравнению приведенной выше формы.
Эллиптические кривые, соответствующие целочисленным значениям a между -2 и 1 и целочисленным значениям значений b между -1 и 2.Только кривая для a = b = 0 не квалифицируется как эллиптическая кривая, потому что у нее есть особая точка.
Для точности нам нужно сказать пару слов о константах и Чтобы уравнение приведенной выше формы можно было квалифицировать как эллиптическую кривую, нам нужно, чтобы это обеспечило отсутствие на кривой особых точек . Неформально это означает, что кривая везде красивая и гладкая и не содержит острых точек или выступов. В приведенных выше примерах константы и были выбраны как целые числа между и и и соответственно.Но в целом они могут принимать и другие значения. (Для использования в криптографии и должны поступать из специальных наборов чисел, называемых конечными полями ).
Вы можете узнать больше об эллиптических кривых в этой статье.
Добавление очков
Для эллиптической кривой мы можем определить сложение двух точек на ней, как в следующем примере.
Рассмотрим кривую
и две точки и, которые лежат на кривой.Теперь мы хотим найти ответ, для которого мы также хотели бы лечь на эллиптическую кривую. Если мы сложим их как векторы, мы получим — но, к сожалению, это не на кривой. Итак, мы определяем сложение с помощью следующих геометрических шагов.
Соединяем точки и прямой линией. Эта линия обычно пересекает кривую еще в одном месте. Затем мы отражаем точку на оси-оси.
Мы объявляем эту новую точку суммой и Итак
В нашем примере это означает, что
Другой пример:
(показано ниже), причем и у нас есть и.Следовательно,
Нам также нужно определение суммы, чтобы понять, что мы имеем в виду. В этом случае мы берем касательную к кривой в точке, а затем, как и раньше, находим пересечение этой касательной линии и кривой перед отражением точки. Это, вероятно, легче понять с помощью другого графика:
Здесь мы используем эллиптическую кривую
и рассмотрим точку. Мы нарисовали касательную к кривой, в которой она пересекает кривую во второй точке. Отражение по оси — дает Следовательно, мы говорим или
Теперь можно определить, что мы подразумеваем под любой точкой на кривой и любым натуральным числом
и так далее.
Единственная ситуация, в которой наше определение не работает, — это когда это отражение на -оси (что в случае, когда означает, что само лежит на -оси). В этом случае линия, которую мы используем для определения суммы, является вертикальной, и нет третьей точки, в которой она встречается с кривой.
Мы можем обойти эту проблему, добавив дополнительную точку к обычной плоскости, которая называется точкой на бесконечности и обозначается символом. Чтобы сложение работало для нашей исключительной ситуации, мы просто определяем Для любой точки, которую мы также определяем — так что с нашим новым В понятии сложения точка играет ту же роль, что и число в обычном сложении.
Оказывается, что для двух точек на эллиптической кривой нахождение такого числа (если оно существует) может потребовать огромных вычислительных мощностей, особенно когда оно велико. Криптография на основе эллиптических кривых использует этот факт: точки и могут использоваться как открытый ключ, а число как закрытый ключ. Кто угодно может зашифровать сообщение с помощью общедоступного открытого ключа (мы не будем вдаваться в подробности метода шифрования), но только человек (или компьютер), обладающий закрытым ключом, может их расшифровать.
АНБ и взлом данных
Криптография на основе эллиптических кривых имеет некоторые преимущества перед криптографией RSA, которая основана на сложности разложения больших чисел на множители, поскольку требуется меньше цифр для создания проблемы равной сложности. Следовательно, данные могут быть закодированы более эффективно (и, следовательно, быстрее), чем при использовании шифрования RSA. В настоящее время цифровая валюта Биткойн использует криптографию с эллиптической кривой, и вполне вероятно, что ее использование станет более распространенным по мере того, как все больше и больше данных оцифровываются.Однако стоит отметить, что пока еще никто не доказал, что взломать эллиптические кривые должно быть сложно — может быть новый подход, который может решить проблему в гораздо более короткие сроки. Действительно, в этой области работают многие математики и компьютерщики.
Государственные агентства цифрового шпионажа, такие как NSA и GCHQ, также очень заинтересованы в таких методах шифрования. Если бы существовал способ быстрого решения этой проблемы, то в одночасье были бы доступны большие объемы зашифрованных данных — и, например, обмен валюты Биткойн и больше не был бы безопасным.Также недавно выяснилось, что АНБ встроило «бэкдоры» в некоторые алгоритмы криптографии с эллиптическими кривыми, которые позволили им получить доступ к данным, которые отправители считали безопасными. Математика лежит в основе этой новой гонки цифровых вооружений.
Дополнительная литература
Чтобы узнать больше о разработке кодов, включая современную криптографию на основе эллиптических кривых, и их связях с математикой, хорошей отправной точкой является книга Уильяма Штейна « Элементарная теория чисел: простые числа, сравнения и секреты».Numberphile также осветило попытки АНБ обойти криптографию на основе эллиптических кривых в одном из своих неизменно превосходных видеороликов.
Об авторе
Эндрю Чемберс имеет степень магистра математики и преподает в Британской международной школе Пхукета, Таиланд.
 НОД и НОК.Арифметика остатковПрогрессииУравнения в целых числахСистема счисленияКомбинаторикаПериодичностьПринцип ДирихлеИндукцияГрафыГеометрияРебусыПрочее
НОД и НОК.Арифметика остатковПрогрессииУравнения в целых числахСистема счисленияКомбинаторикаПериодичностьПринцип ДирихлеИндукцияГрафыГеометрияРебусыПрочее Распределение ключей. Что это такое, как выполняется распределение ключей и как выбрать криптостойкий ключ
Распределение ключей. Что это такое, как выполняется распределение ключей и как выбрать криптостойкий ключ