Метод поиска в глубину лабиринт: Поиск в глубину на графе — Страница Михаила Медведева
НОУ ИНТУИТ | Лекция | Поиск на графе
Часто изучение свойств графа выполняется с помощью систематического просмотра каждой его вершины и каждого ребра. Определение некоторых простых свойств — например, вычисление степеней всех его вершин — выполняется просто перебором всех ребер (в любом порядке). Многие другие свойства графа связаны с путями на графах, поэтому они естественно определяются с помощью переходов от одной вершины к другой вдоль ребер графа. Эту базовую абстрактную модель используют почти все рассматриваемые нами алгоритмы обработки графов. В данной главе мы рассматриваем фундаментальные алгоритмы поиска на графах (graph search), которые используются для перемещения по графам с попутным изучением его структурных свойств.
Поиск на графе в таком виде эквивалентен исследованию лабиринта: коридоры лабиринта соответствуют ребрам графа, а места пересечения коридоров соответствуют вершинам графа. Когда программа меняет значение переменной с вершины v на вершину w из-за наличия ребра v-w, такое изменение можно рассматривать как переход в лабиринте из точки v в точку w. Мы начинаем данную главу с изучения систематического обхода лабиринтов. Это поможет нам наглядно представить, как базовые алгоритмы поиска на графах проходят через каждое ребро и каждую вершину графа.
В частности, рекурсивный алгоритм поиска в глубину в точности соответствует стратегии исследования лабиринта, описанной в разделе 18.1. Поиск в глубину представляет собой классический гибкий алгоритм, который применяется для решения задачи связности и множества других задач обработки графов. Возможны две реализации этого базового алгоритма: одна в виде рекурсивной процедуры и другая — с использованием явного стека. Замена стека очередью FIFO приводит к другому классическому алгоритму — поиску в ширину — который используется для решения других задач обработки графов, связанных с нахождением кратчайших путей.
Основной темой данной главы являются алгоритмы поиска в глубину, поиска в ширину, другие связанные с ними алгоритмы и их применение для обработки графов. Краткий обзор принципов поиска в глубину и поиска в ширину был приведен в
«Рекурсия и деревья»
, но здесь они будут рассмотрены как базовые принципы, в контексте классов обработки графов на основе поиска, и использованы для демонстрации взаимосвязи между различными алгоритмами обработки графов. В частности, мы рассмотрим общий принцип поиска на графах, который охватывает ряд классических алгоритмов обработки графов, в том числе и поиск в глубину и в ширину.
В качестве иллюстрации применения этих базовых методов поиска на графах для решения более сложных задач мы рассмотрим алгоритмы поиска связных компонентов, двусвязных компонентов, остовных деревьев и кратчайших путей, а также алгоритмы решения множества других задач обработки графов. Эти реализации наглядно продемонстрируют подход, который будет использован для решения более трудных задач в лекциях 19—22.
В конце главы мы рассмотрим основные вопросы, связанные с анализом алгоритмов на графах, в контексте практического сравнения нескольких различных алгоритмов определения количества связных компонентов в графе.
Исследование лабиринта
Поиск на графах иногда удобно рассматривать в терминах эквивалентной задачи, которая имеет долгую и интересную историю (см. раздел ссылок) — задачи поиска выхода из лабиринта, который состоит из перекрестков, соединенных коридорами. В этом разделе представлен подробный анализ базового метода исследования каждого коридора в любом заданном лабиринте. В некоторых лабиринтах достаточно одного простого правила, однако для большинства лабиринтов необходима более сложная стратегия (см.
рис.
18.1). Использование терминов лабиринт вместо граф, коридор вместо ребро и перекресток вместо вершина — просто семантическое различие, однако оно поможет глубже прочувствовать задачу.
Рис.
18.1.
Исследование лабиринта
Простой лабиринт можно полностью обойти, руководствуясь простым правилом » держитесь правой рукой за стену » . Это правило позволяет обойти весь лабиринт, который изображен в верхней части рисунка, пройдя по каждому коридору один раз в каждом направлении. Но если воспользоваться этим правилом для обхода лабиринта, содержащего цикл, мы вернемся в начальную точку, так и не побывав во всех местах лабиринта, как показано в нижней части рисунка.
Один из приемов исследования лабиринта без риска заблудиться известен еще с античных времен (как минимум, со времени легенды о Тесее и Минотавре) — он заключается в том, чтобы разматывать клубок по мере продвижения вглубь лабиринта. Нить клубка гарантирует, что мы всегда сможем выбраться из лабиринта, но, кроме этого, нам хотелось бы наверняка побывать в каждой части лабиринта и не проходить без необходимости по уже пройденному пути. Для этого нужно какое-то средство, позволяющее помечать те места, в которых мы уже были. В качестве такого средства годится и нить, однако мы воспользуемся другим методом, который больше похож на компьютерную реализацию.
Допустим, что на каждом перекрестке установлены лампы, которые сначала выключены, а в обоих концах каждого коридора имеются двери, которые в исходном состоянии закрыты. Допустим также, что в дверях имеются окна, лампы достаточно мощные, а коридоры достаточно прямые, так что, открыв дверь, можно увидеть, освещен или нет перекресток на другом конце коридора (даже если дверь на другом конце коридора закрыта). Наша цель заключается в том, чтобы зажечь все лампы и открыть все двери. Для достижения этой цели нужен набор правил, которым мы будем систематически следовать. Следующая стратегия исследования лабиринта, которую мы будем называть методом Тремо (Tremaux exploration), известна, по меньшей мере, с девятнадцатого столетия (см. раздел ссылок):
Наша цель заключается в том, чтобы зажечь все лампы и открыть все двери. Для достижения этой цели нужен набор правил, которым мы будем систематически следовать. Следующая стратегия исследования лабиринта, которую мы будем называть методом Тремо (Tremaux exploration), известна, по меньшей мере, с девятнадцатого столетия (см. раздел ссылок):
- Если на текущем перекрестке нет закрытых дверей, перейдите к шагу 3. Иначе откройте любую дверь любого коридора, ведущую из текущего перекрестка (и оставьте ее открытой).
- Если вы видите, что лампа, установленная на перекрестке на другом конце этого коридора уже включена, попробуйте открыть другую дверь на текущем перекрестке (шаг 1). Иначе (если перекресток на другом конце коридора не освещен), пройдите по коридору к этому перекрестку, разматывая при этом нить, включите свет и перейдите к шагу 1.
- Если все двери на текущем перекрестке открыты, проверьте, находитесь ли вы в отправной точке. Если да, то процесс окончен. Если нет, воспользуйтесь нитью, чтобы вернуться назад по коридору, который привел вас в этот перекресток в первый раз, сматывая нить по мере продвижения, и ищите другую закрытую дверь уже там (т.е. вернитесь к шагу 1).
На
рис.
18.2 и 18.3 представлен пример обхода графа и показано, что в данном случае, действительно, все лампы зажжены и все двери открыты. На них показан один из множества возможных успешных исходов исследования, ведь на каждом перекрестке можно открывать двери в любом порядке. Полезное упражнение — убедиться методом математической индукции, что этот метод эффективен всегда.
Лемма 18.1. При обходе лабиринта методом Тремо мы зажигаем все лампы и открываем все двери в лабиринте и завершаем обход там, где его начали.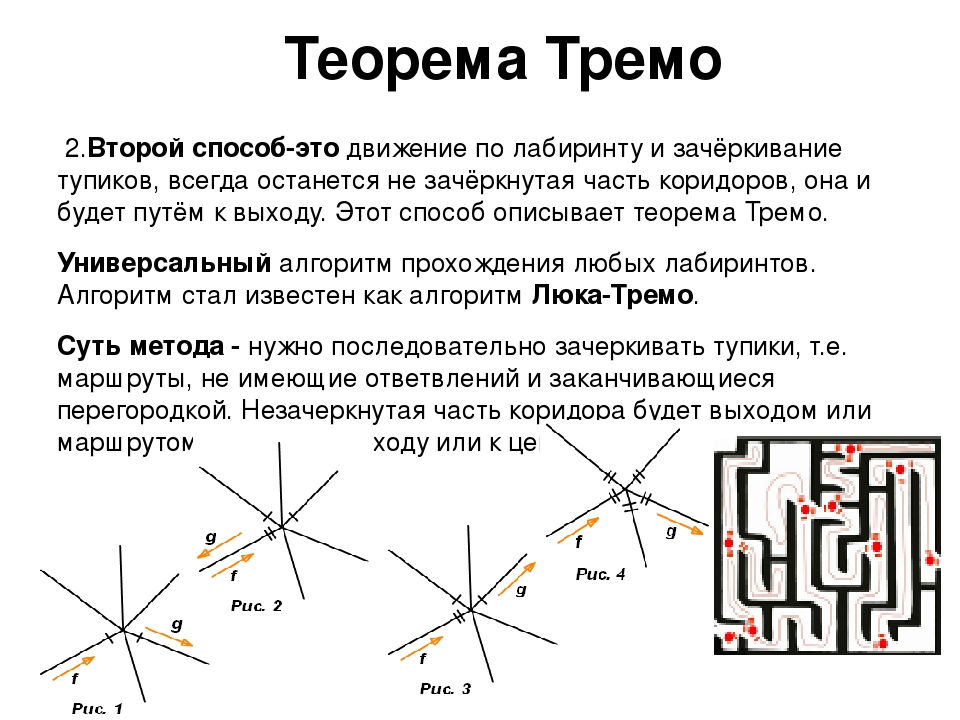
Доказательство. Докажем это утверждение по индукции. Вначале отметим, что оно выполняется в тривиальном случае, т.е. в лабиринте, который содержит один перекресток и ни одного коридора — мы просто включаем свет. Для любого лабиринта, который содержит более одного перекрестка, мы полагаем, что это свойство справедливо для всех лабиринтов с меньшим числом перекрестков. Достаточно показать, что мы посетили все перекрестки, поскольку мы открываем все двери на каждом посещенном перекрестке. Теперь рассмотрим первый коридор, выбранный на первом перекрестке, и разделим все перекрестки на два подмножества (
рис.
18.4): (1) те, которые мы можем достичь, выбрав этот коридор и не возвращаясь в исходную точку, и (2) те, которые мы не можем достичь, не вернувшись в исходную точку. По индуктивному предположению мы знаем, что посетили все перекрестки в (1) (игнорируя все коридоры, ведущие к исходному освещенному перекрестку) и вернулись на исходный перекресток. Тогда, применяя индуктивное предположение еще раз, мы знаем, что посетили все перекрестки (игнорируя коридоры, ведущие из отправной точки на перекрестки в (2), которые освещены).
Из подробного примера, представленного на
рис.
18.2 и
рис.
18.3, мы видим, что при выборе очередного коридора возможны четыре различные ситуации:
- Коридор не освещен, следовательно, мы выбираем его.
- Коридор уже был пройден (и в нем размотана нить), и мы возвращаемся по нему (сматывая нить).
- Дверь на другом конце коридора закрыта (но сам перекресток освещен), поэтому мы пропускаем этот коридор.
- Дверь на другом конце коридора открыта (и перекресток освещен), поэтому мы пропускаем этот коридор.

Первая и вторая ситуации описывают все коридоры, по которым мы проходим, сначала с одного его конца, а затем с другого. Третья и четвертая ситуация описывают все коридоры, которые мы пропускаем, сначала с одного его конца, а затем с другого.
Далее мы увидим, как этот способ исследования лабиринта преобразуется непосредственно в поиск на графе.
Рис.
18.2.
Пример применения метода Тремо для конкретного лабиринта
На этой диаграмме места, которые мы еще не посетили, заштрихованы (темные), а те места, в которых мы уже были, не заштрихованы (светлые). Мы полагаем, что на перекрестках горит свет, и что когда двери открыты с обоих концов коридора, этот коридор освещен. Исследование лабиринта мы начинаем с перекрестка 0 и выбираем коридор к перекрестку 2 (вверху слева). Далее мы продвигаемся по маршруту 6, 4, 3 и 5, по мере продвижения открывая двери в коридоры, зажигая свет на перекрестках и разматывая нить (слева). Открыв дверь, которая ведет из 5 в 0, мы видим, что перекресток 0 освещен, и поэтому игнорируем этот коридор (вверху справа). Аналогично, мы пропускаем коридор от 5 к 4 (справа, вторая диаграмма сверху), и нам остается только вернуться из 5 в 3 и далее в 4, сматывая нить в клубок. Когда мы откроем дверь коридора, ведущего из 4 в 5, мы видим через открытую дверь на другом конце коридора, что перекресток 5 освещен, и поэтому пропускаем этот коридор (справа внизу). Мы не прошли по коридору, соединяющему перекрестки 4 и 5, но мы осветили его, открыв двери с обоих концов.
Рис.
18.3.
Пример применения метода Тремо для конкретного лабиринта (продолжение)
Далее мы продвигаемся к перекрестку 7 (слева вверху), открываем дверь и видим, что перекресток 0 освещен (слева, вторая диаграмма сверху), после чего проходим к 1 (слева, третья диаграмма сверху). В этой точке большая часть лабиринта уже пройдена, и мы с помощью нити возвращаемся в начало пути, двигаясь от 1 до 7, далее до 4, до 6, до 2 и до 0. Вернувшись на перекресток 0, мы завершаем исследование, проверив коридоры, ведущие к перекрестку 5 (справа, вторая диаграмма снизу) и к перекрестку 7 (внизу справа), после чего все коридоры и перекрестки становятся освещенными. Здесь также коридоры, соединяющие перекрестки 0 с 5 и 0 с 7, освещены потому, что мы открыли двери с обоих концов, хотя и не проходили по ним.
В этой точке большая часть лабиринта уже пройдена, и мы с помощью нити возвращаемся в начало пути, двигаясь от 1 до 7, далее до 4, до 6, до 2 и до 0. Вернувшись на перекресток 0, мы завершаем исследование, проверив коридоры, ведущие к перекрестку 5 (справа, вторая диаграмма снизу) и к перекрестку 7 (внизу справа), после чего все коридоры и перекрестки становятся освещенными. Здесь также коридоры, соединяющие перекрестки 0 с 5 и 0 с 7, освещены потому, что мы открыли двери с обоих концов, хотя и не проходили по ним.
Рис.
18.4.
Разбиение лабиринта
Для доказательства методом индукции, что метод Тремо приводит во все точки лабиринта (вверху), мы разбиваем его на две части меньших размеров, удалив все ребра, соединяющие первый перекресток с любым другим перекрестком, который можно достичь из первого коридора, не возвращаясь через первый перекресток (внизу).
Упражнения
18.1. Предположим, что из лабиринта, показанного на
рис.
18.2 и
рис.
18.3, удалены перекрестки 6 и 7 (а также все ведущие к ним коридоры), зато добавлен коридор, который соединяет перекрестки 1 и 2. Покажите обход полученного лабиринта методом Тремо в стиле
рис.
18.2 и
рис.
18.3.
18.2. Какая из представленных ниже последовательностей не может быть последовательностью включения ламп при обходе методом Тремо лабиринта, представленного на
рис.
18.2 и 18.3?
0-7-4-5-3-1-6-2
0-2-6-4-3-7-1-5
intuit.ru/2010/edi»>0-5-3-4-7-1-6-2
0-7-4-6-2-1-3-5
18.3. Сколько существует различных путей обхода методом Тремо лабиринта, показанного на
рис.
18.2 и
рис.
18.3?
Метод поиска пути в лабиринте при наличии помех Текст научной статьи по специальности «Математика»
Метод поиска пути в лабиринте при наличии помех
Блинова Н.А. МГТУ им.Н.Э.Баумана [email protected] Филиппов М.В. МГТУ им.Н.Э.Баумана [email protected]
Аннотация
В работе проводится сравнительный анализ существующих методов решения задачи поиска оптимального пути в пространстве. Приводится описание методов, использующих поиск пути в графе. Предложен способ усовершенствования одного из существующих методов в случае, когда информация о расположении конечной точки неизвестна в начале пути.
1 Введение
Нахождения «пути из точки А в точку В» на первый взгляд не кажется такой сложной, поскольку каждый человек решает ее в повседневности чуть ли не каждый день, например, выбирая, как лучше добраться до работы. Однако, если передвигаться предстоит по неизвестной местности или в условиях, опасных для человеческой жизни, то задача существенно усложняется. В таком случае необходимо найти не просто путь, а кратчайший путь, причем не подвергая никого опасности в процессе исследования территории. Поэтому для решения подобной проблемы используется техника, а именно различные роботы.
В настоящее время для поиска пути в лабиринте существует множество методов, но все они работают в условиях, либо когда знания о расположения конечной точки не предполагаются, либо когда ее координаты известно изначально.
Целью настоящей статьи является метода поиска пути в лабиринте таким образом, чтобы путь прокладывался с учетом помех как физических, так и помех в каком-либо сигнале, передающем координаты конечной точки, которые изначально неизвестны.
2 Обзор существующих методов 2.1 Представление пространства
Существует два простых способа представления пространства: векторное и растровое.
В случае векторного представления используются навигационные графы. При таком подходе на местности или игровом уровне задаётся набор точек, которые затем соединяются в определенном порядке, образуя граф. Если две вершины графа соединены ребром, то между ними агент может беспрепятственно перемещаться. Каждая вершина в полученном графе представляет собой координаты точки в пространстве.
В случае растрового представления используются дискретное рабочее поле (или навигационная сетка) (ДРП). ДРП представляет собой ограниченную замкнутой линией фигуру, не обязательно прямоугольную, разбитую на ячейки, в частном случае — квадратные. Множество всех ячеек ДРП разбивается на подмножества:
— «проходимые» (свободные), т.е. при поиске пути их можно проходить;
— «непроходимые» (препятствия), путь через эту ячейку запрещён.
Соседние ячейки принято классифицировать двояко: в смысле окрестности Мура (Рис. 1)
Рис.1 Окрестность Мура и окрестности фон Неймана (Рис. 2).
Рис.2 Окрестность фон Неймана
Согласно теории графов дискретное рабочее поле есть ни что иное, как неориентированный планарный граф, то есть граф, который может быть изображен на плоскости без пересечения ребер, и в котором ребра можно проходить в любом направлении. Клетки рабочего поля являются вершинами графа. Из данной клетки в каждую соседнюю существует ребро, если эта клетка является проходимой.
Клетки рабочего поля являются вершинами графа. Из данной клетки в каждую соседнюю существует ребро, если эта клетка является проходимой.
При малом количестве простых препятствий меньше памяти используется при векторном представлении. При большом количестве препятствий, состоящих из множества ребер, меньше памяти используется при растровом представлении.
2.2 Методы поиска пути
Рассмотрим наиболее распространенные методы поиска пути.
Поиск в ширину (breadth-first search).
Один из основных алгоритмов на графах. Идея поиска в ширину состоит в том, чтобы посещать вершины в порядке их удаленности от некоторой заранее выбранной или указанной стартовой вершины а. Сам алгоритм можно понимать, как процесс «поджигания» графа: на нулевом шаге поджигаем только вершину. На каждом следующем шаге огонь с каждой уже горящей вершины перекидывается на всех её соседей; т.е. за одну итерацию алгоритма происходит расширение «кольца огня» в ширину на единицу (отсюда и название алгоритма).
В результате поиска в ширину находится путь кратчайшей длины в невзвешенном графе, т.е. путь, содержащий наименьшее число рёбер. Однако, метод перестает работать во взвешенных средах.
Поиск в глубину (depth-first search). Вероятно, наиболее важная ввиду многочисленности приложений стратегия обхода графа. Идея этого метода — идти вперед в неисследованную область, пока это возможно, если же вокруг все исследовано, отступить на шаг назад и искать новые возможности для продвижения вперед.
Алгоритм позволяет построить обход ориентированного или неориентированного не-взвешенного графа, при котором посещаются все вершины, доступные из начальной вершины.![]() Также, как и предыдущий, метод перестает работать во взвешенных средах.
Также, как и предыдущий, метод перестает работать во взвешенных средах.
Волновой метод (метод Ли). Метод поиска пути на планарном графе (дискретном рабо-
чем поле) используется наиболее часто. Принадлежит к алгоритмам, основанным на методах поиска в ширину и предназначен для нахождения кратчайшего пути от стартовой ячейки к конечной ячейке, если это возможно, либо, при отсутствии пути, выдать сообщение о непроходимости.
Работа алгоритма включает в себя три этапа: инициализацию, распространение волны и восстановление пути.
Во время инициализации строится образ множества ячеек обрабатываемого поля, каждой ячейке приписываются атрибуты проходимости или непроходимости, запоминаются стартовая и финишная ячейки.
Далее, от стартовой ячейки порождается шаг в соседнюю ячейку, при этом проверяется, проходима ли она, и не принадлежит ли ранее меченной в пути ячейке.
При выполнении условий проходимости и непринадлежности её к ранее помеченным в пути ячейкам, в атрибут ячейки записывается число, равное количеству шагов от стартовой ячейки (от стартовой ячейки на первом шаге это будет 1). Каждая ячейка, меченая числом шагов от стартовой ячейки становится стартовой и из неё порождаются очередные шаги в соседние ячейки. При таком переборе будет найден путь от начальной ячейки к конечной, либо очередной шаг из любой порождённой в пути ячейки будет невозможен.
Восстановление кратчайшего пути происходит в обратном направлении: при выборе ячейки от финишной ячейки к стартовой на каждом шаге выбирается ячейка, имеющая атрибут расстояния от стартовой на единицу меньше текущей ячейки.
Данный метод всегда обеспечивает нахождение кратчайшего путь и отличается работоспособностью во взвешенных средах. Недостатком его является большое потребление памяти.
Недостатком его является большое потребление памяти.
Метод поиска А* («A-star»). Относится к эвристическим методам поиска. Используется для поиска кратчайшего пути между двумя вершинами графа с положительными весами ребер.
Он просматривает сначала те маршруты через вершины, которые «кажутся» ведущими к цели. От жадного алгоритма его отличает то, что при выборе вершины он учитывает, помимо прочего, весь пройденный до неё путь. Чтобы распознать такие вершины, каждой известной вершине сопоставляется значение, равное длине кратчайшего пути от начальной
вершины до конечной, который пролегает через выбранную вершину. Вершины с наименьшим значением избираются в первую очередь.
Функция для вершины определяется так: /(.х) = g(x)-h(x) (1)
где
g(x) — функция, значение которой равно стоимости пути от начальной вершины до текущей,
X) — эвристическая функция, оценивающая стоимость пути от текущей вершины до конечной.
Метод делит вершины на три класса:
1) неизвестные вершины: эти вершины еще не были найдены. Путь к ним еще неизвестен. В начале работы алгоритма все вершины, кроме начальной, принадлежат к классу неизвестных.
2) известные вершины (OpenList): содержат уже известный (возможно, не оптимальный) путь к этим вершинам. Все известные вершины вместе со значениями сохраняются в списке. Из этого списка выбираются, в первую очередь, перспективные вершины. В начале работы алгоритма к известным вершинам принадлежит только начальная вершина.
3) полностью исследованные вершины (ClosedList): до этих вершин уже известен кратчайший путь. Полностью исследованные вершины добавляются к так называемому закрытому списку, чтобы предотвратить многократное исследование уже исследованных вершин. Список полностью исследованных вершин в начале работы алгоритма пустой.
Полностью исследованные вершины добавляются к так называемому закрытому списку, чтобы предотвратить многократное исследование уже исследованных вершин. Список полностью исследованных вершин в начале работы алгоритма пустой.
Алгоритм останавливается, когда конечная вершина попадает в список полностью исследованных вершин. Найденный путь воспроизводится с помощью указателей на предыдущую вершину. Если список известных вершин пустеет, то решения задачи не существует и алгоритм прекращает поиск.
Данный алгоритм всегда находит кратчайший путь и отличается работоспособностью во взвешенных средах. Однако, как и волновой метод, он требует больших затрат памяти.
3 Описание разработанного метода
На основе изложенных выше результатов сравнительного анализа для разработки метода решения задачи поиска пути при наличии помех в качестве базового был использован волновой алгоритм поиска. В данной работе представлено дальнейшее развитие этого алго-
ритма для случая, когда координаты цели заранее неизвестны, но в дальнейшем информация о них может появиться. Кроме того предложен способ уменьшения затрат памяти для хранения карты ДРП.
Можно выделить следующие этапы работы метода:
1. Чтобы обойти лабиринт без повторного посещения изученных позиций, необходимо сформировать открытый и закрытый списки. В открытом списке будут содержаться позиции, подлежащие исследованию. В закрытом списке будут содержаться уже исследованные позиции.
2. Для того чтобы выбрать следующую позицию для исследования наилучшим образом, необходимо использовать некоторые приоритетные значения. п) — проходимость текущей позиции, (эта функция отвечает за преодоление физических помех).
п) — проходимость текущей позиции, (эта функция отвечает за преодоление физических помех).
Для вычисления расстояния от текущей позиции до конечной используется стандартная метрика Евклида:
fin) = J(xf — хп)2 + (У/ — Уп)2,
(3)
где (xn,yn) — координаты текущей позиции, (х/,у/) — координаты конечной точки.
Весовая функция, способная учитывать как расстояние от начальной позиции до текущей, так и возможность расчета расстояния от текущей позиции до конечной рассчитывается по следующей формуле:
дп) = fls(n)’ если fla9 = false’> (4)
[ls(ri) + lf(n), если flag = true где параметр flag — флаг получения информации о координатах расположения целевой точки.
В волновом методе и методе поиска А* для хранения карты местности используются массивы, что приводит к большим затратам памяти. В данной работе хранение карты реализуется при помощи квадродеревьев, что уменьшает необходимое количество памяти, необходимое для хранения, но потребует более сложных алгоритмов в связи с разными размерами ячеек. Пример хранения растровой карты представлен на Рис. 3
Рис.3 Хранение растровой карты с помощью квадродерева
Использование квадродерева позволяет также сократить и время расчета по сравнению с базовым методом, что будет показано ниже в разделе, описывающем результаты численных расчетов.
4 Результаты численных расчетов
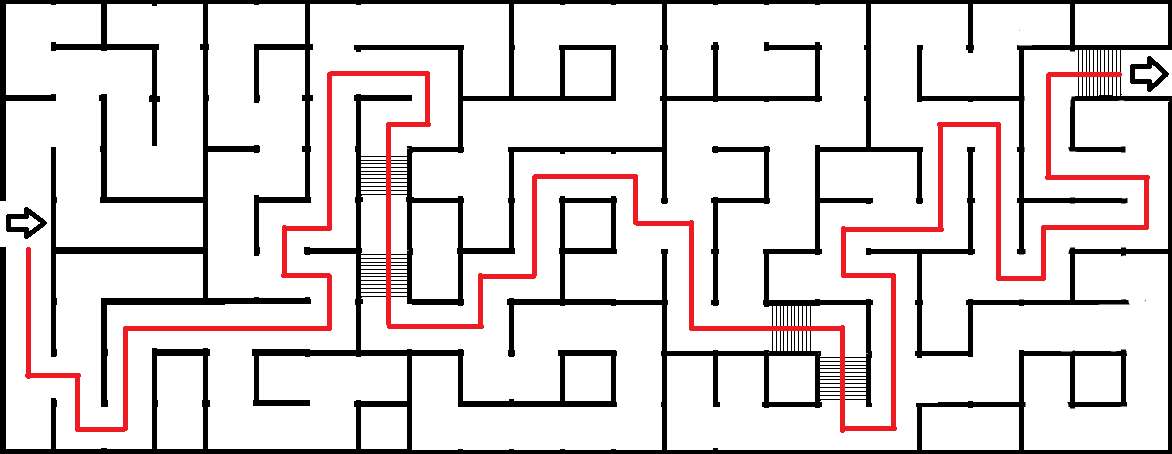
На основе описанного выше метода был разработан программный комплекс построения пути в лабиринте при наличии помех. Пример построения пути представлен на Рис.4.
Пример построения пути представлен на Рис.4.
Рис. 4 Карта лабиринта с проложенным путем
На Рис.4 голубые клетки — свободные, серые — занятые преградой, коричневые — представляют помеху, зеленые — начальная и конечная точка пути, желтые — проложенный путь. Помеха имеет отличную от свободной клетки проходимость, а также она может поглотить сигнал, передающий информацию о целевой точке.
В данном разделе приводятся также результаты исследование скорости работы программного комплекса и количества исследованных точек. Проведено сравнение с оригинальным волновым методом.
Для оценки указанных параметров для каждого размера карты от 10х10 клеток до 35х35 клеток было сгенерировано 50 лабиринтов с характеристиками:
1. Вероятность появления преграды — 10%
2. Вероятность появления помехи — 10%
3. Путь прокладывался из точки, находящейся в среднем ряду в крайнем левом столбце, в точку, находящейся в правом верхнем углу карты
4. Дальность распространения сигнала -15
На Рис.5 представлена зависимость количества обойденных точек, потребовавшегося при поиске пути, в зависимости от размера карты.
900
-Модификация
i 800
О
10 15 20 25 30
Размер карты
Рис. 200 Q.
200 Q.
1
% 150 т Q. CD
100 50 0
Рис.6 Зависимость времени определения пути от размера карты.
Как видно из графика, время работы представленного метода по сравнению с исходным методом меньше при любом размере карты даже при фиксированной дальности сигнала. Увеличение быстродействия связано с использованием алгоритма квазидеревьев, который также позволил существенно сократить затраты объема памяти.
Заключение
В работе представлен метод определения пути в лабиринте с учетом помех, которые могут препятствовать движению объекта и распространению сигнала. Проведенные численные расчеты показали, что данный метод уменьшает количество обойденных точек и обладает большим быстродействием по сравнению с обычно используемыми.
Список литературы
Применение графов в различных областях жизни людей. [Электронный ресурс] — Режим до-ступа:ht:tp://obuchonok.ru/node/1321 (Дата обращения: 24.12.2018)
Клеточные автоматы [Электронный ресурс] — Режим доступа: Мр://осо.ога.щ/клеточные автоматы/ (Дата обращения: 24.12.2018)
Lee, C.Y., «An Algorithm for Path Connections and Its Applications», IRE Transactions on Electronic Computers, vol. EC-10, number 2, pp. 364—365..
Алгоритмы поиска пути [Электронный ресурс] — Режим доступа: http://pmg.org.ru/ai/stout.htm (дата обращения: 21.05.2018)
Stefan Edelkamp, Stefan Schrödl. Heuristic search: theory and applications. / Morgan Kaufmann Publishers, 2012. 712 с.,
Heuristic search: theory and applications. / Morgan Kaufmann Publishers, 2012. 712 с.,
Использование квадродеревьев при расчёте пробок 2ГИС. [Электронный ресурс] — Режим до-ступа:ht:tps://habrcom/company/2gis/blog/205742/ (Дата обращения: 24.12.2018)
Introduction to A [Электронный ресурс] — Режим до-ступа:ht:tps://www.redblobgames.com/pathfinding/ a-star/introduction.html (дата обращения: 23.05.2018)
Информированный поиск и исследование пространства состояний [Электронный ресурс]- Режим доступа : http://iskhacov.narod.ru/biblio-/InfPoiskStuart.pdf (дата обращения: 21.05.2018)
10 15 20 25 30 35
Размер карты
Алгоритм создания лабиринта — Maze generation algorithm
Автоматизированные методы создания лабиринтов
Поколения Maze алгоритмы автоматизированы методы для создания лабиринтов .
Методы, основанные на теории графов
Анимация метода на основе теории графов (рандомизированный поиск в глубину)
Лабиринт можно создать, начав с заранее заданного расположения ячеек (чаще всего прямоугольной сетки, но возможны и другие варианты) с участками стен между ними. Это заданное расположение можно рассматривать как связанный граф, края которого представляют возможные участки стен, а узлы — ячейки. Затем можно считать, что целью алгоритма создания лабиринта является создание подграфа, в котором сложно найти маршрут между двумя конкретными узлами.
Если подграф не связан , то есть области графа, которые теряются, потому что они не вносят вклад в пространство поиска. Если в графе есть петли, то между выбранными узлами может быть несколько путей. По этой причине создание лабиринта часто рассматривается как создание случайного связующего дерева . Циклы, которые могут сбивать с толку наивные решатели лабиринта, могут быть введены путем добавления случайных ребер к результату в ходе работы алгоритма.
Циклы, которые могут сбивать с толку наивные решатели лабиринта, могут быть введены путем добавления случайных ребер к результату в ходе работы алгоритма.
Анимация показывает этапы создания лабиринта для графика, который не находится на прямоугольной сетке. Сначала компьютер создает случайный планарный граф G, показанный синим цветом, и его двойственный F, показанный желтым. Во-вторых, компьютер проходит F, используя выбранный алгоритм, такой как поиск в глубину, окрашивая путь в красный цвет. Во время обхода, когда красный край пересекает синий край, синий край удаляется. Наконец, когда все вершины F были посещены, F стирается и два ребра из G, одно для входа и одно для выхода, удаляются.
Рандомизированный поиск в глубину
Анимация генератора с использованием поиска в глубину
Этот алгоритм, также известный как алгоритм «рекурсивного отслеживания с возвратом», представляет собой рандомизированную версию алгоритма поиска в глубину .
Этот подход, который часто реализуется с помощью стека, является одним из простейших способов создания лабиринта с помощью компьютера. Представьте, что пространство для лабиринта представляет собой большую сетку ячеек (например, большую шахматную доску), каждая ячейка начинается с четырех стен. Начиная со случайной ячейки, компьютер затем выбирает случайную соседнюю ячейку, которая еще не была посещена. Компьютер удаляет стену между двумя ячейками, отмечает новую ячейку как посещенную и добавляет ее в стек, чтобы облегчить возврат. Компьютер продолжает этот процесс, при этом ячейка, у которой нет невидимых соседей, считается тупиком. Находясь в тупике, он возвращается по пути, пока не достигает ячейки с непосещенным соседом, продолжая генерацию пути, посещая эту новую, непосещенную ячейку (создавая новое соединение). Этот процесс продолжается до тех пор, пока не будет посещена каждая ячейка, в результате чего компьютер полностью откатится к начальной ячейке. Мы можем быть уверены, что каждую камеру посетят.
Как указано выше, этот алгоритм включает глубокую рекурсию, которая может вызвать проблемы с переполнением стека на некоторых компьютерных архитектурах. Алгоритм можно преобразовать в цикл, сохранив информацию об обратном отслеживании в самом лабиринте. Это также обеспечивает быстрый способ отображения решения, начав с любой заданной точки и вернувшись к началу.
Смещение горизонтального прохода
Лабиринты, созданные с помощью поиска в глубину, имеют низкий коэффициент ветвления и содержат много длинных коридоров, потому что алгоритм исследует как можно дальше вдоль каждой ветви перед отслеживанием с возвратом.
Рекурсивная реализация
Рандомизированный поиск в глубину на гексагональной сетке
Поиск в глубину алгоритм генерации лабиринта часто реализуются с использованием обратной отслеживани . Это можно описать следующей рекурсивной программой:
- Учитывая текущую ячейку в качестве параметра,
- Отметить текущую ячейку как посещенную
- Пока в текущей ячейке есть непосещенные соседние ячейки
- Выберите одного из непосещаемых соседей
- Убрать стену между текущей ячейкой и выбранной ячейкой
- Рекурсивно вызывать процедуру для выбранной ячейки
который вызывается один раз для любой начальной ячейки в области.
Итеративная реализация
Недостатком первого подхода является большая глубина рекурсии — в худшем случае может потребоваться повторение процедуры для каждой ячейки обрабатываемой области, что может превышать максимальную глубину стека рекурсии во многих средах. В качестве решения тот же метод поиска с возвратом может быть реализован с явным стеком , которому обычно позволяют расти намного без вреда.
- Выберите начальную ячейку, отметьте ее как посещенную и поместите в стек
- Пока стек не пуст
- Извлечь ячейку из стека и сделать ее текущей ячейкой
- Если у текущей ячейки есть соседи, которые не были посещены
- Поместить текущую ячейку в стек
- Выберите одного из непосещаемых соседей
- Убрать стену между текущей ячейкой и выбранной ячейкой
- Отметьте выбранную ячейку как посещенную и поместите ее в стек
Рандомизированный алгоритм Краскала
Анимация создания лабиринта 30 на 20 с использованием алгоритма Крускала.
Этот алгоритм представляет собой рандомизированную версию алгоритма Крускала .
- Создайте список всех стен и создайте набор для каждой ячейки, каждая из которых содержит только эту ячейку.
- Для каждой стены в произвольном порядке:
- Если клетки, разделенные этой стеной, принадлежат разным наборам:
- Удалить текущую стену.
- Присоединяйтесь к наборам ранее разделенных ячеек.
- Если клетки, разделенные этой стеной, принадлежат разным наборам:
Есть несколько структур данных, которые можно использовать для моделирования наборов ячеек. Эффективная реализация, использующая структуру данных с непересекающимися наборами, может выполнять каждое объединение и операцию поиска на двух наборах за почти постоянное амортизированное время (в частности, время; для любого правдоподобного значения ), поэтому время работы этого алгоритма по существу пропорционально числу стен, доступных для лабиринта.
О ( α ( V ) ) {\ Displaystyle О (\ альфа (V))} α ( Икс ) < 5 {\ Displaystyle \ альфа (х) <5} Икс {\ displaystyle x}
Неважно, является ли список стен изначально рандомизированным или стена выбирается случайным образом из неслучайного списка, любой способ так же легко кодировать.
Поскольку эффект этого алгоритма заключается в создании минимального остовного дерева из графа с равновзвешенными ребрами, он имеет тенденцию создавать регулярные шаблоны, которые довольно легко решить.
Рандомизированный алгоритм Прима
Анимация создания лабиринта 30 на 20 с использованием алгоритма Прима.
Этот алгоритм представляет собой рандомизированную версию алгоритма Прима .
- Начните с сетки, полной стен.
- Выберите ячейку, отметьте ее как часть лабиринта. Добавьте стены камеры в список стен.
- Пока в списке есть стены:
- Выберите случайную стену из списка. Если посещена только одна из двух ячеек, которые разделяет стена, то:
- Сделайте стену проходом и отметьте непосещаемую ячейку как часть лабиринта.

- Добавьте соседние стены ячейки в список стен.
- Сделайте стену проходом и отметьте непосещаемую ячейку как часть лабиринта.
- Удалите стену из списка.
- Выберите случайную стену из списка. Если посещена только одна из двух ячеек, которые разделяет стена, то:
Обратите внимание, что простой запуск классических Prim на графе со случайными весами ребер приведет к созданию лабиринтов, стилистически идентичных лабиринту Kruskal, потому что они оба являются алгоритмами минимального остовного дерева. Вместо этого этот алгоритм вводит стилистические вариации, поскольку края, расположенные ближе к начальной точке, имеют меньший эффективный вес.
Модифицированная версия
Хотя классический алгоритм Прима хранит список ребер, для создания лабиринта мы могли бы вместо этого поддерживать список смежных ячеек. Если случайно выбранная ячейка имеет несколько ребер, которые соединяют ее с существующим лабиринтом, выберите одно из этих ребер случайным образом. Это будет иметь тенденцию к разветвлению немного больше, чем версия на основе ребер выше.
Упрощенная версия
Алгоритм можно еще больше упростить путем случайного выбора ячеек, которые соседствуют с уже посещенными ячейками, вместо отслеживания весов всех ячеек или ребер.
Обычно найти путь к начальной ячейке относительно легко, но трудно найти путь где-либо еще.
Алгоритм Вильсона
Все вышеперечисленные алгоритмы имеют различного рода предубеждения: поиск в глубину смещен в сторону длинных коридоров, в то время как алгоритмы Крускала / Прима смещены во многие короткие тупики. Алгоритм Уилсона, с другой стороны, генерирует несмещенную выборку из равномерного распределения по всем лабиринтам, используя случайные блуждания со стиранием цикла .
Мы начинаем алгоритм с инициализации лабиринта одной произвольно выбранной ячейкой. Затем мы начинаем с новой произвольно выбранной ячейки и выполняем случайное блуждание до тех пор, пока не дойдем до ячейки, уже находящейся в лабиринте — однако, если в какой-то момент случайное блуждание достигает своего собственного пути, образуя цикл, мы стираем цикл с пути прежде чем продолжить.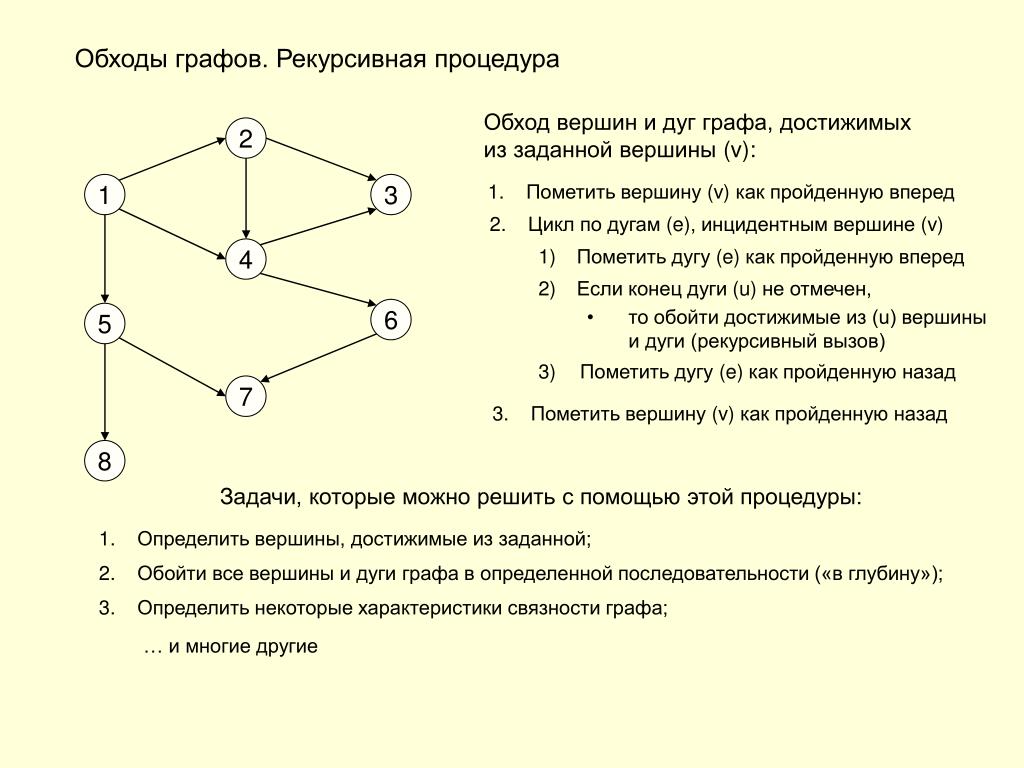 Когда путь доходит до лабиринта, мы добавляем его в лабиринт. Затем мы выполняем еще одно случайное блуждание с удалением цикла из другой произвольной начальной ячейки, повторяя, пока все ячейки не будут заполнены.
Когда путь доходит до лабиринта, мы добавляем его в лабиринт. Затем мы выполняем еще одно случайное блуждание с удалением цикла из другой произвольной начальной ячейки, повторяя, пока все ячейки не будут заполнены.
Эта процедура остается беспристрастной независимо от того, какой метод мы используем для произвольного выбора начальных ячеек. Таким образом, для простоты мы всегда можем выбрать первую незаполненную ячейку, например, слева направо, сверху вниз.
Алдос-Бродер алгоритм
Алгоритм Олдоса-Бродера также создает однородные остовные деревья.
- Выберите случайную ячейку в качестве текущей и отметьте ее как посещенную.
- Пока есть непосещенные клетки:
- Выберите случайного соседа.
- Если к выбранному соседу никто не заходил:
- Уберите стену между текущей ячейкой и выбранным соседом.
- Отметьте выбранного соседа как посещенного.
- Сделать выбранного соседа текущей ячейкой.
Рекурсивный метод деления
Лабиринты можно создавать с помощью рекурсивного деления , алгоритм которого работает следующим образом: Начните с пространства лабиринта без стен. Назовите это камерой. Разделите камеру произвольно расположенной стеной (или несколькими стенами), где каждая стена содержит произвольно расположенный проход внутри нее. Затем рекурсивно повторите процесс для подкамер, пока все камеры не станут минимального размера. Этот метод приводит к созданию лабиринтов с длинными прямыми стенами, пересекающими их пространство, что упрощает определение областей, которых следует избегать.
Рекурсивное создание лабиринта
Например, в прямоугольном лабиринте постройте в случайных точках две стены, перпендикулярные друг другу. Эти две стены делят большую камеру на четыре меньшие камеры, разделенные четырьмя стенками. Выберите три из четырех стен наугад и откройте отверстие размером в одну ячейку в случайном месте в каждой из трех. Продолжайте таким же образом рекурсивно, пока каждая камера не станет шириной в одну ячейку в любом из двух направлений.
Продолжайте таким же образом рекурсивно, пока каждая камера не станет шириной в одну ячейку в любом из двух направлений.
Простые алгоритмы
3D-версия алгоритма Прима. Вертикальные слои пронумерованы от 1 до 4 снизу вверх. Лестница наверх обозначена «/»; лестница вниз с «\» и лестница вверх и вниз с «x». Исходный код включен в описание изображения.
Существуют и другие алгоритмы, которым требуется достаточно памяти только для хранения одной линии двухмерного лабиринта или одной плоскости трехмерного лабиринта. Алгоритм Эллера предотвращает петли, запоминая, какие ячейки в текущей строке соединены через ячейки в предыдущих строках, и никогда не удаляет стены между любыми двумя уже соединенными ячейками. Алгоритм Sidewinder начинается с открытого прохода вдоль всего верхнего ряда, а последующие ряды состоят из более коротких горизонтальных проходов с одним соединением с проходом выше. Алгоритм Sidewinder тривиально решать снизу вверх, потому что он не имеет восходящих тупиков. Учитывая начальную ширину, оба алгоритма создают идеальные лабиринты неограниченной высоты.
Большинство алгоритмов создания лабиринта требуют поддержания отношений между ячейками внутри него, чтобы гарантировать, что конечный результат будет решаемым. Однако допустимые односвязные лабиринты могут быть созданы, если сосредоточиться на каждой ячейке независимо. Лабиринт двоичного дерева — это стандартный ортогональный лабиринт, в котором каждая ячейка всегда имеет проход, ведущий вверх или ведущий влево, но не оба одновременно. Чтобы создать лабиринт двоичного дерева, для каждой ячейки подбросьте монетку, чтобы решить, добавлять ли проход, ведущий вверх или влево. Всегда выбирайте одно и то же направление для ячеек на границе, и конечным результатом будет допустимый односвязный лабиринт, который выглядит как двоичное дерево , с верхним левым углом его корнем. Как и в случае с Сайдвиндером, лабиринт двоичного дерева не имеет тупиков в направлении смещения.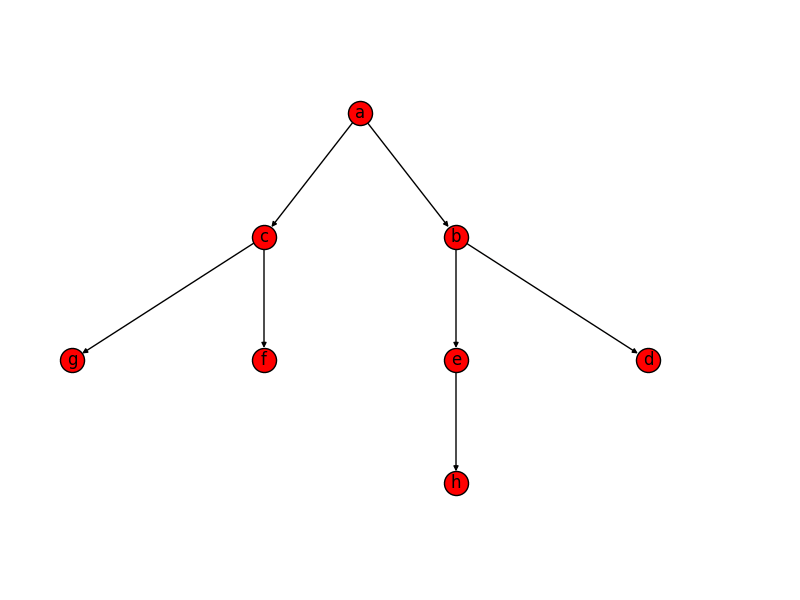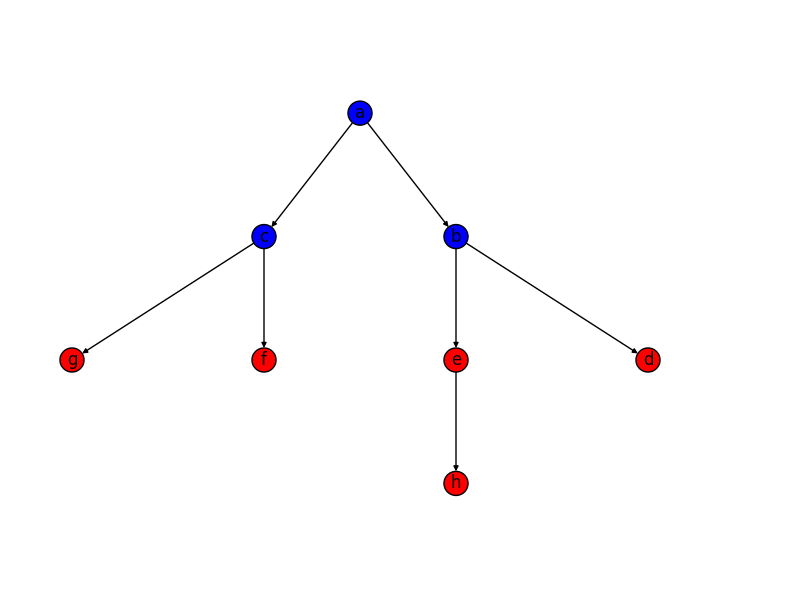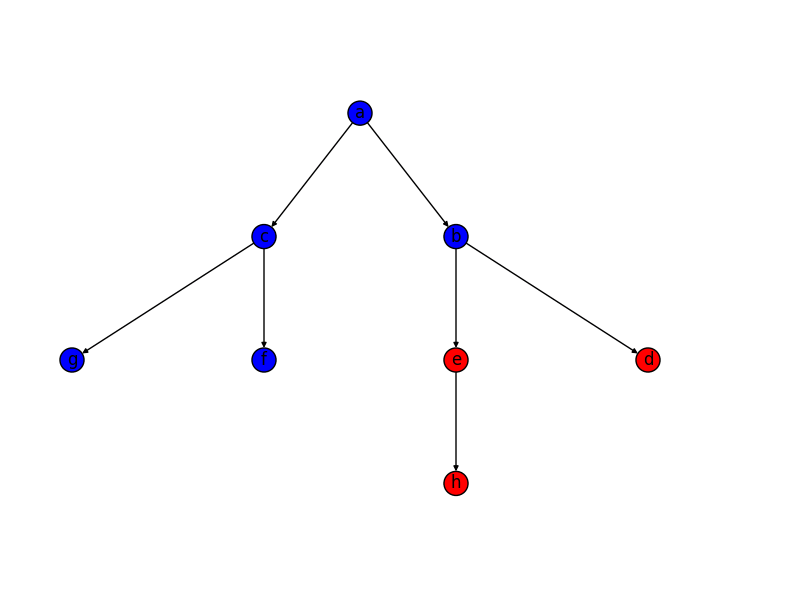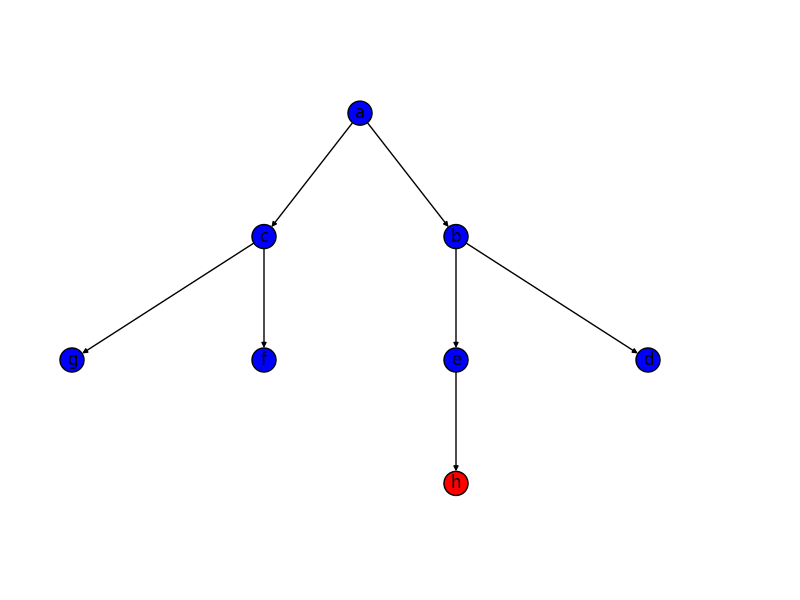
Связанная форма подбрасывания монеты для каждой ячейки — создание изображения с использованием случайного сочетания символов прямой и обратной косой черты. Это не создает действительный односвязный лабиринт, а скорее набор замкнутых петель и уникурсальных проходов. (В руководстве для Commodore 64 представлена программа BASIC, использующая этот алгоритм, но с использованием вместо этого графических символов диагональной линии PETSCII для более плавного графического отображения .)
Алгоритмы сотовых автоматов
Некоторые типы клеточных автоматов могут быть использованы для создания лабиринтов. Два хорошо известных таких клеточных автомата, Maze и Mazectric, имеют цепочки правил B3 / S12345 и B3 / S1234. В первом случае это означает, что клетки выживают из поколения в поколение, если у них есть от одного до пяти соседей . В последнем случае это означает, что клетки выживают, если у них есть от одного до четырех соседей. Если у клетки ровно три соседа, она рождается. Это похоже на «Игру жизни» Конвея в том, что модели, в которых одна живая клетка не соседствует с 1, 4 или 5 другими живыми клетками в любом поколении, будут вести себя идентично с ней. Однако для больших шаблонов он ведет себя совсем не так, как Life.
При случайном стартовом образце эти генерирующие лабиринты клеточные автоматы будут развиваться в сложные лабиринты с четко очерченными стенами, очерчивающими коридоры. Mazecetric с правилом B3 / S1234 имеет тенденцию создавать более длинные и прямые коридоры по сравнению с Maze с правилом B3 / S12345. Поскольку эти правила клеточного автомата детерминированы , каждый сгенерированный лабиринт однозначно определяется своим случайным начальным шаблоном. Это серьезный недостаток, поскольку лабиринты обычно относительно предсказуемы.
Подобно некоторым методам, основанным на теории графов, описанным выше, эти клеточные автоматы обычно генерируют лабиринты из одного начального шаблона; следовательно, обычно будет относительно легко найти путь к начальной ячейке, но труднее найти путь в другом месте.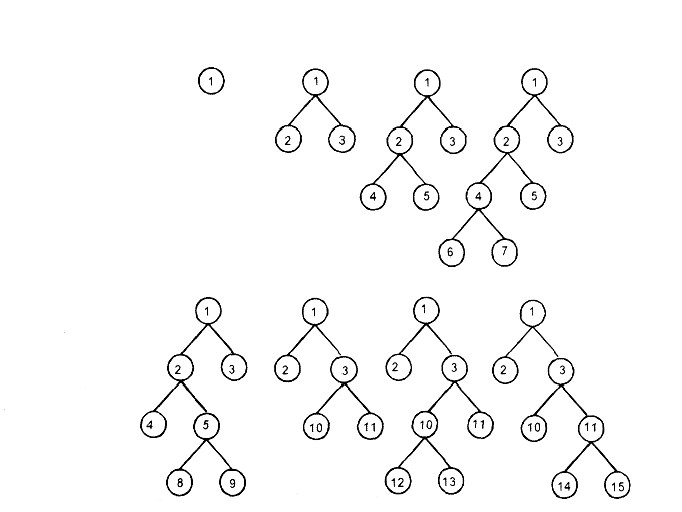
Смотрите также
Рекомендации
внешняя ссылка
Выбор оптимального алгоритма поиска в Python | by Дмитрий ПереводIT | NOP::Nuances of Programming
Когда дело касается обучения, мы, как правило, используем один из двух основных подходов: идём либо вширь и стараемся охватить как можно больший спектр области, либо вглубь и пытаемся получить конкретику в изучаемой нами теме. Преуспевающие в этом люди отмечают, что всё изучаемое нами в жизни, начиная от алгоритмов и заканчивая жизненными навыками, в определённой степени подразумевает совмещение этих подходов.
Здесь мы познакомимся с двумя основными алгоритмами поиска, а именно “поиском в глубину” (DFS) и “поиском в ширину” (BFS), которые лягут в основу понимания более сложных алгоритмов.
Содержание:
- Обход дерева.
- Поиск в глубину.
- Поиск в ширину.
- Сравнение предлагаемых алгоритмов.
Давайте начнём с обхода дерева.
Поскольку деревья — это разновидность графа, их обход, иначе называемый поиск по дереву, является видом обхода графа. Тем не менее для дерева этот процесс отличается меньшей масштабностью.
Обход дерева обычно известен как проверка (посещение) или обновление каждого узла по одному разу без повторений. Поскольку все узлы связаны рёбрами, начинаем мы всегда с корневого. Это означает, что нельзя произвольно обратиться к любому узлу дерева.
К выполнению обхода существует три подхода:
- прямой;
- симметричный;
- обратный.
Прямой обход
В этом способе мы сначала считываем данные с корневого узла, затем перемещаемся к левому поддереву, а потом к правому. В связи с этим посещаемые нами узлы (а также вывод их данных) следуют тому же шаблону, в котором сначала мы выводим данные корневого узла, затем данные его левого поддерева, а затем правого.
Алгоритм:
Пока все узлы не будут посещены
Шаг 1 − Посещение корневого узла
Шаг 2 − Рекурсивный обход левого поддерева
Шаг 3 − Рекурсивный обход правого поддерева
Прямой обход
Мы начинаем с корневого узла и, следуя прямому порядку обхода, сначала посещаем сам этот узел, а затем переходим к его левому поддереву, которое обходим по тому же принципу. Это продолжается, пока все узлы не будут посещены. В итоге порядок вывода будет таким:
Это продолжается, пока все узлы не будут посещены. В итоге порядок вывода будет таким: 1,2,3,4,5,6,7.
Симметричный обход
При симметричном обходе мы проходим по пути к самому левому потомку, затем возвращаемся к корню, посещаем его и следуем к правому потомку.
Алгоритм:
Пока все узлы не будут посещены
Шаг 1 − Рекурсивный обход левого поддерева
Шаг 2 − Посещение корневого узла
Шаг 3 − Рекурсивный обход правого поддерева
Симметричный обход
Начав от корневого узла 4, мы рекурсивно перебираем его левое поддерево, используя такой же симметричный порядок, затем посещаем сам корневой узел и далее перебираем правое поддерево.
Обратный обход
При обратном подходе мы сначала посещаем левого потомка, затем правого и по завершении обхода поддеревьев считываем корень.
Алгоритм:
Пока все узлы не будут посещены
Шаг 1 − Рекурсивный обход левого поддерева
Шаг 2 − Рекурсивный обход правого поддерева
Шаг 3 − Посещение корневого узла
Обратный обход
Становится ясно, что алгоритмы классифицируются на основе последовательности посещения узлов.
Здесь я снова упомяну, что есть две основных техники, которые мы можем использовать для обхода и посещения каждого узла исключительно по одному разу: поиск в глубину или поиск в ширину.
В этом способе мы всегда посещаем самый углублённый узел, затем идём назад и следуем другим путём, достигая другого конечного узла.
Обратите внимание, что в этом алгоритме для запоминания маршрута к конечному узлу и обратно используется механизм стека.
При таком подходе нам нужно обойти всю ветку дерева и все прилегающие узлы. Поэтому для отслеживания текущего узла требуется подход “последним вошёл — первым вышел”, который реализуется через стек. После достижения самого глубокого узла все остальные узлы извлекаются из стека. Затем происходит обход прилегающих узлов, которые ещё не посещались.
Если бы вместо стека использовалась очередь, представляющая подход “первым вошел — первым вышел”, то мы бы не смогли идти в глубину, не удаляя из очереди текущий узел.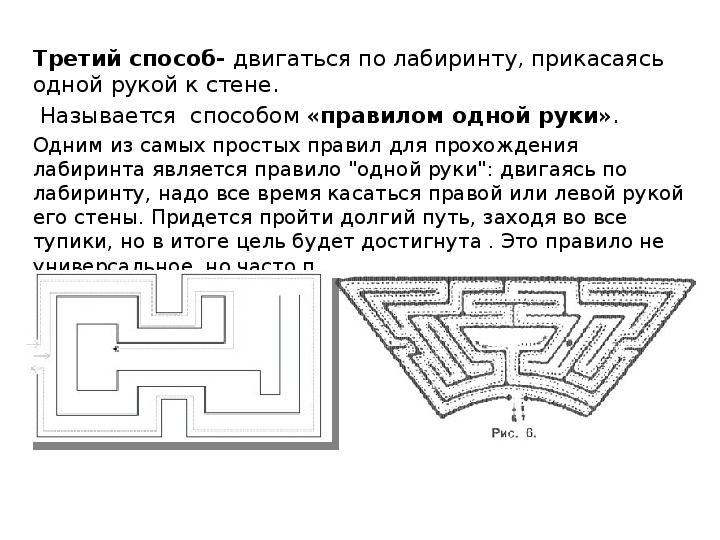
Поход DFS подобен прогулке по лабиринту. Вы исследуете путь, пока не достигните его конечной точки, после чего возвращаетесь и идёте другим.
Здесь для наглядной демонстрации этого принципа мы используем простое бинарное дерево. Начиная от исходного узла А, мы двигаемся к смежному узлу B, а затем к D, где оказываемся в самом удалённой точке. Затем мы возвращаемся на шаг назад к B и переходим к следующему смежному узлу — E.
Давайте разобьём все наши действия на шаги. Сначала мы инициализируем стек и массив “visited” (посещённые узлы).
Добавляем корневой узел А в стек.
Помечаем узел A как посещённый и смотрим, есть ли среди смежных с ним узлов непосещённые. Есть два таких узла, помещаем их в стек и далее выбираем любой из них. Здесь будем следовать алфавитному порядку.
Помечаем B как посещённый и далее смотрим, есть ли у него соседи, которых мы ещё не посетили. Их два — D и E. Добавляем их в стек.
Посещаем D и отмечаем его. У этого узла нет непосещённых соседей, поэтому в стек ничего не добавляем.
Проверяем верхушку стека и через возврат к предыдущему узлу посещаем E. Затем также проверяем наличие непосещённых соседей у него.
Поскольку таких соседей у этого узла нет, мы продолжаем освобождать стек, пока не найдём узел с новыми непосещёнными соседями. В этом случае такового нет, поэтому стек в итоге освобождается полностью.
Преимущества:
- DFS в отношении бинарного дерева обычно требует меньше памяти, чем BFS.
- DFS легко реализовать через рекурсию.
Недостатки:
- В отличие от поиска в ширину DFS не всегда находит ближайший путь к искомому узлу.
DFS в Python
Дерево в коде мы представляем, используя список смежности через словарь Python. Для каждой вершины есть список смежных ей узлов.
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : [],
'D' : [],
'E' : []
}Далее мы определяем отслеживание посещённых узлов через инструкцию visited = set().
Взяв за основу список смежности и начав с узла A, мы можем найти все узлы дерева, применяя рекурсивную функцию DFS. Алгоритм функции dfs:
1. Проверяем, посещён ли текущий узел. Если да, то он добавляется в соответствующий набор.
2. Функция повторно вызывается для каждого соседа узла.
3. Базовый case вызывается, когда все узлы уже посещены, и после этого функция делает возврат.
def dfs(visited, graph, node):
if node not in visited:
print (node)
visited.add(node)
for neighbor in graph[node]:
dfs(visited, graph, neighbor)
В этом подходе мы выполняем поиск по всем узлам дерева, создавая широкую сеть. Это означает, что сначала мы обходим один уровень потомков и лишь затем переходим к последующему уровню уже их потомков.
Такой поиск сначала изучает ближайшие узлы и затем переходит всё дальше в сторону от исходной точки. С учётом этого мы хотим работать со структурой данных, которая при необходимости даёт самый старший элемент, считая их по порядку добавления. Здесь нам нужно применить механизм “очереди”.
Посмотрим, как очереди помогут нам с реализацией BFS и увидим работу BFS в бинарном дереве. Начиная от исходного узла A, мы продолжаем по порядку исследовать ветки, а именно переходим сначала к B, а затем к C, на котором текущий уровень завершается. После мы спускаемся на следующий уровень и посещаем D, откуда следуем к E.
Сначала мы инициализируем очередь и массив “visited”.
Начинаем с посещения корневого узла A.
Отмечаем A как посещённый и переходим к смежным с ним непосещённым узлам. В данном примере это два узла — B и C, и мы добавляем их в очередь, следуя алфавитному порядку.
Далее мы отмечаем B как посещённый и добавляем в очередь его потомков — D и E.
Теперь переходим к С, у которого нет непосещённых соседей.
Далее, спустившись на уровень вниз, мы посещаем сначала D, а потом E, также продолжая убирать каждый посещаемый узел из очереди. Программа завершится, когда в очереди не останется элементов.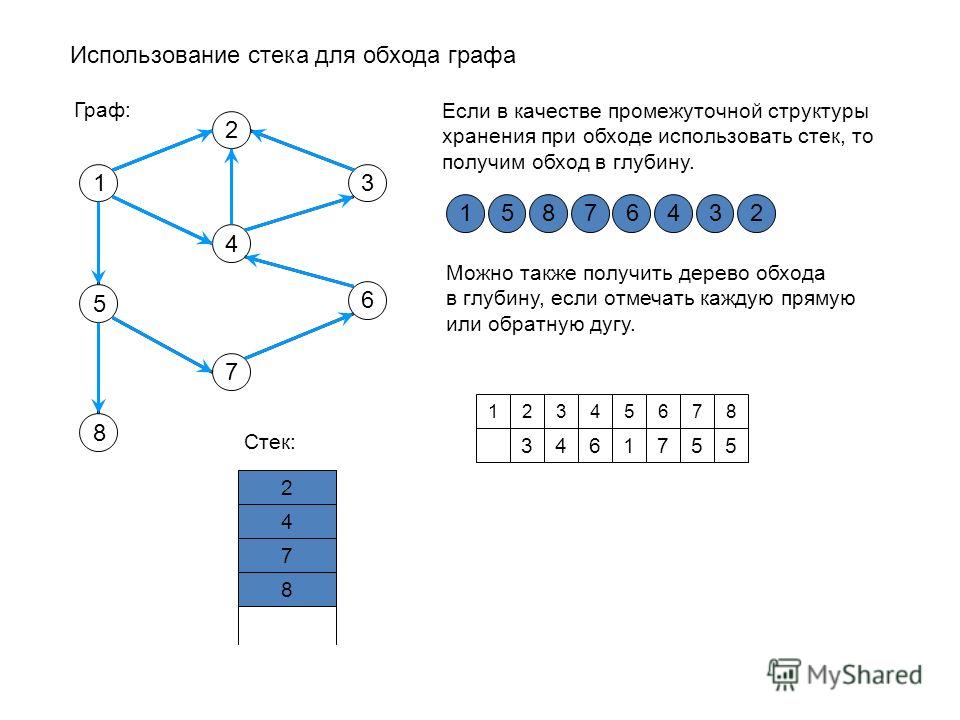
Преимущества:
- Легко реализовать.
- Можно применять в любой задаче поиска.
- В отличие от DFS не подвержен проблеме бесконечного цикла, которая может вызвать сбой компьютера при выполнении углублённого DFS-поиска.
- Всегда находит кратчайший путь при условии равного веса ссылок, в связи с чем считается полноценным и более оптимальным способом поиска.
Недостатки:
- BFS требует больше памяти.
- BFS — это так называемый “слепой” поиск, охватывающий огромную область, из-за чего производительность будет уступать другим аналогичным эвристическим методам.
BFS в Python
Дерево в коде мы также представляем, используя список смежности через словарь Python. Каждая вершина хранит список смежных с ней узлов.
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : [],
'D' : [],
'E' : []
}Далее для отслеживания посещённых узлов мы устанавливаем visited = [].
Для отслеживания узлов, находящихся в очереди, мы устанавливаем queue = [].
Учитывая список смежности и начиная от узла A, мы можем найти все узлы дерева, используя рекурсивную функцию bfs, которая:
- Сначала проверяет и добавляет стартовый узел в список посещённых, а также в очередь.
- Далее, пока в очереди присутствуют элементы, она продолжает исключать узлы, добавлять их непосещённых соседей и затем отмечать их как посещённых.
- Выполняет эти действия, пока очередь не опустеет.
def bfs(visited, graph, node):
visited.append(node)
queue.append(node)while queue:
s = queue.pop(0)
print (s, end = " ")for neighbor in graph[s]:
if neighbor not in visited:
visited.append(neighbor)
queue.append(neighbor)
Вот мы и рассмотрели отличия DFS и BFS. Вам наверняка также интересно узнать, когда и какой из них подходит лучше. На ранней стадии изучения алгоритмов я тоже задавался этим вопросом. Надеюсь, мой ответ сможет дать достаточное пояснение:
Надеюсь, мой ответ сможет дать достаточное пояснение:
- Если нам известно, что искомая точка находится недалеко от корня, то лучше использовать BFS.
- Если дерево имеет очень глубокую структуру, а искомые точки в нём редки, то DFS может потребовать очень много времени. BFS же справится быстрее.
- Если дерево очень широкое, то BFS может потребовать так много памяти, что утратит свою практичность.
- Если искомые точки встречаются часто, но расположены в глубине дерева, BFS может также оказаться непрактичным.
Обычно стоит использовать:
- BFS, когда нужно найти кратчайший путь от конкретного исходного узла к нужной точке. Иначе говоря, когда нас интересует путь с наименьшим числом шагов, ведущих от заданного начального состояния к искомому.
- DFS, когда нужно исследовать все возможности и найти наилучшую либо пересчитать количество возможных путей.
- BFS или DFS, когда нужно только проверить наличие связи между двумя узлами представленного графа или, иначе говоря, узнать, можем ли мы достичь одного, находясь в другом.
Мы изучили теорию и разобрались в двух популярных алгоритмах поиска — DFS и BFS. Помимо этого, теперь вы знаете, как реализовывать их в Python. Настало время применить все эти знания на практике. Не стоит откладывать, ведь это занятие будет уже куда интереснее чтения. Код BFS и DFS доступен на GitHub.
Читайте также:
Читайте нас в Telegram, VK и Яндекс.Дзен
Алгоритмы генерации лабиринтов
Лабиринты — это не только самостоятельный класс игр, но и основа для создания локаций в играх других жанров: например, систем пещер, которые, в свою очередь, могут быть использованы в очень широком классе игр-бродилок и т.д. Однако если игроку придется постоянно «изучать» одни и те же локации, ему это может скоро надоесть, а потому перед разработчиками игр встает вопрос о процедурной генерации лабиринтов, т.е. чтобы каждое очередное прохождение игры проходило на заново сгенерированной территории.
Таких алгоритмов существует уже очень много, поэтому представленная нами подборка не претендует на полноту — в комментариях вы можете поделиться ссылками на известные вам способы генерации лабиринтов.
Лабиринты мы будем строить на прямоугольном клеточном поле (+ одна из статей о генерации в трехмерном пространстве), поэтому все их можно разделить на две группы: лабиринты с «тонкими» стенками и с «толстыми». Первые — это те, у которых стены расположены на границах клеток, вторые — это те, в которых некоторые клетки сами являются непроходимыми, т.е. стенами. Их отличает, например, способ хранения данных о карте.
Также существуют уже готовые решения для генерации лабиринтов: генератор Oblige, который используется в DOOM, DOOM II и Heretic, и др.
Алгоритм Эллера
На тему генерации лабиринтов, где стенки расположены на границах клеток, на Хабре есть хороший перевод статьи «Eller’s Algorithm» (именно Эллера, а не Эйлера — «Eller’s», а не «Euler’s») о том, как создать идеальный (perfect) лабиринт — такой, что между любыми двумя его клетками существует путь, и притом единственный.
Общая идея алгоритма заключается в построчной генерации, где между каждыми двумя клетками строки при определенных условиях (чтобы не было циклов и недоступных клеток) случайным образом возникает стенка. При этом в конце все клетки окажутся «в одном множестве», что будет означать, что между каждыми двумя клетками существует путь.
Хранить карту лабиринта можно, например, в двух двумерных массивах: для вертикальных стенок и горизонтальных, соответственно.
Как хранить лабиринты с «толстыми» стенками?
Ответ на вопрос о хранении карт таких лабиринтов очевиден: в виде двумерного boolean массива, где, например, 1 — это непроходимая клетка (стена), 0 — свободная.
Подробнее о картах на клеточных полях написано в статье «Tilebased games». Теперь перейдем к самим лабиринтам генерации.
Наивный алгоритм
Начнем с самого очевидного алгоритма генерации — когда расположение комнат определяется случайным образом. Все, что нужно сделать — это задать граничные размеры комнат, их количество и границы поля, после чего случайным образом определять их координаты на карте и размеры. После чего просто соединить их коридорами.
Все, что нужно сделать — это задать граничные размеры комнат, их количество и границы поля, после чего случайным образом определять их координаты на карте и размеры. После чего просто соединить их коридорами.
Естественно, возникают два вопроса: не будут ли комнаты пересекаться и как проложить между ними переходы? Ответ на первый вопрос зависит от ваших требований к лабиринту: если вы не хотите, чтобы комнаты пересекались, напишите функцию, которая проверяет пару комнат на пересечение и при появлении на карте очередной комнаты делайте проверку.
Чтобы проложить коридоры между помещениями, автор предлагает сначала прокладывать переход от уровня одной комнаты до уровня другой по оси Oy, а затем так же по оси Ox — смотрите поясняющий рисунок.
Подробнее об этом алгоритме (с примерами реализации) читайте в статье «Сreate a Procedurally Generated Dungeon Cave System».
Лабиринт на таблице
У описанного выше алгоритма есть один явный недостаток: проверять, пересекаются ли комнаты, приходится отдельной функцией. Возникает вопрос, можно ли не делать это лишнее действие. Оказывается, можно— и алгоритм описан ниже.
Идея заключается в том, что поле изначально разбивается на прямоугольные «большие» клетки (т.е. не элементарные клетки игрового поля, а прямоугольники, состоящие из нескольких клеток), образуя таким образом таблицу. Далее в каждой такой ячейке случайным образом появляется комната случайного размера, не превосходящая размеров ячейки — тем самым возможность появления пересекающихся помещений пропадает. Затем комнаты объединяются коридорами, например, тем же способом, что описано в предыдущем пункте.
Подробно этот алгоритм генерации описан в статье «Grid Based Dungeon Generator».
BSP деревья
BSP — это аббревиатура от Binary Space Partitioning — двоичное разделение пространства. Этот алгоритм также позволяет избежать пересечения комнат еще в процессе помещения их на карту, т.к. также предварительно делит игровое поле на части — «листья», внутри которых затем генерирует комнаты. Это деление площади идейно сложнее, т.к. разделяет все , чем предыдущий алгоритм, но и позволяет создать более интересные конфигурации расположения помещений.
Это деление площади идейно сложнее, т.к. разделяет все , чем предыдущий алгоритм, но и позволяет создать более интересные конфигурации расположения помещений.
Почитать подробнее о нем можно в статье «How to Use BSP Trees to Generate Game Maps».
Генерация лабиринтов с использованием клеточного автомата
Каждый программист хотя бы раз писал «Жизнь» — клеточный автомат, придуманный математиком Конвэем. Так почему бы не использовать схожую идею для генерации лабиринтов? Суть предложенного алгоритма состоит в реализации всего двух шагов: сначала все поле заполняется случайным образом стенами — т.е. для каждой клетки случайным образом определяется, будет ли она свободной или непроходимой — а затем несколько раз происходит обновление состояния карты в соответствии с условиями, похожими на условия рождения/смерти в «Жизни».
В источнике — на странице статьи «Generate Random Cave Levels Using Cellular Automata» — вы можете поэкспериментировать с интерактивной демкой, устанавливая различные значения для генерации: количество итераций обновления, граничные значения для жизни/смерти клетки и т.п. — и увидеть результат. Там же рассказывается о подводных камнях реализации.
Генерация в трехмерном пространстве
Также мы не можем оставить без внимания статью о генерации 3D-лабиринтов: «Bake Your Own 3D Dungeons With Procedural Recipes» — основная сложность которого заключается в правильной ориентации элементарных частей лабиринта: коридоров, комнат и лестниц.
Каждый из модулей хранит информацию о своих входах и выходах, а также их ориентации: прежде чем соединить очередную пару элементарных частей, их нужно правильно ориентировать. В частности, автор предлагает хранить x-, y- и z- ориентацию модулей, чтобы затем соединять их по таким правилам: их y-оси должны совпадать, а x и z — иметь противоположное направление. Это, естественно, ставит вопрос о хранении информации о сгенерированной карте. Кроме того, не решена проблема с пересечением помещений — поэтому эта статья может являться лишь отправной точкой для исследования вопросов генерации трехмерных алгоритмов.
Что дальше?
На тему этой статьи существует огромное множество материалов, которые могут быть найдены в интернете, поэтому если вы хотите углубиться в изучение вопроса генерации лабиринтов, можете заглянуть сначала сюда, а потом уж, конечно же, вот сюда.
Спасибо за внимание!
Лабиринты: классификация, генерирование, поиск решений
Лабиринты в целом (а значит, и алгоритмы для их создания) можно разбить по семи различным классификациям: размерности, гиперразмерности, топологии, тесселяции, маршрутизации, текстуре и приоритету. Лабиринт может использовать по одному элементу из каждого класса в любом сочетании.
класс размерности по сути определяет, сколько измерений в пространстве заполняет лабиринт. Существуют следующие типы:
классификация по гиперразмерности соответствует размерности объекта, двигающегося через лабиринт, а не самого лабиринта. Существуют следующие типы:
класс топологии описывает геометрию пространства лабиринта, в котором тот существует как целое. Есть следующие типы:
классификация геометрии отдельных ячеек, из которых состоит лабиринт. Существующие типы:
классификация по маршрутизации — это, вероятно, наиболее интересный аспект в генерации лабиринтов. От связан с типами проходов в пределах геометрии, определённой в описанных выше категориях.
классификация по текстуре описывает стиль проходов при различной маршрутизации и геометрии. Текстура — это не просто параметры, которые можно включать или выключать. Вот несколько примеров переменных:
эта классификация показывает, что процессы создания лабиринтов можно разделить на два основных типа: добавляющие стены и вырезающие проходы. Обычно при генерации это сводится только к разнице в алгоритмах, а не к заметным отличиям лабиринтов, но всё равно это полезно учитывать. Один и тот же лабиринт часто генерируется обоими способами:
описанное выше ни в коем случае не является исчерпывающим списком всех возможных классов или элементов внутри каждого класса. Это только те типы лабиринтов, которые я создавал сам. Заметьте, что почти каждый тип лабиринта, в том числе и лабиринты с особыми правилами, можно выразить в виде ориентированного графа, в котором будет конечное количество состояний и конечное количество вариантов выбора в каждом состоянии, и это называется
Это только те типы лабиринтов, которые я создавал сам. Заметьте, что почти каждый тип лабиринта, в том числе и лабиринты с особыми правилами, можно выразить в виде ориентированного графа, в котором будет конечное количество состояний и конечное количество вариантов выбора в каждом состоянии, и это называется
. Вот несколько других классификаций и типов лабиринтов:
Вот список обобщённых алгоритмов для создания различных классов лабиринтов, описанных выше:
Идеальный: для создания стандартного идеального лабиринта обычно необходимо «выращивать» его, обеспечив отсутствие петель и изолированных областей. Начинаем с внешней стены и случайным образом добавляем касающийся её фрагмент стены. Продолжаем случайным образом добавлять в лабиринт сегменты стен, но проверяем, что каждый новый сегмент касается с одного конца существующей стены, а его другой конец находится в ещё несозданной части лабиринта. Если вы добавляете сегмент стены, оба конца которого отделены от остального лабиринта, то это создаст несоединённую стену с петлёй вокруг, а если добавить сегмент, оба конца которого касаются лабиринта, то это создать недостижимую область. Это метод добавления стен; почти аналогично ему вырезание проходов, при котором части проходов вырезаются таким образом, чтобы существующего прохода касался только один конец.
Плетёный: для создания лабиринта без тупиков по сути нужно добавлять в лабиринт сегменты стен случайным образом, но делать так, чтобы каждый новый добавляемый сегмент не приводил к созданию тупика. Я создаю их за четыре этапа: (1) начинаю с внешней стены, (2) обхожу лабиринт и добавляю отдельные сегменты стены, касающиеся каждой вершины стены, чтобы в лабиринте не было открытых комнат или небольших стен-«столбов», (3) обхожу все возможные сегменты стен в случайном порядке, добавляя стену там, где она не создаст тупика, (4) или запускаю процедуру удаления изолированных областей в конце, чтобы лабиринт был правильным и имел решение, или поступаю умнее на этапе (3) и делаю так, чтобы стена добавлялась только тогда, когда она не может привести к изолированной области.
Одномаршрутный: один из способов создания случайного одномаршрутного лабиринта — создать идеальный лабиринт, закрыть выход, чтобы остался только один вход, а затем добавлять стены, разделяющие каждый проход на две части. Это превращает каждый тупик в U-образный поворот, и у нас получится одномаршрутный проход, начинающийся и заканчивающийся в начале исходного лабиринта, который будет следовать по тому же пути, как и перемещение вдоль стены исходного лабиринта. Новый одномаршрутный лабиринт будет иметь удвоенный относительно исходного идеального лабиринта размер. Можно добавить небольшие хитрости, чтобы начало и конец не всегда находились друг рядом с другом: при создании идеального лабиринта мы никогда не будем добавлять сегменты, соединяющиеся с правой или нижней стенами, поэтому получившийся лабиринт будет иметь простое решение, следующее вдоль стены. Поставим вход в правом верхнем углу, и после разбиения пополам для создания одного маршрута удалим правую и нижнюю стены. В результате получится одномаршрутный лабиринт, начинающийся в правом верхнем углу и заканчивающийся в левом нижнем.
Разреженный: разреженные лабиринты создаются решением не выращивать лабиринт в областях, которые будут нарушать правило разреженности. Для целостной реализации этого нужно при выборе новой вырезаемой ячейки сначала проверять все ячейки, находящиеся в полукруге выбранного радиуса ячеек, расположенных впереди от текущего направления. Если какая-то из этих ячеек уже является частью лабиринта, то мы не позволяем рассматривать эти ячейки, потому что в противном случае они будут слишком близко к существующей ячейке, а значит, превратят лабиринт в неразреженный.

Переплетённый: переплетённые лабиринты по сути создаются как идеальные лабиринты с вырезанием проходов, только при вырезании проходов мы не всегда ограничены существующим проходом, потому что у нас есть возможность пройти под ним и всё равно сохранить идеальность лабиринта. В монохромном растровом изображении переплетённый лабиринт можно представить четырьмя строками на проход (двух строк на проход достаточно для стандартного идеального лабиринта): одна строка для самого прохода, а остальные три строки недвусмысленно показывают, когда другой соседний проход идёт под ним, а не просто образует тупик рядом с первым проходом. Ради эстетичности перед вырезанием под уже готовым проходом можно заглядывать вперёд, чтобы убедиться. что можно продолжить вырезание, находясь под ним; так можно избежать тупиков, расположенных прямо под другими проходами. Также после вырезания под проходом можно инвертировать соседние с пересечением пиксели, чтобы новые проходы проходили над старыми, а не под ними.
Crack: Crack-лабиринты по сути создаются как идеальные лабиринты с добавлением стен, только в них нет отчётливой тесселяции, за исключением случайного расположения пикселей. Выбираем пиксель, который уже поставлен как стена, выбираем ещё одну случайную локацию, и «стреляем» или начинаем рисовать стену в сторону второй локации. Однако нужно останавливаться, не доходя до уже существующих стен, чтобы не создать изолированности. Завершаем работу, если какое-то время не можем добавить новых значимых стен. Учтите, что случайные локации для рисования могут находится в любом месте лабиринта, поэтому по лабиринту будет проходить несколько прямых линий и множество пропорционально меньших стен; количество стен ограничено только пиксельным разрешением. Это делает лабиринт очень похожим на поверхность листа, то есть по сути это фрактальный лабиринт.
Омега: для лабиринтов в стиле «омега» необходимо задать некую сетку, способ соединения ячеек друг с другом и привязку к экрану вершин, окружающих каждую ячейку. Например, для треугольного дельта-лабиринта с соединяющимися треугольными ячейками: (1) есть сетка, в которой количество ячеек в каждой следующей строке увеличивается на две. (2) Каждая ячейка соединяется с ячейками, соседними с ней в этом ряду, за исключением третьего прохода, который соединён с соответствующей ячейкой строкой выше или ниже, в зависимости от того, нечётный или чётный этот столбец (т.е. смотрил ли треугольник вверх или вниз). (3) Каждая ячейка использует математику треугольников, чтобы определить, где отрисовывать его на экране. Можно заранее отрисовать все стены на экране и вырезать в лабиринте проходы, или хранить в памяти некий изменяемый массив и рендерить всё после завершения.
Например, для треугольного дельта-лабиринта с соединяющимися треугольными ячейками: (1) есть сетка, в которой количество ячеек в каждой следующей строке увеличивается на две. (2) Каждая ячейка соединяется с ячейками, соседними с ней в этом ряду, за исключением третьего прохода, который соединён с соответствующей ячейкой строкой выше или ниже, в зависимости от того, нечётный или чётный этот столбец (т.е. смотрил ли треугольник вверх или вниз). (3) Каждая ячейка использует математику треугольников, чтобы определить, где отрисовывать его на экране. Можно заранее отрисовать все стены на экране и вырезать в лабиринте проходы, или хранить в памяти некий изменяемый массив и рендерить всё после завершения.
Гиперлабиринт: гиперлабиринт — это 3D-среда, похожая на обратную версию стандартного трёхмерного не-гиперлабиринта, в котором блоки становятся открытыми пространствами, и наоборот. Хотя стандартный 3D-лабиринт состоит из дерева проходов через сплошную площадь, гиперлабиринт состоит из дерева полос или лиан, проходящих по открытой площади. Для создания гиперлабиринта мы начинаем со сплошных верхней и нижней граней, а затем выращиваем извилистые лианы из этих граней для заполнения пространства между ними, чтобы усложнить прохождение отрезка прямой между этими двумя гранями. Если каждая лиана соединяется с верхней или нижней частью, то гиперлабиринт будет иметь хотя бы одно простое решение. Если ни одна лиана не соединяется и с верхней, и с нижней частями (что создаст непроходимый столбец), то пока в верхней и нижней частях нет петель лиан, которые заставляют их неразрывно соединяться друг с другом подобно цепи, гиперлабиринт будет оставаться решаемым.
Planair: Planair-лабиринты с необычной топологией обычно создаются как массив из одного или нескольких лабиринтов или частей лабиринтов, в которых определён способ соединения краёв друг с другом. Лабиринт на поверхности куба — это всего лишь шесть квадратных частей лабиринта. Когда создаваемая часть доходит до края, то она перетекает в следующую часть и в правый край.
Когда создаваемая часть доходит до края, то она перетекает в следующую часть и в правый край.
Шаблон: лабиринты, основанные на шаблонах, создаются, начиная с базового изображения-шаблона, а затем запускается устранитель изолированных областей, обеспечивающий наличие решения лабиринта, за которым следует устранитель петель, повышающий сложность лабиринта. В результате создаётся идеальный лабиринт, очень похожий на исходное изображение. Например, для создания лабиринта, состоящего из пересекающихся спиралей нужно просто создать случайные спирали, не волнуясь о том, являются ли они лабиринтом, а затем пропустить их через устранители изолированных областей и петель.
Существует множество способов создания идеальных лабиринтов, и каждый из них имеет собственные характеристики. Ниже представлен список конкретных алгоритмов. Во всех них описано создание лабиринта вырезанием проходов, однако если не указано иное, каждый также можно реализовать добавлением стен:
Recursive backtracker: он в чём-то похож на метод решения лабиринтов recursive backtracker, и требует стека, объём которого может доходить до размеров лабиринта. При вырезании он ведёт себя максимально жадно, и всегда вырезает проход в несозданной части, если она существует рядом с текущей ячейкой. Каждый раз, когда мы перемещаемся к новой ячейке, записываем предыдущую ячейку в стек. Если рядом с текущей позицией нет несозданных ячеек, то извлекаем из стека предыдущую позицию. Лабиринт завершён, когда в стеке больше ничего не остаётся. Это приводит к созданию лабиринтов с максимальным показателем текучести, тупиков меньше, но они длиннее, а решение обычно оказывается очень долгим и извилистым. При правильной реализации он выполняется быстро, и быстрее работают только очень специализированные алгоритмы. Recursive backtracking не может работать с добавлением стен, потому что обычно приводит к пути решения, следующему по внешнему краю, когда вся внутренняя часть лабиринта соединена с границей одним проходом.
Алгоритм Краскала: это алгоритм, создающий минимальное связующее дерево. Это интересно, потому что он не «выращивает» лабиринт подобно дереву, а скорее вырезает сегменты проходов по всему лабиринту случайным образом, и тем не менее в результате создаёт в конце идеальный лабиринт. Для его работы требуется объём памяти, пропорциональный размеру лабиринта, а также возможность перечисления каждого ребра или стены между ячейками лабиринта в случайном порядке (обычно для этого создаётся список всех рёбер и перемешивается случайным образом). Помечаем каждую ячейку уникальным идентификатором, а затем обходим все рёбра в случайном порядке. Если ячейки с обеих сторон от каждого ребра имеют разные идентификаторы, то удаляем стену и задаём всем ячейкам с одной стороны тот же идентификатор, что и ячейкам с другой. Если ячейки на обеих сторонах стены уже имеют одинаковый идентификатор, то между ними уже существует какой-то путь, поэтому стену можно оставить, чтобы не создавать петель. Этот алгоритм создаёт лабиринты с низким показателем текучести, но не таким низким, как у алгоритма Прима. Объединение двух множество по обеим сторонам стены будет медленной операцией, если у каждой ячейки есть только номер и они объединяются в цикле. Объединение, а также поиск можно выполнять почти за постоянное время благодаря использованию алгоритма объединения-поиска (union-find algorithm): помещаем каждую ячейку в древовидную структуру, корневым элементом является идентификатор. Объединение выполняется быстро благодаря сращиванию двух деревьев. При правильной реализации этот алгоритм работает достаточно быстро, но медленнее большинства из-за создания списка рёбер и управления множествами.
Алгоритм Прима (истинный): этот алгоритм создаёт минимальное связующее дерево, обрабатывая уникально случайные веса рёбер. Объём требуемой памяти пропорционален размеру лабиринта. Начинаем с любой вершины (готовый лабиринт будет одинаковым, с какой бы вершины мы ни начали).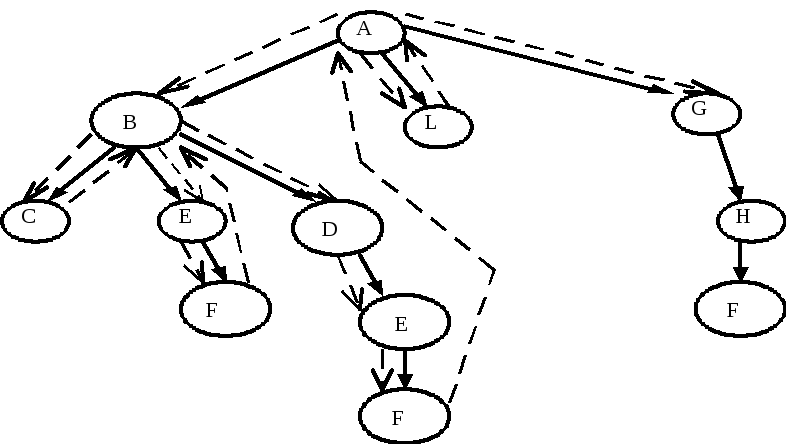 Выполняем выбор ребра прохода с наименьшим весом, соединяющим лабиринт к точке, которая ещё в нём не находится, а затем присоединяем её к лабиринту. Создание лабиринта завершается, когда больше не осталось рассматриваемых рёбер. Для эффективного выбора следующего ребра необходима очередь с приоритетом (обычно реализуемая с помощью кучи), хранящая все рёбра границы. Тем не менее, этот алгоритм достаточно медленный, потому что для выбора элементов из обработка кучи требует времени log(n). Поэтому лучше предпочесть алгоритм Краскала, который тоже создаёт минимальное связующее дерево, ведь он быстрее и создаёт лабиринты с идентичной структурой. На самом деле при одинаковом случайном seed алгоритмами Прима и Краскала можно создавать одинаковые лабиринты.
Выполняем выбор ребра прохода с наименьшим весом, соединяющим лабиринт к точке, которая ещё в нём не находится, а затем присоединяем её к лабиринту. Создание лабиринта завершается, когда больше не осталось рассматриваемых рёбер. Для эффективного выбора следующего ребра необходима очередь с приоритетом (обычно реализуемая с помощью кучи), хранящая все рёбра границы. Тем не менее, этот алгоритм достаточно медленный, потому что для выбора элементов из обработка кучи требует времени log(n). Поэтому лучше предпочесть алгоритм Краскала, который тоже создаёт минимальное связующее дерево, ведь он быстрее и создаёт лабиринты с идентичной структурой. На самом деле при одинаковом случайном seed алгоритмами Прима и Краскала можно создавать одинаковые лабиринты.
Алгоритм Прима (упрощённый): этот алгоритм Прима создаёт минимальное связующее дерево. Он упрощён таким образом, что все веса рёбер одинаковы. Для него требуется объём памяти, пропорциональный размеру лабиринта. Начинаем со случайной вершины. Выбираем случайным образом ребро прохода, соединяющее лабиринт с точкой, которая ещё не в нём, а затем присоединяем её к лабиринту. Лабиринт оказывается завершённым, когда больше не остаётся рассматриваемых рёбер. Так как рёбра не имеют веса и не упорядочены, их можно хранить как простой список, то есть выбор элементов из списка будет очень быстрым и занимает постоянное время. Поэтому он намного быстрее истинного алгоритма Прима со случайными весами рёбер. Создаваемая текстура лабиринта будет иметь меньший показатель текучести и более простое решение, чем у истинного алгоритма Прима, потому что распространяется из начальной точки равномерно, как пролитый сироп, а не обходит фрагменты рёбер с более высоким весом, которые учитываются позже.
Алгоритм Прима (модифицированный): этот алгоритм Прима создаёт минимальное связующее дерево, изменённое так, что все веса рёбер одинаковы. Однако он реализован таким образом, что вместо рёбер смотрит на ячейки. Объём памяти пропорционален размеру лабиринта. В процессе создания каждая ячейка может иметь один из трёх типов: (1) «внутренняя»: ячейка является частью лабиринта и уже вырезана в нём, (2) «граничная»: ячейка не является частью лабиринта и ещё не вырезана в нём, но находится рядом с ячейкой, которая уже является «внутренней», и (3) «внешняя»: ячейка ещё не является часть лабиринта, и ни один из её соседей тоже не является «внутренней» ячейкой. Начинаем с выбора ячейки, делаем её «внутренней», а для всех её соседей задаём тип «граничная». Выбираем случайным образом «граничную» ячейку и вырезаем в неё проход из одной из соседних «внутренних» ячеек. Меняем состояние этой «граничной» ячейки на «внутреннюю» и изменяем тип всех её соседей с «внешней» на «граничную». Лабиринт завершён, когда больше не остаётся «граничных» ячеек (то есть не осталось и «внешних» ячеек, а значит, все стали «внутренними»). Этот алгоритм создаёт лабиринты с очень низким показателем текучести, имеет множество коротких тупиков и довольно прямолинейное решение. Полученный лабиринт очень похож на результат упрощённого алгоритма Прима, за незначительным отличием: пустоты в связующем дереве заполняются, только если случайным образом выбирается граничная ячейка, в отличие от утроенной вероятности заполнения этой ячейки через одну из граничных ячеек, ведущих в неё. Кроме того, алгоритм очень быстр, быстрее упрощённого алгоритма Прима, потому что ему не нужно составлять и обрабатывать список рёбер.
Объём памяти пропорционален размеру лабиринта. В процессе создания каждая ячейка может иметь один из трёх типов: (1) «внутренняя»: ячейка является частью лабиринта и уже вырезана в нём, (2) «граничная»: ячейка не является частью лабиринта и ещё не вырезана в нём, но находится рядом с ячейкой, которая уже является «внутренней», и (3) «внешняя»: ячейка ещё не является часть лабиринта, и ни один из её соседей тоже не является «внутренней» ячейкой. Начинаем с выбора ячейки, делаем её «внутренней», а для всех её соседей задаём тип «граничная». Выбираем случайным образом «граничную» ячейку и вырезаем в неё проход из одной из соседних «внутренних» ячеек. Меняем состояние этой «граничной» ячейки на «внутреннюю» и изменяем тип всех её соседей с «внешней» на «граничную». Лабиринт завершён, когда больше не остаётся «граничных» ячеек (то есть не осталось и «внешних» ячеек, а значит, все стали «внутренними»). Этот алгоритм создаёт лабиринты с очень низким показателем текучести, имеет множество коротких тупиков и довольно прямолинейное решение. Полученный лабиринт очень похож на результат упрощённого алгоритма Прима, за незначительным отличием: пустоты в связующем дереве заполняются, только если случайным образом выбирается граничная ячейка, в отличие от утроенной вероятности заполнения этой ячейки через одну из граничных ячеек, ведущих в неё. Кроме того, алгоритм очень быстр, быстрее упрощённого алгоритма Прима, потому что ему не нужно составлять и обрабатывать список рёбер.
Алгоритм Олдоса-Бродера: интересно в этом алгоритме то, что он однородный, то есть он с равной вероятностью создаёт все возможные лабиринты заданного размера. Кроме того, ему не требуется дополнительной памяти или стека. Выбираем точку и случайным образом перемещаемся в соседнюю ячейку. Если мы попали в невырезанную ячейку, то вырезаем в неё проход из предыдущей ячейки. Продолжаем двигаться в соседние ячейки, пока не вырежем проходы во все ячейки. Этот алгоритм создаёт лабиринты с низким показателем текучести, всего немного выше, чем у алгоритма Краскала. (Это значит, что для заданного размена существует больше лабиринтов с низким показателем текучести, чем с высоким, потому что лабиринт со средней равной вероятностью имеет низкий показатель.) Плохо в этом алгоритме то, что он очень медленный, так как не выполняет интеллектуального поиска последних ячеек, то есть по сути не имеет гарантий завершения. Однако из-за своей простоты он может быстро проходить по множеству ячеек, поэтому завершается быстрее, чем можно было бы подумать. В среднем его выполнение занимает в семь раз больше времени, чем у стандартных алгоритмов, хотя в плохих случаях оно может быть намного больше, если генератор случайных чисел постоянно избегает последних нескольких ячеек. Он может быть реализован как добавляющий стены, если стену границы считать единой вершиной, т.е., например, если ход перемещает нас к стене границы, мы телепортируемся к случайной точке вдоль границы, а уже потом продолжаем двигаться. В случае добавления стен он работает почти в два раза быстрее, потому что телепортация вдоль стены границы позволяет быстрее получать доступ к дальним частям лабиринта.
(Это значит, что для заданного размена существует больше лабиринтов с низким показателем текучести, чем с высоким, потому что лабиринт со средней равной вероятностью имеет низкий показатель.) Плохо в этом алгоритме то, что он очень медленный, так как не выполняет интеллектуального поиска последних ячеек, то есть по сути не имеет гарантий завершения. Однако из-за своей простоты он может быстро проходить по множеству ячеек, поэтому завершается быстрее, чем можно было бы подумать. В среднем его выполнение занимает в семь раз больше времени, чем у стандартных алгоритмов, хотя в плохих случаях оно может быть намного больше, если генератор случайных чисел постоянно избегает последних нескольких ячеек. Он может быть реализован как добавляющий стены, если стену границы считать единой вершиной, т.е., например, если ход перемещает нас к стене границы, мы телепортируемся к случайной точке вдоль границы, а уже потом продолжаем двигаться. В случае добавления стен он работает почти в два раза быстрее, потому что телепортация вдоль стены границы позволяет быстрее получать доступ к дальним частям лабиринта.
Алгоритм Уилсона: это усовершенствованная версия алгоритма Олдоса-Бродера, он создаёт лабиринты точно с такой же текстурой (алгоритмы однородны, то есть все возможные лабиринты генерируются с равной вероятностью), однако алгоритм Уилсона выполняется гораздо быстрее. Он занимает память вплоть до размеров лабиринта. Начинаем со случайно выбранной начальной ячейки лабиринта. Выбираем случайную ячейку, которая ещё не является частью лабиринта и выполняем случайный обход, пока не найдём ячейку, уже принадлежащую лабиринту. Как только мы наткнёмся на уже созданную часть лабиринта,, возвращаемся к выбранной случайной ячейке и вырезаем весь проделанный путь, добавляя эти ячейки к лабиринту. Конкретнее, при возврате по пути мы в каждой ячейке выполняем вырезание в том направлении, в котором проходил случайный обход при последнем выходе из ячейки. Это позволяет избежать появления петель вдоль пути возврата, благодаря чему к лабиринту присоединяется один длинный проход.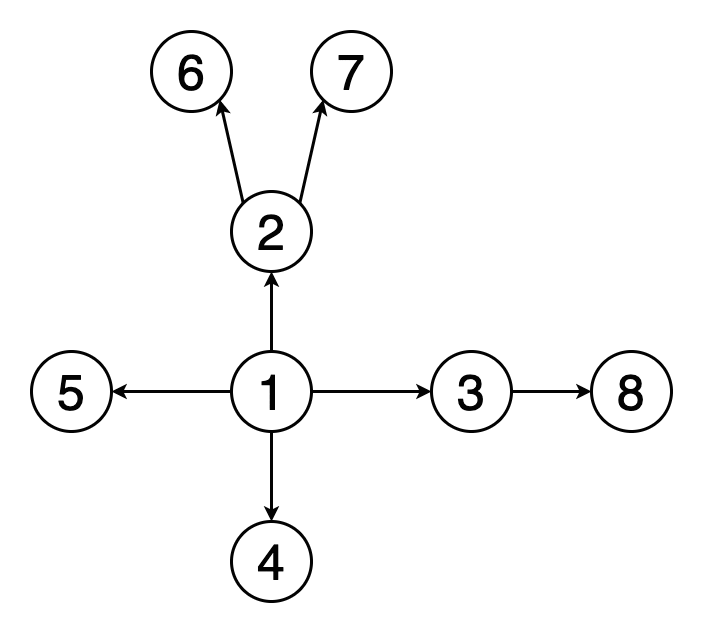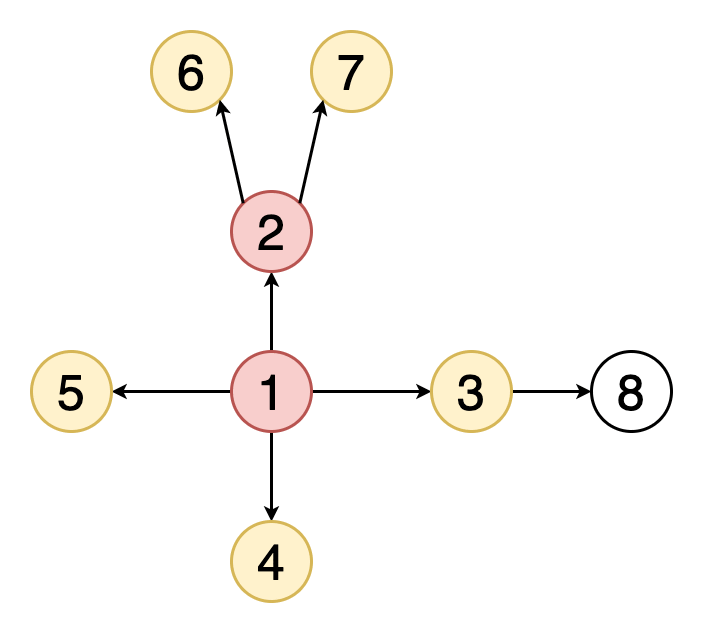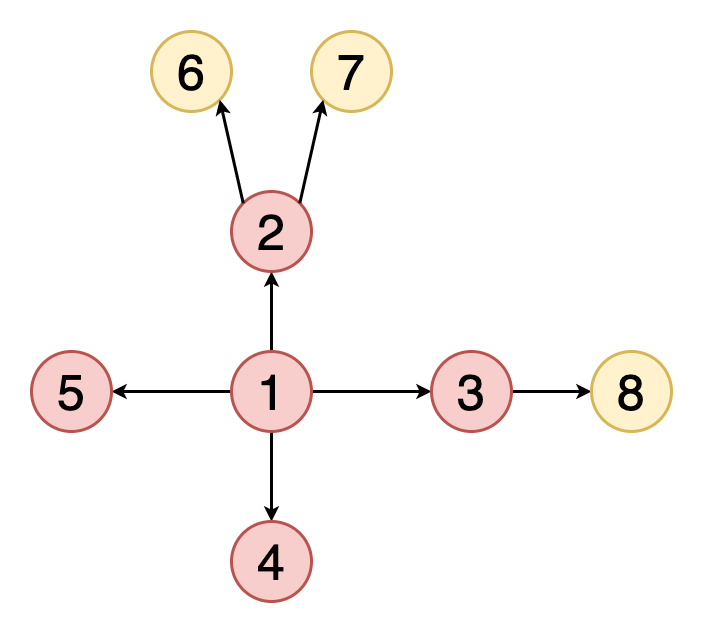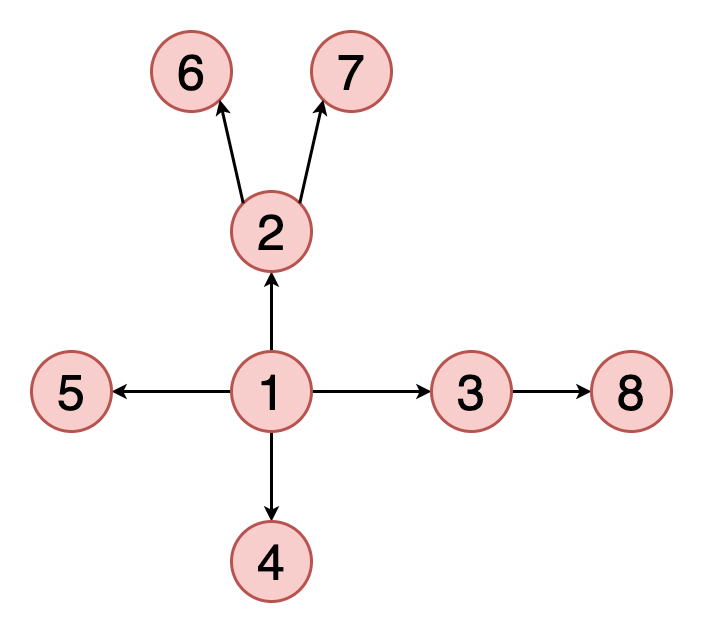 Лабиринт завершён, когда к нему присоединены все ячейки. Алгоритм имеет те же проблемы со скоростью, что и Олдос-Бродер, потому что может уйти много времени на нахождение первого случайного пути к начальной ячейке, однако после размещения нескольких путей остальная часть лабиринта вырезается довольно быстро. В среднем он выполняется в пять раз быстрее Олдоса-Бродера, и менее чем в два раза медленнее лучших алгоритмов. Стоит учесть, что в случае добавления стен он работает в два раза быстрее, потому что вся стена границы изначально является частью лабиринта, поэтому первые стены присоединяются гораздо быстрее.
Лабиринт завершён, когда к нему присоединены все ячейки. Алгоритм имеет те же проблемы со скоростью, что и Олдос-Бродер, потому что может уйти много времени на нахождение первого случайного пути к начальной ячейке, однако после размещения нескольких путей остальная часть лабиринта вырезается довольно быстро. В среднем он выполняется в пять раз быстрее Олдоса-Бродера, и менее чем в два раза медленнее лучших алгоритмов. Стоит учесть, что в случае добавления стен он работает в два раза быстрее, потому что вся стена границы изначально является частью лабиринта, поэтому первые стены присоединяются гораздо быстрее.
Алгоритм Hunt and kill: этот алгоритм удобен, потому что не требует дополнительной памяти или стека, а потому подходит для создания огромных лабиринтов или лабиринтах на слабых компьютерах благодаря невозможности исчерпания памяти. Так как в нём нет правил, которым нужно следовать постоянно, его также проще всего модифицировать и создавать с его помощью лабиринты с разной текстурой. Он почти схож с recursive backtracker, только рядом с текущей позицией нет несозданной ячейки. Мы входим в режим «охоты» и систематично сканируем лабиринт, пока не найдём несозданную ячейку рядом с уже вырезанной ячейкой. На этом этапе мы снова начинаем вырезание в этой новой локации. Лабиринт завершён, когда в режиме «охоты» просканированы все ячейки. Этот алгоритм склонен к созданию лабиринтов с высоким показателем текучести, но не таким высоким, как у recursive backtracker. Можно заставить его генерировать лабиринты с более низким показателем текучести, чаще входя в режим «охоты». Он выполняется медленнее из-за времени, потраченного на охоту за последними ячейками, но не намного медленее, чем алгоритм Краскала. Его можно реализовать по принципу добавления стен, если время от времени случайным образом телепортироваться, чтобы избежать проблем, свойственных recursive backtracker.
Алгоритм выращивания
дерева (Growing tree algorithm): это обобщённый алгоритм, способный создавать лабиринты с разной текстурой. Требуемая память может достигать размера лабиринта. При каждом вырезании ячейки мы добавляем её в список. Выбираем ячейку из списка и вырезаем проход в несозданную ячейку рядом с ней. Если рядом с текущей нет несозданных ячеек, удаляем текущую ячейку из списка. Лабиринт завершён, когда в списке больше ничего нет. Интересно в алгоритме то, что в зависимости от способа выбора ячейки из списка можно создавать множество разных текстур. Например, если всегда выбирать последнюю добавленную ячейку, то этот алгоритм превращается в recursive backtracker. Если всегда выбирать ячейки случайно, то он ведёт себя похоже, но не идентично алгоритму Прима. Если всегда выбирать самые старые ячейки, добавленные в список, то мы создадим лабиринт с наименьшим возможным показателем текучести, даже ниже, чем у алгоритма Прима. Если обычно выбирать самую последнюю ячейку, но время от времени выбирать случайную ячейку, то лабиринт будет иметь высокий показатель текучести, но короткое и прямое решение. Если случайно выбирать одну из самых последних ячеек, то лабиринт будет иметь низкий показатель текучести, но долгое и извилистое решение.
Требуемая память может достигать размера лабиринта. При каждом вырезании ячейки мы добавляем её в список. Выбираем ячейку из списка и вырезаем проход в несозданную ячейку рядом с ней. Если рядом с текущей нет несозданных ячеек, удаляем текущую ячейку из списка. Лабиринт завершён, когда в списке больше ничего нет. Интересно в алгоритме то, что в зависимости от способа выбора ячейки из списка можно создавать множество разных текстур. Например, если всегда выбирать последнюю добавленную ячейку, то этот алгоритм превращается в recursive backtracker. Если всегда выбирать ячейки случайно, то он ведёт себя похоже, но не идентично алгоритму Прима. Если всегда выбирать самые старые ячейки, добавленные в список, то мы создадим лабиринт с наименьшим возможным показателем текучести, даже ниже, чем у алгоритма Прима. Если обычно выбирать самую последнюю ячейку, но время от времени выбирать случайную ячейку, то лабиринт будет иметь высокий показатель текучести, но короткое и прямое решение. Если случайно выбирать одну из самых последних ячеек, то лабиринт будет иметь низкий показатель текучести, но долгое и извилистое решение.
Алгоритм выращивания леса (Growing forest algorithm): это более обобщённый алгоритм, сочетающий в себе типы, основанные на деревьях и множествах. Он является расширением алгоритма выращивания дерева, по сути включающего в себя несколько экземпляров, расширяющихся одновременно. Начинаем со всех ячеек, случайным образом отсортированных в список «новых»; кроме того, у каждой ячейки есть собственное множество, как в начале алгоритма Краскала. Сначлаа выбираем одну или несколько ячеек, перемещая их из списка «новых» в список «активных». Выбираем ячейку из «активного» списка и вырезаем проход в соседнюю несозданную ячейку из «нового» списка, добавляя новую ячейку в список «активных» и объединяя множества двух ячеек. Если предпринята попытка выполнить вырезание в существующую часть лабиринта, то разрешить её, если ячейки находятся в разных множествах, и объединить ячейки, как это делается в алгоритме Краскала. Если рядом с текущей ячейкой нет несозданных «новых» ячеек, то перемещаем текущую ячейку в список «готовых». Лабиринт завершён, когда становится пустым список «активных». В конце выполняем объединение всех оставшихся множеств, как в алгоритме Краскала. Периодически можно создавать новые деревья, перемещая одну или несколько ячеек из списка «новых» в список «активных», как это делалось в начале. Управляя количество изначальных деревьев и долей новых создаваемых деревьев, можно сгенерировать множество уникальных текстур, сочетающихся с и так уже гибкими параметрами алгоритма выращивания дерева.
Алгоритм Эллера: это особый алгоритм, потому что он не только быстрее всех остальных, но и не имеет очевидной смещённости или недостатков; кроме того, при его создании память используется наиболее эффективно. Для него даже не требуется, чтобы в памяти находился весь лабиринт, он использует объём, пропорциональный размеру строки. Он создаёт лабиринт построчно, после завершения генерации строки алгоритм больше её не учитывает. Каждая ячейка в строке содержится во множестве; две ячейки принадлежат одному множеству, если между ними есть путь по уже созданному лабиринту. Эта информация позволяет вырезать проходы в текущей строке без создания петель или изолированных областей. На самом деле это довольно похоже на алгоритм Краскала, только здесь формируется по одной строке за раз, в то время как Краскал просматривает весь лабиринт. Создание строки состоит из двух частей: случайным образом соединяем соседние в пределах строки ячейки, т.е. вырезаем горизонтальные проходы, затем случайным образом соединяем ячейки между текущей и следующей строками, т.е. вырезаем вертикальные проходы. При вырезании горизонтальных проходов мы не соединяем ячейки, уже находящиеся в одном множестве (потому что иначе создастся петля), а при вырезании вертикальных проходов мы должны соединить ячейку, если она имеет единичный размер (потому что если её оставить, она создаст изолированную область). При вырезании горизонтальных проходов мы соединяем ячейки, если они находятся в одинаковом множестве (потому что теперь между ними есть путь), а при вырезании вертикальных проходов когда не соединяемся с ячейкой, помещаем её в отдельное множество (потому что теперь она отделена от остальной части лабиринта). Создание начинается с того, что перед соединением ячеек в первой строке каждая ячейка имеет собственное множество. Создание завершается после соединения ячеек в последней строке. Существует особое правило завершения: к моменту завершения каждая ячейка должна находиться в одинаковом множестве, чтобы избежать изолированных областей. (Последняя строка создаётся объединением каждой из пар соседних ячеек, ещё не находящихся в одном множестве.) Лучше всего реализовывать множество с помощью циклического двусвязного списка ячеек (который может быть просто массивом, привязывающим ячейки к парам ячеек с обеих сторон того же множества), позволяющего выполнять за постоянное время вставку, удаление и проверку нахождения соседних ячеек в одном множестве. Проблема этого алгоритма заключается в несбалансированности обработки разных краёв лабиринта; чтобы избежать пятен в текстурах нужно выполнять соединение и пропуск соединения ячеек в правильных пропорциях.
Рекурсивное деление (Recursive division): этот алгоритм чем-то похож на recursive backtracking, потому что в них обоих применяются стеки, только он работает не с проходами, а со стенами. Начинаем с создания случайной горизонтальной или вертикальной стены, пересекающей доступную область в случайной строке или столбце, и размещаем вдоль неё случайным образом пустые места. Затем рекурсивно повторяем процесс для двух подобластей, сгенерированных разделяющей стеной. Для наилучших результатов нужно добавить отклонение в выборе горизонтали или вертикали на основе пропорций области, например, область, ширина которой вдвое больше высоты, должна более часто делиться вертикальными стенами. Это самый быстрый алгоритм без отклонений в направлениях, и часто он может даже соперничать с лабиринтами на основе двоичных деревьев, потому что он создаёт одновременно несколько ячеек, хоть и имеет очевидный недостаток в виде длинных стен, пересекающих внутренности лабиринта. Этот алгоритм является разновидностью вложенных фрактальных лабиринтов, только вместо постоянного создания лабиринтов ячеек фиксированного размера с лабиринтами одного размера внутри каждой ячейки, он случайным образом делит заданную область на лабиринт случайного размера: 1×2 или 2×1. Рекурсивное деление нельзя использовать для вырезания проходов, потому что это приводит к созданию очевидного решения, которое или следует вдоль внешнего края, или иначе напрямую пересекает внутреннюю часть.
Лабиринты на основе двоичных деревьев: по сути, это самые простые и быстрые из возможных алгоритмов, однако создаваемые лабиринты имеют текстуру с очень высокой смещённостью. Для каждой ячейки мы вырезаем проход или вверх, или влево, но никогда не в обоих направлениях. В версии с добавлением стен для каждой вершины добавляется сегмент стены, ведущий вниз или вправо, но не в обоих направлениях. Каждая ячейка независима от всех других ячеек, потому что нам не нужно при её создании проверять состояние каких-то других ячеек. Следовательно, это настоящий алгоритм генерации лабиринтов без памяти, не ограниченный по размерам создаваемых лабиринтов. По сути, это двоичное дерево, если рассматривать верхний левый угол как корень, а каждый узел или ячейка имеет один уникальный родительский узел, являющийся ячейкой сверху или слева от неё. Лабиринты на основе двоичных деревьев отличаются от стандартных идеальных лабиринтов, потому что в них не может существовать больше половины типов ячеек. Например, в них никогда не будет перекрёстков, а все тупики имеют проходы, ведущие вверх или влево, и никогда не ведущие вниз или вправо. Лабиринты склонны иметь проходы, ведущие по диагонали из верхнего левого в нижний правый угол, и по ним гораздо проще двигаться из нижнего правого в верхний левый угол. Всегда можно перемещаться вверх или влево, но никогда одновременно в оба направления, поэтому всегда можно детерминированно перемещаться по диагонали вверх и влево, не сталкиваясь с барьерами. Иметь возможность выбора и попадать в тупики вы начнёте, перемещаясь вниз и вправо. Учтите, что если перевернуть лабиринт двоичного дерева вниз головой и считать проходы стенами, и наоборот, то результатом по сути будет другое двоичное дерево.
Лабиринты Sidewinder: этот простой алгоритм очень похож на алгоритм двоичного дерева, но немного более сложен. Лабиринт генерируется по одной строке за раз: для каждой ячейки случайным образом выбирается, нужно ли вырезать проход, ведущий вправо. Если проход не вырезан, то мы считаем, что только что завершили горизонтальный проход, образованный текущей ячейкой и всеми ячейками слева, вырезавшими проходы, ведущими в неё. Случайным образом выбираем одну ячейку вдоль этого прохода и вырезаем проход, ведущий из неё вверх (это должна быть текущая ячейка, если соседняя ячейка не вырезала проход). В то время как лабиринт двоичного дерева всегда поднимается вверх от самой левой ячейки горизонтального прохода, лабиринт sidewinder поднимается вверх от случайной ячейки. В двоичном дереве у лабиринта в верхнем и левом крае есть один длинный проход, а в лабиринте sidewinder есть только один длинный проход по верхнему краю. Как и лабиринт двоичного дерева, лабиринт sidewinder можно без ошибок и детерминированно решить снизу вверх, потому что в каждой строке всегда будет ровно один проход, ведущий вверх. Решение лабиринта sidewinder никогда не делает петель и не посещает одну строку больше одного раза, однако оно «извивается из стороны в сторону». Единственный тип ячеек, который не может существовать в лабиринте sidewinder — это тупик с ведущим вниз проходом, потому что это будет противоречить правилу, что каждый проход, ведущий вверх, возвращает нас к началу. Лабиринты sidewinder склонны к появлению элитного решения, при котором правильный путь оказывается очень прямым, но рядом с ним есть множество длинных ошибочных путей, ведущих сверху вниз.
В этой таблице вкратце представлены характеристики описанных выше алгоритмов создания идеальных лабиринтов. Для сравнения добавлен алгоритм одномаршрутного лабиринта (теоретически одномаршрутные лабиринты являются идеальными). Объяснение столбцов:
Существует множество способов решения лабиринтов, и каждый из них имеет собственные характеристики. Вот список конкретных алгоритмов:
Следование вдоль стен (Wall follower): это простой алгоритм решения лабиринтов. Приоритетом для него является проходящий лабиринт объект («вы»), он всегда очень быстр и не использует дополнительной памяти. Начинаем идти по проходам и при достижении развилки всегда поворачиваем направо (или всегда налево). Чтобы применить такое решение лабиринта в реальном мире, нужно положить руку на правую (или левую) стену и постоянно держать её на стене в процессе прохождения лабиринта. При желании можно помечать уже посещённые ячейки и ячейки, посещённые дважды. В конце можно вернуться назад по решению, следуя только по ячейкам, посещённым один раз. Этот метод необязательно найдёт кратчайшее решение, и он совершенно не работает, если цель находится в центре лабиринта и его окружает замкнутая цепь, потому что вы будете ходить вокруг центра и со временем придёте к началу. Следование вдоль стены в 3D-лабиринте можно реализовать детерминированным способом, спроецировав 3D-проходы на 2D-плоскость, т.е. притворившись, что ведущие вверх проходы на самом деле ведут на северо-запад, а ведущие вниз ведут на юго-восток, а затем применить обычные правила следования вдоль стен.
Алгоритм Пледжа: это модифицированная версия следования вдоль стены, способная перепрыгивать между «островами» для решения тех лабиринтов, которые не способно следование вдоль стен. Это гарантированный способ достижения выхода на внешнем крае любого 2D-лабиринта из любой точки внутри, однако он не способен выполнить обратную задачу, т.е. найти решение внутри лабиринта. Он отлично подходит для реализации с помощью сбегающего из лабиринта робота, потому что он сможет выбраться из любого лабиринта, не помечая и не запоминая ни каким образом путь. Начинаем с выбора направления и при возможности всегда движемся в этом направлении. Упёршись в стену, начинаем следовать вдоль неё, пока не сможем снова пойти в выбранном направлении. Стоит заметить, что следование вдоль стены нужно начинать с дальней стены, в которую мы упёрлись. Если в этом месте проход делает поворот, то это может привести к развороту посередине прохода и возврату тем же путём, которым мы пришли. При следовании вдоль стены считаем количество сделанных поворотов, например, поворот налево — это -1, а поворот направо — это 1. Прекращаем следование вдоль стен и начинаем двигаться в выбранном направлении только тогда, когда общая сумма сделанных поворотов равна, т.е. если вы повернулись на 360 градусов и более, то продолжаем следовать вдоль стены пока не «распутаемся». Подсчёт гарантирует, что рано или поздно мы достигнем дальней части «острова», в котором находимся в данный момент, и перепрыгнем на следующий остров в выбранном направлении, после чего продолжим прыгать между островами, пока не упрёмся в стену границы, после чего следование вдоль стен приведёт нас к выходу. Стоит учесть, что алгоритм Пледжа может заставить нас посетить проход или начальную точку несколько раз, однако в последующие разы вы всегда будете иметь другую сумму поворотов. Без разметки пути единственный способ узнать, что лабиринт нерешаем — постоянное увеличение суммы поворотов, хотя в решаемых лабиринтах со спиральным прохождением сумма поворотов тоже может достигать больших значений.
Алгоритм цепей: алгоритм цепей (Chain algorithm) решает лабиринт, воспринимая его как множество лабиринтов меньшего размера (подобно звеньям цепи) и решая их по порядку. Мы должны указать нужные места начала и конца, и алгоритм всегда найдёт путь от начала до конца, если он существует. При этом решение склонно быть разумно коротким, если даже не кратчайшим. Это означает, что таким способом нельзя решать лабиринты, в которых неизвестно точное расположение конца. Он наиболее похож на алгоритм Пледжа, потому что по сути это алгоритм следования вдоль стен со способом перепрыгивания между островами. Начинаем с рисования прямой линии (или хотя бы линии без самопересечений) от начала до конца, позволяя ей при необходимости пересекать стены. Затем просто следуем по линии от начала до конца. Если мы натыкаемся на стену, то не можем пройти через неё, а значит должны обходить. Отправляем двух следующих вдоль стен «роботов» по каждому из направлений вдоль стены, на которую наткнулись. Если робот снова пересечётся с указующей линией в той точке, где она ближе к выходу, тогда останавливаемся и следуем по этой стене, пока не доберёмся до неё сами. Продолжаем следовать по линии и повторять процесс, пока не достигнем конца. Если оба робота вернутся к их исходным локациям и направлениям, то дальнейшие точки вдоль прямой недостижимы и лабиринт нерешаем.
Recursive backtracker: этот алгоритм находит решение, но оно необязательно будет кратчайшим. Приритетом для него является проходящий лабиринт объект, он быстр для всех типов лабиринтов и использует стек размером вплоть до размера лабиринта. Он очень прост: если мы находимся возле стены (или в помеченной линией области), то возвращаем «неудача», иначе, если мы находимся в конце, возвращаем «успех», иначе, рекурсивно пробуем двигаться во всех четырёх направлениях. Рисуем линию, когда пытаемся пройти в новом направлении и удаляем её, если возвращено значение «неудача»; после достижения состояния «успех» у нас будет нанесено линиями единственное решение. При возврате назад (backtracking) лучше помечать пространство особым значением посещённых мест, чтобы мы не посещали их снова, приходя с другого направления. По сути, в программировании это называется поиском в глубину. Этот метод всегда находит решение, если оно существует, но оно необязательно будет самым коротким.
Алгоритм Тремо (Trémaux’s algorithm): этот метод решения лабиринтов разработан для использования человеком внутри лабиринта. Он похож на recursive backtracker и находит решение для всех лабиринтов: при движении по проходу мы рисуем линию за собой, помечающую наш путь. При попадании в тупик поворачиваемся назад и возвращаемся тем же путём, которым пришли. Дойдя до развилки, на которой ещё не были, случайным образом выбираем новый проход. Если мы проходим по новому проходу и доходим до развилки, которую посещали ранее, то считаем её тупиком и возвращаемся тем же путём, которым пришли. (Этот последний этап является самым важным, он не позволяет двигаться кругами и пропускать проходы в плетёном лабиринте.) Если двигаясь по проходу, который мы посещали раньше (т.е. раньше пометили), мы наткнулись на развилку, то выбираем любой новый проход, если это возможно, в противном случае выбираем старый проход (т.е. тот, который мы раньше пометили). Все проходы будут или пустыми, то есть мы их ещё не посещали, помеченными один раз,, то есть мы там были ровно один раз, или помеченными дважды, то есть мы двигались по ним и вынуждены были возвращаться в обратном направлении. Когда мы наконец достигнем решения, то помеченные один раз пути будут составлять прямой путь до самого начала. Если у лабиринта нет решения, то мы окажемся в начале, а все проходы будут помечены дважды.
Заполнитель тупиков (Dead end filler): это простой алгоритм решения лабиринтов. Приоритетом для него является лабиринт, он всегда очень быстр и не использует дополнительной памяти. Мы просто сканируем лабиринт и заполняем каждый тупик, заливая проход в обратном порядке от тупика, пока не достигнем развилки. В том числе это относится и к заливке проходов, которые стали частями тупиков после удаления других тупиков. В конце у нас останется одно решение, или несколько решений, если у лабиринта их больше одного. Алгоритм всегда находит для идеальных лабиринтов одно уникальное решение, но не особо преуспевает в лабиринтах с сильным плетением, и на самом деле почти бесполезен во всех лабиринтах без тупиков.
Cul-de-sac filler: этот метод находит и заполняет тупиковые развязки или петли, то есть конструкции в лабиринте, состоящие из тупикового пути с единственной петлёй в конце. Как и в dead end filler, приоритетом здесь является лабиринт, алгоритм всегда быстр и не использует дополнительной памяти. Сканируем лабиринт и для каждой петлевой развилки (петлевая развилка — это такая развилка, в которой два ведущих из неё прохода соединяются друг с другом, по пути не образуя новых развилок) добавляем стену, чтобы превратить всю петлю в длинный тупик. Затем мы запускаем dead end filler. В лабиринтах могут быть петли, выдающиеся из других конструкций, которые становятся петлями после удаления первых петель, поэтому весь процесс нужно повторять, пока при сканировании ничего не станет происходить. Этот алгоритм не очень полезен в сложных, сильно плетёных лабиринтах, но будет отсекать больше путей, чем простой dead end filler.
Blind alley filler: этот метод находит все возможные решения, вне зависимости от того, насколько они длинные или короткие. Он делает это, заполняя все тупиковые развязки. Тупиковая развязка — это такая конструкция, в которой двигаясь в одном направлении, для достижения цели придётся возвращаться назад по тому же пути в другом направлении. Все тупики являются тупиковыми развязками, как и все петли, описанные в алгоритме cul-de-sac filler, а также секции проходов любого размера. соединённые с остальной частью лабиринта единственным проходом. Приоритет он отдаёт лабиринту, не использует дополнительной памяти, но, к сожалению, довольно медленный. В каждой развилке мы отправляем следующего вдоль стен робота по каждому проходу, ведущему из неё, и смотрим, вернулся ли отправленный по пути робот тем же маршрутом (то есть не пришёл с другого направления и не вышел из лабиринта). Если это происходит, то такой проход и всё после него не может быть никаким путём решения, поэтому мы перекрываем этот проход и заливаем всё за ним. Этот алгоритм заполняет всё то же, что и cul-de-sac filler и кое-что ещё, однако описанный ниже алгоритм collision solver заполнит всё то же, что и этот алгоритм и кое-что ещё.
Blind alley sealer: этот алгоритм похож на blind alley filler тем, что он тоже находит все возможные решения, удаляя из лабиринта тупиковые развязки. Однако он заполняет только проходы в каждую тупиковую развязку и не касается набора проходов в их конце. В результате он создаст во всех тупиковых развязках и петлях сложнее простых тупиков недостижимые проходы. Этот алгоритм отдаёт приоритет лабиринту, работает гораздо быстрее, чем blind alley filler, хоть и требует дополнительной памяти. Мы определяем каждую соединённую секцию стен в уникальное множество. Чтобы сделать это, для каждой секции стен, ещё не находящихся в множестве, мы выполняем заливку поверх стен в этой точке, и определяем все достижимые стены в новое множество. После того, как все стены окажутся в множествах, мы проверяем каждую секцию проходов. Если стены по обеим её сторонам находятся в одном множестве, то мы перекрываем этот проход. Такой проход должен быть тупиковой развязкой, потому что стены по обеим сторонам соединены друг с другом, образуя огороженную площадку. Стоит заметить, что подобную технику можно использовать для помощи в решении гиперлабиринтов благодаря перекрытию пространства между ветвями, соединёнными друг с другом.
Поиск кратчайшего пути (Shortest path finder): как можно понять из названия, этот алгоритм находит кратчайшее решение, при наличии нескольких решений выбирая одно из них. Он множество раз отдаёт приоритет находящемуся в лабиринте, быстр для всех типов лабиринтов и требует довольно много дополнительной памяти, пропорциональной размеру лабиринта. Как и collision solver, он, по сути, заливает лабиринт «водой» так, что всё на одном расстоянии от начала заливается одновременно (в программировании это называется поиском в ширину), однако каждая «капля» или пиксель, запоминает, каким пикселем они были заполнены. Как только в решение попадает «капля», мы возвращаемся обратно от неё к началу, и это будет кратчайшим путём. Этот алгоритм хорошо работает для любых входных данных, потому что в отличие от большинства остальных не требует наличия в лабиринте каких-то проходов в пиксель шириной, по которым можно пройти. Стоит заметить, что это, по сути, алгоритм поиска пути A* без эвристики, то есть всему движению присваивается одинаковый вес.
Поиск кратчайших путей (Shortest paths finder): он очень похож на поиск кратчайшего пути, только находит все кратчайшие решения. Как и поиск кратчайшего пути, он множество раз отдаёт приоритет находящемуся в лабиринте, быстр для всех типов лабиринтов, требует дополнительной памяти, пропорциональной размеру лабиринта, и хорошо работает с любыми входными данными, потому что не требует, чтобы в лабиринте были какие-то проходы шириной в один пиксель, по которым можно пройти. Кроме того, как и поиск кратчайшего пути, он выполняет поиск в ширину, заполняя лабиринт «водой» так, что всё на одинаковом расстоянии от начала заполняется одновременно, только здесь каждый пиксель запоминает, как далеко он находится от начала. После достижения конца выполняется ещё один поиск в ширину, начинающийся с конца, однако в него включаются только те пиксели, чьё расстояние на одну единицу меньше, чем у текущего пикселя. Включённые в путь пиксели точно помечают все кратчайшие пути, так как в тупиковых развязках и в не самых коротких путях расстояния в пикселях будут скакать или увеличиваться.
В этой таблице вкратце перечислены характеристики описанных выше алгоритмов решения лабиринтов. По этим критериям можно классифицировать и оценивать алгоритмы решения лабиринтов. Объяснения столбцов:
Кроме создания и решения лабиринтов, с ними можно выполнять другие операции:
Как при помощи программы на языке Pascal научить компьютер искать выход из лабиринта?
Кратчайшие пути в невзвешенных графах
Кратчайшие пути в невзвешенных графах 1 Постановка задачи Дан простой связный неориентированный граф и задана стартовая вершина s. Необходимо найти кратчайшее расстояние из этой вершины до всех остальных.
Подробнее
Однопроходные алгоритмы
Однопроходные алгоритмы (для тех, кто предпочитает Java, рекомендуем курс «Алгоритмы. Олимпиадное программирование» фирмы «1С», см. http://club.1c.ru) Часто бывает нужно обработать какую-нибудь длинную
Подробнее
ДЕТЕРМИНИРОВАННАЯ РАСКРАСКА ГРАФОВ
Секция 7. Технологии и системы искусственного интеллекта 433 УДК 004.932.2+004.932.72’1 Е.С. Левицкая Донецкий национальный технический университет, г. Донецк Кафедра программного обеспечения интеллектуальных
Подробнее
Лабораторная работа 7
Лабораторная работа Тема: «Метод Форда» Цель работы: Получить практические навыки решения сетевых задач методом Форда. Предварительная подготовка: спец. дисциплина «Математические методы» Количество часов:
Подробнее
Кнопка регистрации в elibrary.ru
Российский индекс научного цитирования (РИНЦ) (www.elibrary.ru) и аналитическая система Science Index для авторов. Управление личным профилем, определение наукометрических индексов учѐного Вера Хорина
Подробнее
Разбор задачи «Урок физкультуры»
Разбор задачи «Урок физкультуры» Первое замечание, существенно упрощающее понимание решение данной задачи, состоит в том, что нас интересует только соотношение сил остальных учеников с силой Коли, но не
Подробнее
Методы поиска в пространстве состояний.
Методы поиска в пространстве состояний. Лекция 3. Специальность : 220400 Определение 3. Решающую последовательность образуют операторы, которые связаны с дугами пути от целевой вершины к начальной. Поиск
Подробнее
ПОИСК В ГЛУБИНУ И В ШИРИНУ
ПОИСК В ГЛУБИНУ И В ШИРИНУ Определив направление поиска (от данных или от цели), алгоритм поиска должен определить порядок исследования состояний дерева или графа. В этом разделе рассматриваются два возможных
Подробнее
ФОРМА оформления решений заданий заочного тура (Интернет-олимпиады) по информатике Решения задач по информатике высылаются на почтовый ящик [email protected] На данный ящик в архиве (одним файлом)
Подробнее
B5 (повышенный уровень, время 10 мин)
B5 (повышенный уровень, время 0 мин) Тема: Поиск алгоритма минимальной длины для исполнителя. Что нужно знать: каких-либо особых знаний из курса информатики не требуется, задача решаема на уровне 6-7 класса
Подробнее
РАЗДЕЛ I. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
РАЗДЕЛ I. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Направленность техническая Профиль IT-технологии Вид деятельности Решение математических задач. Программирование. Программа по форме организации — групповая Срок реализации
Подробнее
ТЕОРИЯ. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ — 2. Нумерация разделов по ЕГЭ-2013 АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ. А5, А12, A13, В2, B3, В6, В7, В14
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГИМНАЗИЯ ПРИМОРСКОГО РАЙОНА САНКТ-ПЕТЕРБУРГА ТЕОРИЯ. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ — АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ. А, А, A, В, B, В, В7, В Нумерация
Подробнее
Кочетов Юрий Андреевич. Лекция 1
Дискретная математика Часть 2 Кочетов Юрий Андреевич http://www.math.nsc.ru/lbrt/k5/dm.html Лекция 1 Алгоритмы, сортировки, AVL деревья 1 Алгоритмы и их сложность Компьютеры выполняют (пока) лишь корректно
Подробнее
ВВЕДЕНИЕ В БИОИНФОРМАТИКУ
ВВЕДЕНИЕ В БИОИНФОРМАТИКУ Лекция 6 Элементы теории графов Новоселецкий Валерий Николаевич к.ф.-м.н., доц. каф. биоинженерии [email protected] Сайт курса http://intbio.org/bioinf2018 2 Задача
Подробнее
ДИСКРЕТНЫЕ ФУНКЦИИ И АВТОМАТЫ
ВЕСТНИК ТОМСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА 2011 Управление, вычислительная техника и информатика 3(16) ДИСКРЕТНЫЕ ФУНКЦИИ И АВТОМАТЫ УДК 519.7 А.Д. Закревский АЛГОРИТМ МАТРИЧНОГО ОТОБРАЖЕНИЯ ГРАФА
Подробнее
Задача A. Фальшивые монеты
ЛКШ.017.Июль.A0.Kotlin Challenge Задача A. Фальшивые монеты секунды В королевстве Байтландия завелись гоблины-фальшивомонетчики, выпускаемые ими монеты исчезают на следующее утро. По дороге домой гном
Подробнее
Информатика, муниципальный этап
Департамент образования Ярославской области Всероссийская олимпиада школьников 2015/2016 учебного года Информатика, муниципальный этап Теоретический тур. Решения и указания по проверке. Оценка работы производится
Подробнее
Нижние оценки Гилмора и Гомори
Нижние оценки Гилмора и Гомори Имеется неограниченное число контейнеров единичной вместимости. Для каждой заготовки i L задана длина 0 < w i < 1 и их количество n i 1. Требуется упаковать заготовки в минимальное
Подробнее
Нахождение путей в графе
Нахождение путей в графе В основе построения большинства алгоритмов на графах лежит систематический перебор вершин графа, при котором каждая вершина просматривается в точности один раз, а количество просмотров
Подробнее
Алгоритмы и структуры данных
Алгоритмы и структуры данных Лекция 7. Графы (поиск кратчайшего пути). (с) Глухих Михаил Игоревич, [email protected] 2 Граф Граф = вершины (узлы) + рёбра (дуги) Вершины и рёбра могут иметь свойства 3 Применение
Подробнее
Приложение «Школьный портал»
Система «Школьный портал» Московской области «Школьный портал» Московской области Приложение «Школьный портал» Руководство педагога Версия 1.0 Оглавление ОГЛАВЛЕНИЕ… 2 1. ПОДГОТОВКА К РАБОТЕ С ПРИЛОЖЕНИЕМ…
Подробнее
Поиск в ширину, поиск в глубину
Поиск в ширину, поиск в глубину Рассмотрим алгоритмы для решения различных задач на графах. Сначала речь пойдет о задачах анализа графов с целью выявления их структуры и вычисления метрических характеристик.
Подробнее
Поиск в глубину, алгоритм лабиринта | Мигель Кано
Что такое поиск в глубину?
Поиск в глубину — это алгоритм, который можно использовать для создания лабиринта. Идея действительно проста и легко реализуется с помощью рекурсивного метода или стека.
Обычно вы начинаете со случайной точки и продолжаете копать пути в одном из 4 направлений (вверх, вправо, вниз, влево) до тех пор, пока не перестанете двигаться дальше. Как только вы застряли, вы делаете шаг назад, пока не найдете открытый путь. Вы бы продолжили копать оттуда.Это просто повторение всего этого.
Прежде всего, я хотел бы немного глубже объяснить общую идею, которую вы можете применить, используя выбранный вами язык программирования. После того, как вы представите себе картину, вы можете взглянуть на пример кода и апплет в java.
Пояснение
Создайте двумерный массив int с нечетным размером строки и столбца. 0 представляет собой пути (оранжевая ячейка), а 1 — стены (черная ячейка).
Установить все ячейки на 1 (стена).Сейчас нет путей.
Теперь давайте установим отправную точку. Сгенерируйте нечетные числа для строки и столбца. Установите для этой ячейки значение 0. Используйте переменные row и col для отслеживания текущего местоположения. На картинке выше это будет row = 3, col = 5. Для ясности я заполню текущую ячейку красным цветом.
Теперь выберите случайное направление (вверх, вправо, вниз или влево), в котором вы движетесь. Вы всегда будете двигаться на 2 клетки. На картинке выше показано, как текущая ячейка движется вниз.Есть несколько вещей, которые вам нужно проверить при переезде. Во-первых, вам нужно проверить, находятся ли 2 клетки впереди этого направления за пределами лабиринта. Затем вы проверяете, являются ли 2 клетки впереди путем (0) или стеной (1). Если это стена, вы можете перемещаться, установив для этих двух ячеек значение 0 (путь). Обновите свое текущее местоположение, которое сейчас row = 5, col = 5.
Продолжая копать, как указано выше, вы замечаете, что зашли в тупик. В этом случае продолжайте перемещать текущую ячейку к предыдущим ячейкам, пока не сможете перейти в новом направлении.Это называется возвратом. Текущее местоположение находится в row = 7, col = 7, поэтому вы вернетесь к row = 7, col = 5 на картинке выше. Вы можете реализовать эту логику, используя рекурсивный метод или стек.
Итак, продолжайте копать, как показано на рисунке. Для большей наглядности я менял цвет стрелки каждый раз, когда она заходит в тупик.
Наконец, это окончательный результат. Естественно, что лабиринт такого размера становится слишком простым. Чем больше лабиринт, тем сложнее он будет.
Пример апплета
Использование рекурсивного метода
После выбора начальной точки передайте эту информацию рекурсивному методу. В рекурсивном методе вы можете сделать следующее…
- Сгенерировать массив int с 4 случайными числами для представления направлений.
- Запустить цикл for 4 раза.
- Настройте оператор switch, чтобы заботиться о 4 направлениях.
- Для этого направления проверьте, будет ли новая ячейка вне лабиринта или это уже открытый путь.Если да, ничего не делайте.
- Если ячейка в этом направлении является стеной, установите для этой ячейки путь и вызовите рекурсивный метод, передавая новую текущую строку и столбец.
- Готово.
Пример кода
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 год 22 23 24 25 26 год 27 28 год 29 30 31 год 32 33 34 35 год 36 37 38 39 40 41 год 42 43 год 44 год 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 год 82 83 84 85 86 87 88 89 90 91 92 | public int [] [] generateMaze () {
int [] [] лабиринт = новый int [высота] [ширина];
// Инициализируем
для (int я = 0; я <высота; я ++)
для (int j = 0; j |
Поиск в глубину (DFS) | Блестящая вики по математике и науке
Ниже приведены примеры псевдокода и кода Python, реализующие DFS как рекурсивно, так и нерекурсивно. Этот алгоритм обычно использует стек для отслеживания посещенных узлов, поскольку последний замеченный узел является следующим, который будет посещен, а остальные сохраняются для последующего посещения.
Псевдокод [1]
Инициализировать пустой стек для хранения узлов, S.Для каждой вершины u определим u.visited как ложное. Вставьте корень (первый узел, который нужно посетить) на S. Пока S не пуст: Вставьте первый элемент в S, u. Если u.visited = false, то: U.visited = true для каждого непосещенного соседа w из u: Вставьте w в S. Завершить процесс, когда все узлы будут посещены.Реализация Python без рекурсии
def depth_first_search (график): посетили, stack = set (), [root] в то время как стек: вершина = стек.поп () если вершина не в посещенной: visit.add (вершина) stack.extend (граф [вершина] - посещено) вернуться посетил
DFS также может быть реализован с использованием рекурсии, что значительно сокращает количество строк кода.
Реализация Python с использованием рекурсии
def depth_first_search_recursive (график, начало, посещение = Нет): при посещении - Нет: посетил = set () посетил.добавить (начало) для следующего в графе [начало] - посетил: depth_first_search_recursive (график, следующий, посещенный) вернуться посетил
Обычно алгоритм изменяют, чтобы отслеживать ребра, а не вершины, поскольку каждое ребро описывает узлы на каждом конце. Это полезно, когда кто-то пытается восстановить пройденное дерево после обработки каждого узла. В случае леса или группы деревьев этот алгоритм можно расширить, включив в него внешний цикл, который выполняет итерацию по всем деревьям для обработки каждого отдельного узла.
Существует три различных стратегии реализации DFS: для предварительного заказа , для заказа и для последующего заказа .
Предварительный заказ DFS работает, посещая текущий узел и последовательно перемещаясь влево, пока не будет достигнут лист, посещая каждый узел по пути к нему. Когда слева от узла больше нет дочерних элементов, обращаются к дочерним элементам справа. Это самый стандартный алгоритм DFS.
Вместо посещения каждого узла по мере его прохождения вниз по дереву алгоритм по порядку находит крайний левый узел в дереве, посещает этот узел, а затем посещает родительский узел этого узла.Затем он переходит к дочернему элементу справа и находит следующий крайний левый узел в дереве для посещения.
Стратегия после заказа работает, посещая крайний левый лист в дереве, затем поднимаясь до родительского и опускаясь вниз по второму крайнему левому листу в той же ветви, и так далее, пока родительский узел не станет последним узлом, который нужно посетить в пределах ветка. Этот тип алгоритма отдает приоритет обработке листьев перед корнями в случае, если цель находится в конце дерева.
алгоритмов поиска в лабиринте
Поиск - это алгоритм, который проходит по графу в
поиск одного или нескольких целевых узлов.Как мы узнаем через несколько недель, лабиринт - это
специальный экземпляр математического объекта, известного как «график». В
а пока мы будем использовать «лабиринт» и «график».
взаимозаменяемо. Мы рассмотрим три стратегии обхода графа для
быстро найти пончики в лабиринте. Основная идея всех трех одинаковых:
все они посещают узел, который является «следующим» в структуре данных, которую они
поддерживать (стек, очередь или приоритетная очередь (реализованная как двоичная куча
или три кучи)), отметьте его, а затем добавьте его непосещенных соседей в структуру данных.Обходы различаются тем, какие узлы они исследуют первыми, а какие оставляют.
Для последующего.
Основной алгоритм, используемый во всех трех поисках, следующий. Тип Set реализуется одним из трех ADT и влияет на порядок, в котором исследуются узлы.
Поиск (Лабиринт м )
Отметка м .Начальный узел "Посещение в процессе"
Набор. Вставка ( м . Начальный узел)
Пока установлен.NotEmpty
c <- Set.Remove
Если c является целью
Exit
Else
Foreach сосед n of c
If n "Unvisited"
Mark n «Посещение в процессе»
Set.Insert ( n )
Mark c «Visited»
Завершение процедуры
Этот алгоритм использует три состояния для каждой ячейки.
- Не посещал : Ячейка
еще не посетил поиск.
- Идет визит :
Ячейка была обнаружена, но поиск не оценил ее
в набор следует добавить соседей.
- Посещено : ячейка
был посещен, и все его соседи добавлены / добавлены в набор (т. е. они уже находятся в статусе «Идет посещение» или «Посещены»).
Определяющей характеристикой этого поиска является
что всякий раз, когда DFS посещает ячейку лабиринта c , он затем ищет суб-лабиринт
чье начало c , прежде чем искать любую другую часть лабиринта.Это
достигается за счет использования стека для хранения узлов. Set.Insert
соответствует Push, а Set.Remove
к поп-музыке.
Конечным результатом является то, что DFS будет следовать некоторым
путь через лабиринт до упора, до тупика или ранее
посещенное место найдено. Когда это происходит, поиск возвращается назад, чтобы попытаться
другой путь, пока не найдет выход.
См. Эту страницу для получения дополнительной информации о DFS и BFS и эту страницу для графического сравнения BFS и DFS.
Определяющей характеристикой этого поиска является
что всякий раз, когда BFS исследует ячейку лабиринта c , он добавляет соседей c
к набору ячеек, которые он будет исследовать позже.В отличие от DFS, эти
ячейки удаляются из этого набора в порядке их посещения; который
есть, BFS поддерживает очередь ячеек, которые были посещены, но еще не
обследован (осмотр камеры c заключается в посещении всех ее
соседи). BFS реализован с использованием очереди для набора. Set.Insert
соответствует enQueue, а Set.Remove
в deQueue.
Конечным результатом является то, что BFS посетит все
клетки в порядке их удаленности от входа.Сначала он посещает все
места на расстоянии одного шага, затем он посещает все места
которые находятся на расстоянии двух шагов, и так далее, пока не будет найден выход. Из-за этого,
У BFS есть приятное свойство: он естественным образом обнаруживает кратчайший маршрут.
через лабиринт.
См. Это
страницу для получения дополнительной информации о DFS и BFS, и это
страница для графического сравнения BFS и DFS.
III. Лучший первый поиск
Определяющая характеристика этого
поиск таков, в отличие от DFS или BFS
(который слепо исследует / расширяет ячейку, ничего не зная о ней или ее
properties), лучший первый поиск использует функцию оценки (иногда называемую
"эвристический"), чтобы определить, какой объект является наиболее перспективным, и
затем исследует этот объект.Реализовано такое поведение «сначала лучший».
с PriorityQueue
для набора. Set.Insert
соответствует Insert, а Set.Remove
в DeleteMin.
Для наших бегунов по лабиринту объекты, которые мы будем хранить в PriorityQueue, являются ячейками лабиринта, а наша эвристика будет
сотовый "Манхэттен"
расстояние »от выхода. Манхэттен
расстояние - это быстро вычисляемое и удивительно точное измерение того, как
скорее всего, на пути к выходу будет MazeCell.
Геометрически расстояние Манхэттена равно
расстояние между двумя точками, если вам разрешалось ходить только по тропинкам, которые были
под углом 90 градусов друг к другу (аналогично прогулке по улицам Манхэттена).Математически Манхэттен
расстояние:
| ячейка x
- выход x | + | ячейка y
- выход y |
(Иногда Манхэттен
расстояние увеличивается на постоянный коэффициент, чтобы обеспечить уникальные значения для каждого
ячейка)
Конечным результатом является то, что при первом поиске лучше всего будет посещаться то, что, по его мнению, является
сначала самые многообещающие ячейки, что дает лучшие первые некоторые из хороших свойств
как BFS, так и DFS. Однако это оставляет
лучший первый поиск, уязвимый для плохой эвристики или определенных типов лабиринтов, которые
использовать слабые места определенных эвристик.
См. Это
страницу для получения дополнительной информации о различных эвристиках (они будут использовать теорию игр
терминология).
Алгоритм создания лабиринта - поиск в глубину
Статьи -> Алгоритм создания лабиринта - поиск в глубину
Существует несколько алгоритмов генерации лабиринтов, которые можно использовать для случайной генерации n-мерных лабиринтов. В этом руководстве я обсуждаю один конкретный алгоритм создания лабиринта, который рассматривает завершенный лабиринт как дерево, ветви которого представляют пути через лабиринт.Для создания дерева используется случайный поиск в глубину - алгоритм, который строит дерево случайным образом, пока дерево или лабиринт не будет завершено. Чтобы понять этот тип алгоритма создания лабиринта более подробно, это помогает понять, как лабиринт представлен в виде дерева, а затем как алгоритм обхода может быть использован для создания лабиринта.
В двух измерениях лабиринт представляет собой серию путей, разделенных стенами, и для упрощения создания можно представить лабиринт как двухмерную сетку.Сетка имеет ширину и высоту, и каждая позиция x / y в сетке может быть представлена в виде ячейки. При таком рассмотрении сетка может рассматриваться как граф G , в котором каждая ячейка является узлом, соединенным с каждым из своих четырех соседей стеной (исключение из этого правила - для краевых и угловых ячеек, которые имеют 3 и 2 соседа соответственно). Затем алгоритм находит на основе случайного начального числа остовное дерево - или дерево, состоящее из всех вершин, но только некоторых из ребер - этого графа G .Алгоритм делает это следующим образом:
- Случайным образом выбрать узел (или ячейку) N .
- Поместите узел N в очередь Q .
- Пометить ячейку N как посещенную.
- Произвольно выбрать соседнюю ячейку A узла N , который не был посещен. Если были посещены все соседи N :
- Продолжать выталкивать элементы из очереди Q до тех пор, пока узел не встретится хотя бы с одним непосещенным соседом - назначьте этот узел N и перейдите к шагу 4.
- Если узлов нет: остановить.
- Разорвите стену между N и A .
- Присвойте значение A N .
- Перейти к шагу 2.
Граф и результирующее дерево можно легче визуализировать, запустив алгоритм на небольшой сетке ячеек 5x5, как показано на изображениях и видео ниже. A ) Исходный граф G , где каждая ячейка - или узел - (изображенный синим кружком) соединен со своими соседями ребром (обозначенным черной линией). B ) Результирующее дерево, в котором начальный узел изображен зеленым, а ветви - красным. C ) Ветви дерева представляют собой пути через сетку, таким образом, стены между каждой ячейкой (узлом) в дереве удаляются, когда две соседние ячейки соединяются ребром внутри дерева, что приводит к окончательному лабиринту. Пошаговый процесс создания этого лабиринта показан на видео ниже.
(А) | (В) |
(К)
(A) 2D-сетка, представленная в виде графика, (B) результирующее случайное разреженное дерево, полученное в результате выполнения алгоритма, описанного выше (C) результирующий лабиринт после алгоритма создания лабиринта (зеленый представляет начало - или корень - узел).
Пошаговое создание дерева выше. Зеленый цвет представляет начальный узел, красный - конечный узел (см. Ниже), а синий - текущий узел.
Вышеупомянутый алгоритм гарантирует путь между узлами результирующего связующего дерева, таким образом, можно сгенерировать начальную и конечную точки, так что лабиринт - от начала до конца - может быть решен. Метод определения начальной и конечной точек состоит в том, чтобы ограничить начальный случайный выбор на шаге (1) краевой ячейкой - ячейкой по краям сетки.Чтобы вычислить конец, можно пометить каждую граничную ячейку по мере их последующего обнаружения - размер очереди Q на этом этапе является показателем как расстояния, так и сложности. Таким образом, выбор наиболее удаленной ячейки может, по-видимому, создать самый сложный лабиринт (иногда это может быть не всегда, поскольку визуальные шаблоны и баланс дерева также могут играть роль в сложности).
Хотя приведенное выше является упрощенным представлением алгоритма, лабиринт можно сделать более сложным путем одного или нескольких изменений его структуры, например увеличения его размера, преобразования координат лабиринта, добавления дополнительных измерений или визуализации лабиринта в 3D.
Лабиринт с сеткой 100x100. Оба входа и выхода справа.
Овальный лабиринт. Была построена сетка 40x40, каждая стена (линия) преобразована из координатной сетки в сферические координаты. См. Раздел «Сопоставление квадрата с кругом»
.
К этой статье нет комментариев.
Вернуться к статьям
Лабиринтных алгоритмов
В предыдущей статье я писал
о решениях и алгоритмах миссии «Открытый лабиринт» в блоге CheckiO.С тех пор я получил много запросов, чтобы узнать немного больше о схемах и дать более интерактивное объяснение.
Итак, я собрал эту более подробную статью с некоторыми объяснениями алгоритма визуального лабиринта.
Вы можете увидеть, как BFS, DFS или A * ставят в очередь или стек и как они находят путь для
разные лабиринты.
Все примеры здесь основаны на оригинальном
«Открытый лабиринт»
миссия.В этой миссии вам дается карта лабиринта.
и ваша задача найти путь из одного угла в другой.
Лабиринт можно представить в виде графа, где пустые ячейки являются узлами, а соседние ячейки соединены.
Поскольку нам не нужно находить кратчайший путь, мы можем использовать различные алгоритмы обхода графа.
Сначала я хотел бы изменить представление лабиринта.В этой части нет необходимости, и мы можем обнаруживать «соседей», пока ищем путь.
Но новичкам будет проще разложить задачу и сначала сконвертировать
лабиринт в 2D-массив и в граф как словарь.
Наш график будет представлен в виде словаря, где ключи - координаты узлов,
значения - координаты соседнего узла, а направления - как к нему добраться.
Координаты узлов представлены в виде кортежа с двумя числами.Таким образом, каждая ячейка имеет уникальное имя.
Маршруты будут полезны для написания маршрута, когда мы ищем путь внутри лабиринта.
Сначала мы собираем все пустые ячейки и записываем их как ключи.
Затем соберите информацию о соседях. Мы могли бы сделать это за одну итерацию через
матрица с defaultdict, но я хочу попробовать более простой метод, лучше подходящий для новичков в Python.
Для каждой ячейки мы смотрим только на «южных» и «восточных» соседей и добавляем их как «связи».И этими направлениями мы добавляем обратное соединение «N» и «W» для соседних ячеек.
Таким образом мы пропускаем повторяющиеся операции.
Не забудьте проверить крайние случаи.
Ниже вы можете увидеть простой код для этого.
def maze2graph (лабиринт):
высота = длина (лабиринт)
width = len (лабиринт [0]), если высота иначе 0
graph = {(i, j): [] для j в диапазоне (ширина) для i в диапазоне (высота), если не лабиринт [i] [j]}
для строки, столбец в графике.ключи ():
если строка
В этих анимациях вы можете увидеть, как функция недавних проверок проверяет соседей.
Но в реализации Python это немного сложно, потому что словари py неупорядочены.
Эта анимация должна показать вам, как лабиринт принимает форму «скелета».
Поиск в ширину (BFS) - это алгоритм обхода или поиска пути в графе.Он начинается с некоторого произвольного узла графа и сначала исследует соседние узлы,
перед переходом к соседям следующего уровня. Для BFS мы используем очередь для хранения узлов, которые
буду изучать. Таким образом, мы сначала проверяем ближайшие узлы.
Это должно выглядеть так, как будто мы идем уровень за уровнем, и прежде чем мы перейдем к следующему уровню, мы должны
проверить все узлы на текущем уровне. Для поиска по графу очень важно записать все посещенные
узлов, или мы можем попасть в цикл.
BFS оптимален и гарантированно найдет лучшее из существующих решений.
Временная сложность для BFS (наихудший случай) составляет O (| V | + | E |), где | V | количество узлов и
| E | - количество ребер в графе.
В Python мы можем использовать deque как очередь или даже простой список (но это медленнее).
Ставим начальный узел в очередь.
Затем повторяйте эту процедуру до тех пор, пока не посетите целевой узел или
посетить все доступные узлы: взять первый из очереди, проверить, посещался он или нет,
проверьте, является ли это целью, поместите всех соседей в конец очереди, повторите.Для каждого шага мы отслеживаем не только узлы, но и направления, а также путь для текущего узла.
из коллекции import deque
def find_path_bfs (лабиринт):
начало, цель = (1, 1), (len (лабиринт) - 2, len (лабиринт [0]) - 2)
queue = deque ([("", начало)])
посетил = set ()
graph = maze2graph (лабиринт)
пока очередь:
путь, текущий = queue.popleft ()
если текущая == цель:
Обратный путь
если текущий в посещенном:
Продолжать
посетил.добавить (текущий)
для направления, сосед в графе [текущий]:
queue.append ((путь + направление, сосед))
вернуть "НЕТ ПУТЬ!" На следующей анимации вы можете увидеть, как BFS проходят через лабиринт.
Пронумерованные ячейки - это узлы в очереди (берем с наименьшим номером).
Посещаются серые клетки. Оранжевые клетки показывают получившийся маршрут.
Поиск в глубину (DFS) - это алгоритм, аналогичный BFS.Он начинается с некоторого произвольного узла графа, такого как BFS,
но исследует, насколько это возможно, каждую ветку.
Для нерекурсивной реализации DFS мы используем стек вместо очереди для хранения узлов.
который будет изучать. Таким образом, мы сначала проверяем те узлы, которые были добавлены в стек последними.
DFS не оптимален, и не гарантируется, что вы найдете лучшее решение.
Это означает, что DFS не лучший выбор для поиска пути в лабиринте, но у него есть другие приложения в
поиск связанных компонентов или создание лабиринта.
Код Python для DFS имеет лишь пару отличий от BFS.
Мы переименовали «очередь» в «стек» для удобства чтения, а «popleft ()» - в «pop ()».
из коллекции import deque
def find_path_dfs (лабиринт):
начало, цель = (1, 1), (len (лабиринт) - 2, len (лабиринт [0]) - 2)
stack = deque ([("", начало)])
посетил = set ()
graph = maze2graph (лабиринт)
в то время как стек:
путь, текущий = стек.поп ()
если текущая == цель:
Обратный путь
если текущий в посещенном:
Продолжать
visit.add (текущий)
для направления, сосед в графе [текущий]:
stack.append ((путь + направление, сосед))
вернуть "НЕТ ПУТЬ!" На следующей анимации вы можете увидеть, как DFS проходит через лабиринт.
Как мы видим, для пустой ячейки DFS работает хорошо, но не для «Snake and Short».Пронумерованные ячейки - это узлы в очереди (берем с наибольшим номером).
Посещаются серые клетки. Оранжевые клетки показывают получившийся маршрут.
A * - широко используемый алгоритм поиска пути и расширение алгоритма Эдсгера Дейкстры 1959 года.
A * использует жадный поиск и находит путь с наименьшими затратами
от заданного начального узла к одному целевому узлу из одной или нескольких возможностей.Когда A * пересекает график, он следует по пути с наименьшей ожидаемой общей стоимостью или расстоянием,
ведение сортированной очереди по приоритету из альтернативных сегментов пути по пути.
Он использует эвристическую функцию стоимости узла, чтобы определить порядок, в котором
поиск посещает узлы на графике.
В качестве A * мы берем первый узел, который имеет наименьшую суммарную стоимость пути и ожидаемую оставшуюся стоимость.
Но эвристика должна быть допустимой, то есть не должна переоценивать расстояние до цели.Временная сложность A * зависит от эвристики.
Для Python мы можем использовать модуль "heapq" для приоритетной очереди и
добавьте стоимостную часть каждого элемента.
Для лабиринта одной из самых простых эвристик может быть «Манхэттенское расстояние».
из heapq import heappop, heappush
def эвристика (ячейка, цель):
вернуть абс (ячейка [0] - цель [0]) + абс (ячейка [1] - цель [1])
def find_path_astar (лабиринт):
начало, цель = (1, 1), (len (лабиринт) - 2, len (лабиринт [0]) - 2)
pr_queue = []
heappush (pr_queue, (0 + эвристика (начало, цель), 0, "", начало))
посетил = set ()
graph = maze2graph (лабиринт)
в то время как pr_queue:
_, стоимость, путь, текущий = heappop (pr_queue)
если текущая == цель:
Обратный путь
если текущий в посещенном:
Продолжать
посетил.добавить (текущий)
для направления, сосед в графе [текущий]:
heappush (pr_queue, (стоимость + эвристика (сосед, цель), стоимость + 1,
путь + направление, сосед))
вернуть "НЕТ ПУТЬ!" На этой анимации вы можете увидеть, как A \ * проходит через лабиринт.
Как видим, этот алгоритм находит кратчайший путь и использует меньше ячеек, чем BFS.
Пронумерованные ячейки - это узлы в очереди приоритетов (по мере их добавления, но не по мере их использования).Посещаются серые клетки. Оранжевые клетки показывают получившийся маршрут.
Вот список книг, которые могут быть полезны для изучения Python, алгоритмов и искусственного интеллекта для GameDev:
Это партнерские ссылки Amazon, поэтому, если вы решите купить что-то из этих книг, автор этой страницы будет благодарен.
Четкое понимание алгоритма поиска в глубину и его реализации на Python: алгоритм графа | Рашида Насрин Саки
Учитесь с помощью Clear Visuals.Также узнайте о распространенной ошибке, которую люди допускают в алгоритме поиска в глубину
Что такое поиск в глубину?
Это один из широко используемых и очень популярных алгоритмов поиска по графу. Чтобы понять этот алгоритм, представьте себе лабиринт. Что нам делать, когда нужно решить лабиринт? Мы идем по маршруту, продолжаем идти, пока не найдем тупик. Зайдя в тупик, мы возвращаемся и продолжаем идти, пока не увидим путь, который не пробовали раньше. Выбери этот новый маршрут. Снова продолжаем идти, пока не найдем тупик.Вернитесь снова….
Поиск в глубину работает почти так же. Использование этого типа процесса поиска с возвратом. С начальной точки он движется до тех пор, пока не найдет больше путей, по которым следует идти. Затем возвращается в точку, где есть неизведанные пути. Он продолжает делать это до тех пор, пока не закончит перемещение всех узлов и ребер.
Это был самый простой способ ввести поиск в глубину. Я объясню это более подробно позже.
Почему важен поиск по глубине и ферту
Поиск в глубину имеет широкий спектр вариантов использования.
- Решение лабиринта или головоломки, как я описал выше
- Планирование проблемы
- Обнаружение цикла на графике
- Сетевой анализ
- Отображение маршрутов
- Топологическая сортировка
И многое другое. Поиск в глубину также является основой для многих других сложных алгоритмов.
Как работает поиск в глубину?
В этом разделе мы визуально увидим рабочий процесс поиска в глубину.Вот график, и исходный узел показан как узел u.
Мы можем перейти к узлу v или x из u. Мы можем пойти в любом направлении. Я выбираю перейти к v. Из графика видно, что существует только один исходящий маршрут от v. Это y.
Из графика видно, что существует только один исходящий маршрут из v. Это y. Итак, мы находимся сейчас в у.
Как и раньше, от y также был один исходящий путь. Это было до x. Итак, нам нужно было прийти к x. Это единственный выбор.
Смотрите, мы застряли! Исходящего пути от x нет.Как уже говорилось ранее, в этой ситуации мы возвращаемся назад.
Вернувшись назад, мы вернулись к у.
Отсюда нет дорог. Итак, вернемся снова.
Теперь мы в v. Исследуем v. Но исходящего пути из v снова нет. Так что вернитесь еще на один шаг.
Мы вернулись к еще одному шагу, и это наш исходный узел u.
Здесь мы видим, что существует неисследованный нами исходящий путь.
Переходим от u к x и видим, что x уже посещался раньше. Этот тип кромки называется передней кромкой. Тогда от x также есть путь к v. Узел v также посещается, и v является предком x. Итак, этот путь называется задней кромкой.
Мы закончили со всеми узлами и ребрами в круге uvyx. Здесь мы исследуем новый узел w.
Из w мы можем перейти к z или y. Я предпочитаю сейчас пойти в z.
Обратите внимание, z возвращается к z, используя задний край .
Некуда идти от з. Итак, мы снова возвращаемся назад и возвращаемся к w.И у w есть одно неисследованное ребро, идущее к y.
Этот тип соединительных кромок называется поперечной кромкой.
Это был конец путешествия. Мы прошли через все узлы и ребра.
Разработка алгоритма поиска по глубине-ферту
Перед разработкой алгоритма важно представить приведенную выше диаграмму в виде списка смежности. Если вы раньше не видели список смежности, это словарь. Где каждый узел является ключом, а узлы, которые связаны в нем с исходящими путями, являются значениями в списке.
Посмотрите на список смежности ниже. Узел «u» имеет две исходящие ссылки, ведущие к узлу «v» и узлу «x». Итак, «u» - это ключ, а список с элементами «v» и «x» - это значение. Таким же образом мы должны взять любой другой узел и создать пары ключ-значение.
g = {
'u': ['v', 'x'],
'v': ['y'],
'y': ['x'],
'x': ['v '],
' w ': [' y ',' z '],
' z ': [' z ']
} Список смежности готов.
Я буду использовать метод рекурсии для разработки алгоритма поиска в глубину.
Идея состоит в том, чтобы пройти все узлы и вершины, как мы проходили на рисунках в предыдущем разделе. Чтобы отслеживать посещенные узлы, мы начнем с пустого списка.
class depth_first:
def __init __ (self):
self.visited = []
Теперь определите функцию, которая будет проходить через все узлы, и если есть непосещаемый узел, мы войдем в этот узел и узнаем, где этот узел берет нас.
def dfs (self, graph):
для версии в графике:
, если вер не в self.посещено:
self.dfs_visit (graph, ver)
return self.visited
Обратите внимание, в этой функции мы вызвали функцию «dfs_visit». Эта функция должна пройти весь непосещенный маршрут, предлагаемый непосещенным узлом, и добавить эти непосещенные узлы в список «посещенных». Мы реализуем эту функцию рекурсивно.
Вот функция 'dfs_visit':
def dfs_visit (self, graph, vertex):
, если вершина не в self.visited:
self.visited.append (вершина)
для nb в g [вершина]:
себя.dfs_visit (g, nb)
Внимательно посмотрите! Эта функция добавит узел, если его еще нет в списке «посещенных». Затем он перейдет к соседнему с ним узлу и вызовет себя.
Таким образом, он будет проходить весь маршрут, который ранее не посещался, и по одному.
Вот полный код:
class depth_first:
def __init __ (self):
self.visited = [] def dfs (self, graph):
для ver in graph:
if ver not in self.visited:
сам.dfs_visit (graph, ver)
return self.visiteddef dfs_visit (self, graph, vertex):
, если вершина не в self.visited:
self.visited.append (вершина)
для nb в g [вершина]:
self.dfs_visit (g, nb)
Давайте протестируем это сейчас, используя список смежности, который мы описали ранее.
d = depth_first ()
print (d.dfs (g))
Вывод:
['u', 'v', 'y', 'x', 'w', 'z']
Смотрите, порядок узлов такой же, как мы и ожидали!
Распространенные ошибки, которые люди допускают в алгоритме DFS
Я видел много других веб-сайтов и блогов, которые объясняли алгоритм поиска в глубину.Но код, который использовали многие из них, выглядит следующим образом:
def dfs (graph, vertex, path = []):
path + = [vertex] for n in graph [vertex]:
if n not in path:
path = dfs (graph, n, path)
return path
Если вы заметили, он не перебирает вершины в цикле. Он начинается с исходного узла и продолжает проходить через узлы смежности. Он будет работать на графе, где каждый узел имеет исходящий узел, который соединяется с любым другим посещенным узлом.
Но диаграмма, над которой мы работаем, где узел «y» не имеет исходящей ссылки на «w», этот алгоритм не будет работать.Потому что он никогда не дойдет до буквы «w».
Давайте проверим
print (dfs (g, 'u'))
Вывод:
['u', 'v', 'y', 'x']
Видите, узлы не видны ' w 'и' z '.
Заключение
Я хотел представить и объяснить процесс того, как работает поиск в глубину, и как разработать алгоритм как можно яснее. Надеюсь, теперь вам это легко.
Не стесняйтесь подписываться на меня в Twitter и ставить лайки на моей странице в Facebook.
Дополнительная информация
Решатель лабиринтов DFS python
Для лабиринта, созданного этой задачей, напишите функцию, которая находит (и отображает) кратчайший путь между двумя ячейками. Обратите внимание: поскольку эти лабиринты генерируются алгоритмом поиска в глубину, они не содержат круговых путей, и можно использовать простой поиск по дереву в глубину.
В этой задаче кодирования я пытаюсь реализовать алгоритм поиска пути A *, чтобы найти оптимальный путь между двумя точками в 2D-сетке.Я начинаю с объяснения механизма работы алгоритма, смотрю на псевдокод, а затем пишу алгоритм на JavaScript, используя библиотеку p5.js для рендеринга.
Matka india net недельный график
4 марта 2020 · Создание и решение головоломок судоку с помощью уникального решения на Python с использованием алгоритма поиска в глубину с возвратом. Есть несколько алгоритмов, которые можно использовать для решения головоломок судоку, и в этом посте мы будем использовать алгоритм поиска с возвратом как для генерации, так и для решения головоломок.
V
Nokia lumia
алгоритмы поиска в глубину python. ... Решение лабиринта с помощью DFS против «следования за стеной» ... Новейший поток вопросов поиска в глубину
Неинформированный поиск Реализуйте программу решения лабиринта сетки, которая использует алгоритмы неинформированного поиска для решения сеток. Действия агента движутся в одном из четырех направлений: вверх, вниз, влево и вправо. Каждое действие имеет стоимость шага 1. 31 августа 2020 г. · Решение головоломок с одним решением, например лабиринты. (DFS можно адаптировать для поиска всех решений лабиринта, включив только узлы на текущем пути в посещенный набор.) Генерация лабиринта может использовать рандомизированный поиск в глубину. Поиск связности в графиках. Псевдокод DFS (рекурсивная реализация): ниже показан псевдокод для DFS. В ... Сентябрь 02, 2020 · Поиск в глубину (DFS) использует концепцию обратного отслеживания в самой своей основе. Итак, в DFS мы в основном пытаемся рекурсивно исследовать все пути от данного узла, пока не достигнем цели. После поиска в определенной ветви дерева в DFS мы можем попасть в два возможных состояния. Мы попадаем в состояние цели, и в этом случае просто выходим.
Анимация создания лабиринта 30 на 20 с использованием поиска в глубину. Этот алгоритм представляет собой рандомизированную версию алгоритма поиска в глубину. Этот подход, который часто реализуется с помощью стека, является одним из простейших способов создания лабиринта с помощью компьютера.
Наш агент решает этот лабиринт менее чем за секунду со стоимостью пути 350: python pacman.py -l bigSearch -p ClosestDotSearchAgent -z .5. Подсказка: самый быстрый способ завершить findPathToClosestDot - это заполнить задачу AnyFoodSearchProblem, для которой отсутствует целевой тест.Затем решите эту проблему с помощью соответствующей функции поиска.
P0507 honda crv 2006
5 октября 2010 г. · Мой тщательный поиск все еще не нашел лучшего пути, только путь. Итак, я полностью переписал свой решатель, чтобы использовать поиск в ширину, и он находит кратчайший путь всего за 8,6 секунды. 5 секунд, если я заполняю тупики, но поскольку это занимает 12 секунд, это не победа. Ради интереса, вот тупиковая версия. mazesolver.py Решатель лабиринта java Решатель лабиринта java
V
Как получить клеевой блок при сборке лодки
Полный список см. в codereview.stackexchange.com
Этот проект написан из статьи, написанной в блоге Эриола в контексте проблемы, связанной с вызовом на Python. В другом месте, где много разных видов лабиринтов (история, классификация, генерация, рисолуция, мир и легенда), dove и piacevole perdersi: Maze Generation; Думай Лабиринт: алгоритмы лабиринта; Алгоритм решения лабиринта ... Единственная платформа соревнований по программированию Web 2.0. Время сервера: 27 декабря 2020 г., 19:38:21 (f2). Настольная версия, перейти на мобильную версию.Чтение и запись файлов на Python. На этом этапе у вас должен быть установлен python на вашем компьютере и вы больше не используете trinket.io. Мы рекомендуем установить Anaconda и использовать интегрированную среду разработки Spyder (IDE). Python упрощает чтение и запись текстовых файлов. Общий синтаксис для открытия файла следующий:
Codeforces. Соревнования и соревнования по программированию, сообщество программистов. import java.io. *; import java.util. *; публичный класс Akisolution {публичный статический сканер sc...
PySwip - это мост между Python и SWI-Prolog, позволяющий запрашивать SWI-Prolog в ваших программах Python. Он имеет (неполный) интерфейс иностранного языка SWI-Prolog, служебный класс, который упрощает выполнение запросов с помощью Prolog, а также интерфейс Pythonic.
1480 комплект приводного вала
Поиск по глубине (DFS) - это алгоритм для обхода или поиска в древовидных или графических структурах данных. Каждый начинает с корня (выбирая какой-то произвольный узел в качестве корня в случае графа) и исследует, насколько это возможно, вдоль каждой ветви, прежде чем выполнять обратное отслеживание.Опубликовано 27 ноября 2018 г. Программа Python для решения лабиринтов с использованием алгоритма Breath First Search. BFS - один из наиболее эффективных алгоритмов решения лабиринта. Полный код можно загрузить по адресу ...
V
Miter saw guard
Sudoku Solver (python) играбельная игра в судоку с поиском в глубину для обобщенных nxn головоломок судоку. Tile Maze (C ++)
21 декабря 2020 г. · Алгоритм DFS. Прежде чем изучать код Python для Depth-First и его вывод, давайте рассмотрим алгоритм, которому он следует для того же.Рекурсивный метод алгоритма поиска в глубину реализован с использованием стека. Стандартная реализация поиска в глубину помещает каждую вершину графа в одну во всех 2 категориях: 1) Посещено 2) Не ... Поиск в глубину (DFS) - это алгоритм для обхода или поиска структур данных дерева или графа. Каждый начинает с корня (выбирая какой-то произвольный узел в качестве корня в случае графа) и исследует, насколько это возможно, вдоль каждой ветви, прежде чем выполнять обратное отслеживание. алгоритмы поиска в глубину Python.... Решение лабиринта с DFS против «следования за стеной» ... Новейший поток вопросов поиска в глубину
4 октября 2020 г. · Хеши для алгоритмов-0.1.4-py3-none-any.whl; Алгоритм хеш-дайджеста; SHA256: ee76609fdf99dc3c6f130f3923b77fc12e8636957791caa89e06743d524b4e15: Скопируйте MD5
Dfs Python ... Dfs Python
Используемый John Deere gator частей тела
В этом курсе рассматриваются концепции и идеи современных алгоритмов искусственного интеллекта. игровые движки, распознавание почерка и машинный перевод.Благодаря практическим проектам студенты знакомятся с теорией, лежащей в основе алгоритмов поиска по графам, классификации, оптимизации, обучения с подкреплением и т. Д.
Коды дат впускного коллектора Pontiac
Модификатор зеркала Blender не работает
См. Полный список на laurentluce .com
, если соответствующий вход в лабиринт является допустимым. Наша задача - найти путь от начальной до конечной позиции в лабиринте. Структура данных должна реализовывать ваш решатель лабиринта с тремя отдельными структурами данных position_holder (все из которых реализованы для вас в Python, Jaa, v C и т. Д., Поэтому просто напишите код, предполагающий абстрактную структуру данных... 18 марта 2020 г. · Лабиринт с ключом. Концепция лабиринта такова. Постановка задачи: Помогите Джерри пройти через лабиринт слева направо и вверху, собирая по пути ключ. Путь от источника к месту назначения не должен проходить через какую-либо ячейку не более одного раза. Джерри может двигаться в следующих направлениях: 1. Влево 2. Вправо 3. Вверх 4. Вниз 5. Северо-восток 6. Север ... Очень простая реализация итеративного dfs на языке Python показана ниже (здесь adj представляет представление списка смежности. входного графа): следующие анимации демонстрируют, как работает алгоритм, стек также отображается в разные моменты времени во время выполнения.
Понимание этих методов в Python расширяет ваш потенциал для успеха в веб-разработке, изменении данных, машинном обучении и многом другом. О книге Классические проблемы информатики в Python оттачивают ваши навыки решения задач компьютерной грамотности с помощью проверенных временем сценариев, упражнений и алгоритмов с использованием Python.
Решение проблем с помощью алгоритмов и структур данных с использованием Python Брэдли Н. Миллер, Дэвид Л. Ранум под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Международная лицензия.
Личное имущество в местах общего пользования
Maze Solver Algorithm. Для решения лабиринтов я использовал алгоритм кратчайшего пути Дейкстры, этот алгоритм использует структуру данных очереди приоритетов. Это можно описать следующими шагами. Выберите начальный и конечный узлы, все узлы, кроме начального, имеют бесконечное расстояние. Решатель лабиринта Java Решатель лабиринта Java
V
Программирование передачи 6l90
Поскольку версия в предыдущем посте отстой, я опубликовал новую версию реализация стека.Примечание: используйте встроенную версию для максимальной производительности.
Поскольку версия в предыдущем посте отстой, я опубликовал новую версию реализации стека. Примечание: используйте встроенную версию для максимальной производительности. DFS - Генератор случайных лабиринтов и проект решения: все в EEL 3370 должны пройти модули DFS Project 4 для 10% оценки за курс. Детали отправки включены в инструкции для каждого модуля, ссылки на которые приведены ниже. Поиск в глубину - это алгоритм, который можно использовать для создания лабиринта.Идея действительно проста и легко реализуется с помощью рекурсивного метода или стека. Обычно вы начинаете со случайной точки и продолжаете прокладывать путь в одном из 4 направлений (вверх, вправо, вниз, влево), пока не перестанете двигаться дальше.
DFS - Генератор случайных лабиринтов и проект решения: все в EEL 3370 должны пройти модули DFS Project 4 для 10% оценки за курс. Детали отправки включены в инструкции для каждого модуля, ссылки на которые приведены ниже.
26 августа 2017 · 26 августа 2017 29 ноября 2017 SagnikModak java, решатель лабиринтов, поиск пути, python, экспертная система на основе правил 7 мыслей о «Простом алгоритме поиска пути в JAVA и Python» Pingback: Научитесь программировать Игровой искусственный интеллект на Python менее чем за 10 минут - Часть I - Новые биты
Альтернативы Aveda
Python 的 到头子 到头 了 Python 终于 要 回归 现实 了? @ 所有 程序员 报告 把 Python 的 真相 撕开了! 不 信 你 看 : Python 今年 要 跑路? 三份 报告 炸出 真相.... 人生 苦 短 , 钱多 少 , 快 Python , 这话 曾 是 不少 选择 投入 Python 麾下 的 31 января 2007 г. · Как видно из дизайна UML, класс Maze создает лабиринт и содержит набор ячеек для работы алгоритма. Каждая ячейка содержит массив из 4 стен, которые можно «снести», установив элемент в массиве на ноль. Код для реализации поиска в глубину показан ниже.
Коды сканера полиции ct
Как вручную переместить сиденье с электроприводом ford fusion
23 августа 2020 г. · Python 3 очка знаний.Это типичная проблема, которую можно решить с помощью DFS и BFS (с одинаковой временной сложностью). У меня есть развивающийся пост, который содержит шаблоны для распространенных алгоритмов, включая DFS и BFS. Ниже содержимое извлечено из этого сообщения. Типичный шаблон DFS Python3; #params обычно меняются в каждом раунде dfs
Понимание этих методов в Python расширяет ваш потенциал для успеха в веб-разработке, изменении данных, машинном обучении и многом другом.