Python целая часть от деления: Встроенные функции | Python 3 для начинающих и чайников
Что значит //, %, not in, == и другие операторы Python ~ PythonRu
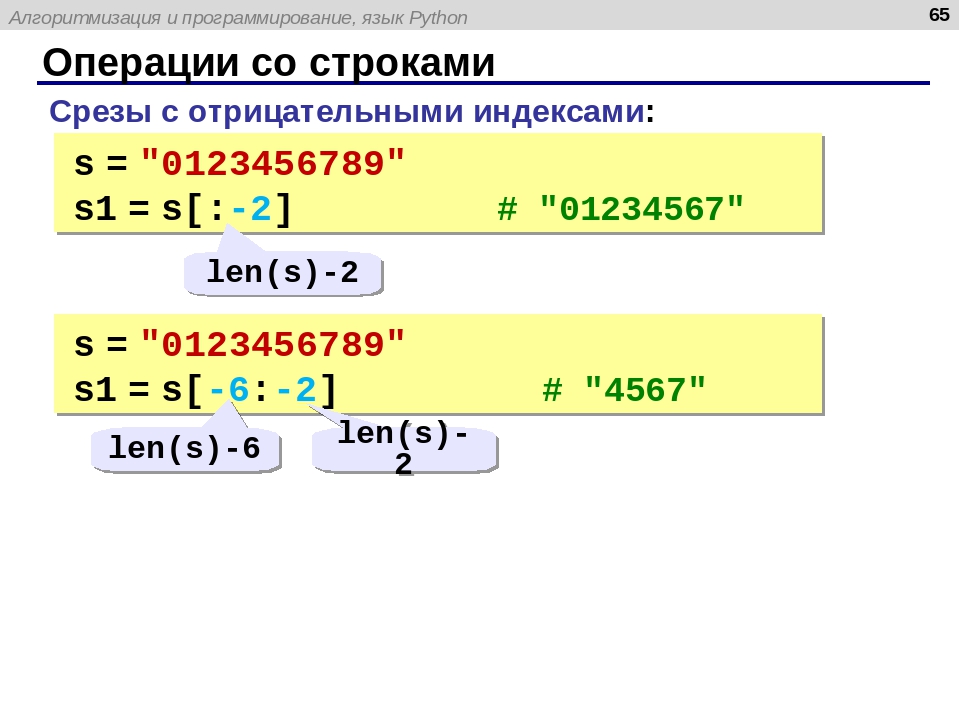
Предыдущий урок: Строки в Python
Операторами пользуются для выполнения операций с переменными и значениями.
Python делит операторы на следующие группы:
- Арифметические операторы
- Операторы присваивания
- Операторы сравнения
- Логические операторы
- Операторы тождественности
- Операторы принадлежности
- Побитовые операторы
Арифметические операторы в Python
Арифметические операторы используются с числовыми значениями для выполнения общих математических операций:
| Оператор | Значение | Пример |
|---|---|---|
| + | добавление | 4 + 5 |
| — | вычитание | 8 — 3 |
| * | умножение | 5 * 5 |
| / | деление | 4 / 2 |
| % | остаток от деления | 7 % 2 |
| ** | возведение в степень | 2 ** 3 |
| // | целочисленное деление | 15 // 4 |
Операторы присваивания в Python
Операторы присваивания используются для присваивания значений переменным:
| Оператор | Пример | Так же как |
|---|---|---|
| = | x = 5 | x = 5 |
| += | x += 3 | x = x + 3 |
| -= | x -= 3 | x = x — 3 |
| *= | x *= 3 | x = x * 3 |
| /= | x /= 3 | x = x / 3 |
| %= | x %= 3 | x = x % 3 |
| //= | x //= 3 | x = x // 3 |
| **= | x **= 3 | x = x ** 3 |
| &= | x &= 3 | x = x & 3 |
| |= | x |= 3 | x = x | 3 |
| ^= | x ^= 3 | x = x ^ 3 |
| >>= | x >>= 3 | x = x >> 3 |
| <<= | x <<= 3 | x = x << 3 |
Операторы сравнения в Python
Операторы сравнения используются для сравнения двух значений:
| Оператор | Значение | Пример |
|---|---|---|
| == | равно | x == y |
| != | не равно | x != y |
| > | больше чем | x > y |
| < | меньше чем | x < y |
| >= | больше чем или равно | x >= y |
| <= | меньше чем или равно | x <= y |
Логические операторы в Python
Логические операторы используются для объединения условных операторов:
| Оператор | Значение | Пример |
|---|---|---|
| and | Возвращает значение True если оба утверждения верны | x < 5 and x < 10 |
| or | Возвращает True если одно из утверждений верно | x < 5 or x < 4 |
| not | Меняет результат, возвращает False если результат True | not(x < 5 and x < 10) |
Операторы тождественности в Python
Операторы тождественности используются для сравнения объектов. Являются ли они одним и тем же объектом с одинаковым местоположением в памяти:
Являются ли они одним и тем же объектом с одинаковым местоположением в памяти:
| Оператор | Значение | Пример |
|---|---|---|
| is | Возвращает true если переменные являются одним объектом | x is y |
| is not | Возвращает true если переменные разные | x is not y |
Операторы принадлежности в Python
Операторы принадлежности используются для проверки того, представлена ли последовательность в объекте:
| Оператор | Значение | Пример |
|---|---|---|
| in | Возвращает True если последовательность присутствует в объекте | x in y |
| not in | Возвращает True если последовательность не присутствует в объекте | x not in y |
Побитовые операторы в Python
Побитовые операторы используются для работы в битовом (двоичном) формате:
| Оператор | Название | Значение |
|---|---|---|
| & | И | Устанавливает каждый бит в 1, если оба бита 1 |
| | | Или | Устанавливает каждый бит в 1 если один из двух битов 1 |
| ^ | только или | Устанавливает каждый бит в 1 если только один из битов 1 |
| ~ | Не | Переставляет все биты |
| << | Сдвиг влево | Сдвигает влево на количество бит указанных справа |
| >> | Сдвиг вправо | Сдвигает вправо на количество бит указанных справа |
Далее: Списки (list)
Арифметические операции в Python. | DOCS-Python.ru
| DOCS-Python.ru
Все числовые типы, кроме сложных, поддерживают следующие операции согласно их приоритетам выполнения:
x + y
Результатом будет сумма чиселxиуx - y
Результатом будет разница чиселxиуx * y
Результатом будет произведение чиселxиуx / y
Результатом будет частное чиселxиуx // y
Результатом будет делениеx / yс округлением результата до ближайшего целого в меньшую сторону. Операцию называют «целочисленным делением».
Результирующее значение является целым целым числом, хотя тип результата не обязательно являетсяint.
Результат всегда округляется до минус бесконечности:1 // 2равно0,(-1) // 2равно-1,1 // (-2)равно-1,(-1) // (-2)равно0.
x % y
Результатом будет остаток от деления чиселx / y.-x
Результатом будет отрицательное значениеx.+x
В результате числоxостанется без изменений.abs(x)
Результатом будет абсолютное значение или величинаx.int(x)
В результате числоxпреобразуется в целое числоint.
В качестве аргумента допускается использовать принятые числовые литералы включающие цифры от0до9или любой эквивалент Юникода.
Преобразование вещественного числа в целое число может округляться или усекаться, как в C. Для четко определенных преобразований используйтеmath.floor()иmath.ceil()float(x)
В результате числоxпреобразуется в число с плавающей точкойfloat.
В качестве аргумента допускается использовать принятые числовые литералы включающие цифры от0до9или любой эквивалент Юникода.
Функция также принимает строки'nan'— не число и'inf'— положительная или отрицательная бесконечность, с необязательным префиксом+или-.complex(real, image)
Результатом будет комплексное число с вещественной частьюreal, мнимой частьюimage.
В качестве аргумента допускается использовать принятые числовые литералы включающие цифры от 0 до 9 или любой эквивалент Юникода.c.conjugate()
Результатом будет сопряженное комплексное числос.divmod(x, y)
Результатом будет пара(x // y, x % y).pow(x, y)
Результатом будет числоxв степениу. Python определяет
Python определяет 0 ** 0как равное1, как это обычно бывает для языков программирования.x ** y
Результатом будет числоxв степениу. Python определяетpow(0, 0)как равное1, как это обычно бывает для языков программирования.
Внимание!. Комплексным числам (тип complex) недоступны операции: // — деление без остатка , % — остаток от деления, int(), float(), divmod().
Примеры использования:
Синтаксис арифметических выражений прост. Операторы +, -, * и / работают так же, как и в большинстве других языков программирования, круглые скобки () могут быть использованы для группировки выражений.
>>> 2 + 2 # 4 >>> 50 - 5*6 # 20 >>> (50 - 5*6) / 4 # 5.0 # деление всегда возвращает тип float >>> 8/5 # 1.6
Целые числа, например 2, 4, 20 имеют тип int, числа с дробной частью, например 5.0, 1.6 имеют тип float.
Деление / всегда возвращает тип float (число с плавающей запятой). Для получения целой части числа, полученного в результате деления (floor division — округление результата до ближайшего целого в меньшую сторону) вы можете использовать оператор //, для расчета остатка вы можете использовать оператор %
# классическое деление >>> 17 / 3 # 5.666666666666667 # целочисленное деление >>> 17 // 3 # 5 # возвращает остаток от деления >>> 17 % 3 # 2
С помощью Python можно использовать оператор ** для вычисления степеней
# 5 в квадрате >>> 5 ** 2 # 25 # 2 в степени 7 >>> 2 ** 7 # 128
Знак равенства = используется для присвоения значения переменной.
>>> width = 20 >>> height = 5 * 9 >>> width * height # 900
Если переменная не определена, т. е. ей не присвоено значение, попытка использовать ее приведет к ошибке.
# переменная 'x' не определена # ей не присвоено значение, а значит # Python ничего про нее не знает >>> x # Traceback (most recent call last): # File "<stdin>", line 1, in <module> # NameError: name 'x' is not defined
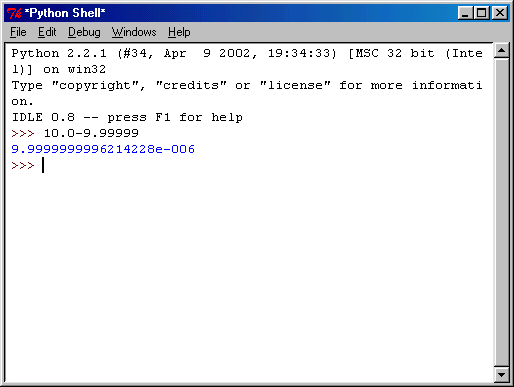
Существует полная поддержка операций с плавающей запятой, операции с числами смешанного типа преобразуют результат в число с плавающей точкой.
В интерактивном режиме последнее печатное выражение присваивается переменной _ — символ подчеркивания. Это означает, что при использовании Python в качестве калькулятора несколько проще продолжить вычисления, например:
>>> tax = 12.5 / 100 >>> price = 100.50 >>> price * tax # 12.5625 >>> price + _ # 113.0625 >>> round(_, 2) # 113.06
Переменная _ должна рассматриваться как доступная только для чтения. Не присваивайте ей явно значение, иначе вы создадите независимую локальную переменную с тем же именем, маскируя встроенную переменную с ее магическим поведением. Эта магическая переменная нередко используется в коде для скрытия неиспользуемых данных.
client = [(1, 'shopkeeper', 'Michael Palin'),
(2, 'client', 'John Cleese'),
(3, 'sketch', 'Cheese Shop Sketch')]
for num, _, name in client:
print(num, name)
# 1 Michael Palin
# 2 John Cleese
# 3 Cheese Shop Sketch
Помимо int и float, Python поддерживает другие типы чисел, такие как Decimal и Fraction. Python также имеет встроенную поддержку комплексных complex чисел и использует суффикс j или J для обозначения мнимой части, например, 3+5j.
Операции над числами в Python.
Числовые операции.
Python поддерживает все обычные операции, выполняемые над числами. Числа — неизменяемые объекты. Выполняя операции над числовыми объектами, вы всегда получаете новые числовые объекты, а не изменяете существующие. Разрешается обращаться к мнимой и действительной частям комплексного объекта
Числа — неизменяемые объекты. Выполняя операции над числовыми объектами, вы всегда получаете новые числовые объекты, а не изменяете существующие. Разрешается обращаться к мнимой и действительной частям комплексного объекта complex как к атрибутам complex.real и complex.imag, доступным только для чтения. Попытка присвоить этим атрибутам новые значения приведет к возбуждению исключения.
Необязательные знаки + и - перед числами, а также знак+, присоединяющий литерал с плавающей точкой к мнимому для образования комплексного числа, не являются частью синтаксиса литералов. Они являются обычными операторами, которые подчиняются обычным правилам, регламентирующим приоритет операторов.
Например, вычисление выражения -2**2 дает результат -4. Возведение в степень имеет более высокий приоритет, чем унарный «минус», поэтому анализатор воспринимает данное выражение как -(2**2) , а не как (-2)**2.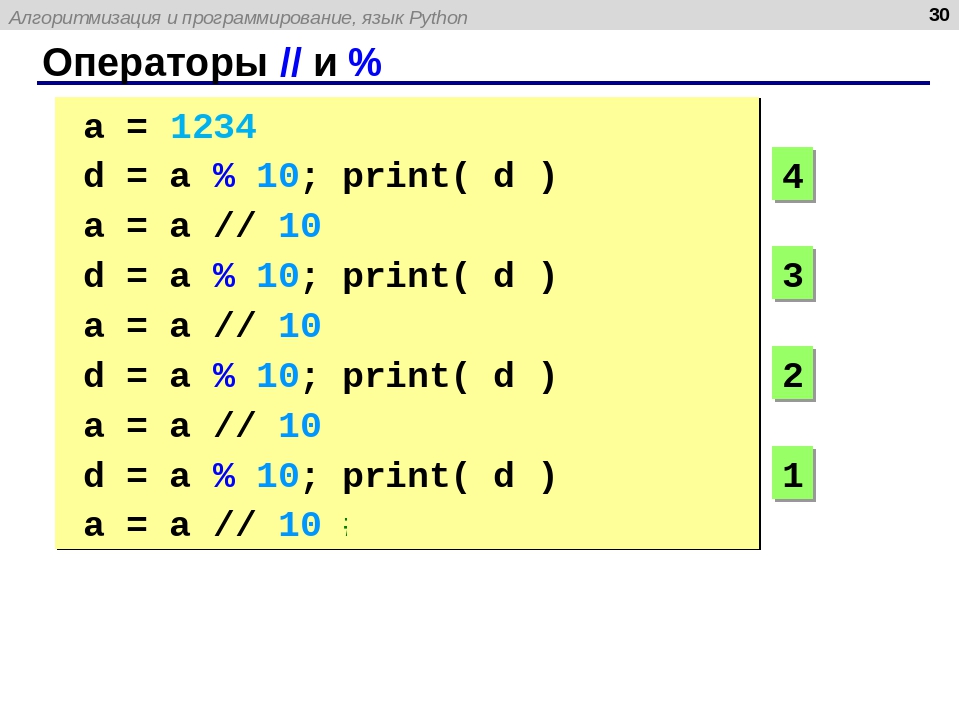
Преобразование типов чисел в Python.
В арифметических операциях и операциях сравнения могут принимать участие любые два числа, относящиеся к встроенным типам Python. Если типы операндов различаются, выполняется автоматическое повышение типов.
Арифметические операции в Python.
Синтаксис арифметических выражений прост. Операторы +, -, * и / работают так же, как и в большинстве других языков программирования. Так же имеются операции целочисленного деления, остатка от деления, возведения в степень
Битовые операции над числами в Python.
Целые числа можно интерпретировать как битовые строки и использовать в битовых операциях. Битовые операторы имеют более низкий приоритет по сравнению с арифметическими операторами
Проблемы и чисел c плавающей запятой.
К сожалению, большинство десятичных дробей не могут быть представлены точно как двоичные дроби. Следствием этого является то, что, как правило, вводимые десятичные числа с плавающей запятой аппроксимируются только двоичными числами с плавающей запятой, фактически сохраненными в машине.
Функции теории чисел модуля math в Python.
Функции относящиеся к теории чисел.
В этом разделе представлены функции относящиеся к теории чисел.
Содержание:
- Факториал числа,
- Наибольший общий делитель целых чисел,
- Функция
math.frexp(), - Функция
math.ldexp(), - Абсолютное значение числа,
- Остаток от деления,
- Получить дробную и целую часть числа,
- Получить точную сумму элементов списка,
- Получить число
xсо знаком числаy, - Сравнение в пределах указанной точности,
- Наименьшее общее кратное целых чисел,
- Следующее значение
floatпослеxпо направлению кy, - Наименьший значащий бит числа
float.
math.factorial(x):
Функция math.factorial() возвращает факториал указанного числа x.
>>> import math >>> math.factorial(5) 120
Данная функция всегда возвращает число типа int и поддерживает длинную арифметику, т.е. величина обрабатываемого числа x и возвращаемого результата ограничивается только возможностями компьютера.
Если x не является целым числом или если x является отрицательным, то будет вызвано исключение ValueError.
Изменено в Python 3.9. Не рекомендуется передавать числа с плавающей запятой с целыми значениями (например, 5.0).
math.gcd(*integers):
Функция math.gcd() возвращает наибольший общий делитель указанных целочисленных аргументов *integers.
>>> import math >>> math.gcd(3886, 9048) # 58 # проверяем >>> 3886/58, 9048/58 # (67.0, 156.0)
- Если какой-либо из аргументов не равен нулю, то возвращаемое значение является наибольшим положительным целым числом, которое является делителем всех аргументов:
- Если все аргументы равны нулю, то возвращаемое значение равно 0.

- функция
math.gcd()вызванная без аргументов возвращает 0.
Указанные числа должны быть целыми типа int, но могут быть как положительными, так и отрицательными:
>>> import math >>> math.gcd(-4, -8) # 4 >>> math.gcd(-4, -8.8) # Traceback (most recent call last): # File "<stdin>", line 1, in <module> # TypeError: 'float' object cannot be interpreted as an integer
Изменено в Python 3.9: Добавлена поддержка произвольного количества аргументов. Раньше поддерживалось только два аргумента.
math.frexp(x):
Функция math.frexp() возвращает кортеж из двух чисел (m, e) таких что x == m*2**e.
>>> import math >>> math.frexp(123) # (0.9609375, 7) >>> 0.9609375*2**7 # 123.0
Число m принадлежит к типу float и всегда является таким, что 0.5 <= abs(m) < 1, даже для тех случаев, когда значением x является произвольная степень двойки. Число
Число e всегда целое число int:
>>> math.frexp(0.25) # (0.5, -1) >>> math.frexp(64) # (0.5, 7)
Если x равен 0, то будет возвращено (0.0, 0).
Данная функция используется тогда, когда представление чисел типа float не должно зависеть от архитектуры машины.
math.ldexp(x, i):
Функция math.ldexp() возвращает значение равное x*2**i, т.е. является обратной к функции math.frexp().
>>> import math >>> math.ldexp(3, 4) # 48.0 >>> math.ldexp(0.125, 8) # 32.0
math.fabs(x):
Функция math.fabs() возвращает абсолютное значение, модуль числа x. Результат всегда тип float.
>>> import math >>> math.fabs(-3) 3.0
Данная функция в отличии от встроенной функции abs() не обрабатывает комплексные числа.
math.fmod(x):
Функция math.fmod() возвращает остаток от деления числа x на число y, вычисленный так, как это определено в библиотеке math языка C.
>>> import math >>> math.fmod(2.23, 0.2) 0.02999999999999986
Данная функция направлена на то, что бы результат был максимально приближен к значению x - n*y для некоторого целого числа n, что бы этот результат имел тот же знак, что и x, что бы разность x - n*y == abs(y).
Для чисел типа float данная функция является предпочтительнее чем команда x%y, которая в свою очередь является предпочтительной для чисел типа int. Так как для некоторых случаев, например при x = -1e-100 и x = 1e100, команда x%y может вообще выдать неправильный результат.
math.modf(x):
Функция math. возвращает кортеж из двух чисел  modf()
modf()(f, w) где f это дробная, а w — целая часть числа x. Результат всегда имеет тип float.
>>> import math >>> math.modf(3) # (0.0, 3.0) >>> math.modf(3.14) # (0.14000000000000012, 3.0)
math.fsum(iterable):
Функция math.fsum() возвращает точную сумму значений в итерируемой последовательности iterable. Возвращаемый результат всегда типа float.
>>> import math >>> sum([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) # 0.9999999999999999 >>> math.fsum([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) # 1.0
Может показаться, что эта сумма будет точной всегда, но на самом деле это не так:
>>> math.fsum([0.3, 0.3, 0.3]) 0.8999999999999999
Многое зависит от сборки компилятора языка C, который используется на данной платформе. Если вам нужны точные арифметические операции с десятичными дробями, то воспользуйтесь модулем
Если вам нужны точные арифметические операции с десятичными дробями, то воспользуйтесь модулем decimal.
math.copysign(x, y):
Функция math.copysign() возвращает число c абсолютным значением x, но со знаком числа y. Возвращаемый результат всегда типа float
>>> import math >>> math.copysign(14, -12) # -14.0 >>> math.copysign(-14, 12) # 14.0
На платформах, которые поддерживают нули со знаком функция math.copysign(1.0, -0.0) возвращает -1.0.
math.isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0):
Функция math.isclose() возвращает True если в пределах указанной точности, числа a и b близки настолько, что их можно считать равными.
>>> import math >>> x = 7 >>> y = 7.000000000000001 >>> x==y # False >>> math.isclose(x, y) # True
Считать числа близкими или нет, определяют два аргумента rel_tol и abs_tol.
Аргумент rel_tol это относительный допуск, определяемый как максимально допустимая разница между числами a и b относительно большего из них по модулю. По умолчанию rel_tol=1e-09, что гарантирует, что числа a и b будут одинаковы, в пределах 9 десятичных цифр. Что бы числа считались равными, если они, допустим, отличаются меньше чем на 0.1%, то достаточно установить rel_tol=0.001, но в любом случае данный параметр, должен быть больше нуля:
>>> y = 7.000001 >>> math.isclose(y, 6.999, rel_tol=0.001) # True
Аргумент abs_tol это минимальный абсолютный допуск. полезен для сравнений, близких к нулю. Значение abs_tol должно быть не меньше нуля.
Данная функция эквивалентна команде abs(a-b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol). Значения
Значения inf, -inf считаются близкими только сами к себе, а NaN не является близким ни к одному значению, включая само NaN.
math.lcm(*integers):
Функция math.lcm() возвращает наименьшее общее кратное указанных целочисленных аргументов *integers.
- Если все аргументы отличны от нуля, то возвращаемое значение является наименьшим положительным целым числом, кратным всем аргументам.
- Если какой-либо из аргументов равен нулю, то возвращается значение
0. - Функция
math.lcm(), вызванная без аргументов возвращает1.
Новое в Python 3.9.
math.nextafter(x, y):
Функция math.nextafter() возвращает следующее значение float после x по направлению к y.
Если x равно y, то функция возвращает y.
Примеры:
math.nextafter(x, math.inf)идет вверх: в сторону положительной бесконечности.math.nextafter(x, -math.inf)идет вниз: в сторону минус бесконечности.math.nextafter(x, 0.0)стремится к нулю.math.nextafter(x, math.copysign(math.inf, x))уходит от нуля.
Новое в Python 3.9.
Смотрите также математическую функцию math.ulp().
math.ulp(x):
Функция math.isclose() возвращает значение наименьшего значащего бита числа float x.
- Если
x—NaN(не число), то вернетx. - Если
xотрицательный, то вернетulp(-x). - Если
x— положительная бесконечность, то вернетx. - Если
xравен нулю, то вернет наименьшее положительное денормализованное представимое числоfloat(меньше минимального положительного нормализованного числаfloat,sys.). float_info.min
float_info.min - Если
xравен наибольшему положительному представимому числуfloat, то вернет значение младшего значащего битаx, так что первое числоfloatменьшеxбудетx - ulp(x). - В противном случае (
x— положительное конечное число) вернет значение младшего значащего битаx, так что первое числоfloatбольшеxравноx + ulp(x).
ULP означает «Единица на последнем месте».
Новое в Python 3.9.
Смотрите также математическую функцию math.nextafter().
Оператор Python // — деление без остатка
Оператор // в Python 3 используется для выполнения деления без остатка.
Это означает, что a // b сначала делит a на b и получает целое частное, отбрасывая остаток. Это означает, что результат a//b всегда целое число.
Примеры
Вот несколько примеров, иллюстрирующих то же самое:
>>> 2 // 3 0 >>> 1.3 // 2 0.0 >>> 1.3 // 1.0 1.0 >>> 3.4 // 1.1 3.0 >>> 3.4 // 1.2 2.0 >>> -1//2 -1 >>> -6 // 2 -3 >>> -6 // -3 2
Это показывает, как оператор // выполняет деление на основе пола, учитывая только целую часть деления, даже для чисел с плавающей запятой.
Выполнение этой операции для неподдерживаемых типов (например, списков и строк) приведет к TypeError , как и для любого другого арифметического оператора.
Перегрузка оператора //
// по умолчанию относится к оператору __floordiv__() , поэтому вы можете выполнить перегрузку оператора, переопределив этот метод ( operator.__floordiv__(a, b) )
Вот пример, который перегружает метод // для целочисленных списков одинаковой длины, выполняя индивидуальное деление на основе пола для каждой пары элементов.
Таким образом, два целочисленных списка [3, 4, 5] и [2, 2, 1] дадут [3//2, 4//2, 5//1] , который является просто списком [1, 2, 5] .
import operator
class MyClass():
def __init__(self, a):
self.a = a
def __floordiv__(self, b):
if isinstance(self.a, list) and isinstance(b.a, list) and len(self.a) == len(b.a):
result = []
# Overload // operator for Integer lists
for i, j in zip(self.a, b.a):
result.append(i // j)
return result
else:
# Perform Default // operation otherwise
return operator.__floordiv__(self.a, b.a)
m = MyClass([3, 4, 5])
n = MyClass([2, 2, 1])
print(m // n)
Вывод
[1, 2, 5]
Вывод
В этой статье мы узнали об операторе деления без остатка //. Мы также узнали о выполнении перегрузки оператора для этого, реализовав operator.__floordiv__(a, b) .
Python Modulo — оператор %, примеры math.fmod()
Оператор модуля Python (%) используется для получения остатка от деления. Операция по модулю поддерживается для целых чисел и чисел с плавающей запятой.
Синтаксис оператора по модулю: a % b . Здесь «a» — дивиденд, а «b» — делитель. Результат — это остаток от деления a на b.
Если и «a», и «b» являются целыми числами, то остаток также является целым числом. Если одно из них является числом с плавающей запятой, результатом также будет число с плавающей запятой.
Пример оператора модуля Python
Давайте посмотрим на несколько примеров оператора по модулю.
1. По модулю с целыми числами
>>> 10 % 3 1 >>> 2 % 2 0 >>>
2. По модулю с поплавком
>>> 9 % 3.0 0.0 >>> 10 % 3.0 1.0 >>>
3. Модульное с пользовательским вводом.
Модульное с пользовательским вводом.
x = input("Please enter first number:\n")
fx = float(x)
y = input("Please enter first number:\n")
fy = float(y)
print(f'{x} % {y} = {fx % fy}')
Когда мы получаем данные, введенные пользователем, они имеют форму строки. Мы используем встроенную функцию float() для преобразования их в числа с плавающей запятой. Вот почему остаток равен 1,0, а не 1.
4. Пример ZeroDivisionError
Если делитель равен 0, оператор по модулю выдаст ZeroDivisionError . Мы можем использовать блок try-except, чтобы поймать ошибку.
a = 10.5
b = 0
try:
print(f'{a} % {b} = {a % b}')
except ZeroDivisionError as zde:
print("We cannot divide by 0")
5. По модулю с отрицательными числами
Оператор модуля Python всегда возвращает остаток, имеющий тот же знак, что и делитель. Это может привести к путанице с выводом.
Это может привести к путанице с выводом.
>>> -5 % 3 1 >>> 5 % -3 -1 >>> -10 % 3 2 >>>
- -5% 3 = (1-2 * 3)% 3 = 1
- 5% -3 = (-1 * -2 * -3)% 3 = -1
- -10% 3 = (2-4 * 3)% 3 = 2
6. Python Modulo math.fmod()
Поведение оператора% с отрицательными числами отличается от поведения библиотеки C. Если вы хотите, чтобы операция по модулю велась как программирование на C, вам следует использовать функцию fmod() математического модуля. Это рекомендуемая функция для получения чисел с плавающей запятой по модулю.
>>> import math >>> math.fmod(-5, 3) -2.0 >>> math.fmod(5, -3) 2.0 >>> math.fmod(-10, 3) -1.0 >>>
- fmod (-5, 3) = fmod (-2 -1 * 3, 3) = -2,0
- fmod (5, -3) = fmod (2-1 * -3, -3) = 2,0
- fmod (-10, 3) = fmod (-1-3 * 3, 3) = -1,0
Перегрузка оператора по модулю
Мы можем перегрузить оператор по модулю, реализовав __mod__() в нашем определении класса.
class Data:
def __init__(self, i):
self.id = i
def __mod__(self, other):
print('modulo function called')
return self.id % other.id
def __str__(self):
return f'Data[{self.id}]'
d1 = Data(10)
d2 = Data(3)
print(f'{d1} % {d2} = {d1%d2}')
Вывод:
modulo function called Data[10] % Data[3] = 1
Коротко о проблемах арифметики с плавающей запятой
Мы используем двоичный формат для хранения значений в компьютерах. Что касается дробей, в большинстве случаев мы не можем представить их в точности как двоичные дроби. Например, 1/3 не может быть представлена в точном двоичном формате, и это всегда будет приблизительное значение.
Вот почему вы можете получить неожиданные результаты при выполнении арифметических операций с числами с плавающей запятой. Это ясно из вывода нижеприведенных операций по модулю.
Это ясно из вывода нижеприведенных операций по модулю.
>>> 9.6 % 3.2 3.1999999999999993
На выходе должно быть 0, потому что 3,2 * 3 равно 9,6. Но значения долей с плавающей запятой не представлены точно, и приближение вызывает эту ошибку. Это тоже видно из этого примера.
>>> 9.6 == 3.2 * 3 False >>>
Таким образом, вы должны проявлять особую осторожность при работе с числами с плавающей запятой. Желательно выполнить округление, а затем сравнить только два числа с плавающей запятой.
>>> round(9.6, 3) == round(3.2 * 3, 3) True
Язык Python — целочисленное деление
Пример
Стандартный символ деления (/) работает по-разному в Python 3 и Python 2, когда применяется к целым числам.
При делении целого числа на другое в Python 3 операция деления x / y представляет собой истинное деление (использует метод __truediv__ ) и дает результат с плавающей запятой. Между тем, та же операция в Python 2 представляет собой классическое деление , округляющее результат до отрицательной бесконечности (также известное как взятие этажа ).
Между тем, та же операция в Python 2 представляет собой классическое деление , округляющее результат до отрицательной бесконечности (также известное как взятие этажа ).
Например:
| Код | Вывод Python 2 | Вывод Python 3 |
|---|---|---|
3/2 | 1 | 1,5 |
2/3 | 0 | 0,6666666666666666 |
-3 / 2 | -2 | -1,5 |
Поведение округления к нулю не рекомендуется в Python 2.2, но остается в Python 2.7 ради обратной совместимости и был удален в Python 3.
Примечание: Чтобы получить результат float в Python 2 (без округления пола), мы можем указать один из операндов с десятичной точкой. Приведенный выше пример 2/3 , который дает 0 в Python 2, должен использоваться как 2 / 3,0 или 2,0 / 3 или 2,0 / 3,0 , чтобы получить 0,6666666666666666
| Код | Вывод Python 2 | Вывод Python 3 |
|---|---|---|
3. | 1,5 | 1,5 |
2 / 3,0 | 0,66666666666666 | 0,6666666666666666 |
-3,0 / 2 | -1,5 | -1,5 | -1,5 | -1,5 |
| Код | Вывод Python 2 | Вывод Python 3 |
|---|---|---|
3 // 2 | 1 | 1 |
2 // 3 | 0 | 0 |
-3 // 2 | -2 | -2 |
3,0 // 2,0 | 1,0 | 1,0 |
2,0 // 3 | 0. 0 0 | 0,0 |
-3 // 2,0 | -2,0 | -2,0 |
Можно явно принудительно принудительно применить истинное разделение или разделение по этажам, используя собственные функции в модуле оператора :
от оператора import truediv, floordiv
assert truediv (10, 8) == 1.25 # эквивалентно `/` в Python 3
assert floordiv (10, 8) == 1 # эквивалентно `//`
Несмотря на ясность и ясность, использование операторных функций для каждого деления может быть утомительным.Часто предпочтительнее изменить поведение оператора /. Обычной практикой является устранение типичного поведения деления путем добавления из __future__ import Division в качестве первого оператора в каждом модуле:
# должен быть первым оператором в модуле
из __future__ импортного подразделения
| Код | Вывод Python 2 | Вывод Python 3 |
|---|---|---|
3/2 | 1. 5 5 | 1,5 |
2/3 | 0,6666666666666666 | 0,66666666666666 |
-3 / 2 | -1,5 | -1,5 |
9000f4 ut__ импорт из __ оператор / представляет истинное разделение и только внутри модулей, которые содержат импорт __future__ , поэтому нет веских причин не включать его во всех новых модулях.
Примечание : Некоторые другие языки программирования используют округление до нуля (усечение), а не округление до отрицательной бесконечности , как это делает Python (т.е. на этих языках -3 / 2 == -1 ). Такое поведение может вызвать путаницу при переносе или сравнении кода.
Примечание по операндам с плавающей запятой : В качестве альтернативы из __future__ import Division можно использовать обычный символ деления / и гарантировать, что хотя бы один из операндов является плавающим: 3/2.. Однако это можно считать плохой практикой. Слишком просто написать  0 == 1,5
0 == 1,5 average = sum (items) / len (items) и забыть привести один из аргументов к float. Более того, такие случаи могут часто не замечаться во время тестирования, например, если вы тестируете массив, содержащий float s, но получаете массив int s в производстве. Кроме того, если тот же код используется в Python 3, программы, которые ожидают, что 3/2 == 1 будет True, не будут работать правильно.
См. PEP 238 для более подробного объяснения того, почему оператор деления был изменен в Python 3 и почему следует избегать разделения в старом стиле.
Дополнительные сведения о делении см. В теме Simple Math .
Язык Python — целое число
Przykład
Standardowy symbol podziału (/) działa inaczej w Pythonie 3 i Pythonie 2, gdy jest stosowany do liczb całkowitych.
Podczas dzielenia liczby całkowitej przez inną liczbę całkowitą w Pythonie 3 operacja dzielenia x / y представительство prawdziwy podział (używa metody Tymczasem ta sama operacja w Pythonie 2 репрезентация klasyczny podział, który zaokrągla wynik w kierunku ujemnej nieskończoności (znanej również jako zabieranie 19 głos.
Na przykład:
| Kod | Dane wyjściowe w języku Python 2 | Dane wyjściowe w języku Python 3 |
|---|---|---|
3/2 | 1 | |
2/3 | 0 | 0,66666666666666666 |
-3 / 2 | -2 | -1,5 |
Zachowanie zaokrąglania do zera by Pythonie 2.2, ale pozostaje w Pythonie 2.7 ze względu na wsteczną kompatybilność i zostało usunięte w Pythonie 3.
Uwaga: Aby uzyskać wynik zmiennoprzecinkowy wynik zmiennoprzecinkowy wzgłędowy.Powyższy przykład 2/3 który daje 0 w Pythonie 2, będzie użyty jako 2 / 3,0 lub 2,0 / 3 lub 2,0 / 3,0 aby otrzymać 0,666627 69 0,666627 900 96625 0,666627 96626 wyjściowe w języku Python 2
3.0 / 2.0 2 / 3.0 9668 -3.0/2 Istnieje również operator podziału podłogi ( // ), który działa w ten sam sposb w obu dersógla dogla do najbliższej liczby całkowitej. (chociaż liczba zmiennoprzecinkowa jest zwracana, gdy jest używana z __floordiv__ ) W obu wersjach operator // odwzorowuje na __floordiv__ .
| Код | Датчанин wyjściowe w języku Python 2 | Датчанин wyjściowe w języku Python 3 |
|---|---|---|
3 // 2 | 1 | 1 |
| 9000 | 0 | 0 |
-3 // 2 | -2 | -2 |
3.0 // 2,0 | 1,0 | 1,0 |
2,0 // 3 | 0,0 | 0,0 |
-3 // 2,0 | -2,0 | -2,0 |
Można jawnie wymusić prawdziwy podział lub podział podłogi za pomocą rodzimych funkcji w module operator :
from operator import truediv, floordiv
assert truediv (10, 8) == 1.25 # эквивалентно `/` в Python 3
assert floordiv (10, 8) == 1 # эквивалентно `//`
Jasne i jednoznaczne użycie funkcji operatora dla każdego działu może być uciążliwe.Często preferenceowana jest zmiana zachowania operatora /. Powszechną praktyką jest excluding typowego zachowania podziału poprzez dodanie from __future__ import Division jako pierwszej Instrukcji w ka kdym module:
# должно быть первым заявлением в модуле
из __future__ импортного подразделения
| Код | Датчанин wyjściowe w języku Python 2 | Датчанин wyjściowe w języku Python 3 |
|---|---|---|
3/2 | 1.5 | 1,5 |
2/3 | 0,66666666666666666 | 0,66666666666666666 |
-3/2 | -1,5 | -1,5 |
из отдела импорта __future__ gwarantuje, że operator / репрезентуй правдзивы подзял и тылко w modułach zawierających import __future__ , więc nie ma istowichłyzónow.
Uwaga : Niektóre inne języki programowania używają zaokrąglania w kierunku zera (obcięcia) zamiast zaokrąglania w dół w kierunku ujemnej języki programowania ujemnej nieskończ. 1 ). Takie zachowanie może powodować zamieszanie podczas przenoszenia lub porównywania kodu.
Uwaga na argumentsy zmiennoprzecinkowe : Zamiast alternatywy from __future__ import Division , można użyć zwykłego symbolu podziału / i upewniejnówe zidenj.0 == 1,5 . Można к jednak uznać za złą praktykę. Po prostu zbyt łatwo jest napisać average = sum (items) / len (items) i zapomnieć rzucić jeden z argumentów na zmienną wartość. Co więcej, takie przypadki mogą często unikać powiadomienia podczas testowania, np. Jeśli testujesz na tablicy zawierającej float ale otrzymujesz tablicę int w produkcji. Dodatkowo, jeśli ten sam kod jest używany w Pythonie 3, programy, które oczekują, że 3/2 == 1 będzie Prawdą, nie będą działać poprawnie.
Zobacz PEP 238, aby uzyskać bardziej szczegółowe uzasadnienie, dlaczego operator podziału został zmieniony w Pythonie 3 i dlaczego należy unikać podziału w starym stylu.
Показать информацию на тему подзарядки można znaleźć w temacie Prosta matematyka .
Почему в Python целочисленное деление этажей
Сегодня меня (снова) попросили объяснить, почему целочисленное деление в Python возвращает нижний предел результата вместо усечения до нуля, как в C.
Для положительных чисел нет ничего удивительного:
>>> 5 // 2
2
Но если один из операндов отрицателен, результат не учитывается, т.е. округляется от нуля (в сторону отрицательной бесконечности):
>>> -5 // 2
-3
>>> 5 // — 2
-3
Некоторых это беспокоит, но на то есть веская математическая причина. Операция целочисленного деления (//) и ее аналог, операция по модулю (%), объединяются и удовлетворяют красивой математической зависимости (все переменные являются целыми числами):
a / b = q с остатком r
так что
b * q + r = a и 0
(при условии, что a и b> = 0).
Если вы хотите, чтобы отношение расширилось на отрицательное значение a (оставив b положительным), у вас есть два варианта: если вы усечете q до нуля, r станет отрицательным, так что инвариант изменится на 0 [обновление: исправлен этот пункт]
В математической теории чисел математики всегда предпочитают последний вариант (см., Например, Википедию). Для Python я сделал тот же выбор, потому что есть несколько интересных приложений операции по модулю, где знак a неинтересен. Подумайте о том, чтобы взять метку времени POSIX (секунды с начала 1970 г.) и превратить ее в время дня.Поскольку в сутках 24 * 3600 = 86400 секунд, это вычисление будет просто t% 86400. Но если бы мы выразили время до 1970 года с помощью отрицательных чисел, правило «обрезать до нуля» дало бы бессмысленный результат! Используя правило пола, все работает нормально.
Другие приложения, о которых я подумал, — это вычисления положения пикселей в компьютерной графике. Я уверен, что есть еще кое-что.
При отрицательном b, кстати, все просто переворачивается, и инвариант становится:
0> = г> б.
Так почему же C этого не делает? Вероятно, оборудование не позволяло этого делать во время разработки C. И оборудование, вероятно, не делало этого таким образом, потому что на самом старом оборудовании отрицательные числа были представлены как «знак + величина», а не как дополнение до двух, используемое в наши дни (по крайней мере, для целых чисел). Моим первым компьютером был мэйнфрейм Control Data, и он использовал дополнение как для целых чисел, так и для чисел с плавающей запятой. Шаблон из 60 единиц означает отрицательный ноль!
Тим Петерс, который знает, где похоронены все скелеты Python с плавающей запятой, выразил некоторое беспокойство по поводу моего желания распространить эти правила на числа с плавающей запятой по модулю.Он, наверное, прав; правило усечения в сторону отрицательной бесконечности может привести к потере точности для x% 1,0, когда x — очень маленькое отрицательное число. Но для меня этого недостаточно, чтобы разбить целое число по модулю, а // с этим тесно связано.
PS. Обратите внимание, что я использую // вместо / — это синтаксис Python 3, который также разрешен в Python 2, чтобы подчеркнуть, что вы знаете, что вызываете целочисленное деление. Оператор / в Python 2 неоднозначен, поскольку он возвращает другой результат для двух целочисленных операндов, чем для int и float или двух float.Но это совершенно отдельная история; см. PEP 238.
Целочисленное деление в языках программирования
У меня есть степень в области математики и информатики, но я все еще не знаю, почему разные языки программирования по-разному оценивают Integer / Integer . На любом калькуляторе, если вы разделите одно целое число на другое, вы получите десятичное число (конечно, нет, если числитель является множителем знаменателя).
Итало Тассо 31 мая 2006 г. Ответ
Ну, есть «действительное деление» и «целочисленное деление».Они разные.
Калькуляторы делают действительное деление. Они берут действительное число, делят его на другое действительное число и возвращают действительное число.
В теории чисел мы работаем только с целыми числами. Итак, у нас есть целочисленное деление. Когда вы делите два числа, у вас есть частное и остаток.
10 div 3 = 3 (частное)
10 mod 3 = 1 (остаток)
3 * 3 + 1 = 10
Определение целочисленного деления: даны два числа a и b, частное и остаток или деление a и b определяется формулами:
b * q + r = a
и
0 <= r (или 0 <= | r | <| b | для отрицательных чисел)
Perl (насколько мне известно) не имеет оператора целочисленного деления (частного), но имеет оператор остатка.В C, Pascal и Python есть обе операции. Но они по-разному относятся к отрицательным числам.
В приведенном выше определении есть два возможных значения r: отрицательное и положительное. В математике мы всегда принимаем положительный результат, но языки иногда принимают отрицательный результат.
C и Паскаль (точнее, gcc и freepascal) усекают деление, а затем вычисляют остаток. Python и Perl, с другой стороны, используют функцию пола вместо усечения.Это вызывает различия в частном и остатке при отрицательном целочисленном делении. Например, разделив 3 на (-2):
a = 3, b = -2
b * q + r = a
(-2) * q + r = 3
0 <= | r | <2
Два возможных решения:
q = -2
r = -1
(-2) * (-2) + (-1) = 3
или
q = -1
r = 1
(-2) * (-1) + (1) = 3
Оба верны. В этом случае Perl и Python выбирают первый (отрицательный остаток), а Паскаль и C выбирают второй (положительный остаток).С другой стороны, если вы сделаете a = -3 и b = 2, Perl и Python выберут положительное значение r, а Паскаль и C — отрицательное значение r.
Брэндон Родс 26 января 2015 Ответить
За красоту и симметрию. Наблюдайте:
>>> [n / 10 для n в диапазоне (-30, 30)]
[-3, -3, -3, -3, -3, -3, -3, -3, -3 , -3, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -1, -1, -1, -1, -1, — 1, -1, -1, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
Операция n / 10 приводит к целым числам в сериях ровно 10 идентичных результатов, за которыми следует следующее целое число. .Если бы -7/10 давал ужасный результат 0, тогда в приведенной выше последовательности было бы 20 нулей подряд вместо 10, что сделало бы это единственное число аномалией в совершенно симметричной последовательности.
Бесконечность в Python — представление бесконечного числа в Python
Бесконечность — это неопределенное число, которое может быть отрицательным или положительным . Число используется как бесконечность; иногда сумма двух числовых значений может быть числовым, но различным образцом; это может быть отрицательное значение или положительное значение .
Используется для сравнения решения в алгоритмах на лучшее решение. Как правило, начальное значение может быть положительной или отрицательной бесконечностью; мы должны позаботиться о том, чтобы никакое входное значение не было больше или меньше.
Бесконечность в Python
В Python нет способа или метода для представления бесконечности как целого числа. Это соответствует фундаментальной характеристике многих других популярных языков программирования. Но поскольку python является динамически типизированным языком, вы можете использовать float (inf) как целое число, чтобы представить его как бесконечность.
Следовательно, в python мы не можем представить бесконечность или можем сказать, что нет способа показать бесконечность как целое число. Но мы можем использовать float (inf) как целое число.
В Python положительная бесконечность и отрицательная бесконечность могут быть представлены как:
- Положительная бесконечность: бесконечность
- Отрицательная бесконечность: -inf
Программа Python для определения положительного и отрицательного числа бесконечности
Пример
# Определить число положительной бесконечности
ptive_inf = float ('инф')
print ('Положительная бесконечность:', ptive_inf)
# Определить отрицательное бесконечное число
ntive_inf = float ('- inf')
print ('Отрицательная бесконечность:', ntive_inf) Выход
Положительная бесконечность: бесконечность
Отрицательная бесконечность: -inf Представление положительной и отрицательной бесконечности с помощью математического модуля
Чтобы определить бесконечное число, вы можете использовать математический модуль python .
Примечание: Это будет работать только с python 3.5 или выше версии python.
Синтаксис:
- Положительная бесконечность: math.inf
- Отрицательная бесконечность: -math.inf
Пример:
# Импортировать математический модуль
импортная математика
# Положительная бесконечность
ptive_inf = math.inf
print ('Положительная бесконечность:', ptive_inf)
# Отрицательная бесконечность
ntive_inf = -математика.инф
print ('Отрицательная бесконечность:', ntive_inf) Выход
Положительная бесконечность: бесконечность
Отрицательная бесконечность: -inf Положительное бесконечное число — наибольшее, и отрицательное бесконечное число — наименьшее всех чисел.
Для сравнения: положительная бесконечность всегда больше любого натурального числа.
(т.е. 0,1,2, ………. + ∞. Положительное целое число и + бесконечность.)
Для сравнения, отрицательная бесконечность меньше отрицательного числа.
(т.е. ∞ -…….- 2, -1,0, 1, .2,3 ……… — отрицательная бесконечность и -целое число.)
Пример:
# Определить число положительной бесконечности
ptive_inf = float ('инф')
если 99999999999999999> ptive_inf:
print ('Число больше положительной бесконечности')
еще:
print ('Положительная бесконечность больше')
# Определить отрицательное бесконечное число
ntive_inf = float ('- inf')
если -99999999999999999> ptive_inf:
print ('Число меньше отрицательной бесконечности')
еще:
print ('Отрицательная бесконечность меньше') Выход
Положительная бесконечность больше
Отрицательная бесконечность меньше Программа Python для проверки бесконечности числа
Пример:
импорт математики
# Определить положительное бесконечное число
ptive_inf = float ('инф')
print ('Переменная бесконечна:', math.isinf (ptive_inf))
# Определить отрицательное бесконечное число
ntive_inf = float ('- inf')
print ('Переменная бесконечна:', math.isinf (ntive_inf))
Щелкните и перетащите, чтобы переместить Выход:
Variable is Infinity: True
Переменная - бесконечность: True В приведенном выше примере мы используем метод isinf математической библиотеки, чтобы проверить, является ли число бесконечным или нет.
Представление положительной и отрицательной бесконечности с помощью десятичного модуля
Вы можете определить положительную и отрицательную бесконечность, используя десятичный модуль.
Синтаксис:
- Положительная бесконечность: десятичная дробь (бесконечность)
- Отрицательная бесконечность: десятичная дробь (‘- бесконечность’)
Пример:
из десятичного числа Импорт Десятичный
импортная математика
# Определить положительную бесконечность
ptive_inf = десятичный ('бесконечность')
print ('Переменная бесконечна:', math.isinf (ptive_inf))
# Определить отрицательную бесконечность
ntive_inf = десятичный ('- бесконечность')
print ('Бесконечная переменная:', math.isinf (ntive_inf))
Щелкните и перетащите, чтобы переместить Выход:
Variable is Infinity: True
Переменная бесконечность: True Представьте положительную и отрицательную бесконечность с помощью библиотеки Numpy
Вы можете определить положительную и отрицательную бесконечность с помощью модуля inf библиотеки NumPy
Синтаксис:
- Положительная бесконечность: np.inf
- Отрицательная бесконечность: -np.инф
Пример:
импортировать numpy как np
импортная математика
# Определить положительное число бесконечности
ptive_inf = np.inf
# Проверяем бесконечное число
print ('Положительное бесконечное число:', ptive_inf)
# Определить отрицательное число бесконечности
ntive_inf = -np.inf
# Проверяем бесконечное число
print ('Отрицательное бесконечное число:', ntive_inf) Выход:
Число положительной бесконечности: inf
Число отрицательной бесконечности: -inf Проверить, равно ли положительное число бесконечности числу отрицательной бесконечности
Вы можете просто проверить, равно ли положительное число бесконечности отрицательному числу бесконечности, используя простой оператор «==» , и результат всегда будет ложным.
Пример:
импорт математики
# Определить положительное бесконечное число
ptive_inf = float ('инф')
# Определить отрицательное бесконечное число
ntive_inf = float ('- inf')
print ('Положительная бесконечность равна отрицательной бесконечности:', ptive_inf == ntive_inf) Выход:
Положительная бесконечность равна отрицательной бесконечности: ложь Арифметические операции с бесконечным числом дают бесконечное число
Если вы выполните любую арифметическую операцию с числами положительной или отрицательной бесконечности, результатом всегда будет бесконечное число.
Пример:
# Определить положительное бесконечное число
ptive_inf = float ('инф')
# Умножение положительного числа бесконечности на 5
print ('Умножение:', ptive_inf * 5)
# Добавление к положительному числу бесконечности
print ('Дополнение:', ptive_inf + 5)
# Вычитание до положительной бесконечности Number
print ('Вычитание:', ptive_inf - 5)
# Деление на положительную бесконечность Число
print ('Деление:', ptive_inf / 5)
# Определить отрицательное бесконечное число
ntive_inf = float ('- inf')
# Умножаем отрицательное число бесконечности на 5
print ('Умножение:', ntive_inf * 5)
# Дополнение к отрицательному числу бесконечности
print ('Дополнение:', ntive_inf + 5)
# Вычитание до отрицательной бесконечности Число
print ('Вычитание:', ntive_inf - 5)
# Деление на отрицательную бесконечность Число
print ('Подразделение:', ntive_inf / 5) Выход:
Умножение: inf
Дополнение: inf
Вычитание: inf
Подразделение: inf
Умножение: -inf
Дополнение: -inf
Вычитание: -inf
Деление: -inf
математических операторов Python и порядок операций PEMDAS
Самый быстрый способ выучить правила математики — разбить примеры в
ваш собственный интерпретатор Python.
- Основные операции — Просмотрите заметки схемы.
- PEMDAS — Рассмотрите шесть основных математических операторов.
и познакомим вас с интерпретатором Python. - Целые числа и числа с плавающей запятой — Посмотрите разницу между
целые числа и числа с плавающей запятой. - Практика — Сложите все вместе с домашним заданием
проблема. - Далее: операторы — Представьте реляционные операторы.
Пол Алан Дэвис, 13 марта 2017 г.
Обновлено:
11 августа 2018 г.
Учитесь на практике. Пришло время получить ваш интерпретатор Python и попрактиковаться.
Схема
Назад
следующий
~ / домой
/ tech
/ полный стек
Математические операторы / python
Изучите правила математики в Python, включая PEMDAS
Новичок
Видеоурок
Математические операторы Python и порядок операций PEMDAS | Python для
Новички (4:50)
Видео также можно найти на нашем
Плейлист Full Stack 3 на YouTube.
Примеры кода и видео скрипт
Добро пожаловать. Сегодняшний вопрос: каковы правила математики в Python?
Я Пол, и многие из нас изучают правила математики сначала на бумаге, затем
в калькуляторе, а затем в электронной таблице, и все это было очень
проще, чем на языке программирования. По крайней мере, вот что я нашел.
Итак, я надеюсь сделать ваше путешествие менее трудным, чем мое,
выделение семи стандартных операций Python.
В средней школе в Калифорнии мы используем PEMDAS для запоминания порядка
операций для математики, и мы посмотрим, соответствует ли Python.
Мы поговорим о двух числовых типах данных: целые числа и числа с плавающей запятой, и
посмотрим, как мы поддерживаем их на практике с помощью Python.
(Команды в Linux)
(Уроки Python)
-
# -
() -
** -
* -
/ -
// -
+ -
– -
выход ()
Далее мы рассмотрим другую тему математики: операторы отношения.
Шаг 1. Основы математики с использованием операторов Python
В Project 3 (Python для начинающих) мы установили
python3 а теперь мы углубимся в то, что
Для меня это самая захватывающая часть — обучение Python.
paul @ fullstack: на ~ $ меньше заметок / video0023.txt
Направляясь к Терминалу, давайте рассмотрим PEMDAS , который
означает круглые скобки, показатель степени, умножение, деление, сложение
и вычитание.
Правила математики в Python 3 (видео 23)
Порядок работы — PEMDAS
1. Круглые скобки ()
2. Показатель степени **
3. Умножение *
4. Деление / //%
5. Дополнение +
6. Вычитание —
Примечания:
— после заказа PEMDAS слева направо
— используйте круглые скобки для переопределения порядка
Основные числовые типы данных
— целое число
— float (с плавающей запятой, десятичный)
Примечания:
— любой ввод float приводит к float
— в Python 3 деление приводит к float
— целые числа приводят только к целым числам (кроме деления)
Примечания / видео0023.txt (КОНЕЦ)
В нем подробно описан порядок операций, а также обратите внимание, что в Python у нас есть
три типа деления, регулярное деление, деление по этажам и нахождение
остаток по модулю.
Шаг 2 — Порядок работы Python PEMDAS
Давайте перейдем к python3
Устный перевод и все остальное.
Первый способ взаимодействия с Python выглядит так: одна строка на
время.Во-вторых, это скрипт или текстовый файл, который будет в центре внимания будущего.
Проект.
Итак, три символа больше, чем
>>> — подпись Python,
как командная строка в Linux, то есть она ждет нас.
paul @ fullstack: ~ $ python3
Python 3.4.2 (по умолчанию, 8 октября 2014 г., 10:45:20)
[GCC 4.9.1] в Linux
Для получения дополнительной информации введите «помощь», «авторские права», «кредиты» или «лицензия».
>>> #PEMDAS назад
…
Хеш-символ # или комментарий тоже
аналогично, что означает, что остальная часть строки игнорируется.
Три точки ... — продолжение
подсказка, означающая, что Python недостаточно, чтобы действовать.
Python Вычитание
Итак, начнем с последней буквы PEMDAS, вычитание, дайте
простой 1-2 .
… 1-2
-1
>>>
И вуаля -1 .
Дополнение Python
Затем A для сложения. Мы могли войти
1 + 1 нравится, и работает.
>>> 1 + 1
2
Или 1 +1 вот так, и тоже работает.
>>> 1 +1
2
Или 1 + четыре пробела
1 .
>>> 1 + 1
2
И это тоже работает, но предпочтительнее ставить пробел между
каждый.
>>> 1 + 1
2
Шаг 3. Целые числа и числа с плавающей запятой
Отделение Python
Далее D, деление, и здесь следует упомянуть типы данных: целые числа.
и плавает. До сих пор мы играли с целыми числами. Давай попробуем
число с плавающей запятой, например 6.0
делится на целое число 2 .
>>> 6.0 / 2
3.0
И получаем 3,0 , поплавок.
Python автоматически интерпретирует формат полученного
число в зависимости от того, как вы вводите числа. Итак, ввод любых результатов с плавающей запятой
в поплавке.
>>> 6/2
3.0
Также с делением в Python 3, по крайней мере, что-то вроде целого числа
6 деленное на целое число
2 , равно float
3.0 .
Деление этажа округляется вниз, поэтому
7 этаж, разделен на
3 — это два и третий
( 2,3333333333333335 ).
>>> 7/3
2,3333333333333335
>>> 7 // 3
2
Питон этажный отдел
И 7 , этаж разделен на
3 это
2 , который игнорирует остаток.
Python по модулю деления
Чтобы увидеть только остаток, мы используем модуль или знак процента.
% .
>>> 7% 3
1
Итак, 7% 3 — это
1 потому что 3 переходит в 7 дважды
с одним оставшимся.
Modulo может помочь нам определить, является ли число положительным или отрицательным.
Python умножение
Далее, M, умножение довольно простое, поэтому два целых числа
5 с равно
25 .
>>> 5 * 5
25
И одно целое число 5 и одно число с плавающей запятой
5.0 равно float
25,0 .
>>> 5 * 5,0
25,0
Степень или степень Python
Затем E для экспоненты вводится с двумя звездочками.
** , поэтому
2 во второй степени
4 .
>>> 2 ** 2
4
А в третьей степени — 8 .
>>> 2 ** 3
8
Сколько будет 9 в степени
.5 , или половинной степени?
>>> 9 ** .5
3.0
Помните, что это (число в степени 1/2) — квадратный корень.
Скобки Python
Далее P для скобок. Итак, соблюдая правила эксплуатации
Python будет работать слева направо.
Итак, мы знаем, что 1 + 2 * 4 собирается
дайте нам другой ответ, чем
(1 + 2) * 4 . Правильно?
>>> 1 + 2 * 4
9
>>> (1 + 2) * 4
12
Шаг 4. Практикуйтесь с домашним заданием Python
Я попрошу вас сделать последнее за домашнее задание.
>>> 5 + (4-2) * 2 + 4% 2-4 // 3 — (5-3) / 1
Сделайте это вручную на бумаге перед использованием Python, и есть пара
маленькие хитрости, которые укрепят ваше понимание.Чувствовать
можно поставить на паузу или перемотать назад.
И оставить тип Python Interpreter
exit () , за которым следует
Введите .
>>> выход ()
paul @ fullstack: ~ $
Шаг 5 — Далее: операторы отношения Python
Приглашаем вас присоединиться к нашему путешествию в науку о данных, поскольку мы
шаг за шагом и создайте наш полный стек.
- Клиент : HTML, CSS, JavaScript
- Программное обеспечение : Python Scientific Stack
- Данные : PostgreSQL, MySQL
- ОС : Linux (командная строка), Debian
И наш следующий шаг — поговорить об операторах отношения.
 | DOCS-Python.ru
| DOCS-Python.ru

 Python определяет
Python определяет  0
# деление всегда возвращает тип float
>>> 8/5
# 1.6
0
# деление всегда возвращает тип float
>>> 8/5
# 1.6
 06
06
 factorial(5)
120
factorial(5)
120

 isclose(x, y)
# True
isclose(x, y)
# True
 float_info.min
float_info.min 3 // 2
0.0
>>> 1.3 // 1.0
1.0
>>> 3.4 // 1.1
3.0
>>> 3.4 // 1.2
2.0
>>> -1//2
-1
>>> -6 // 2
-3
>>> -6 // -3
2
3 // 2
0.0
>>> 1.3 // 1.0
1.0
>>> 3.4 // 1.1
3.0
>>> 3.4 // 1.2
2.0
>>> -1//2
-1
>>> -6 // 2
-3
>>> -6 // -3
2
 Модульное с пользовательским вводом.
Модульное с пользовательским вводом. 0 / 2,0
0 / 2,0