Распутыватель нейронных сетей: Кусок керамики научил нейронную сеть забывать по-человечески

Кусок керамики научил нейронную сеть забывать по-человечески

История компьютерных имитаций нервной системы так же стара, как история компьютеров. Тёплую ламповую нейронную сеть соорудил ещё Марвин Минский в 1951 году.

Сейчас подобные сети распознают изображения, переводят текст, прогнозируют погоду и курсы акций, даже готовят для юристов черновики документов. Кибернетических мыслителей научили обыгрывать в го сильнейших игроков на планете (между прочим, эта игра даётся компьютерам куда труднее, чем шахматы), оценивать качество фотографий, искать новые лекарства и делать много других интересных и полезных вещей.

Такие способности нейронной сети придаёт её природа: она имитирует работу нервной системы. Напомним, что нейроны, получив на входе новые данные, »голосуют» за то или иное решение. »Обмен мнениями» происходит через межнейронные соединения – синапсы, которые могут иметь разную пропускную способность. В зависимости от проводимости отдельных синапсов голоса разных нейронов получают разный вес. Если в результате было выработано правильное решение, »распределение ролей» закрепляется, если нет – ищется новое.

Постепенно складывается всё более удачная карта проводимости межнейронных соединений, правильные ответы появляются всё чаще и чаще. В случае с компьютерами этот процесс называется самообучением сети. В общих чертах картина выглядит так, хотя может сильно разниться в деталях в зависимости от заложенной в устройство конкретной модели обучения.

Всё это весьма напоминает процесс обучения живого мозга. Характерно, что сеть, в отличие от классического компьютера, не нуждается в программе, по пунктам расписывающей, как достичь результата. Она действует путём проб и ошибок, запоминая удачные решения. Это и позволяет возложить на кибернетический мозг задачи, которые с трудом поддаются алгоритмизации и долго считались исключительной прерогативой человека.

Но между искусственной и естественной нервной системой есть важные различия. У машин каждая новая порция данных может изменить любой синапс, и в результате фрагмент уже накопленного опыта может быть внезапно утрачен.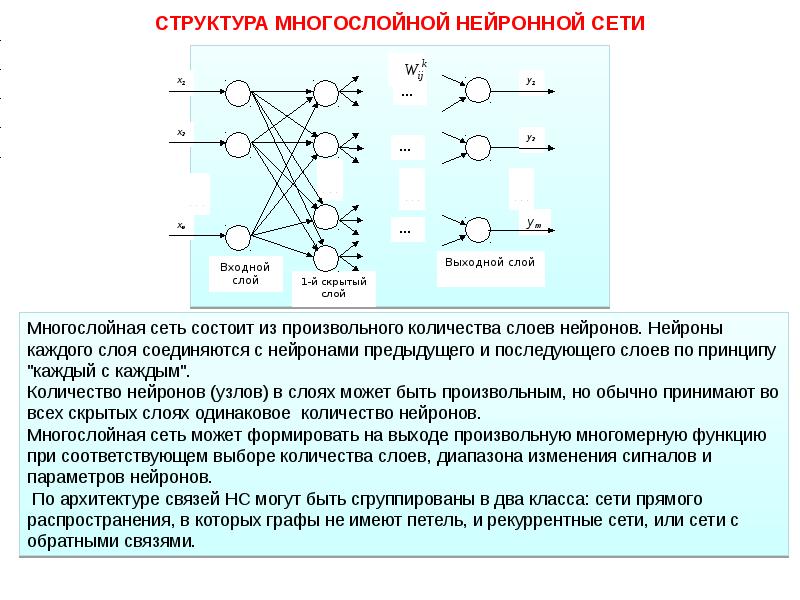 Это явление называется катастрофическим забыванием. С ним борются, снова и снова подавая в нейронную сеть одну и ту же информацию. Такое повторение пройденного впустую расходует рабочее время сети, что, конечно, непрактично. Это мало похоже на поведение нашего мозга, который утрачивает невостребованные навыки медленно и постепенно, а не внезапно и в результате обучения чему-то новому.

Решение пришло с неожиданной стороны. Группа исследователей во главе с Фанем Цзо (Fan Zuo) из Университета Пердью изучала, как керамический материал, представляющий собой соединение самария, никеля и кислорода (химическая формула SmNiO₃), реагирует на газообразный водород. Ни в чём не повинному веществу устраивали водородные ванны по замысловатому сценарию: сначала резко повышали концентрацию водорода в среде, потом так же быстро возвращали её к первоначальному уровню и через некоторое время повторяли процедуру. Как отмечают авторы, это напоминает периодическую подачу сигнала, вроде звонка или вспышки света.

Исследователи помнят, как важно правильно забывать.

Когда атомы водорода проникали в материал, электрические свойства последнего скачкообразно менялись. Через некоторое время газ улетучивался, и параметры вещества возвращались к прежним значениям до следующего «водородного шока». Но вот что интересно: отклик на каждый следующий импульс был всё меньше и меньше.

Учёные усмотрели в этом сходство с привыканием – простейшей формой обучения, которая характерна даже для слизней и мушек-дрозофил. Если сигнал повторяется снова и снова, мы перестаём его замечать, воспринимаем как фон. Это весьма полезное умение: много ли было бы проку от наших органов чувств, если бы мы чувствовали запах кислорода или вздрагивали от каждого такта тикающих часов?

Вдохновлённые сходством процессов столь разной природы, учёные присмотрелись к своему «подопытному» внимательнее. Воздействие водорода на привыкающий к нему материал было исчерпывающе изучено как теоретически, так и экспериментально. Обобщив полученные данные, исследователи продолжили аналогию с нервными процессами и предложили новую модель обучения нейронной сети. Оказалось, что она не страдает от внезапных приступов амнезии, доставляющих столько хлопот при обычных методиках обучения.

Чтобы проверить это, учёные собрали две одинаковые сети из девяти нейронов. Одну из них обучали обычным способом, а другую по новому алгоритму. Задание было, на человеческий взгляд, простым: научиться распознавать три цифры. Сначала обе сети тренировали узнавать цифру 0, потом –цифру 1 и, наконец, цифру 2.

Обычная нейронная сеть, как только её стали учить распознавать единицу, моментально разучилась видеть ноль – ведь картина проводимости синапсов, сформированная для предыдущей задачи, была совершенно бесполезна для нынешней. Вот оно, «катастрофическое забывание» в действии. А вот сеть, обучаемая по экспериментальному алгоритму, освоилась с единицей, ничуть при этом не забыв, как выглядит ноль. Это уже куда больше напоминает нервные процессы живого существа – кто бы мог подумать, что их удастся смоделировать, изучая реакцию керамического материала на водород.

Правда, когда сеть стали учить распознавать двойку, она всё-таки утратила память о нуле, но исследователи связывают это с её ограниченным объёмом – как-никак всего девять нейронов. В нашем мозге их сотни миллиардов, и то мы порой забываем выключить чайник.

Научная статья с результатами исследования опубликована в журнале Nature Communications.

метод борьбы с переобучением нейронной сети

Мы подошли к
моменту, когда нужно поподробнее познакомиться со способами борьбы с
переобучением НС. Это довольно частый эффект, который возникает из-за слишком
точной подгонки разделительной гиперплоскости под обучающие данные. Ранее я уже
приводил иллюстрацию такой подстройки, когда вместо прямой разделяющей линии
формируется кривая. И это приводит к дополнительным ошибкам на тестовых
обучающих множествах, т.е. на примерах, которые не участвовали при обучении.

Упрощенно,
эффект переобучения можно представить следующим образом. Предположим, что мы
читаем текст. Мозг среднестатистического человека устроен так, что мы хорошо
воспринимаем слова, даже если буквы в них написаны не по порядку (кроме первой
и последней):

Так вот, если НС
из-за большого числа нейронов подстроится под каждую букву слова, то этот текст
для нее будет совершенно нечитаемым. Но сеть с небольшим числом нейронов,
которая воспринимает слово в целом, сохранит способность к обобщению и
правильному распознаванию.

Но как в
процессе обучения мы можем понять: происходит переобучение или нет? Мы об этом
уже говорили на одном из предыдущих занятий и отмечали, что один из критериев –
это увеличение расхождения в точности выходных значений между данными обучающей
выборки и проверочной:

Отсюда получаем
первую рекомендацию по борьбе с переобучением:

Рекомендация №1:
если наблюдается расхождение в точности выходных значений между обучающей и
проверочной выборками, то процесс обучения следует остановить и уменьшить число
нейронов.

Но это не всегда
дает желаемые результаты. Не редко с уменьшением числа нейронов уменьшается и
точность выходных значений, то есть, показатель качества работы нейросети
ухудшается. Очевидно, в таких случаях с переобучением нужно бороться с
сохранением числа нейронов. Но как это сделать? Здесь нам на помощь приходит
алгоритм под названием

Dropout

На русский язык
его переводят как «метод прореживания» или «метод исключения» или же просто,
говорят «дропаут».

Цель этого
метода – снизить специализацию каждого отдельного нейрона и сделать из них
«специалистов более широкого профиля».  Именно в этом корень проблемы
переобучения. Но как уменьшить специализацию, сохраняя прежнее число нейронов? Очень
просто. Давайте снова представим, что в некоторой школе работают учителя по
различным предметам: химия, биология, история, математика, физика, география и
информатика. Это их специализация. Затем, в какой-то момент времени директор
школы озаботился их приверженностью только одной дисциплине и решил расширить
горизонты их деятельности. Что он сделал? Он заставил учителя по химии время от
времени вести занятия по физике, учителя по физике – химию, математика менялась
с информатикой, а биология, история и география – между собой. В итоге,
учителям волей-неволей пришлось изучить смежные дисциплины и расширить свою
специализацию. Теперь, директор школы был доволен и знал, если какой-то
отдельный учитель заболеет или уволится, у него будет кем его заменить.

Теперь, осталось
понять, как проделать тот же фокус с нейронами нейронной сети? Как в процессе
обучения им «сказать», чтобы они брали на себя функции других нейронов? Решение
просто до гениальности: на каждой итерации изменения весовых коэффициентов часть
нейронов нужно исключать с заданной вероятностью p:

Это эквивалентно
ситуации, когда часть учителей заболела и остальные вынуждены их заменять. Причем,
в следующий момент, уже другие учителя уходят на больничный, а оставшиеся их
заменяют. В результате, расширяется специализация всех учителей школы. Именно
это происходит с нейронами в алгоритме dropout, которые то
выключаются, то включаются. В какой же момент происходит их переключение? Как я
выше отмечал – на каждой итерации изменения весов. Например, если веса меняются
после каждого mini-batch, значит,
переключение происходит после него. Если же веса меняются при каждом новом
наблюдении, значит и переключение происходит с той же частотой. И так далее, то
есть, мы переключаемся после каждой корректировки весовых коэффициентов.

После того, как
сеть обучена, включаются все нейроны и эффект переобучения (излишней
специализации) должен заметно снизиться.

Некоторые из вас
здесь могут заметить одно важное несоответствие. Когда в процессе обучения с
частью выключенных нейронов, мы пропускаем входной сигнал, то число входных
связей на каждом нейроне уменьшается пропорционально вероятности p:

В режиме
эксплуатации значение на входе нейрона будет x, а в момент
обучения значение:

Как вы
понимаете, это приводит к искаженным входным значениям, а значит, и к неверным
результатам на выходе всей НС. Как поправить ситуацию, чтобы, в среднем, эти
суммы были равными? Для этого нужно вычислить среднее число выключенных
нейронов в текущем слое. Пусть их будет n штук. А понятие
среднего в теории вероятностей – это математическое ожидание, которое в
дискретном случае определяется выражением:

У нас роль СВ X играет число
исключенных нейронов в текущем слое;  -
вероятность выключения;  -
число нейронов, к которым применяется эта вероятность. Получаем среднее
значение:

А среднее число
оставшихся нейронов, будет равно:

где q – вероятность
того, что нейрон останется (не будет исключен). Отсюда получаем, что средний
суммарный сигнал на входах нейронов следующего слоя, в среднем, будет меньше на
величину:

И из этого
выражения хорошо видно, что для сохранения масштаба суммы, ее нужно разделить
на величину q:

Во многих
фреймворках алгоритм Dropout реализован именно так: суммарный
сигнал на входах нейронов масштабируется, эмулируя поведение полной сети со
всеми нейронами. Благодаря этому, в среднем, выходной сигнал сети соответствует
истинным значениям и при ее эксплуатации (со всеми включенными нейронами) не
будет возникать «сюрпризов».

Итак, мы
приходим ко второй рекомендации в борьбе с переобучением:

Рекомендация №2:
если наблюдается переобучение и сокращение числа нейронов недопустимо (по тем
или иным причинам), то следует попробовать метод Dropout.

Здесь остается
один открытый вопрос: как выбирать значение вероятности p? Авторы этого
подхода рекомендуют для нейронов скрытого слоя начинать со значения p=0,5. От себя
добавлю, что, затем, при необходимости можно пробовать значения 0,4 и 0,3.

Также следует
иметь в виду, что это не абсолютное средство: оно может как помочь, так и не помочь.
Если эффекта нет, то от него лучше отказаться и искать другие пути выхода из
сложившейся ситуации. И добавлять его в НС только в случае возникновения
проблем с переобучением. Моя рекомендация: просто так сразу, изначально его
применять не нужно, только при описанных проблемах.

Реализация Dropout в Keras

Используемый
нами пакет Keras, для построения
и обучения НС позволяет применять алгоритм Dropout к любому отдельному
слою. Для демонстрации его работы я смоделировал искусственный пример
переобучения распознавания цифр. Взял маленькую обучающую выборку в 5000
изображений. Столько же отвел для проверочной. Число нейронов скрытого слоя
установил в 300 – это явно много для таких выборок и такой задачи. Неизбежно
должны возникнуть проблемы при обучении. Так и происходит. После 50 эпох мы
видим расходящиеся графики:

Теперь, применим
к скрытому слою из 300 нейронов алгоритм Dropout с параметром p=0,8 (я
специально взял его таким большим, чтобы был виден эффект):

model = keras.Sequential([
    Flatten(input_shape=(28, 28, 1)),
    Dense(300, activation='relu'),
    Dropout(0.8),
    Dense(10, activation='softmax') ])

То есть, мы записываем
Dropout после слоя, к которому
он применяется. Теперь после обучения у нас возникает следующая картина:

Смотрите, здесь
качество обучения на проверочной выборке уже не ухудшается и составляет
величину, примерно, 0,22. Тогда как в предыдущем случае она почти достигала
значения 0,3. Dropout здесь явно
сыграл свою положительную роль.

Конечно, это
довольно искусственный, гипертрофированный пример, но он наглядно демонстрирует
эффект уменьшения степени специализации отдельных нейронов и повышения качества
обучения при сохранении общего числа нейронов сети.

Пишем нейросеть на Python с нуля

Статья публикуется в переводе, автор оригинального текста Victor Zhou.

***

Термин «нейронные сети» сейчас можно услышать из каждого утюга, и многие верят, будто это что-то очень сложное. На самом деле нейронные сети совсем не такие сложные, как может показаться! Мы разберемся, как они работают, реализовав одну сеть с нуля на Python.

Эта статья предназначена для полных новичков, не имеющих никакого опыта в машинном обучении. Поехали!

1. Составные элементы: нейроны

Прежде всего нам придется обсудить нейроны, базовые элементы нейронной сети. Нейрон принимает несколько входов, выполняет над ними кое-какие математические операции, а потом выдает один выход. Вот как выглядит нейрон с двумя входами:

Внутри нейрона происходят три операции. Сначала значения входов умножаются на веса:

Затем взвешенные входы складываются, и к ним прибавляется значение порога b:

Наконец, полученная сумма проходит через функцию активации:

Функция активации преобразует неограниченные значения входов в выход, имеющий ясную и предсказуемую форму. Одна из часто используемых функций активации – сигмоида:

Сигмоида

Сигмоида выдает результаты в интервале (0, 1). Можно представить, что она «упаковывает» интервал от минус бесконечности до плюс бесконечности в (0, 1): большие отрицательные числа превращаются в числа, близкие к 0, а большие положительные – к 1.

Простой пример

Допустим, наш двухвходовой нейрон использует сигмоидную функцию активации и имеет следующие параметры:

w=[0, 1] – это всего лишь запись w₁=0, w₂=1 в векторном виде. Теперь зададим нашему нейрону входные данные: x=[2, 3]. Мы используем скалярное произведение векторов, чтобы записать формулу в сжатом виде:

Наш нейрон выдал 0.999 при входах x=[2, 3]. Вот и все! Процесс передачи значений входов дальше, чтобы получить выход, называется прямой связью (feed forward).

Пишем код для нейрона

Настало время написать свой нейрон! Мы используем NumPy, популярную и мощную расчетную библиотеку для Python, которая поможет нам с вычислениями:

        import numpy as np

def sigmoid(x):
  # Наша функция активации: f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

class Neuron:
  def __init__(self, weights, bias):
    self.weights = weights
    self.bias = bias

  def feedforward(self, inputs):
    # Умножаем входы на веса, прибавляем порог, затем используем функцию активации
    total = np.dot(self.weights, inputs) + self.bias
    return sigmoid(total)

weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4                   # b = 4
n = Neuron(weights, bias)

x = np.array([2, 3])       # x1 = 2, x2 = 3
print(n.feedforward(x))    # 0.9990889488055994
    

Узнаете эти числа? Это тот самый пример, который мы только что рассчитали! И мы получили тот же результат – 0.999.

2. Собираем нейронную сеть из нейронов

Нейронная сеть – это всего лишь несколько нейронов, соединенных вместе. Вот как может выглядеть простая нейронная сеть:

У этой сети два входа, скрытый слой с двумя нейронами (h₁ и h₂) и выходной слой с одним нейроном (o₁). Обратите внимание, что входы для o₁ – это выходы из h₁ и h₂. Именно это создает из нейронов сеть.

Замечание

Скрытый слой – это любой слой между входным (первым) слоем сети и выходным (последним). Скрытых слоев может быть много!

Пример: прямая связь

Давайте используем сеть, изображенную выше, и будем считать, что все нейроны имеют одинаковые веса w=[0, 1], одинаковые пороговые значения b=0, и одинаковую функцию активации – сигмоиду. Пусть h₁, h₂ и o₁ обозначают выходные значения соответствующих нейронов.

Что получится, если мы подадим на вход x=[2, 3]?

Пишем свою нейросеть: пошаговое руководство

Отличный гайд про нейросеть от теории к практике. Вы узнаете из каких элементов состоит ИНС, как она работает и как ее создать самому.

Если вы в поисках пособия по искусственным нейронным сетям (ИНС), то, возможно, у вас уже имеются некоторые предположения относительно того, что это такое. Но знали ли вы, что нейронные сети — основа новой и интересной области глубинного обучения? Глубинное обучение — область машинного обучения, в наше время помогло сделать большой прорыв во многих областях, начиная с игры в Го и Покер с живыми игроками, и заканчивая беспилотными автомобилями. Но, прежде всего, глубинное обучение требует знаний о работе нейронных сетей.

В этой статье будут представлены некоторые понятия, а также немного кода и математики, с помощью которых вы сможете построить и понять простые нейронные сети. Для ознакомления с материалом нужно иметь базовые знания о матрицах и дифференциалах. Код будет написан на языке программирования Python с использованием библиотеки numpy. Вы построите ИНС, используя Python, которая с высокой точностью классифицировать числа на картинках.

Искусственные нейросеть (ИНС) — это программная реализация нейронных структур нашего мозга. Мы не будем обсуждать сложную биологию нашей головы, достаточно знать, что мозг содержит нейроны, которые являются своего рода органическими переключателями. Они могут изменять тип передаваемых сигналов в зависимости от электрических или химических сигналов, которые в них передаются. Нейросеть в человеческом мозге — огромная взаимосвязанная система нейронов, где сигнал, передаваемый одним нейроном, может передаваться в тысячи других нейронов. Обучение происходит через повторную активацию некоторых нейронных соединений. Из-за этого увеличивается вероятность вывода нужного результата при соответствующей входной информации (сигналах). Такой вид обучения использует обратную связь — при правильном результате нейронные связи, которые выводят его, становятся более плотными.

Искусственные нейронные сети имитируют поведение мозга в простом виде. Они могут быть обучены контролируемым и неконтролируемым путями. В контролируемой ИНС, сеть обучается путем передачи соответствующей входной информации и примеров исходной информации. Например, спам-фильтр в электронном почтовом ящике: входной информацией может быть список слов, которые обычно содержатся в спам-сообщениях, а исходной информацией — классификация для уведомления (спам, не спам). Такой вид обучения добавляет веса связям ИНС, но это будет рассмотрено позже.

Неконтролируемое обучение в ИНС пытается «заставить» ИНС «понять» структуру передаваемой входной информации «самостоятельно». Мы не будем рассматривать это в данном посте.

2.1 Искусственный нейрон

Биологический нейрон имитируется в ИНС через активационную функцию. В задачах классификации (например определение спам-сообщений) активационная функция должна иметь характеристику «включателя». Иными словами, если вход больше, чем некоторое значение, то выход должен изменять состояние, например с 0 на 1 или -1 на 1 Это имитирует «включение» биологического нейрона. В качестве активационной функции обычно используют сигмоидальную функцию:

Которая выглядит следующим образом:

import matplotlib.pylab as plt
import numpy as np
x = np.arange(-8, 8, 0.1)
f = 1 / (1 + np.exp(-x))
plt.plot(x, f)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()

Из графика можно увидеть, что функция «активационная» — она растет с 0 до 1 с каждым увеличением значения х. Сигмоидальная функция является гладкой и непрерывной. Это означает, что функция имеет производную, что в свою очередь является очень важным фактором для обучения алгоритма.

2.2 Узлы

Как было упомянуто ранее, биологические нейроны иерархически соединены в сети, где выход одних нейронов является входом для других нейронов. Мы можем представить такие сети в виде соединенных слоев с узлами. Каждый узел принимает взвешенный вход, активирует активационную функцию для суммы входов и генерирует выход.

Круг на картинке изображает узел. Узел является «местоположением» активационной функции, он принимает взвешенные входы, складывает их, а затем вводит их в активационную функцию. Вывод активационной функции представлен через h. Примечание: в некоторых источниках узел также называют перцептроном.

Что такое «вес»? По весу берутся числа (не бинарные), которые затем умножаются на входе и суммируются в узле. Иными словами, взвешенный вход в узел имеет вид:

где w_i— числовые значения веса ( b мы будем обсудим позже). Весы нам нужны, они являются значениями, которые будут меняться в течение процесса обучения. b является весом элемента смещения на 1, включение веса b делает узел гибким. Проще это понять на примере.

2.3 Смещение

Рассмотрим простой узел, в котором есть по одному входу и выходу:

Ввод для активационной функции в этом узле просто x₁w₁. На что влияет изменение в w₁ в этой простой сети?

w1 = 0.5
w2 = 1.0
w3 = 2.0
l1 = 'w = 0.5'
l2 = 'w = 1.0'
l3 = 'w = 2.0'
for w, l in [(w1, l1), (w2, l2), (w3, l3)]:
  f = 1 / (1 + np.exp(-x * w))
plt.plot(x, f, label = l)
plt.xlabel('x')
plt.ylabel('h_w(x)')
plt.legend(loc = 2)
plt.show()

Здесь мы можем видеть, что при изменении веса изменяется также уровень наклона графика активационной функции. Это полезно, если мы моделируем различные плотности взаимосвязей между входами и выходами. Но что делать, если мы хотим, чтобы выход изменялся только при х более 1? Для этого нам нужно смещение. Рассмотрим такую сеть со смещением на входе:

w = 5.0
b1 = -8.0
b2 = 0.0
b3 = 8.0
l1 = 'b = -8.0'
l2 = 'b = 0.0'
l3 = 'b = 8.0'
for b, l in [(b1, l1), (b2, l2), (b3, l3)]:
  f = 1 / (1 + np.exp(-(x * w + b)))
plt.plot(x, f, label = l)
plt.xlabel('x')
plt.ylabel('h_wb(x)')
plt.legend(loc = 2)
plt.show()

Из графика можно увидеть, что меняя «вес» смещения b, мы можем изменять время запуска узла. Смещение очень важно в случаях, когда нужно имитировать условные отношения.

2.4 Составленная структура

Выше было объяснено, как работает соответствующий узел / нейрон / перцептрон. Но, как вы знаете, в полной нейронной сети находится много таких взаимосвязанных между собой узлов. Структуры таких сетей могут принимать мириады различных форм, но самая распространенная состоит из входного слоя, скрытого слоя и выходного слоя. Пример такой структуры приведены ниже:

Ну рисунке выше можно увидеть три слоя сети — Слой 1 является входным слоем, где сеть принимает внешние входные данные. Слой 2 называют скрытым слоем, этот слой не является частью ни входа, ни выхода. Примечание: нейронные сети могут иметь несколько скрытых слоев, в данном примере для примера был показан лишь один. И наконец, Слой 3 является исходным слоем. Вы можете заметить, что между Шаром 1 (Ш1) и Шаром 2 (Ш2) существует много связей. Каждый узел в Ш1 имеет связь со всеми узлами в Ш2, при этом от каждого узла в Ш2 идет по одной связи к единому выходному узлу в Ш3. Каждая из этих связей должна иметь соответствующий вес.

2.5 Обозначение

Вся математика, приведенная выше, требует очень точной нотации. Нотация, которая используется здесь, используется и в руководстве по глубинному обучению от Стэнфордского Университета. В следующих уравнениях вес соответствующего связи будет обозначаться как w _ij^(l), где i — номер узла в слое l+1, а j- номер узла в слое l. Например, вес связи между узлом 1 в слое 1 и узлом 2 в слое 2 будет обозначаться как w ₂₁^(l). Непонятно, почему индексы 2-1 означают связь 1-2? Такая нотация более понятна, если добавить смещения.

Из графика выше видно, что смещение 1 связано со всеми узлами в соседнем слое. Смещение в Ш1 имеет связь со всеми узлами в Ш2. Так как смещение не является настоящим узлом с активационной функцией, оно не имеет и входов (его входное значение всегда равно константе). Вес связи между смещением и узлом будем обозначать через b_i^(l), где i- номер узла в слое l+1, так же, как в w _ij^(l). К примеру с w ₂₁^(l) вес между смещением в Ш1 и вторым узлом в Ш2 будет иметь обозначение b₂⁽¹⁾.

Помните, что эти значения -w _ij^(l)и b_i^(l) — будут меняться в течение процесса обучения ИНС.
Обозначение связи с исходным узлом будет выглядеть следующим образом: h_j^l, где j- номер узла в слое l. Тогда в предыдущем примере, связью с исходным узлом является h₁⁽²⁾.
Теперь давайте рассмотрим, как рассчитывать выход сети, когда нам известны вес и вход. Процесс нахождения выхода в нейронной сети называется процессом прямого распространения.

Чтобы продемонстрировать, как находить выход, имея уже известный вход, в нейронных сетях, начнем с предыдущего примера с тремя слоями. Ниже такая система представлена в виде системы уравнений:

, где f(∙) — активационная функция узла, в нашем случае сигмоидальная функция. В первой строке h₁⁽²⁾— выход первого узла во втором слое, его входами соответственно являются w₁₁⁽¹⁾x₁(1), w₁₂⁽¹⁾x₂(1),w₁₃⁽¹⁾x₃(1) и b₁⁽¹⁾. Эти входы было сложены, а затем переданы в активационную функцию для расчета выхода первого узла. С двумя следующими узлами аналогично.

Последняя строка рассчитывает выход единого узла в последнем третьем слое, он является конечной исходной точкой в нейронной сети. В нем вместо взвешенных входных переменных (x₁,x₂,x₃)берутся взвешенные выходы узлов с другой слоя (h₁⁽²⁾,h₂⁽²⁾,h₃⁽²⁾)и смещения. Такая система уравнений также хорошо показывает иерархическую структуру нейронной сети.

3.1 Пример прямого распространения

Приведем простой пример первого вывода нейронной сети языке Python . Обратите внимание, веса w₁₁⁽¹⁾,w₁₂⁽¹⁾,… между Ш1 и Ш2 идеально могут быть представлены в матрице:

Представим эту матрицу через массивы библиотеки numpy.

import numpy as np
w1 = np.array([
  [0.2, 0.2, 0.2],
  [0.4, 0.4, 0.4],
  [0.6, 0.6, 0.6]
])

Мы просто присвоили некоторые рандомные числовые значения весу каждой связи с Ш1. Аналогично можно сделать и с Ш2:

	w2 = np.zeros((1, 3))
	w2[0, : ] = np.array([0.5, 0.5, 0.5])

Мы можем присвоить некоторые значения весу смещения в Ш1 и Ш2:

b1 = np.array([0.8, 0.8, 0.8])
b2 = np.array([0.2])

Наконец, перед написанием основной программы для расчета выхода нейронной сети, напишем отдельную функцию для активационной функции:

	def f(x):
	  return 1 / (1 + np.exp(-x))

3.2 Первая попытка реализовать процесс прямого распространения

Приведем простой способ расчета выхода нейронной сети, используя вложенные циклы в Python. Позже мы быстро рассмотрим более эффективные способы.

def simple_looped_nn_calc(n_layers, x, w, b):
  for l in range(n_layers - 1): #Формируется входной массив - перемножения весов в каждом слое# Если первый слой, то входной массив равен вектору х# Если слой не первый, вход для текущего слоя равен# выходу предыдущего
if l == 0:
  node_in = x
else :
  node_in = h #формирует выходной массив для узлов в слое l + 1
h = np.zeros((w[l].shape[0], ))#проходит по строкам массива весов
for i in range(w[l].shape[0]): #считает сумму внутри активационной функции
f_sum = 0 #проходит по столбцам массива весов
for j in range(w[l].shape[1]):
  f_sum += w[l][i][j] * node_in[j] #добавляет смещение
f_sum += b[l][i]

#использует активационную функцию для расчета
#i - того выхода, в данном случае h2, h3, h4
h[i] = f(f_sum)
return h

Данная функция принимает в качестве входа номер слоя в нейронной сети, х — входной массив / вектор:

w = [w1, w2]
b = [b1, b2] #Рандомный входной вектор x
x = [1.5, 2.0, 3.0]

Функция сначала проверяет, чем является входной массив для соответствующего слоя с узлами / весами. Если рассматривается первый слой, то входом для второго слоя является входной массив xx, Умноженный на соответствующие веса. Если слой не первый, то входом для последующего будет выход предыдущего.
Вызов функции:

	simple_looped_nn_calc(3, x, w, b)

возвращает результат 0.8354. Можно проверить правильность, вставив те же значения в систему уравнений:

3.3 Более эффективная реализация

Использование циклов — не самый эффективный способ расчета прямого распространения на языке Python , потому что циклы в этом языке программирования работают довольно медленно. Мы кратко рассмотрим лучшие решения. Также можно будет сравнить работу алгоритмов, используя функцию в IPython:

	%timeit simple_looped_nn_calc(3, x, w, b)

В данном случае процесс прямого распространения с циклами занимает около 40 микросекунд. Это довольно быстро, но не для больших нейронных сетей с > 100 узлами на каждом слое, особенно при их обучении. Если мы запустим этот алгоритм на нейронной сети с четырьмя слоями, то получим результат 70 микросекунд. Эта разница является достаточно значительной.

3.4 Векторизация в нейронных сетях

Можно более компактно написать предыдущие уравнения, тем самым найти результат эффективнее. Сначала добавим еще одну переменную z_i^(l), которая является суммой входа в узел i слоя l, Включая смещение. Тогда для первого узла в Ш2, z будет равна:

, где n- количество узлов в Ш1. Используя это обозначение, систему уравнений можно сократить:

Обратите внимание на W, что означает матричную форму представления весов. Помните, что теперь все элементы в уравнении сверху являются матрицами / векторами. Но на этом упрощение не заканчивается. Данные уравнения можно свести к еще более краткому виду:

Так выглядит общая форма процесса прямого распространения, выход слоя l становится входом в слой l+1. Мы знаем, что h⁽¹⁾ является входным слоем x, а h^(nl)(где nl- номер слоя в сети) является исходным слоем. Мы также не стали использовать индексы i и j-за того, что можно просто перемножить матрицы — это даст нам тот же результат. Поэтому данный процесс и называется «векторизацией». Этот метод имеет ряд плюсов. Во-первых, код его реализации выглядит менее запутанным. Во-вторых, используются свойства по линейной алгебре вместо циклов, что делает работу программы быстрее. С numpy можно легко сделать такие подсчеты. В следующей части быстро повторим операции над матрицами, для тех, кто их немного подзабыл.

3.5 Умножение матриц

Распишем z^(l+1)=W^(l)h^(l)+b^(l) на выражение из матрицы и векторов входного слоя ( h^(l)=x):

Для тех, кто не знает или забыл, как перемножаются матрицы. Когда матрица весов умножается на вектор, каждый элемент в строке матрицы весов умножается на каждый элемент в столбце вектора, после этого все произведения суммируются и создается новый вектор (3х1). После перемножения матрицы на вектор, добавляются элементы из вектора смещения и получается конечный результат.

Каждая строка полученного вектора соответствует аргументу активационной функции в оригинальной НЕ матричной системе уравнений выше. Это означает, что в Python мы можем реализовать все, не используя медленные циклы. К счастью, библиотека numpy дает возможность сделать это достаточно быстро, благодаря функциям-операторам над матрицами. Рассмотрим код простой и быстрой версии функции simple_looped_nn_calc:

def matrix_feed_forward_calc(n_layers, x, w, b):
  for l in range(n_layers - 1):
  if l == 0:
  node_in = x
else :
  node_in = h
z = w[l].dot(node_in) + b[l]
h = f(z)
return h

Обратите внимание на строку 7, в которой происходит перемножение матрицы и вектора. Если вместо функции умножения a.dot (b) вы используете символ *, то получится нечто похожее на поэлементное умножение вместо настоящего произведения матриц.

Если сравнить время работы этой функции с предыдущей на простой сети с четырьмя слоями, то мы получим результат лишь на 24 микросекунды меньше. Но если увеличить количество узлов в каждом слое до 100-100-50-10, то мы получим гораздо большую разницу. Функция с циклами в этом случае дает результат 41 миллисекунду, когда у функции с векторизацией это занимает лишь 84 микросекунды. Также существуют еще более эффективные реализации операций над матрицами, которые используют пакеты глубинного обучения, такие как TensorFlow и Theano.

На этом все о процессе прямого распространения в нейронных сетях. В следующих разделах мы поговорим о способах обучения нейронных сетей, используя градиентный спуск и обратное распространение.

Расчеты значений весов, которые соединяют слои в сети, это как раз то, что мы называем обучением системы. В контролируемом обучении идея заключается в том, чтобы уменьшить погрешность между входом и нужным выходом. Если у нас есть нейросеть с одним выходным слоем и некоторой вход xx и мы хотим, чтобы на выходе было число 2, но сеть выдает 5, то нахождение погрешности выглядит как abs(2-5)=3. Говоря языком математики, мы нашли норму ошибки L¹(Это будет рассмотрено позже).

Смысл контролируемого обучения в том, что предоставляется много пар вход-выход уже известных данных и нужно менять значения весов, основываясь на этих примерах, чтобы значение ошибки стало минимальным. Эти пары входа-выхода обозначаются как (x⁽¹⁾,y⁽¹⁾),…,(x^(m),y^(m)), где m является количеством экземпляров для обучения. Каждое значение входа или выхода может представлять собой вектор значений, например x⁽¹⁾ не обязательно только одно значение, оно может содержать N-размерный набор значений. Предположим, что мы обучаем нейронную сеть выявлению спам-сообщений — в таком случае x⁽¹⁾ может представлять собой количество соответствующих слов, которые встречаются в сообщении:

y⁽¹⁾ в этом случае может представлять собой единое скалярное значение, например, 1 или 0, обозначающий, было сообщение спамом или нет. В других приложениях это также может быть вектор с K измерениями. Например, мы имеем вход xx, Который является вектором черно-белых пикселей, считанных с фотографии. При этом y может быть вектором с 26 элементами со значениями 1 или 0, обозначающие, какая буква была изображена на фото, например (1,0,…,0)для буквы а, (0,1,…,0) для буквы б и т. д.

В обучении сети, используя (x,y), целью является улучшение нахождения правильного y при известном x. Это делается через изменение значений весов, чтобы минимизировать погрешность. Как тогда менять их значение? Для этого нам и понадобится градиентный спуск. Рассмотрим следующий график:

На этом графике изображено погрешность, зависящую от скалярного значения веса, w. Минимально возможная погрешность обозначена черным крестиком, но мы не знаем какое именно значение w дает нам это минимальное значение. Подсчет начинается с рандомного значения переменной w, которая дает погрешность, обозначенную красной точкой под номером «1» на кривой. Нам нужно изменить w таким образом, чтобы достичь минимальной погрешности, черного крестика. Одним из самых распространенных способов является градиентный спуск.

Сначала находится градиент погрешности на «1» по отношению к w. Градиент является уровнем наклона кривой в соответствующей точке. Он изображен на графике в виде черных стрелок. Градиент также дает некоторую информацию о направлении — если он положителен при увеличении w, то в этом направлении погрешность будет увеличиваться, если отрицательный — уменьшаться (см. График). Как вы уже поняли, мы пытаемся сделать, чтобы погрешность с каждым шагом уменьшалась. Величина градиента показывает, как быстро кривая погрешности или функция меняется в соответствующей точке. Чем больше значение, тем быстрее меняется погрешность в соответствующей точке в зависимости от w.

Метод градиентного спуска использует градиент, чтобы принимать решение о следующей смены в w для того, чтобы достичь минимального значения кривой. Он итеративным методом, каждый раз обновляет значение w через:

, где w_н означает новое значение w, w_ст— текущее или «старое» значение w, ∇error является градиентом погрешности на w_ст и α является шагом. Шаг α также будет означать, как быстро ответ приближается к минимальной погрешности. При каждой итерации в таком алгоритме градиент должен уменьшаться. Из графика выше можно заметить, что с каждым шагом градиент «стихает». Как только ответ достигнет минимального значения, мы уходим из итеративного процесса. Выход можно реализовать способом условия «если погрешность меньше некоторого числа». Это число называют точностью.

4.1 Простой пример на коде

Рассмотрим пример простой имплементации градиентного спуска для нахождения минимума функции f(x)=x⁴-3x³+2 на языке Python . Градиент этой функции можно найти аналитически через производную f»(x)=4x³-9x². Это означает, что для любого xx мы можем найти градиент по этой простой формуле. Мы можем найти минимум через производную — x=2.25.

x_old = 0 # Нет разницы, какое значение, главное abs(x_new - x_old) > точность
x_new = 6 # Алгоритм начинается с x = 6
gamma = 0.01 # Размер шага
precision = 0.00001 # Точность

def df(x):
   y = 4 * x * * 3 - 9 * x * * 2
   return y

while abs(x_new - x_old) > precision:
   x_old = x_new
   x_new += -gamma * df(x_old)

print("Локальный минимум находится на %f"  % x_new)

Вывод этой функции: «Локальный минимум находится на 2.249965», что удовлетворяет правильному ответу с некоторой точностью. Этот код реализует алгоритм изменения веса, о котором рассказывалось выше, и может находить минимум функции с соответствующей точностью. Это был очень простой пример градиентного спуска, нахождение градиента при обучении нейронной сети выглядит несколько иначе, хотя и главная идея остается той же — мы находим градиент нейронной сети и меняем веса на каждом шагу, чтобы приблизиться к минимальной погрешности, которую мы пытаемся найти. Но в случае ИНС нам нужно будет реализовать градиентный спуск с многомерным вектором весов.

Мы будем находить градиент нейронной сети, используя достаточно популярный метод обратного распространения ошибки, о котором будет написано позже. Но сначала нам нужно рассмотреть функцию погрешности более детально.

4.2 Функция оценки

Существует более общий способ изобразить выражения, которые дают нам возможность уменьшить погрешность. Такое общее представление называется функция оценки. Например, функция оценки для пары вход-выход (x^z, y^z) в нейронной сети будет выглядеть следующим образом:

Выражение является функцией оценки учебного экземпляра z_th, где h^(nl)является выходом последнего слоя, то есть выход нейронной сети. h^(nl) можно представить как yпyп, Что означает полученный результат, когда нам известен вход xz. Две вертикальные линии означают норму L² погрешности или сумму квадратов ошибок. Сумма квадратов погрешностей является довольно распространенным способом представления погрешностей в системе машинного обучения. Вместо того, чтобы брать абсолютную погрешность abs(ypred(x^z)-y^z), мы берем квадрат погрешности. Мы не будем обсуждать причину этого в данной статье. 1/2 в начале просто константой, которая нормализует ответ после того, как мы продифференцируем функцию оценки во время обратного распространения.

Обратите внимание, что приведенная ранее функция оценки работает только с одной парой (x,y). Мы хотим минимизировать функцию оценки со всеми mm парами вход-выход:

Тогда как же мы будем использовать функцию J для обучения наших сетей? Конечно, используя градиентный спуск и обратное распространение ошибок. Сначала рассмотрим градиентный спуск в нейронных сетях более детально.

4.3 Градиентный спуск в нейронных сетях

Градиентный спуск для каждого веса w_(ij)^(l) и смещение bi(l) в нейронной сети выглядит следующим образом:

Выражение выше фактически аналогично представлению градиентного спуска:
w_new=w_old-α*∇error. Нет лишь некоторых обозначений, но достаточно понимать, что слева расположены новые значения, а справа — старые. Опять же задействован итерационный метод для расчета весов на каждой итерации, но на этот раз основываясь на функции оценки J(w,b).

Значения ∂/∂w_ij^(l)и ∂/∂b_i^(l) являются частными производными функции оценки, основываясь на значениях веса. Что это значит? Вспомните простой пример градиентного спуска ранее, каждый шаг зависит от наклона погрешности / оценки по отношению к весу. Производная также имеет значение наклона / градиента. Конечно, производная обозначается как d/dx. x в нашем случае является вектором, а это значит, что наша производная тоже будет вектором, который является градиент каждого измерения x.

4.4 Пример двумерного градиентного спуска

Рассмотрим пример стандартного двумерного градиентного спуска. Ниже представлены диаграмму работы двух итеративных двумерных градиентных спусков:

Синим обозначены контуры функции оценки, они обозначают области, в которых значение погрешности примерно одинаковы. Каждый шаг (p1→p2→p3) В градиентном спуске используют градиент или производную, которые обозначаются стрелкой / вектором. Этот вектор проходит через два пространства [x1, x2][x1,x2]и показывает направление, в котором находится минимум. Например, производная, исчисленная в p1 может быть d/dx=[2.1,0.7], Где производная является вектором с двумя значениями. Частичная производная ∂/∂x₁ в этом случае равна скаляру →[2.1]- иными словами, это значение градиента только в одном измерении поискового пространства (x1).

В нейронных сетях не существует простой полной функции оценки, с которой можно легко посчитать градиент, похожей на функцию, которую мы ранее рассматривали f(x)=x⁴-3x³+2). Мы можем сравнить выход нейронной сети с нашим ожидаемым значением y^(z), После чего функция оценки будет меняться из-за изменения в значениях веса, но как мы это сделаем со всеми скрытыми слоями в сети?

Поэтому нам нужен метод обратного распространения. Этот метод дает нам возможность «делить» функцию оценки или ошибку со всеми весами в сети. Другими словами, мы можем выяснить, как каждый вес влияет на погрешность.

4.5 Углубляемся в обратное распространение

Если математика вам не очень хорошо дается, то вы можете пропустить этот раздел. В следующем разделе вы узнаете, как реализовать обратное распространение языке программирования. Но если вы не против немного больше поговорить о математике, то продолжайте читать, вы получите более глубокие знания по обучению нейронных сетей.

Сначала, давайте вспомним базовые уравнения для нейронной сети с тремя слоями из предыдущих разделов:

Выход этой нейронной сети находится по формуле:

Мы можем упростить это уравнение к h₁(3)=f(z₁⁽²⁾), добавив новое значение z₁⁽²⁾, которое означает:

Предположим, что мы хотим узнать, как влияет изменение в весе w₁₂⁽²⁾ на функцию оценки. Это означает, что нам нужно вычислить ∂J/∂w₁₂⁽²⁾. Чтобы сделать это, нужно использовать правило дифференцирования сложной функции:

Если присмотреться, то правая часть полностью сокращается (по принципу 2552=22=1). ∂J∂w12(2) были разбиты на три множителя, два из которых можно прекрасно заменить. Начнем с ∂z₁⁽²⁾/∂w₁₂⁽²⁾:

Частичная производная z₁⁽²⁾ по w₁₂⁽²⁾ зависит только от одного произведения в скобках, w12(1)h3(2), Так как все элементы в скобках, кроме w₁₂⁽²⁾, не изменяются. Производная от константы всегда равна 1, а ∂/∂w₁₂⁽²⁾)сокращается до просто h₂⁽²⁾, Что является обычным выходом второго узла из слоя 2.

Следующая частичная производная сложной функции ∂h₁⁽³⁾/∂z₁⁽²⁾ является частичной производной активационной функции выходного узла h₁₍₃₎. Так что нам нужно брать производные активационной функции, следует условие ее включения в нейронные сети — функция должна быть дифференцированной. Для сигмоидальной активационной функции производная будет выглядеть так:

, где f(z)является самой активационной функцией. Теперь нам нужно разобраться, что делать с ∂J∂h₁⁽³⁾. Вспомните, что J(w,b,x,y) есть функция квадрата погрешности, выглядит так:

здесь y1 является ожидаемым выходом для выходного узла. Опять используем правило дифференцирования сложной функции:

Мы выяснили, как находить ∂J/∂w₁₂⁽²⁾по крайней мере для весов связей с исходным слоем. Перед тем, как перейти к одному из скрытых слоев, введем некоторые новые значения δ, чтобы немного сократить наши выражения:

, где i является номером узла в выходном слое. В нашем примере есть только один узел, поэтому i=1. Напишем полный вид производной функции оценки:

, где выходной слой, в нашем случае, l=2, а i соответствует номеру узла.

4.6 Распространение в скрытых слоях

Что делать с весами в скрытых слоях (в нашем случае в слое 2)? Для весов, которые соединены с выходным слоем, производная ∂J/∂h=-(y_i-h_i^(nl))имела смысл, т.к. функция оценки может быть сразу найдена через сравнение выходного слоя с существующими данными. Но выходы скрытых узлов не имеют подобных уже существующих данных для проверки, они связаны с функцией оценки только через другие слои узлов. Как мы можем найти изменения в функции оценки из-за изменений весов, которые находятся глубоко в нейронной сети? Как уже было сказано, мы используем метод обратного распространения.

Мы уже сделали тяжелую работу по правилу дифференцирования сложных функций, теперь рассмотрим все более графически. Значение, которое будет обратно распространяться, — δ_i^(nl), т.к. оно в ближайшей связи с функцией оценки. А что с узлом j во втором слое (скрытом слое)? Как он влияет на δ_i^(nl) в нашей сети? Он меняет другие значения из-за веса w_ij⁽²⁾(см. диаграмму ниже, где j=1 i=1).

Как можно понять из рисунка, выходной слой соединяется со скрытым узлом из-за веса. В случае, когда в исходном слое есть только один узел, общее выражение скрытого слоя будет выглядеть так:

, где j номер узла в слое l. Но что будет, если в исходном слое находится много выходных узлов? В этом случае δ_j^(l) находится по взвешенной сумме всех связанных между собой погрешностей, как показано на диаграмме ниже:

На рисунке показано, что каждое значение δ из исходного слоя суммируется для нахождения δ₁⁽²⁾, Но каждый выход δ должен быть взвешенным соответствующими значению w_i1⁽²⁾. Другими словами, узел 1 в слое 2 способствует изменениям погрешностей в трех выходных узлах, при этом полученная погрешность (или значение функции оценки) в каждом из этих узлов должна быть «передана назад» значению δ этого узла. Сформируем общее выражение значение δ для узлов в скрытом слое:
, где j является номером узла в слое l, i- номер узла в слое l+1(что аналогично обозначениям, которое мы использовали ранее). s_(l+1)— это количество узлов в слое l+1.
Теперь мы знаем, как находить:
Но что делать с весами смещения? Принцип работы с ними аналогичный обычным весам, используя правила дифференцирования сложных функций:

Отлично, теперь мы знаем, как реализовать градиентный спуск в нейронных сетях:

Однако, для такой реализации, нам нужно будет снова применить циклы. Как мы уже знаем из предыдущих разделов, циклы в языке программирования Python работают довольно медленно. Нам нужно будет понять, как можно векторизовать такие подсчеты.

4.7 Векторизация обратного распространения

Для того, чтобы понять, как векторизовать процесс градиентного спуска в нейронных сетях, рассмотрим сначала упрощенную векторизованную версию градиента функции оценки (внимание: это пока неправильная версия!):

Что представляет собой h^(l)? Все просто, вектор (s_l×1), где s_l является количеством узлов в слое l. Как тогда выглядит произведение h^(l)δ^(l+1)? Мы знаем, что α×∂J/∂W^(l) должно быть того же размера, что и матрица весов W(l), Мы также знаем, что результат h_(l)δ^(l+1) должен быть того же размера, что и матрица весов для слоя l. Иными словами, произведение должно быть размера (s_{l + 1}× s_l).

Мы знаем, что δ_(l+1) имеет размер (s_l+1×1), а h ^(l)— размер (s_l×1). По правилу умножения матриц, если матрицу (n×m)умножить на матрицу (o×p), То мы получим матрицу размера (n×p). Если мы просто перемножим h_(l) на δ_(l+1), то количество столбцов в первом векторе (один столбец) не будет равно количеству строк во втором векторе (3 строки). Поэтому, для того, чтобы можно было умножить эти матрицы и получить результат размера (s_l+1× s_l), Нужно сделать трансформирование. Оно меняет в матрице столбцы на строки и наоборот (например матрицу вида (s_l×1)на (1×s_l)). Трансформирование обозначается как буква T над матрицей. Мы можем сделать следующее:

Используя операцию трансформирования, мы можем достичь результата, который нам нужен.

Еще одно трансформирование нужно сделать с суммой погрешностей в обратном распространении:

символ (∙) в предыдущем выражении означает поэлементное умножение (произведение Адамара), не является умножением матриц. Обратите внимание, что произведение матриц (((W^(l))^Tδ_(l+1))требует еще одного сложения весов и значений δ.

4.8 Реализация этапа градиентного спуска

Как тогда интегрировать векторизацию в этапы градиентного спуска нашего алгоритма? Во-первых, вспомним полный вид нашей функции оценки, который нам нужно сократить:

Из формулы видно, что полная функция оценки состоит из суммы поэтапных расчетов функции оценки. Также следует вспомнить, как находится градиентный спуск (поэлементная и векторизованная версии):

Это означает, что по прохождению через экземпляры обучения нам нужно иметь отдельную переменную, которая равна сумме частных производных функции оценки каждого экземпляра. Такая переменная соберет в себе все значения для «глобального» подсчета. Назовем такую «суммированную» переменную ΔW^(l). Соответствующая переменная для смещения будет обозначаться как Δb^(l). Следовательно, при каждой итерации в процессе обучения сети нам нужно будет сделать следующие шаги:

Выполняя эти операции на каждой итерации, мы подсчитываем упомянутую ранее сумму Σ^m_{z= 1}∂/∂W^(l)J( w , b , x^(z), y^(z))(и аналогичная формула для b). После того, как будут проитерированы все экземпляры и получены все значения δ, мы обновляем значения параметров веса:

4.9 Конечный алгоритм градиентного спуска

И, наконец, мы пришли к определению метода обратного распространения через градиентный спуск для обучения наших нейронных сетей. Финальный алгоритм обратного распространения выглядит следующим образом:
Рандомная инициализация веса для каждого слоя W^(l). Когда итерация < границы итерации:

01. Зададим ΔW и Δb начальное значение ноль.
02. Для экземпляров от 1 до m: а. Запустите процесс прямого распространения через все n_l слоев. Храните вывод активационной функции в h^(l)б. Найдите значение δ^{( nl)} выходного слоя. Обновите ΔW^(l)и Δb^{( l )} для каждого слоя.
03. Запустите процесс градиентного спуска, используя:

Из этого алгоритма следует, что мы будем повторять градиентный спуск, пока функция оценки не достигнет минимума. На этом этапе нейросеть считается обученной и готовой к использованию.

Далее мы попробуем реализовать этот алгоритм на языке программирования для обучения нейронной сети распознаванию чисел, написанных от руки.

В предыдущем разделе мы рассмотрели теорию по обучению нейронной сети через градиентный спуск и метод обратного распространения. В этом разделе мы используем полученные знания на практике — напишем код, который прогнозирует, основываясь на данных MNIST. База данных MNIST — это набор примеров в нейронных сетях и глубинном обучении. Она включает в себя изображения цифр, написанных от руки, с соответствующими ярлыками, которые объясняют, что это за число. Каждое изображение размером 8х8 пикселей. В этом примере мы используем сети данных MNIST для библиотеки машинного обучения scikit learn в языке программирования Python . Пример такого изображения можно увидеть под кодом:

	from sklearn.datasets
	import load_digits
	digits = load_digits()
	print(digits.data.shape)
	import matplotlib.pyplot as plt
	plt.gray()
	plt.matshow(digits.images[1])
	plt.show()

Код, который мы собираемся написать в нашей нейронной сети, будет анализировать цифры, которые изображают пиксели на изображении. Для начала, нам нужно отсортировать входные данные. Для этого мы сделаем две следующие вещи:

01. Масштабировать данные.
02. Разделить данные на тесты и учебные тесты.

5.1 Масштабирование данных

Почему нам нужно масштабировать данные? Во-первых, рассмотрим представление пикселей одного из сетов данных:

digits.data[0, : ]
Out[2]:
   array([0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13.,
      15., 10., 15., 5., 0., 0., 3., 15., 2., 0., 11.,
      8., 0., 0., 4., 12., 0., 0., 8., 8., 0., 0.,
      5., 8., 0., 0., 9., 8., 0., 0., 4., 11., 0.,
      1., 12., 7., 0., 0., 2., 14., 5., 10., 12., 0.,
      0., 0., 0., 6., 13., 10., 0., 0., 0.
   ])

Заметили ли вы, что входные данные меняются в интервале от 0 до 15? Достаточно распространенной практикой является масштабирование входных данных так, чтобы они были только в интервале от [0, 1], или [1, 1]. Это делается для более легкого сравнения различных типов данных в нейронной сети. Масштабирование данных можно легко сделать через библиотеку машинного обучения scikit learn:

from sklearn.preprocessing import StandardScaler
X_scale = StandardScaler()
X = X_scale.fit_transform(digits.data)
X[0,:]
Out[3]:
array([ 0.        , -0.33501649, -0.04308102,  0.27407152, -0.66447751,
       -0.84412939, -0.40972392, -0.12502292, -0.05907756, -0.62400926,
        0.4829745 ,  0.75962245, -0.05842586,  1.12772113,  0.87958306,
       -0.13043338, -0.04462507,  0.11144272,  0.89588044, -0.86066632,
       -1.14964846,  0.51547187,  1.90596347, -0.11422184, -0.03337973,
        0.48648928,  0.46988512, -1.49990136, -1.61406277,  0.07639777,
        1.54181413, -0.04723238,  0.        ,  0.76465553,  0.05263019,
       -1.44763006, -1.73666443,  0.04361588,  1.43955804,  0.        ,
       -0.06134367,  0.8105536 ,  0.63011714, -1.12245711, -1.06623158,
        0.66096475,  0.81845076, -0.08874162, -0.03543326,  0.74211893,
        1.15065212, -0.86867056,  0.11012973,  0.53761116, -0.75743581,
       -0.20978513, -0.02359646, -0.29908135,  0.08671869,  0.20829258,
       -0.36677122, -1.14664746, -0.5056698 , -0.19600752])

Стандартный инструмент масштабирования в scikit learn нормализует данные через вычитание и деление. Вы можете видеть, что теперь все данные находятся в интервале от -2 до 2. По же на счет выходных данных yy, то обычно нет необходимости их масштабировать.

5.2 Создание тестов и учебных наборов данных

В машинном обучении появляется такой феномен, который называется «переобучением». Это происходит, когда модели, во время учебы, становятся слишком запутанными — они достаточно хорошо обучены, но когда им передаются новые данные, которые они никогда на «видели», то результат, который они выдают, становится плохим. Иными словами, модели генерируются не очень хорошо. Чтобы убедиться, что мы не создаем слишком сложные модели, обычно набор данных разбивают на учебные наборы и тестовые наборы. Учебный набором данных, на которых модель будет учиться, а тестовый набор — это данные, на которых модель будет тестироваться после завершения обучения. Количество учебных данных должно быть всегда больше тестовых данных. Обычно они занимают 60-80% от набора данных.

Опять же, scikit learn легко разбивает данные на учебные и тестовые наборы:

from sklearn.model_selection import train_test_split
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)

В этом случае мы выделили 40% данных на тестовые наборы и 60% соответственно на обучение. Функция train_test_split в scikit learn добавляет данные рандомно в различные базы данных — то есть, функция не берет первые 60% строк для учебного набора, а то, что осталось, использует как тестовый.

5.3 Настройка выходного слоя

Для того, чтобы получать результат — числа от 0 до 9, нам нужен выходной слой. Более-менее точная нейросеть, как правило, имеет выходной слой с 10 узлами, каждый из которых выдает число от 0 до 9. Мы хотим научить сеть так, чтобы, например, при цифре 5 на изображении, узел с цифрой 5 в исходном слое имел наибольшее значение. В идеале, мы бы хотели иметь следующий вывод: [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]. Но на самом деле мы можем получить что-то похожее на это: [0.01, 0.1, 0.2, 0.05, 0.3, 0.8, 0.4, 0.03, 0.25, 0.02]. В таком случае мы можем взять крупнейших индекс в исходном массиве и считать это нашим полученным числом.

В данных MNIST нужны результаты от изображений записаны как отдельное число. Нам нужно конвертировать это единственное число в вектор, чтобы его можно было сравнивать с исходным слоем с 10 узлами. Иными словами, если результат в MNIST обозначается как «1», то нам нужно его конвертировать в вектор: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]. Такую конвертацию осуществляет следующий код:

import numpy as np
def convert_y_to_vect(y):
    y_vect = np.zeros((len(y), 10))
    for i in range(len(y)):
        y_vect[i, y[i]] = 1
    return y_vect

y_v_train = convert_y_to_vect(y_train)
y_v_test = convert_y_to_vect(y_test)
y_train[0], y_v_train[0]
Out[8]:
(1, array([ 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]))

Этот код конвертирует «1» в вектор [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].

5.4 Создаем нейросеть

Следующим шагом является создание структуры нейронной сети. Для входного слоя, мы знаем, что нам нужно 64 узла, чтобы покрыть 64 пикселей изображения. Как было сказано ранее, нам нужен выходной слой с 10 узлами. Нам также потребуется скрытый слой в нашей сети. Обычно, количество узлов в скрытых слоях не менее и не больше количества узлов во входном и выходном слоях. Объявим простой список на языке Python , который определяет структуру нашей сети:

nn_structure = [64, 30, 10]

Мы снова используем сигмоидальную активационную функцию, так что сначала нужно объявить эту функцию и ее производную:

def f(x):
    return 1 / (1 + np.exp(-x))

def f_deriv(x):
    return f(x) * (1 - f(x))

Сейчас мы не имеем никакого представления, как выглядит наша нейросеть. Как мы будем ее учить? Вспомним наш алгоритм из предыдущих разделов:
Рандомно инициализируем веса для каждого слоя W^(l) Когда итерация <границы итерации:

01. Зададим ΔW и Δb начальное значение ноль.
02. Для экземпляров от 1 до m: а. Запустите процесс прямого распространения через все n_l слоев. Храните вывод активационной функции в h^(l)б. Найдите значение δ^{( nl)} выходного слоя. Обновите ΔW^(l)и Δb^{( l )} для каждого слоя.
03. Запустите процесс градиентного спуска, используя:

Значит первым этапом является инициализация весов для каждого слоя. Для этого мы используем словари в языке программирования Python (обозначается через {}). Рандомные значения предоставляются весам для того, чтобы убедиться, что нейросеть будет работать правильно во время обучения. Для рандомизации мы используем random_sample из библиотеки numpy. Код выглядит следующим образом:

import numpy.random as r
def setup_and_init_weights(nn_structure):
    W = {}
    b = {}
    for l in range(1, len(nn_structure)):
        W[l] = r.random_sample((nn_structure[l], nn_structure[l-1]))
        b[l] = r.random_sample((nn_structure[l],))
    return W, b

Следующим шагом является присвоение двум переменным ΔW и Δb нулевых начальных значений (они должны иметь такой же размер, что и матрицы весов и смещений)

def init_tri_values(nn_structure):
    tri_W = {}
    tri_b = {}
    for l in range(1, len(nn_structure)):
        tri_W[l] = np.zeros((nn_structure[l], nn_structure[l-1]))
        tri_b[l] = np.zeros((nn_structure[l],))
    return tri_W, tri_b

Далее запустим процесс прямого распространения через нейронную сеть:

def feed_forward(x, W, b):
    h = {1: x}
    z = {}
    for l in range(1, len(W) + 1):
    #Если первый слой, то весами является x, в противном случае
    #Это выход из последнего слоя
 if l == 1:
            node_in = x
        else:
            node_in = h[l]
        z[l+1] = W[l].(l+1)
                    tri_b[l] += delta[l+1]
        # запускает градиентный спуск для весов в каждом слое
        for l in range(len(nn_structure) - 1, 0, -1):
            W[l] += -alpha * (1.0/m * tri_W[l])
            b[l] += -alpha * (1.0/m * tri_b[l])
        # завершает расчеты общей оценки
        avg_cost = 1.0/m * avg_cost
        avg_cost_func.append(avg_cost)
        cnt += 1
    return W, b, avg_cost_func

Функция сверху должна быть немного объяснена. Во-первых, мы не задаем лимит работы градиентного спуска, основываясь на изменениях или точности функции оценки. Вместо этого, мы просто запускаем её с фиксированным числом итераций (3000 в нашем случае), а затем наблюдаем, как меняется общая функция оценки с прогрессом в обучении. В каждой итерации градиентного спуска, мы перебираем каждый учебный экземпляр (range (len (y)) и запускаем процесс прямого распространения, а после него и обратное распространение. Этап обратного распространения является итерацией через слои, начиная с выходного слоя к началу — range (len (nn_structure), 0, 1). Мы находим среднюю оценку на исходном слое (l == len (nn_structure)). Мы также обновляем значение ΔW и Δb с пометкой tri_W и tri_b, для каждого слоя, кроме исходного (исходный слой не имеет никакого связи, который связывает его со следующим слоем).

И наконец, после того, как мы прошлись по всем учебным экземплярам, накапливая значение tri_W и tri_b, мы запускаем градиентный спуск и меняем значения весов и смещений:

После окончания процесса, мы возвращаем полученные вес и смещение со средней оценкой для каждой итерации. Теперь время вызвать функцию. Ее работа может занять несколько минут, в зависимости от компьютера.

W, b, avg_cost_func = train_nn(nn_structure, X_train, y_v_train)

Мы можем увидеть, как функция средней оценки уменьшилась после итерационной работы градиентного спуска:

plt.plot(avg_cost_func)
plt.ylabel('Средняя J')
plt.xlabel('Количество итераций')
plt.show()

Выше изображен график, где показано, как за 3000 итераций нашего градиентного спуска функция средней оценки снизилась и маловероятно, что подобная итерация изменит результат.

5.5 Оценка точности модели

Теперь, после того, как мы научили нашу нейросеть MNIST, мы хотим увидеть, как хорошо она работает на тестах. Дан входной тест (64 пикселя), нам нужно получить вывод нейронной сети — это делается через запуск процесса прямого распространения через сеть, используя наши полученные значения веса и смещения. Как было сказано ранее, мы выбираем результат выходного слоя через выбор узла с максимальным выводом. Для этого можно использовать функцию numpy.argmax, она возвращает индекс элемента массива с наибольшим значением:

def predict_y(W, b, X, n_layers):
    m = X.shape[0]
    y = np.zeros((m,))
    for i in range(m):
        h, z = feed_forward(X[i, :], W, b)
        y[i] = np.argmax(h[n_layers])
    return y

Теперь, наконец, мы можем оценить точность результата (процент раз, когда сеть выдала правильный результат), используя функцию accuracy_score из библиотеки scikit learn:

from sklearn.metrics import accuracy_score
y_pred = predict_y(W, b, X_test, 3)
accuracy_score(y_test, y_pred)*100

Мы получили результат 86% точности. Звучит довольно неплохо? На самом деле, нет, это довольно низкая точностью. В наше время точность алгоритмов глубинного обучения достигает 99.7%, мы немного отстали.

10 крутых примеров из недавних новостей

Мы погуляли по телеграм-каналам и насобирали кучу всего интересного о нейросетях. Вот наши основные источники:

• @denissexy Denis Sexy IT: «О нейронных сетях, виртуальной реальности и технологиях – простым языком»
• @brodetsky Технологии, медиа и общество
• @pathetic_low_freq Жалкие низкочастотники: «персональный канал безумных ссылок. Ожидаются: безумные картинки, странная математика, нёрдовский юмор»
• @NeuralShit «Проклятые нейронные сети»
• @mustreads «Рациональность, трансгуманизм, книги и статьи»
• @CGIT_Vines «Канал о сферах CG, Игр и Нейроcетей, всё с помощью чего мы генерируем визуальное и интерактивное искусство»
• @addmeto

Под каждым примером дали ссылку на источник.

«Удаление» человека с видеоизображения в режиме реального времени

Вы помните, как в кино на камеры подавали статическое изображение, чтобы не было видно злоумышленников? Так вот, им даже не снилось, что когда-то можно будет просто вставить в код камеры алгоритм, который стирает вас с видео, все остальное будет реальным.

Редкий случай, когда до такого не додумались даже в фантастических фильмах. Обратите внимание, система работает прямо в браузере, на клиентской стороне.

Интересно? Проект открытый, вот GithHub-репозиторий автора.

Источник

Поиск людей, похожих на художественный портрет

Что будет, если дать немного модернизированной нейронке StyleGAN2 на вход лицо с классической картины и попросить сгенерировать лица людей, которые по мнению нейронки максимально подходят под эти картины?

Получится что-то вроде такого, как ниже.

Код выложен здесь.

Источник

Шахматная партия с программой, пишущей тексты

Недавно была сыграна удивительная шахматная партия. Играла компьютерная программа против человека. Но удивителен не результат партии (шахматные программы сегодня легко обыгрывают даже чемпионов мира, хотя в этот раз победил человек), а то, что это была за программа. Это GPT-2, нейросеть, которая продолжает за тебя написанный текст.

GPT-2 успешно сопротивлялась в партии против человека … даже не зная о том, что играет в шахматы. Нейроcети дали тексты шахматной нотации (записи ходов латиницей, т.е. e2-e4 и т.д.) – базу из нескольких миллионов сыгранных шахматных партий. При этом программу не учили правилам шахмат, для неё все эти записи партий были просто текстом.

Вот инструкция для тех, кто хочет тоже сыграть партию с GPT.

Источник

«Пересадка» лиц актёров

DeepFake-ролики становятся всё более правдоподобными – вот, например, Роберт Дауни младший и Том Холланд в «Назад в будущее».

Можете потом сказать внукам, что это вырезанная сцена из «Мстителей: Финал». Но лучше, конечно, покажите оригинал.

Источник

Если хотите сами попробовать сделать DeepFake, вот туториал.

Один из главных популяризаторов Deepfake – Hao Li, у него миллион разных регалий, в том числе он сыграл ключевую роль в появлении анимоджи на IphoneX, бывший научный руководитель ILM и много чего еще.

На этом видео он тизерит своё приложение Pinscreen и алгоритмы, используемые в нем, в контексте вреда Deepfake для человечества на всемирном экономическом форуме в Давосе.

Источник

Массовое распространение дезинформации

Пример не из радостных, но хорошо, что такое пока умеют распознавать.

Facebook отчитался, что заблокировал 610 FB аккаунтов, 89 страниц, 156 групп (с названиями вроде «America Needs President Trump, TRUMP MAGA 2020, WE STAND WITH TRUMP & PENCE!») и 72 Instagram аккаунта из единого ботнета, у всех у них были аватарки, сгенерированные нейронной сетью. Владельцы ботнета потратили 9 миллионов долларов на рекламу «За-Трамповых взглядов» и «Анти-китайской пропаганды».

В Facebook сказали, что вычислили их по «фону», потому что на нем видны артефакты и следы алгоритмического шума. Вопрос времени, когда фон станет нормальным и придется искать новые способы выявления таких фотографий.

Источник

Колоризация фотографий

С каждым годом качество колоризации становится лучше, на фото ниже новая версия алгоритма DeOldify, пока не выложенная в паблик, но которая уже сейчас выглядит лучше, чем все, что было до этого.

Вы можете скинуть автору алгоритма ЧБ фото, и он вышлет вам, что получилось, кроме того можно посмотреть другие примеры:

Ждем релиза ✨

Источник

Оптимизация поиска новых лекарств

Проблема современной фармакологии в том, что для разработки новых лекарств приходится создавать и тестировать очень сложные молекулы. Молекулы могут иметь много разных параметров.

Чтобы синтезировать и протестировать все потенциально эффективные формулы, фармацевтам элементарно не хватает времени и ресурсов. Цикл создания нового лекарственного препарата может составлять до пяти лет. Но вот это моделирование разных молекул и прогнозирование свойств вещества исходя из устройства молекулы – отличная задача для искусственного интеллекта.

Так вот, британский стартап совместно с японской фармацевтической компанией нашёл с помощью ИИ формулу потенциально нового средства от обсессивно-компульсивного расстройства. Скоро в Японии пройдёт первый этап его клинического тестирования.

Вы могли видеть об этом заголовки вроде «ИИ создал новое лекарство», но всё немного сложнее. Новое вещество может стать лекарством только после нескольких этапов клинических испытаний – оно должно оказаться эффективным, не токсичным и так далее.

То, что удалось сделать с помощью ИИ – по сути, дотестовая оптимизация, то есть лишь начальный этап разработки лекарства. Без ИИ формулы таких лекарств подбирают 2-3 года. Здесь же ИИ справился с перебором разных комбинаций и параметров молекулы всего за год.

В общем, всё как в большинстве новостей про ИИ – машины пока не дают таких фантастических результатов, как хотелось бы (т.е. до «нажали кнопку – получили новое лекарство» ещё очень далеко), но позволяют заметно оптимизировать рутинные процессы.

Источник

Создание анимаций с большими значениями FPS

Следующий пример искусственного интеллекта позволяет создавать новые кадры в видео и анимациях, делая движение объектов более гладким.

Вот пример с Чебурашкой. Чтобы почувствовать более гладкое движение, нужно поставить на YouTube 720p50.

Распознавание дорожных знаков для ограничения скорости автомобиля

В автомобилях Tesla есть опция Speed Assist – камера распознаёт дорожные знаки с ограничением скорости и передаёт данные системе круиз-контроля. Удобная фича – водителю не надо лишний раз обращать внимание на дорожные знаки, машина сама их видит и разгоняется только до разрешенной скорости.

Но в лаборатории McAfee нашли занятный баг – наклеив на дорожный знак всего одну наклейку, систему распознавания можно обмануть и заставить машину разгоняться до 85 миль в час вместо 35. Баг не работает в новых моделях Driver Assistant, но много машин используют старую версию. Побыстрее бы его пофиксили, а то ведь такую наклейку могут наклеить на знак не только исследователи в рамках эксперимента.

Источник

Оценка привлекательности

Есть такой краудсорсинговый сервис Photofeeler для отбора фотографий (для резюме, тиндера и т.п.), куда можно загрузить свою фотографию и получить оценок по разным шкалам (ум, привлекательность, благонадежность) от сообщества – это условно бесплатно, но чтобы получить оценки, надо самому оценить сколько-то чужих фотографий.

Так вот они подсобрали данных и обучили на них сетку Photofeeler-D3, неплохо предсказывающую человеческие оценки, в т. ч. по видеопотоку. Выше – пример видео из поста, где автор кривляется перед камерой, а сетка оценивает результат в реальном времени. Очки добавляют ума, но крадут привлекательность 😉

Источник

Бонус: пара ссылок позалипать

***

Думаете, что уж вас-то нейросети не обманут? Держите ссылку на наш клевый тест об успехах ИИ.

Если знаете ещё классные примеры, скидывайте в комментарии.

Хотите узнать больше – подписывайтесь на вышеперечисленные каналы и читайте наши статьи:

У нас тоже есть канал в телеграм (@proglibrary), учитесь вместе с нами.

7 шалостей с нейросетями: алгоритмы ищут пьяных, гоняют котов, сочиняют песни

Интригующие заголовки, речи «под Обаму» и машинный «Гарри Поттер»

Норвежский программист Ларс Эйднес решил добавить компьютеру творческую искру. Для начала он научил нейронную сеть писать броские интернет-заголовки в духе «Семь секретов долголетия, о которых молчат тибетские ламы». Для этого он загрузил примерно 2 млн примеров с сайтов — корифеев жанра: BuzzFeed, Gawker, Jezebel, The Huffington Post и Upworthy. После тренировки сеть стала выдавать заголовки, в большинстве из которых была верная грамматика, а кое-где даже мелькал смысл. Потом Эйднес запустил целый новостной сайт, целиком написанный нейронными сетями. Новые заметки на нем выходят раз в 20 минут, а главная страница формируется исходя из просмотров статей и голосов читателей. Сегодня Click-o-Tron передает, что Джеймс Кэмерон защищает возможные проблемы с геями, Майли Сайрус исполнилось 13 лет, и вдобавок предлагает почитать о 16 самых подходящих городах для ресторана на кухне.

Что-то подобное проделал и журналист технологического сайта Engadget Аарон Суппурис. Он запрограммировал бота на основе той же нейронной сети, что была у Эйднеса, и загрузил туда тексты Engadget. К третьей версии бот научился копировать стилистику авторов сайта и выдавал более-менее вразумительные заметки. Правда, Суппурис полагает, что без чудесных инноваций нейронные сети никогда не заменят живого журналиста, зато пригодятся как удобный вспомогательный инструмент.

Другие экспериментаторы задавались еще более неординарными целями. Один научил нейронную сеть писать речи в стиле Барака Обамы — та неизменно желала божьего благословления. Другой загрузил книги о Гарри Поттере и получил новый том приключений юного волшебника. Третий натренировал сеть на любовных романах и строчках из песен Тейлор Свифт, чтобы компьютер подобающе описывал изображения на картинках. Исследователи Google тоже прогнали через сеть пикантное чтиво, чтобы та научилась писать в подобном стиле. Правда, сделали они это не ради забавы, а для дела: низкопробная беллетристика должна очеловечить язык голосового помощника и почтового клиента.

Учебное пособие по рекуррентным нейронным сетям

, часть 1 — Введение в RNN — WildML

Рекуррентные нейронные сети (RNN) — популярные модели, которые показали большие перспективы во многих задачах НЛП. Но, несмотря на их недавнюю популярность, я нашел лишь ограниченное количество ресурсов, которые подробно объясняют, как работают RNN и как их реализовать. Вот о чем этот урок. Это серия из нескольких частей, в которой я планирую рассказать следующее:

1. Введение в RNN (этот пост)
2. Реализация RNN с использованием Python и Theano
3. Понимание алгоритма обратного распространения во времени (BPTT) и проблемы исчезающего градиента
4. Внедрение GRU / LSTM RNN

В рамках учебного курса мы реализуем языковую модель на основе повторяющейся нейронной сети.Языковые модели применяются двояко: во-первых, они позволяют нам оценивать произвольные предложения в зависимости от вероятности их появления в реальном мире. Это дает нам некоторую степень грамматической и семантической правильности. Такие модели обычно используются как часть систем машинного перевода. Во-вторых, языковая модель позволяет нам генерировать новый текст (я думаю, что это гораздо более крутое приложение). Обучение языковой модели на основе Шекспира позволяет нам создавать текст, подобный Шекспиру. Этот забавный пост Андрея Карпати демонстрирует, на что способны символьные языковые модели, основанные на RNN.

Я предполагаю, что вы немного знакомы с основными нейронными сетями. Если вы этого не сделаете, вы можете перейти к разделу «Реализация нейронной сети с нуля», в котором представлены идеи и реализация, лежащие в основе разовых сетей.

Что такое RNN?

Идея RNN заключается в использовании последовательной информации. В традиционной нейронной сети мы предполагаем, что все входы (и выходы) независимы друг от друга. Но для многих задач это очень плохая идея.Если вы хотите предсказать следующее слово в предложении, вам лучше знать, какие слова были перед ним. RNN называются рекуррентными , потому что они выполняют одну и ту же задачу для каждого элемента последовательности, а результат зависит от предыдущих вычислений. Еще один способ думать о RNN — это то, что у них есть «память», которая фиксирует информацию о том, что было вычислено на данный момент. Теоретически RNN могут использовать информацию в произвольно длинных последовательностях, но на практике они ограничиваются просмотром только нескольких шагов (подробнее об этом позже).Вот как выглядит типичная RNN:

Рекуррентная нейронная сеть и развертывание во времени вычислений, участвующих в ее прямом вычислении. Источник: Nature

На приведенной выше диаграмме показано, что RNN развернута, (или развернута) в полную сеть. Под развертыванием мы просто подразумеваем, что мы записываем сеть для полной последовательности. Например, если интересующая нас последовательность представляет собой предложение из 5 слов, сеть будет развернута в 5-слойную нейронную сеть, по одному слою для каждого слова.Формулы, управляющие вычислениями в RNN, следующие:

Здесь следует отметить несколько моментов:

Что могут делать RNN?

RNN показали большой успех во многих задачах НЛП. Здесь я должен упомянуть, что наиболее часто используемый тип RNN — это LSTM, которые намного лучше фиксируют долгосрочные зависимости, чем обычные RNN. Но не волнуйтесь, LSTM — это, по сути, то же самое, что и RNN, которую мы будем развивать в этом руководстве, просто у них есть другой способ вычисления скрытого состояния.Мы рассмотрим LSTM более подробно в одной из следующих публикаций. Вот несколько примеров применения RNN в NLP (это не исчерпывающий список).

Моделирование языка и создание текста

Учитывая последовательность слов, мы хотим предсказать вероятность каждого слова с учетом предыдущих слов. Языковые модели позволяют нам измерить вероятность предложения, что является важным входом для машинного перевода (поскольку предложения с высокой вероятностью обычно являются правильными). Побочным эффектом возможности предсказать следующее слово является то, что мы получаем генеративную модель , которая позволяет нам генерировать новый текст путем выборки из выходных вероятностей.И в зависимости от того, какие у нас обучающие данные, мы можем генерировать всевозможные вещи. В языковом моделировании наш ввод обычно представляет собой последовательность слов (например, закодированных как горячие векторы), а наш вывод — это последовательность предсказанных слов. При обучении сети мы устанавливаем, так как мы хотим, чтобы вывод на этапе был фактическим следующим словом.

Научные статьи о языковом моделировании и создании текста:

Машинный перевод

Машинный перевод

похож на языковое моделирование в том, что мы вводим последовательность слов на исходном языке (например,грамм. Немецкий). Мы хотим вывести последовательность слов на нашем целевом языке (например, английском). Ключевое отличие заключается в том, что наш вывод начинается только после того, как мы увидели весь ввод, потому что первое слово наших переведенных предложений может потребовать информации, полученной из полной входной последовательности.

RNN для машинного перевода. Источник изображения: http://cs224d.stanford.edu/lectures/CS224d-Lecture8.pdf

Исследовательские статьи о машинном переводе:

Распознавание речи

Учитывая входную последовательность акустических сигналов от звуковой волны, мы можем предсказать последовательность фонетических сегментов вместе с их вероятностями.

Исследовательские работы по распознаванию речи:

Создание описаний изображений

Вместе со сверточными нейронными сетями, RNN использовались как часть модели для генерации описаний немаркированных изображений. Удивительно, насколько хорошо это работает. Комбинированная модель даже выравнивает сгенерированные слова с функциями, найденными на изображениях.

Глубокие визуально-семантические согласования для создания описаний изображений. Источник: http://cs.stanford.edu/people/karpathy/deepimagesent/

Учебные RNN

Обучение RNN аналогично обучению традиционной нейронной сети.Мы также используем алгоритм обратного распространения ошибки, но с небольшим изменением. Поскольку параметры являются общими для всех временных шагов в сети, градиент на каждом выходе зависит не только от вычислений текущего временного шага, но и от предыдущих временных шагов. Например, чтобы вычислить градиент при, нам нужно будет выполнить 3 шага обратного распространения и суммировать градиенты. Это называется обратным распространением во времени (BPTT). Если в этом нет особого смысла, не волнуйтесь, у нас будет целая статья о кровавых подробностях.На данный момент просто имейте в виду тот факт, что обычные RNN, обученные с помощью BPTT, испытывают трудности с изучением долгосрочных зависимостей (например, зависимостей между шагами, которые находятся далеко друг от друга) из-за того, что называется проблемой исчезающего / взрывающегося градиента. Существует некоторый механизм для решения этих проблем, и определенные типы RNN (например, LSTM) были специально разработаны для их решения.

Расширения RNN

За прошедшие годы исследователи разработали более сложные типы RNN, чтобы устранить некоторые недостатки ванильной модели RNN.Мы рассмотрим их более подробно в одном из следующих постов, но я хочу, чтобы этот раздел служил кратким обзором, чтобы вы были знакомы с таксономией моделей.

Двунаправленные RNN основаны на идее, что выходной сигнал во времени может зависеть не только от предыдущих элементов в последовательности, но и от будущих элементов. Например, чтобы предсказать пропущенное слово в последовательности, вы хотите посмотреть и на левый, и на правый контекст. Двунаправленные RNN довольно просты. Это всего лишь две RNN, поставленные друг на друга.Выходные данные затем вычисляются на основе скрытого состояния обеих RNN.

Глубокие (двунаправленные) RNN похожи на двунаправленные RNN, только теперь у нас есть несколько уровней на каждый временной шаг. На практике это дает нам более высокую способность к обучению (но нам также нужно много данных для обучения).

Сети LSTM сейчас довольно популярны, о них мы кратко говорили выше. LSTM не имеют принципиально отличной архитектуры от RNN, но они используют другую функцию для вычисления скрытого состояния.Память в LSTM называется ячейками , и вы можете думать о них как о черных ящиках, которые принимают в качестве входных данных предыдущее состояние и текущий ввод. Эти клетки внутренне решают, что оставить (а что стереть) в памяти. Затем они объединяют предыдущее состояние, текущую память и ввод. Оказывается, эти типы модулей очень эффективны при фиксации долгосрочных зависимостей. Поначалу LSTM могут сбивать с толку, но если вы хотите узнать больше, у этого поста есть отличное объяснение.

Заключение

Пока все хорошо. Надеюсь, вы получили общее представление о том, что такое RNN и на что они способны. В следующем посте мы реализуем первую версию нашей языковой модели RNN с использованием Python и Theano. Пожалуйста, оставляйте вопросы в комментариях!

Проектирование нейронной сети

Проектирование нейронной сети

Дизайн нейронной сети (2-е издание)

Мартин Т. Хаган, Ховард Б. Демут, Марк Х. Бил, Орландо Де
Джесс

ISBN-10 : 0-9717321-1-6

ISBN-13 :
978-0-9717321-1-7

NEURAL NETWORK DESIGN (2-е издание) предоставляет четкий и подробный обзор
фундаментальных архитектур нейронных сетей и правил обучения.В нем
авторы подчеркивают фундаментальное понимание основных нейронных
сети и методы их обучения. Авторы также обсуждают
приложения сетей к практическим инженерным задачам в шаблоне
системы распознавания, кластеризации, обработки сигналов и управления.
Читаемость и естественность материала подчеркнуты на всем протяжении
текст.

Характеристики

Обширный охват обучения производительности, включая Widrow-Hoff
правило, обратное распространение и несколько улучшений обратного распространения ошибки, такие как
сопряженный градиент и вариации Левенберга-Марквардта.

Обе сети прямого распространения (включая многослойные и радиальные сети)
подробно описаны периодические сетевые тренинги. Текст также охватывает
Байесовская регуляризация и методы обучения раннего прекращения, которые обеспечивают
способность к обобщению сети.

Ассоциативные и конкурентные сети, включая карты характеристик и обучение
векторное квантование, объясняются с помощью простых строительных блоков.

Глава практических советов по аппроксимации функций, шаблон
приложения для распознавания, кластеризации и прогнозирования включены, а также
с пятью главами, в которых представлены подробные примеры из реальной жизни.

Подробные примеры, множество решенных задач и исчерпывающий
демонстрационное программное обеспечение.

Дополнительные упражнения, включающие использование MATLAB, встроены в каждое
глава и набор нейронных сетей.
В демонстрациях используется MATLAB для иллюстрации важных концепций.
Кроме того, простая организация книги — с каждой главой
разделен на следующие разделы: цели, теория и примеры,
Резюме результатов, решенные проблемы, эпилог, дополнительная литература и
Упражнения — отличный инструмент для обучения и продолжения
Справка.

Новое во 2-м издании

2-е издание содержит новые главы по обобщению, динамическому
Сети, радиальные сети, вопросы практического обучения, а также
пять новых глав по тематическим исследованиям из реального мира. Кроме того, большой
В каждую главу добавлено несколько новых домашних заданий.

Получение книги

Бесплатная электронная версия книги на 1012 страницах (11,4 МБ PDF) может быть
скачал отсюда.Несколько
сжатое 800-страничное издание книги в мягкой обложке можно заказать по адресу
Amazon.

Связанные ресурсы

Transparency Masters (Нумерация глав в прозрачной пленке).
masters следует за электронной версией текста.)

Видео-лекции

• Видеолекции для 15-недельного курса, охватывающие большую часть учебника:
  можно получить в Инженерном колледже государственного университета Оклахомы,
  Офис по развитию архитектуры и технологий.Свяжитесь с Натаном Краганом,
  Менеджер отдела технической поддержки, (405)744-9227

Данные для тематических исследований

Демонстрации проектирования нейронных сетей

% PDF-1.4
%
1 0 obj
>
endobj
4 0 obj
(Небольшое предисловие)
endobj
5 0 obj
>
endobj
8 0 объект
(I От биологии к формализации \ 205 мотивация, философия, история и реализация нейронных моделей)
endobj
9 0 объект
>
endobj
12 0 объект
(1 Введение, мотивация и история)
endobj
13 0 объект
>
endobj
16 0 объект
(1.1 Почему нейронные сети?)
endobj
17 0 объект
>
endobj
20 0 объект
(1.1.1 Правило 100 шагов)
endobj
21 0 объект
>
endobj
24 0 объект
(1.1.2 Примеры простых приложений)
endobj
25 0 объект
>
endobj
28 0 объект
(1.2 История нейронных сетей)
endobj
29 0 объект
>
endobj
32 0 объект
(1.2.1 Начало)
endobj
33 0 объект
>
endobj
36 0 объект
(1.2.2 Золотой век)
endobj
37 0 объект
>
endobj
40 0 obj
(1.2.3 Долгое молчание и медленная реконструкция)
endobj
41 0 объект
>
endobj
44 0 объект
(1.2.4 Ренессанс)
endobj
45 0 объект
>
endobj
48 0 объект
(Упражнения)
endobj
49 0 объект
>
endobj
52 0 объект
(2 биологические нейронные сети)
endobj
53 0 объект
>
endobj
56 0 объект
(2.1 Нервная система позвоночных)
endobj
57 0 объект
>
endobj
60 0 obj
(2.1.1 Периферическая и центральная нервная система)
endobj
61 0 объект
>
endobj
64 0 объект
(2.1.2 Головной мозг)
endobj
65 0 объект
>
endobj
68 0 объект
(2.1.3 Мозжечок)
endobj
69 0 объект
>
endobj
72 0 объект
(2.1.4 Промежуточный мозг)
endobj
73 0 объект
>
endobj
76 0 объект
(2.1.5 Ствол мозга)
endobj
77 0 объект
>
endobj
80 0 объект
(2.2 Нейрон)
endobj
81 0 объект
>
endobj
84 0 объект
(2.2.1 Компоненты)
endobj
85 0 объект
>
endobj
88 0 объект
(2.2.2 Электрохимические процессы в нейроне)
endobj
89 0 объект
>
endobj
92 0 объект
(2.3 рецепторные клетки)
endobj
93 0 объект
>
endobj
96 0 объект
(2.3.1 Различные типы)
endobj
97 0 объект
>
endobj
100 0 объект
(2.3.2 Обработка информации в нервной системе)
endobj
101 0 объект
>
endobj
104 0 объект
(2.3.3 Светочувствительные органы)
endobj
105 0 объект
>
endobj
108 0 объект
(2.4 Количество нейронов в живых организмах)
endobj
109 0 объект
>
endobj
112 0 объект
(2.5 Технические нейроны как карикатура на биологию)
endobj
113 0 объект
>
endobj
116 0 объект
(Упражнения)
endobj
117 0 объект
>
endobj
120 0 объект
(3 компонента искусственных нейронных сетей \ (фундаментальные \))
endobj
121 0 объект
>
endobj
124 0 объект
(3.1 Понятие времени в нейронных сетях)
endobj
125 0 объект
>
endobj
128 0 объект
(3.2 Компоненты нейронных сетей)
endobj
129 0 объект
>
endobj
132 0 объект
(3.2.1 Подключения)
endobj
133 0 объект
>
endobj
136 0 объект
(3.2.2 Функция распространения и сетевой вход)
endobj
137 0 объект
>
endobj
140 0 объект
(3.2.3 Активация)
endobj
141 0 объект
>
endobj
144 0 объект
(3.2.4 Пороговое значение)
endobj
145 0 объект
>
endobj
148 0 объект
(3.2.5 Функция активации)
endobj
149 0 объект
>
endobj
152 0 объект
(3.2.6 Общие функции активации)
endobj
153 0 объект
>
endobj
156 0 объект
(3.2.7 Функция вывода)
endobj
157 0 объект
>
endobj
160 0 объект
(3.2.8 Стратегия обучения)
endobj
161 0 объект
>
endobj
164 0 объект
(3.3 Сетевые топологии)
endobj
165 0 объект
>
endobj
168 0 объект
(3.3.1 Обратная связь)
endobj
169 0 объект
>
endobj
172 0 объект
(3.3.2 Рекуррентные сети)
endobj
173 0 объект
>
endobj
176 0 объект
(3.3.3 Полностью связанные сети)
endobj
177 0 объект
>
endobj
180 0 объект
(3.4 нейрон смещения)
endobj
181 0 объект
>
endobj
184 0 объект
(3.5 Представление нейронов)
endobj
185 0 объект
>
endobj
188 0 объект
(3.6 Порядков активации)
endobj
189 0 объект
>
endobj
192 0 объект
(3.6.1 Синхронная активация)
endobj
193 0 объект
>
endobj
196 0 объект
(3.6.2 Асинхронная активация)
endobj
197 0 объект
>
endobj
200 0 объект
(3.7 Ввод и вывод данных)
endobj
201 0 объект
>
endobj
204 0 объект
(Упражнения)
endobj
205 0 объект
>
endobj
208 0 объект
(4 Основы обучения и обучающие образцы \ (фундаментальные \))
endobj
209 0 объект
>
endobj
212 0 объект
(4.1 Парадигмы обучения)
endobj
213 0 объект
>
endobj
216 0 объект
(4.1.1 Обучение без учителя)
endobj
217 0 объект
>
endobj
220 0 объект
(4.1.2 Обучение с подкреплением)
endobj
221 0 объект
>
endobj
224 0 объект
(4.1.3 Обучение с учителем)
endobj
225 0 объект
>
endobj
228 0 объект
(4.1.4 Офлайн или онлайн обучение?)
endobj
229 0 объект
>
endobj
232 0 объект
(4.1.5 Вопросы заранее)
endobj
233 0 объект
>
endobj
236 0 объект
(4.2 Образцы обучения и обучающий вклад)
endobj
237 0 объект
>
endobj
240 0 объект
(4.3 Использование обучающих выборок)
endobj
241 0 объект
>
endobj
244 0 объект
(4.3.1 Деление обучающей выборки)
endobj
245 0 объект
>
endobj
248 0 объект
(4.3.2 Порядок представления паттернов)
endobj
249 0 объект
>
endobj
252 0 объект
(4.4 Кривая обучения и измерение ошибок)
endobj
253 0 объект
>
endobj
256 0 объект
(4.4.1 Когда мы перестанем учиться?)
endobj
257 0 объект
>
endobj
260 0 объект
(4.5 Процедуры оптимизации градиента)
endobj
261 0 объект
>
endobj
264 0 объект
(4.5.1 Проблемы градиентных процедур)
endobj
265 0 объект
>
endobj
268 0 объект
(4.6 Примерные проблемы)
endobj
269 ​​0 объект
>
endobj
272 0 объект
(4.6.1 Логические функции)
endobj
273 0 объект
>
endobj
276 0 объект
(4.6.2 Функция четности)
endobj
277 0 объект
>
endobj
280 0 объект
(4.6.3 Задача о двух спиралях)
endobj
281 0 объект
>
endobj
284 0 объект
(4.6.4 Задача о шахматной доске)
endobj
285 0 объект
>
endobj
288 0 объект
(4.6.5 Функция идентичности)
endobj
289 0 объект
>
endobj
292 0 объект
(4.6.6 Другие примерные проблемы)
endobj
293 0 объект
>
endobj
296 0 объект
(4.7 правило Хебба)
endobj
297 0 объект
>
endobj
300 0 объект
(4.7.1 Исходное правило)
endobj
301 0 объект
>
endobj
304 0 объект
(4.7.2 Обобщенная форма)
endobj
305 0 объект
>
endobj
308 0 объект
(Упражнения)
endobj
309 0 объект
>
endobj
312 0 объект
(II Парадигмы контролируемой обучающей сети)
endobj
313 0 объект
>
endobj
316 0 объект
(5 Персептрон, обратное распространение и его варианты)
endobj
317 0 объект
>
endobj
320 0 объект
(5.1 Однослойный персептрон)
endobj
321 0 объект
>
endobj
324 0 объект
(5.1.1 Алгоритм обучения персептрона и теорема сходимости)
endobj
325 0 объект
>
endobj
328 0 объект
(5.1.2 Правило дельты)
endobj
329 0 объект
>
endobj
332 0 объект
(5.2 Линейная разделимость)
endobj
333 0 объект
>
endobj
336 0 объект
(5.3 Многослойный персептрон)
endobj
337 0 объект
>
endobj
340 0 объект
(5.4 Обратное распространение ошибки)
endobj
341 0 объект
>
endobj
344 0 объект
(5.4.1 Вывод)
endobj
345 0 объект
>
endobj
348 0 объект
(5.4.2 Обратное распространение кипения до правила дельты)
endobj
349 0 объект
>
endobj
352 0 объект
(5.4.3 Выбор скорости обучения)
endobj
353 0 объект
>
endobj
356 0 объект
(5.5 Устойчивое обратное распространение)
endobj
357 0 объект
>
endobj
360 0 объект
(5.5.1 Адаптация весов)
endobj
361 0 объект
>
endobj
364 0 объект
(5.5.2 Динамическая регулировка скорости обучения)
endobj
365 0 объект
>
endobj
368 0 объект
(5.5.3 Rprop на практике)
endobj
369 0 объект
>
endobj
372 0 объект
(5.6 Дальнейшие вариации и расширения обратного распространения ошибки)
endobj
373 0 объект
>
endobj
376 0 объект
(5.6.1 Срок действия)
endobj
377 0 объект
>
endobj
380 0 объект
(5.6.2 Устранение плоских пятен)
endobj
381 0 объект
>
endobj
384 0 объект
(5.6.3 Обратное распространение второго порядка)
endobj
385 0 объект
>
endobj
388 0 объект
(5.6.4 Снижение веса)
endobj
389 0 объект
>
endobj
392 0 объект
(5.6.5 Подрезка и оптимальное повреждение мозга)
endobj
393 0 объект
>
endobj
396 0 объект
(5.7 Начальная конфигурация многослойного персептрона)
endobj
397 0 объект
>
endobj
400 0 obj
(5.7.1 Количество слоев)
endobj
401 0 объект
>
endobj
404 0 объект
(5.7.2 Количество нейронов)
endobj
405 0 объект
>
endobj
408 0 объект
(5.7.3 Выбор функции активации)
endobj
409 0 объект
>
endobj
412 0 объект
(5.7.4 Инициализация весов)
endobj
413 0 объект
>
endobj
416 0 объект
(5.8 Проблема кодирования 8-3-8 и связанные с ней проблемы)
endobj
417 0 объект
>
endobj
420 0 объект
(Упражнения)
endobj
421 0 объект
>
endobj
424 0 объект
(6 радиальных базисных функций)
endobj
425 0 объект
>
endobj
428 0 объект
(6.1 Компоненты и конструкция)
endobj
429 0 объект
>
endobj
432 0 объект
(6.2 Обработка информации в сети RBF)
endobj
433 0 объект
>
endobj
436 0 объект
(6.2.1 Обработка информации в нейронах RBF)
endobj
437 0 объект
>
endobj
440 0 объект
(6.2.2 Аналитические мысли перед тренировкой)
endobj
441 0 объект
>
endobj
444 0 объект
(6.3 Обучение сетей RBF)
endobj
445 0 объект
>
endobj
448 0 объект
(6.3.1 Центры и ширина нейронов RBF)
endobj
449 0 объект
>
endobj
452 0 объект
(6.4 Растущие сети RBF)
endobj
453 0 объект
>
endobj
456 0 объект
(6.4.1 Добавление нейронов)
endobj
457 0 объект
>
endobj
460 0 объект
(6.4.2 Ограничение количества нейронов)
endobj
461 0 объект
>
endobj
464 0 объект
(6.4.3 Удаление нейронов)
endobj
465 0 объект
>
endobj
468 0 объект
(6.5 Сравнение сетей RBF и многослойных персептронов)
endobj
469 0 объект
>
endobj
472 0 объект
(Упражнения)
endobj
473 0 объект
>
endobj
476 0 объект
(7 рекуррентных сетей, подобных перцептрону \ (зависит от главы 5 \))
endobj
477 0 объект
>
endobj
480 0 объект
(7.1 Иорданские сети)
endobj
481 0 объект
>
endobj
484 0 объект
(7.2 Сети Элмана)
endobj
485 0 объект
>
endobj
488 0 объект
(7.3 Обучающие повторяющиеся сети)
endobj
489 0 объект
>
endobj
492 0 объект
(7.3.1 Разворачиваясь во времени)
endobj
493 0 объект
>
endobj
496 0 объект
(7.3.2 Принуждение учителя)
endobj
497 0 объект
>
endobj
500 0 объект
(7.3.3 Рекуррентное обратное распространение)
endobj
501 0 объект
>
endobj
504 0 объект
(7.3.4 Обучение с эволюцией)
endobj
505 0 объект
>
endobj
508 0 объект
(8 сетей Хопфилда)
endobj
509 0 объект
>
endobj
512 0 объект
(8.1 Вдохновленный магнетизмом)
endobj
513 0 объект
>
endobj
516 0 объект
(8.2 Структура и функциональность)
endobj
517 0 объект
>
endobj
520 0 объект
(8.2.1 Вход и выход сети Хопфилда)
endobj
521 0 объект
>
endobj
524 0 объект
(8.2.2 Значение веса)
endobj
525 0 объект
>
endobj
528 0 объект
(8.2.3 Изменение состояния нейронов)
endobj
529 0 объект
>
endobj
532 0 объект
(8.3 Создание матрицы весов)
endobj
533 0 объект
>
endobj
536 0 объект
(8.4 Автоассоциация и традиционное приложение)
endobj
537 0 объект
>
endobj
540 0 объект
(8.5 Гетероассоциация и аналогии с хранением нейронных данных)
endobj
541 0 объект
>
endobj
544 0 объект
(8.5.1 Создание гетероассоциативной матрицы)
endobj
545 0 объект
>
endobj
548 0 объект
(8.5.2 Стабилизация гетероассоциаций)
endobj
549 0 объект
>
endobj
552 0 объект
(8.5.3 Биологическая мотивация гетерассоциации)
endobj
553 0 объект
>
endobj
556 0 объект
(8.6 Непрерывные сети Хопфилда)
endobj
557 0 объект
>
endobj
560 0 объект
(Упражнения)
endobj
561 0 объект
>
endobj
564 0 объект
(9 Обучение векторного квантования)
endobj
565 0 объект
>
endobj
568 0 объект
(9.1 О квантовании)
endobj
569 0 объект
>
endobj
572 0 объект
(9.2 Цель LVQ)
endobj
573 0 объект
>
endobj
576 0 объект
(9.3 Использование векторов кодовой книги)
endobj
577 0 объект
>
endobj
580 0 объект
(9.4 Регулировка векторов кодовой книги)
endobj
581 0 объект
>
endobj
584 0 объект
(9.4.1 Порядок обучения)
endobj
585 0 объект
>
endobj
588 0 объект
(9.5 Подключение к нейронным сетям)
endobj
589 0 объект
>
endobj
592 0 объект
(Упражнения)
endobj
593 0 объект
>
endobj
596 0 объект
(III Парадигмы сетей неконтролируемого обучения)
endobj
597 0 объект
>
endobj
600 0 obj
(10 самоорганизующихся функциональных карт)
endobj
601 0 объект
>
endobj
604 0 объект
(10.1 Структура)
endobj
605 0 объект
>
endobj
608 0 объект
(10.2 Функциональность и интерпретация результатов)
endobj
609 0 объект
>
endobj
612 0 объект
(10.3 Обучение)
endobj
613 0 объект
>
endobj
616 0 объект
(10.3.1 Функция топологии)
endobj
617 0 объект
>
endobj
620 0 объект
(10.3.2 Монотонно убывающая скорость обучения и соседство)
endobj
621 0 объект
>
endobj
624 0 объект
(10.4 Примеры)
endobj
625 0 объект
>
endobj
628 0 объект
(10.4.1 Топологические дефекты)
endobj
629 0 объект
>
endobj
632 0 объект
(10.5 Регулировка разрешения и скорости обучения в зависимости от положения)
endobj
633 0 объект
>
endobj
636 0 объект
(10.6 Применение)
endobj
637 0 объект
>
endobj
640 0 объект
(10.6.1 Взаимодействие с сетями RBF)
endobj
641 0 объект
>
endobj
644 0 объект
(10,7 вариаций)
endobj
645 0 объект
>
endobj
648 0 объект
(10.7.1 Нейронный газ)
endobj
649 0 объект
>
endobj
652 0 объект
(10.7.2 Мульти-SOM)
endobj
653 0 объект
>
endobj
656 0 объект
(10.7.3 Мульти-нейронный газ)
endobj
657 0 объект
>
endobj
660 0 объект
(10.7.4 Рост нервного газа)
endobj
661 0 объект
>
endobj
664 0 объект
(Упражнения)
endobj
665 0 объект
>
endobj
668 0 объект
(11 Теория адаптивного резонанса)
endobj
669 0 объект
>
endobj
672 0 объект
(11.1 Задача и структура сети ART)
endobj
673 0 объект
>
endobj
676 0 объект
(11.1.1 Резонанс)
endobj
677 0 объект
>
endobj
680 0 объект
(11.2 Процесс обучения)
endobj
681 0 объект
>
endobj
684 0 объект
(11.2.1 Ввод шаблона и обучение сверху вниз)
endobj
685 0 объект
>
endobj
688 0 объект
(11.2.2 Резонансное и восходящее обучение)
endobj
689 0 объект
>
endobj
692 0 объект
(11.2.3 Добавление выходного нейрона)
endobj
693 0 объект
>
endobj
696 0 объект
(11.3 Расширения)
endobj
697 0 объект
>
endobj
700 0 объект
(IV Экскурсии, приложения и регистры)
endobj
701 0 объект
>
endobj
704 0 объект
(Экскурс: кластерный анализ и региональные и онлайн-обучаемые области)
endobj
705 0 объект
>
endobj
708 0 объект
(А.1 кластеризация k-средних)
endobj
709 0 объект
>
endobj
712 0 объект
(A.2 k-ближайший сосед)
endobj
713 0 объект
>
endobj
716 0 объект
(A.3 — ближайший сосед)
endobj
717 0 объект
>
endobj
720 0 объект
(А.4 Коэффициент силуэта)
endobj
721 0 объект
>
endobj
724 0 объект
(A.5 Региональные и интерактивные поля для изучения)
endobj
725 0 объект
>
endobj
728 0 объект
(A.5.1 Структура ROLF)
endobj
729 0 объект
>
endobj
732 0 объект
(A.5.2 Обучение ROLF)
endobj
733 0 объект
>
endobj
736 0 объект
(A.5.3 Оценка ROLF)
endobj
737 0 объект
>
endobj
740 0 объект
(А.5.4 Сравнение с популярными методами кластеризации)
endobj
741 0 объект
>
endobj
744 0 объект
(A.5.5 Инициализация радиусов, скорости обучения и множителя)
endobj
745 0 объект
>
endobj
748 0 объект
(A.5.6 Примеры применения)
endobj
749 0 объект
>
endobj
752 0 объект
(Упражнения)
endobj
753 0 объект
>
endobj
756 0 объект
(B Excursus: нейронные сети, используемые для прогнозирования)
endobj
757 0 объект
>
endobj
760 0 объект
(B.1 О временных рядах)
endobj
761 0 объект
>
endobj
764 0 объект
(B.2 Прогнозирование на один шаг вперед)
endobj
765 0 объект
>
endobj
768 0 объект
(Б.3 Прогноз на два шага вперед)
endobj
769 0 объект
>
endobj
772 0 объект
(B.3.1 Рекурсивное прогнозирование на два шага вперед)
endobj
773 0 объект
>
endobj
776 0 объект
(B.3.2 Прямое прогнозирование на два шага вперед)
endobj
777 0 объект
>
endobj
780 0 объект
(B.4 Дополнительные подходы к оптимизации для прогнозирования)
endobj
781 0 объект
>
endobj
784 0 объект
(B.4.1 Изменение временных параметров)
endobj
785 0 объект
>
endobj
788 0 объект
(B.4.2 Гетерогенное предсказание)
endobj
789 0 объект
>
endobj
792 0 объект
(B.5 Замечания по прогнозированию цен на акции)
endobj
793 0 объект
>
endobj
796 0 объект
(C Excursus: обучение с подкреплением)
endobj
797 0 объект
>
endobj
800 0 объект
(С.1 Структура системы)
endobj
801 0 объект
>
endobj
804 0 объект
(C.1.1 Сеточный мир)
endobj
805 0 объект
>
endobj
808 0 объект
(C.1.2 Агент и среда)
endobj
809 0 объект
>
endobj
812 0 объект
(C.1.3 Состояния, ситуации и действия)
endobj
813 0 объект
>
endobj
816 0 объект
(C.1.4 Вознаграждение и возврат)
endobj
817 0 объект
>
endobj
820 0 объект
(C.1.5 Политика)
endobj
821 0 объект
>
endobj
824 0 объект
(C.2 Процесс обучения)
endobj
825 0 объект
>
endobj
828 0 объект
(C.2.1 Стратегии вознаграждения)
endobj
829 0 объект
>
endobj
832 0 объект
(С.2.2 Функция состояния-значения)
endobj
833 0 объект
>
endobj
836 0 объект
(C.2.3 Метод Монте-Карло)
endobj
837 0 объект
>
endobj
840 0 объект
(C.2.4 Обучение разнице во времени)
endobj
841 0 объект
>
endobj
844 0 объект
(C.2.5 Функция «действие-значение»)
endobj
845 0 объект
>
endobj
848 0 объект
(C.2.6 Q обучение)
endobj
849 0 объект
>
endobj
852 0 объект
(C.3 Примеры приложений)
endobj
853 0 объект
>
endobj
856 0 объект
(C.3.1 Гаммон TD)
endobj
857 0 объект
>
endobj
860 0 объект
(В.3.2 Автомобиль в яме)
endobj
861 0 объект
>
endobj
864 0 объект
(С.3.3 Балансир столбов)
endobj
865 0 объект
>
endobj
868 0 объект
(C.4 Обучение с подкреплением в связи с нейронными сетями)
endobj
869 0 объект
>
endobj
872 0 объект
(Упражнения)
endobj
873 0 объект
>
endobj
876 0 объект
(Библиография)
endobj
877 0 объект
>
endobj
880 0 объект
(Список рисунков)
endobj
881 0 объект
>
endobj
884 0 объект
(Индекс)
endobj
885 0 объект
>
endobj
889 0 obj>
ручей
x + 2T0

Выполнение вывода с использованием предварительно обученной нейронной сети

В предыдущем блоге об искусственном интеллекте Алгоритмы машинного обучения AI — как работает нейронная сеть мы рассмотрели основы того, как нейронная сеть структурирована с помощью слоев и как такая сеть обучена.И хотя есть много шагов и над чем нужно подумать, к счастью, существует множество фреймворков ИИ и готовых сетей, которые могут сделать за вас большую часть тяжелой работы.

Итак, теперь, когда мы рассмотрели, как работает нейронная сеть, давайте посмотрим, как нейронная сеть, созданная из инфраструктуры искусственного интеллекта, может быть запущена на мобильной платформе Qualcomm® Snapdragon ™.

Платформа Snapdragon хорошо подходит для выполнения логического вывода в нейронных сетях на периферии, потому что она предлагает разработчикам гибкость для выполнения логического вывода, чтобы убедиться, что она должным образом интегрируется в соответствии с требованиями к производительности и мощности своего DSP Qualcomm® Hexagon ™, Qualcomm® Adreno ™ GPU или Qualcomm® Kryo ™ CPU.Кроме того, он обеспечивает поддержку нейронных сетей, созданных в двух популярных фреймворках: Caffe2 и TensorFlow. Он также поддерживает открытый формат ONNX, что означает, что он также может использовать нейронные сети, обученные любой другой структурой, которая выводит данные в ONNX.

Это возможно благодаря инструментам и API, предоставляемым Qualcomm® Neural Processing SDK, который включает:

• , включающий наш Neural Processing SDK в приложение
• преобразование нейронной сети в контейнерный формат глубокого обучения (DLC)
• загрузка и запуск нейронной сети с помощью API SDK для нейронной обработки

Для получения дополнительной информации о SDK для нейронной обработки, мы приглашаем вас ознакомиться с нашей документацией.

Следующая диаграмма иллюстрирует весь рабочий процесс, включая создание обученной нейронной сети:

Давайте рассмотрим каждую фазу более подробно.

Шаги по настройке и использованию среды разработки SDK в Ubuntu [1] подробно описаны в нашем Справочном руководстве Neural Processing SDK. Общие шаги:

• Настройка инфраструктуры AI (Caffe2, TensorFlow или ONNX)
• Настройка Python
• Установите Android NDK (при создании собственных приложений CPP)
• Установите Android SDK (требуется для сборки Android APK, включенный в SDK)
• Получите SDK и разархивируйте его
• Запустите проверку зависимостей для пакетов Python
• Запустите сценарий (-ы) установки
• Установите соответствующие переменные среды

Как только это будет После настройки разработчики могут загрузить и запустить нейронную сеть из кода для выполнения логического вывода.

Фреймворки ИИ выводят свои обученные нейронные сети в виде файла данных или набора файлов в зависимости от фреймворка и типа базовой нейронной сети. Например, TensorFlow может выводить замороженную модель TensorFlow (файл .pb) или пару метафайлов контрольных точек и графиков. Файлы нейронных сетей, такие как эти, содержат разнообразную информацию об обученной нейронной сети, включая структуру сети, определение, веса и смещения, установленные во время обучения, и другие.

После создания файлов из фреймворка следующим шагом будет настройка конвейера для их преобразования в формат, подходящий для выполнения на платформе Snapdragon. Для поддержки этого мы разработали наш формат контейнера глубокого обучения (DLC), который представляет собой формат файла, который API-интерфейс SDK для нейронной обработки загружает и запускает на платформе Snapdragon. Наш SDK для нейронной обработки также включает инструменты командной строки для Caffe2, TensorFlow и ONNX для преобразования файлов нейронной сети из соответствующей платформы в DLC.

Во время преобразования разработчики имеют возможность выполнить квантование, чтобы уменьшить размер файла и потенциально снизить вычислительную мощность и энергопотребление, необходимые для выполнения логического вывода. Квантование достигает этого путем преобразования представления сетевых параметров из 32-битных чисел с плавающей запятой в 8-битные с фиксированной точкой. На этом этапе разработчики также имеют возможность добавить разделы HTA, чтобы воспользоваться преимуществами Hexagon Tensor Accelerator, установленного на таких устройствах, как мобильная платформа Qualcomm® Snapdragon ™ 855.

Библиотека времени выполнения нашего SDK для нейронной обработки предоставляет ряд компонентов (см. Диаграмму ниже) для использования преимуществ оборудования Snapdragon для выполнения вывода обученной модели:

Основными компонентами библиотеки времени выполнения нашего SDK для нейронной обработки являются:

• DL Container Loader: Загружает файл DLC, созданный одним из инструментов преобразования SDK Neural Processing.
• Проверка модели: Проверяет, что загруженный файл DLC поддерживается [2] требуемой средой выполнения.
• Механизм выполнения: Выполняет загруженную модель в запрошенных средах выполнения, включая сбор информации профилирования и поддержку определяемых пользователем уровней (UDL).
• Логика разделения: Обрабатывает модель, включая UDL и информацию о проверке, и при необходимости создает разбиение модели на подмодели. Для UDL эта логика прерывает выполнение до и после UDL, чтобы разрешить выполнение UDL. Если включен резервный режим ЦП, модель разделяется между уровнями, поддерживаемыми целевой средой выполнения, и уровнями, поддерживаемыми средой выполнения ЦП.
• Время выполнения ЦП: Выполняет модель на ЦП Kryo, поддерживая 32-битное выполнение с плавающей запятой или 8-битное квантованное выполнение.
• Время работы графического процессора: Запуск модели на графическом процессоре Adreno, поддерживая гибридный или полный 16-битный режимы с плавающей запятой.
• DSP Runtime: Запускает модель на Hexagon DSP с использованием Hexagon Vector Extensions (HVX [3]), которые хорошо подходят для векторных операций, обычно используемых в алгоритмах машинного обучения.
• AI Processor (AIP) Runtime: Запускает модель на Hexagon DSP с использованием Q6, Hexagon NN и HTA.

Особо следует отметить AIP, который представляет собой программную абстракцию среды выполнения Q6, HVX и HTA в единый объект (AIP), который управляет выполнением модели нейронной сети для всех трех функций оборудования, как показано на диаграмме. ниже:

Разработчики, которые загружают модель с помощью API SDK для нейронной обработки и выбирают среду выполнения AIP в качестве цели, будут иметь части модели, работающие на HTA, а части на HVX, с использованием библиотеки ускорения HexNN с ускорением HVX.

Общие шаги для того, чтобы все это работало во время выполнения с использованием нашего API SDK для нейронной обработки, следующие:

• Получить и выбрать доступные ядра времени выполнения для выполнения сети на Hexagon DSP, Adreno GPU или Kryo CPU
• Load файл DLC
• Выполнение сети
• Считывание выходных данных сети и обработка в соответствии с бизнес-логикой приложения

Наш пакет SDK для нейронной обработки предоставляет ряд учебных пособий, демонстрирующих это.Наиболее примечательными являются руководства по C ++ и Android, в которых показано, как использовать API SDK для нейронной обработки для загрузки сети из файла DLC и выполнения этой сети для выполнения логического вывода.

Хотя хорошее понимание нейронных сетей важно, набор инструментов, такой как предоставляемый нашим SDK нейронной обработки, помогает упростить процесс переноса обученной нейронной сети на мобильную платформу Snapdragon до нескольких si

Нейронная сеть

---

2

Неожиданная сетевая активность в незрелом мозге

Октябрь25, 2018 — Одна из выдающихся загадок коры головного мозга заключается в том, как отдельные нейроны развивают правильные синаптические связи для формирования крупномасштабных распределенных сетей. Теперь ученые получили роман …

---

Мозговые волны, обнаруженные в мини-мозге, выращенном в тарелке

29 августа 2019 г. — Ученые создали миниатюрный мозг из стволовых клеток, которые создали функциональные нейронные сети. Несмотря на то, что они в миллион раз меньше человеческого мозга, эти выращенные в лаборатории мозги являются первыми…

---

Когнитивная тренировка снижает депрессию, восстанавливает поврежденную структуру мозга и возможности взаимодействия после травматической травмы мозга

29 мая 2018 г. — Новое исследование показывает, что определенные упражнения для когнитивных тренировок могут помочь уменьшить депрессию и улучшить здоровье мозга у людей спустя годы после перенесенной черепно-мозговой травмы …

---

Три способа изучения органической химии изменяют мозг

7 марта 2019 г. — Новое исследование с использованием нескольких методов визуализации показывает, что изучение научной информации приводит к изменениям фактической структуры областей мозга, связанных с памятью, из-за кодирования…

---

Упражнение активирует нейронные сети памяти у пожилых людей

25 апреля 2019 г. — Новое исследование здоровых пожилых людей показывает, что всего одна тренировка увеличивает активацию цепей мозга, связанных с памятью, включая гиппокамп, которая с возрастом сужается …

---

Как наш мозг генерирует сознание — и теряет его

1 мая 2019 г. — В первом в своем роде исследовании исследователи использовали двухфотонную визуализацию кальция in vivo у мышей, чтобы изучить изменения в локальном репертуаре микросостояний нейронов во время…

---

ИИ может изменить то, как мы отслеживаем структурное состояние гражданской инфраструктуры

18 ноября 2019 г. — Ученые разработали новый алгоритм машинного обучения (ИИ), который может изменить способ мониторинга основных объектов инфраструктуры, таких как плотины и …

---

Тренируйте свой мозг, измените свой мозг

14 апреля 2019 г. — Менее одного часа тренировки мозга с нейробиоуправлением приводит к усилению нейронных связей и коммуникации между областями мозга.Это главный вывод нового исследования. Согласно …

---

Полностью оптическая дифракционная нейронная сеть сокращает разрыв в производительности с помощью электронных нейронных сетей

13 августа 2019 г. — Новая статья демонстрирует явные улучшения в работе логического вывода и обобщения дифракционной оптической нейронной сети …

---

Антидепрессант, эффективный при лечении «ленивого глаза» у взрослых

30 сентября 2020 г. — Исследователи выяснили, как субанестетик кетамин, который используется для снятия боли и в качестве антидепрессанта у людей, эффективен при лечении амблиопии у взрослых, заболевании головного мозга, широко известном как…

---

6,6. Сверточные нейронные сети (LeNet) — погрузитесь в документацию по глубокому обучению 0.15.1

Теперь у нас есть все ингредиенты, необходимые для сборки полнофункционального
CNN. В нашем предыдущем столкновении с данными изображения мы применили softmax
регрессионная модель (раздел 3.6) и модель MLP
(Раздел 4.2) к фотографиям одежды в
Набор данных Fashion-MNIST. Сделать такие данные доступными для регрессии softmax
и MLP, мы сначала сгладили каждое изображение из матрицы \ (28 \ times28 \)
в \ (784 \) -мерный вектор фиксированной длины, а затем
обработал их полносвязными слоями.Теперь, когда у нас есть ручка
сверточные слои, мы можем сохранить пространственную структуру в наших изображениях.
В качестве дополнительного преимущества замены полносвязных слоев на
сверточные слои, нам понравятся более экономные модели, которые
требуется гораздо меньше параметров.

В этом разделе мы представим LeNet , один из первых опубликованных
CNN привлекают широкое внимание своей работой в области компьютерного зрения
задачи. Модель была представлена ​​(и названа в честь) Яном ЛеКуном, затем
исследователь в AT&T Bell Labs, с целью распознавания рукописных
цифры на изображениях [LeCun et al., 1998]. Эта работа
представляет собой кульминацию десятилетия исследований по разработке
технологии. В 1989 году ЛеКун опубликовал первое исследование, в котором успешно
обучать CNN через обратное распространение.

В то время LeNet достиг выдающихся результатов, соответствующих производительности
машин опорных векторов, то доминирующий подход в контролируемых
обучение. В конечном итоге LeNet был адаптирован для распознавания цифр для
обработка депозитов в банкоматах. По сей день некоторые банкоматы все еще работают
код, который Янн и его коллега Леон Ботту написали в 1990-х!

6.6.1. LeNet¶

На высоком уровне LeNet (LeNet-5) состоит из двух частей: (i)
сверточный кодер, состоящий из двух сверточных слоев; и (ii) a
плотный блок, состоящий из трех полносвязных слоев; Архитектура
Обобщено на рис. 6.6.1.

Рис. 6.6.1 Поток данных в LeNet. Ввод — это рукописная цифра, на выходе —
вероятность более 10 возможных исходов.

Базовыми единицами в каждом сверточном блоке являются сверточный слой,
функция активации сигмовидной кишки и последующая операция среднего пула.Обратите внимание, что хотя ReLU и max-pooling работают лучше, эти открытия
еще не производился в 1990-е годы. Каждый сверточный слой использует
\ (5 \ times 5 \) ядро ​​и сигмовидная функция активации. Эти слои
отображать пространственно расположенные входы для ряда двумерных объектов
карты, обычно увеличивающие количество каналов. Первое
сверточный слой имеет 6 выходных каналов, а второй — 16. Каждый
\ (2 \ times2 \) операция объединения (шаг 2) уменьшает размерность на
коэффициент \ (4 \) за счет пространственной понижающей дискретизации.Сверточный блок
испускает вывод с формой, заданной (размер пакета, номер канала,
высота ширина).

Чтобы передать вывод сверточного блока в плотный блок,
мы должны сгладить каждый образец в мини-партии. Другими словами, берем
этот четырехмерный ввод и преобразовать его в двухмерный
ввод, ожидаемый полностью подключенными слоями: напомним, что
двумерное представление, которое мы желаем, использует первое
измерение для индексации примеров в минипакете, а второе — для указания
плоское векторное представление каждого примера.Плотный блок LeNet имеет
три полностью связанных уровня с 120, 84 и 10 выходами,
соответственно. Поскольку мы все еще проводим классификацию,
10-мерный выходной слой соответствует количеству возможных выходных
классы.

Достигая момента, когда вы действительно понимаете, что происходит
внутри LeNet, возможно, потребовалось немного поработать, надеюсь, следующий код
сниппет убедит вас, что реализация таких моделей с помощью современных глубоких
рамки обучения удивительно просты.Нам нужно только создать экземпляр
Последовательный объединяет соответствующие слои в цепочку.

 из d2l импортировать mxnet как d2l
из mxnet импортировать autograd, gluon, init, np, npx
из mxnet.gluon import nn
npx.set_np ()

сеть = nn.Sequential ()
net.add (nn.Conv2D (каналы = 6, размер_ядра = 5, заполнение = 2, активация = 'сигмоид'),
        nn.AvgPool2D (размер_пул = 2, шаги = 2),
        nn.Conv2D (каналы = 16, размер ядра = 5, активация = 'сигмоид'),
        nn.AvgPool2D (размер_пул = 2, шаги = 2),
        # `Dense` преобразует входные данные формы (размер партии, количество
        # каналы, высота, ширина) во вход формы (размер партии,
        # количество каналов * высота * ширина) автоматически по умолчанию
        nn.Плотный (120, активация = 'сигмовидная'),
        nn.Dense (84, активация = 'сигмовидная'),
        nn.Dense (10))
 

 от d2l импортная горелка как d2l
импортный фонарик
из факела импорт нн

класс Reshape (torch.nn.Module):
    def вперед (self, x):
        вернуть x.view (-1, 1, 28, 28)

net = torch.nn.Sequential (
    Изменить форму (),
    nn.Conv2d (1, 6, размер ядра = 5, отступ = 2), nn.Sigmoid (),
    nn.AvgPool2d (размер_ядра = 2, шаг = 2),
    nn.Conv2d (6, 16, размер_ядра = 5), nn.Sigmoid (),
    nn.AvgPool2d (размер_ядра = 2, шаг = 2),
    nn.Свести (),
    nn.Linear (16 * 5 * 5, 120), nn.Sigmoid (),
    nn.Linear (120, 84), nn.Sigmoid (),
    nn.Linear (84, 10))
 

 из d2l импортировать тензорный поток как d2l
импортировать тензорный поток как tf
из tensorflow.distribute import MirroredStrategy, OneDeviceStrategy

def net ():
    вернуть tf.keras.models.Sequential ([
        tf.keras.layers.Conv2D (фильтры = 6, размер_ядра = 5, активация = 'сигмоид',
                               padding = 'такой же'),
        tf.keras.layers.AvgPool2D (pool_size = 2, strides = 2),
        tf.keras.layers.Conv2D (фильтры = 16, размер ядра = 5,
                               активация = 'сигмоид'),
        tf.keras.layers.AvgPool2D (pool_size = 2, strides = 2),
        tf.keras.layers.Flatten (),
        tf.keras.layers.Dense (120, Activation = 'sigmoid'),
        tf.keras.layers.Dense (84, activate = 'sigmoid'),
        tf.keras.layers.Dense (10)])
 

Мы пошли на небольшую вольность с исходной моделью, убрав гауссову
активация в финальном слое. Помимо этого, эта сеть соответствует
оригинальная архитектура LeNet-5.

Путем передачи одноканального (черно-белого) \ (28 \ times 28 \) изображения
через сеть и распечатав форму вывода на каждом слое, мы можем
осмотрите модель, чтобы убедиться, что ее операции соответствуют тому, что мы
ожидаем от рис. 6.6.2.

Рис. 6.6.2 Сжатая нотация для LeNet-5.000

 X = np.random.uniform (размер = (1, 1, 28, 28))
net.initialize ()
для слоя в сети:
    X = слой (X)
    print (имя слоя, 'форма вывода: \ t', X.shape)
 

Форма вывода

 conv0: (1, 6, 28, 28)
Форма вывода pool0: (1, 6, 14, 14)
Форма вывода conv1: (1, 16, 10, 10)
Форма вывода pool1: (1, 16, 5, 5)
Форма вывода Thick0: (1, 120)
Форма вывода плотная1: (1, 84)
Форма вывода density2: (1, 10)
 

 X = резак.
No related posts.