Сколько раз в сутки часовая и минутная стрелки совпадают: «Сколько раз в сутки пересекаются часовая и минутная стрелки часов?»

Содержание

✅ Сколько раз за день пересекаются стрелки часов. Сколько раз в течение суток перекрываются часовая и минутная стрелки

У вас есть аналоговые часы с секундной стрелкой. Сколько раз в день все три стрелки часов накладываются друг на друга?

Задачки, 20 октября 2015 в 13:09

Эта задача — вариант классического вопроса, задававшегося на собеседованиях в Microsoft, когда претендентов спрашивали, сколько раз в день часовая и минутная стрелки встречаются друг с другом. Посколько этот вопрос сейчас стал широко известен, интервьюверы начали использовать его разновидность.

Рассмотрим сначала вариант наиболее ожидаемого решения, математического. Во-первых, представьте ситуацию, когда часовая и минутная стрелки наложились. Все знают, что это происходит в полночь, затем приблизительно в 1:05, 2:10, 3:15 и так далее. Другими словами, они накладываются друг на друга каждый час, за исключением периода от 11:00 до 12:00. В 11:00 более быстрая минутная стрелка находится на 12, а более медленная часовая — на 11:00. До 12:00 дня они друг с другом не встретятся, и поэтому их наложения в районе 11 часов не будет.

Таким образом, за каждый 12-часовой период происходит 11 наложений. Они равномерно распределены во времени, поскольку обе стрелки двигаются с постоянной скоростью. Это означает, что интервалы между наложениями составляют 12/11 часа. Это эквивалентно 1 часу 5 минутам 27 и 3/11 секундам. Поэтому за каждый 12-часовой цикл наложения происходят в периоды, указанные на картинке.

Вернёмся к секундной стрелке. Её наложение на минутную возможно тогда, когда число минут совпадает с числом секунд. Точное наложение происходит в 00:00:00. В целом минутные и секундные стрелки накладыватся лишь на долю секунды. Например, в 12:37:37 секундная стрелка будет показывать на 37, отставая от минутной, которая в это время будет между 37 и 38 и отставать от часовой. Через мгновение минутная и секундная наложатся, но часовой возле них не будет. Т.е. наложения всех трёх стрелок не произойдет.

Секундная стрелка не наложится ни в одном из вариантов на картинке, за исключением полуночи и полудня. Это означает, что финальный ответ на вопрос: дважды в сутки.

А вот ответ, приветствуемый в Google. Секундная стрелка предназначена для показа коротких временных интервалов, а не для сообщения времени с точностью до секунды. Если она не синхронизирована с двумя другими стрелками, это вполне нормально. Под «синхронизацией» здесь понимается, что в полночь и полдень все три стрелки указывают точно на 12. Большинство аналоговых часов всех видов не позволяют вам точно установить секундную стрелку. Нужно было бы извлечь батарейку или подождать, если говорить о механических часах, когда закончится завод пружины, а затем, когда секундная стрелка остановлена, синхронизировать минутную и часовую стрелки друг с другом, после чего дождаться, когда наступит время, показанное на часах, чтобы вернуть батарейку или завести часы.

Чтобы все это проделать, нужно быть маньяком или фанатеть от пунктуальности. Но если вы всего этого не проделаете, секундная стрелка не будет показывать «реального» времени. Она будет отличаться от точных секунд на какую-то величину в случайном интервале, доходящем до 60 секунд. Учитывая случайные расходждения, шансов на то, что все три стрелки когда-либо встретятся, не существует. Этого не случается никогда.

Сколько раз за сутки стрелки часов совпадают в одном положении

Сколько раз в день стрелки часов совпадают?

Часовая стрелка за сутки два раза обходит циферблат часов, а минутная стрелка совершает 24 оборота и 22 раза догоняет часовую. Если взять за время старта время полночи, то 0 часов 0 минут, то минутная сразу убежит вперд и догонит часовую в 1 час 5 минут. Потом в 2 часа 11 минут, затем в 3 часа 16 минут, в 4 часа 22 минуты, в 5 часов 27 минут, в 6 часов 33 минуты, в 7 часов 38 минут, в 8 часов 44 минуты, в 9 часов 49 минут, в 10 часов 55 минут, в 12 часов 00 минут первый круг закончится, стрелки опять вместе и вс начнтся заново. Догонит минутная стрелка часовую в 13 часов 05 минут, в 14 часов 11 минут, в 15 часов 16 минут, в 16 часов 22 минуты, в 17 часов 27 минут, в 18 часов 33 минуты, в 19 часов 38 минут, в 20 часов 44 минуты, в 21 час 49 минут и последний раз стрелки будут вместе в 22 часа 55 минут.

Следующий раз возможен в 0 часов 0 минут, но это уже повторение самого первого раза.

То есть всего 22 раза догоняет минутная стрелка часовую.

Это абсолютно точно (насколько это возможно высчитать, имея в руках старые карманные часы).

Если считать по картинке, то получается совпадений 24 раза. А если взять механические часы и вращать стрелки и при этом подсчитывать, сколько раз стрелки совмещаются, то получается 23 раза. Именно 23, а не 22 и не 24. Так как, сутки начинаются в 00:00 и заканчиваются в 00:00.

Насколько мне известно, в течение одних суток часовая и минутная стрелки часов в общей сложности совпадают 22 раза. Вс дело в том, что часовая и минутная стрелки часов совпадают не один раз в час, а немного реже.

Могу сказать однозначно, что стрелки часов совпадают на циферблате в сутки ровно двадцать четыре раза. Например, в 00.00, а также в 13.05 и 1.05, 14.10 и 2.10, 15.15 и 3.15, 16.20 и 4.20 и так далее, попробуйте сами посчитать.

Я думаю, что стрелки совпадают ровно 24 раза в сутки, по одному разу в каждый час. Вот, например, сейчас 12 часов ровно — стрелки совпали. 1 час 5 минут — стрелки совпали. 2 часа 10 минут — стрелки совпали и так далее.

Минутная и часовая стрелки пересекаются не раз в час, а чуть реже. К примеру, от нуля часов до 1 часа 5 минут проходит не один час, а 65 минут, и так далее. Поэтому получается цифра 11 раз за пол-суток и 22 раза за сутки. Так что, 22 пересечения, именно это окончательная цифра.

В сутки стрелки часов совпадают 22 раза.

Если взять десять суток — 220 раз.

Zmiter ответил почти точно, но если 00:00 это начало новых суток. то они заканчиваются в 23:59:59 и начинаются новые сутки. Правильный ответ 22 раза.

Стрелки часов совпадают столько раз, сколько часов есть в сутках. То есть 24 раза. Если хотите проверить и под рукой у Вас нету часов, то попробуйте воспользоваться картинкой ниже

Но точное время совпадения я сказать не смогу (только в 00-00 и 12-00), так как надо расчитывать скорость движения часовой стрелки.

Сколько Раз В Сутки Три Стрелки Часов Совпадают?

Ответы на поставленный вопрос носят в основном декларативный характер, но не как решение математической задачи. Правильный ответ, возможно, многим покажется неожиданным. Попробуем разобраться в проблеме, не прибегая к сложным приемам. Ясно, что стрелки в определенные периоды времени совпадают. Минутная обгоняет часовую, а секундная, в свою очередь, две ранее названные стрелки. Но речь ведется об одновременном совпадении трех стрелок. Следовательно, достаточно вычислить моменты совмещения минутной и часовой стрелок и определить, где будет находиться в это время секундная стрелка. Циферблат разделен на 12 часов и 60 делений (минут, секунд), которые и будем использовать в качестве определения местоположений стрелок. Теоретически примем три стрелки часов совпадающими в начале отчета времени, т. е. 12.00. Тогда в течении 12 часов совпадение часовой и минутной стрелок наступит 11 раз. Следовательно, можно вычислить и время их совмещений Тч=n*(1+1/11) в часах на циферблате, где n порядковый номер моментов совместного положения стрелок. Вычислим время первого n=1 совмещения в часах: Тч=1*(1+1/11)=1,0909. ч; в часах и минутах: Тм= 1ч+0,(09)*60 м=1ч+5,(45)м; в часах, минутах и секундах: Тс=1ч+5 м 0,(45)*60с=1ч+5м+27,(27) с. Как видим, секундная стрелка в нужный момент времени находится совсем в другом месте. Аналогичный результат и во всех других моментах времени, за исключением последнего, когда все стрелки приходят в исходное положение. Получается, теоретически можно вести речь о двух совпадениях в сутки. Практически установка стрелок на заводах или часовым мастером производится с некоторой погрешностью, пусть и малой. По этой причине три стрелки часов никогда не совпадают.

Сколько раз в день стрелки часов совпадают?

Следующий раз возможен в 0 часов 0 минут, но это уже повторение самого первого раза.

То есть всего 22 раза догоняет минутная стрелка часовую.

В день (в сутки) стрелки часов совпадают 23 раза

Сколько раз за день пересекаются стрелки часов. Сколько раз в течение суток перекрываются часовая и минутная стрелки

Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой – 1 деление/час. До четвертой встречи минутной и часовой стрелок минутная должна сначала 3 раза «обогнать» часовую, то есть пройти 3 круга по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет

делений. Тогда общий путь минутной стрелки складывается из найденных 36 делений, ещё 8 изначально разделяющих их делений (поскольку часы показывают 8 часов) и последних L делений. Приравняем время движения часовой и минутной стрелок:

Часовая стрелка пройдет 4 деления, что соответствует 4 часам, то есть 240 минутам.

Приведем другое решение.

Ясно, что в первый раз стрелки встретятся между 8 и 9 часами, второй раз — между 9 и 10 часами, третий — между 10 и 11, четвертый — между 11 и 12 часами, то есть ровно в 12 часов. Таким образом, они встретятся ровно через 4 часа, что составляет 240 минут.

По просьбам читателей помещаем общее решение.

Скорость вращения часовой стрелки равна 0,5 градуса в минуту, а минутной — 6 градусов в минуту. Поэтому когда часы показывают время h часов m минут часовая стрелка повернута на 30h + 0,5m градусов, а минутная — на 6m градусов относительно 12-часового деления.

Пусть в первый раз стрелки встретятся через t₁ минут. Тогда если минутная стрелка еще не опережала часовую в течение текущего часа, то 6m + 6t₁ = 30h + 0,5m + 0,5t₁, т. е. t₁ = (60h − 11m)/11 (*). В противоположном случае получаем уравнение 6m + 6t₁ = 30h + 0,5m + 0,5t₁ + 360, откуда t₁ = (60h − 11m + 720)/11 (**).

Пусть во второй раз стрелки встретятся через t₂ минут после первого, тогда 0,5t₂ = 6t₂ − 360, откуда t₂ = 720/11 (***). Это же верно для каждого следующего оборота.

Поэтому для встречи с номером n из (*) и (**) с учетом (***) имеем соответственно: t_n = (60h − 11m + 720(n − 1))/11 или t_n = (60h − 11m + 720n)/11.

Источники:

http://tproger.ru/problems/clock/
http://timezin.ru/stati/skolko-raz-za-sutki-strelki-chasov-sovpadayut-v-odnom-polozhenii.html
http://ege.sdamgia.ru/problem?id=99600

Задача про аналоговые часы с секундной стрелкой

Разбор головоломки по книге «Действительно ли Вы достаточно умны, чтобы работать в Google?»

Задачи со стрелками исправных часов

Попробуйте решить самостоятельно!
Если что-то не получается, не отчаивайтесь, ответ и решение расположены ниже.

1.   Сколько раз в сутки показания часов обладают тем
свойством, что, меняя местами минутную и часовую стрелки, мы придем к имеющему
смысл показанию часов?
2.   Сколько раз в сутки часовая и
минутная стрелки образуют прямой угол?
3.   Через сколько минут стрелки часов (нормальных) после
совмещения наложатся снова?
4.   Во сколько раз число, показывающее, во сколько раз
скорость секундной стрелки больше скорости минутной, больше числа,
показывающего, во сколько раз скорость минутной стрелки больше скорости часовой
стрелки?
5.    Сколько раз часовые стрелки будут находится одна над
другой в течение 12 часов?
6.   Некоторая работа была начата в пятом часу, а закончена в
восьмом часу, причем показания часов в начале и в конце работы переводятся друг
в друга, если поменять местами часовую и минутную стрелки. Определить
продолжительность работы и показать, что в начале и в конце работы стрелки были
одинаково отклонены от вертикального направления.
7.     Сколько раз в сутки минутная
стрелка обгоняет часовую? А секундная?
8.   Часы пробили полночь. Сколько раз
и в какие моменты времени до следующей полуночи часовая и минутная стрелки
будут совмещены?
9.   Между какими цифрами находится секундная стрелка в момент
первого совмещения часовой стрелки с минутной после полудня?
10.
Почему
на часах стрелки ходят слева направо (по часовой стрелке), а не наоборот?
11.   На
часах с тремя стрелками — часовой, минутной и секундной — в 12 часов все три
стрелки совпадают. Существуют ли еще другие моменты времени, когда все три
стрелки совпадают?
12.  Задача, предложенная
Льюисом Кэрроллом: какие часы точнее показывают
время: те, которые отстают на минуту в сутки, или те, которые вовсе не идут?
13. На
сколько градусов поворачивается за минуту минутная стрелка? Часовая стрелка?
14. Определите
величину угла между часовой и минутной стрелками часов, показывающими 1 час 10
минут при условии, что обе стрелки движутся с постоянными скоростями.
15. Стрелки
часов только что сошлись. Через сколько минут они будут
«смотреть» в противоположные стороны?
16.   Но вы замечали, вероятно, что это не
единственный момент, когда стрелки часов встречаются: они настигают друг друга
в течение дня несколько раз. Можете ли вы указать все те моменты, когда это
случается?
17. Когда
же произойдет следующая встреча?
18.  В 6
часов, наоборот, обе стрелки направлены в противоположные стороны. Но только ли
в 6 часов это бывает или же есть и другие моменты, когда стрелки так расположены?
19.  Я
взглянул на часы и заметил, что обе стрелки отстоят от цифры 6, по обе ее
стороны, одинаково. В котором часу это было?
20. В
котором часу минутная стрелка опережает часовую ровно на столько же, на сколько
часовая находится впереди числа 12 на циферблате? А может быть, таких моментов
бывает в день несколько или же вовсе не бывает?
21.   Какой угол образуют стрелки часов в 12 часов 20
минут?
22. Найдите
угол между часовой и минутной стрелками а) в 9 часов 15 минут;
б) в 14 часов 12 минут?
23. Когда
угол между часовой и минутной стрелками часов больше а) в 13:45 или в
22:15; б) в 13:43 или в 22:17; в) через t минут после полудня
или за t минут до полуночи?
24. Стрелки
часов только что сошлись. Через сколько минут они будут
«смотреть» в противоположные стороны?
25. Как
можно объяснить, что в исправных часах за одну секунду минутная стрелка прошла
6 минут.
26. По
точному хронометру было установлено, что часовая и минутная стрелки равномерно
идущих (но с неправильной скоростью!) часов совпадают через каждые 66 минут. На
сколько минут в час спешат или отстают эти часы?
27. В
Италии выпускают часы, в которых часовая стрелка делает в сутки один оборот, а
минутная – 24 оборота, причём, как обычно, минутная стрелка длиннее
часовой (в обычных часах часовая стрелка делает в сутки два оборота, а
минутная – 24). Рассмотрим все положения двух стрелок и нулевого деления,
которые встречаются и на итальянских часах, и на обычных. Сколько существует
таких положений? (Нулевое деление отмечает 24 часа в итальянских часах и 12
часов в обычных часах).
28. Вася
измерил транспортиром и записал в тетрадку углы между часовой и минутной
стрелками сначала в 8:20, а потом в 9:25. После этого Петя забрал свой
транспортир. Помогите Васе найти углы между стрелками в 10:30 и 11:35.
29. Сколько
раз с 12:00 до 23:59 совпадают минутная и часовая стрелки часов?
30. На
часах полдень. Когда часовая и минутная стрелки совпадут в следующий раз?
31. Укажите
хотя бы один момент времени, отличный от 6:00 и 18:00, когда часовая и минутная
стрелки правильно идущих часов направлены в противоположные стороны.
32. Когда
Петя начал решать эту задачу, он заметил, что часовая и минутная стрелки его
часов образуют прямой угол. Пока он решал ее, угол все время был тупым, а в тот
момент, когда Петя закончил решение, угол снова стал прямым. Сколько времени
Петя решал эту задачу?
33. Петя
проснулся в восьмом часу утра и заметил, что часовая стрелка его будильника
делит пополам угол между минутной стрелкой и стрелкой звонка, показывающей на
цифру 8. Через какое время должен прозвенеть будильник?
34. Коля
отправился за грибами между восемью и девятью часами утра в момент, когда
часовая и минутная стрелки его часов были совмещены. Домой он вернулся между
двумя и тремя часами дня, при этом стрелки его часов были направлены в
противоположные стороны. Сколько продолжалась Колина прогулка?
35. Ученик
начал решать задачу между 9 и 10 часами и закончил между 12 и 13 часами.
Сколько времени он решал задачу, если за это время часовая и минутная стрелки
часов поменялись местами?
36. Сколько
раз в течение суток часовая и минутная стрелки правильно идущих часов образуют
угол в 30 градусов?
37. Перед
вами часы. Сколько существует положений стрелок, по которым нельзя определить
время, если не знать, какая стрелка часовая, а какая минутная? (Считается, что
положение каждой из стрелок можно определить точно, но следить за тем, как
стрелки двигаются, нельзя.)
38. В мире
антиподов минутная стрелка часов идет с нормальной скоростью, но в
противоположную сторону. Сколько раз за сутки стрелки антиподных часов
а) совпадают; б) противоположны?
39. Сколько раз в сутки антиподные часы невозможно отличить
от нормальных (если не знать, который час на самом деле)?
40. Муха в полдень села на секундную стрелку часов и
поехала, придерживаясь следующих правил: если она обгоняет какую-то стрелку или
ее обгоняет какая-то стрелка (кроме секундной у часов есть часовая и минутная
стрелки), то муха переползает на эту стрелку. Сколько кругов проедет муха
в течение часа?

Выяснить закономерность в изменении времени на часах и определить, что должны показывать часы под номером пять.

Задания с ОГЭ

1. Какой угол (в градусах) образуют минутная и часовая
стрелки часов в 4 ч?
2.Какой угол (в градусах) описывает
минутная стрелка за 6 минут?

Задания ЕГЭ

1. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Эта задача ничуть не сложнее, чем задача на движение по кругу. У нас по кругу движутся часовая и минутная стрелки. Минутная стрелка за час проходит полный круг, то есть 360°. Значит, ее скорость равна 360° в час. Часовая стрелка за час проходит угол 30° ( это угол между двумя соседними числами на циферблате). Значит, ее скорость 30° в час.

В 8 часов 00 минут расстояние между стрелками составляет 240°:

Пусть минутная стрелка в первый раз встретится с часовой через t часов. За это время минутная стрелка пройдет 360°t, а часовая 30°t, причем минутная пройдет на 240° больше, чем часовая. Получим уравнение:

360°t-30°t=240°

t=240°/330°=8/11

То есть через 8/11 часа стрелки первый раз встретятся.

Теперь до следующей встречи минутная стрелка пройдет на 360° больше, чем часовая. Пусть это произойдет через х часов.

Получим уравнение:

360°х-30°х=360°. Отсюда х=12/11. И так еще два раза.

Получаем, что минутная стрелка в четвертый раз поравняется с часовой через 8/11+12/11+12/11+12/11= 4 часа= 240 мин.

Ответ: 240 мин.

2. Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

В этой задаче скорость движения стрелок будем выражать в градусах/минуту.

Скорость минутной стрелки равна 360˚/60=6˚ в минуту.

Скорость часовой стрелки равна 30˚/60=0,5˚ в минуту.

В 0 часов положение часовой и минутной стрелок совпадало. 1 час 35 минут — это 95 минут. За это время минутная стрелка прошла 95х6=570˚=360˚+210˚, а часовая прошла 95×0,5˚=47,5˚. И у нас такая картинка:

Первый раз стрелки встретятся через время , когда часовая стрелка повернется на , а минутная на 150˚+47,5˚ больше. Получаем уравнение для :

Отсюда

Следующий раз стрелки встретятся, когда минутная пройдет на круг больше часовой:

И так 9 раз.

Минутная стрелка в десятый раз поравняется с часовой через минут

Ответ: 625

Ответы:
1. за 12 часов 132, за 24 часа 264 момента плюс 22
наложения, итого 286

2. В сутки часовая стрелка делает 2 оборота , а минутная
— 24 . Отсюда минутная стрелка обгоняет часовую 22 раза и каждый раз с часовой
стрелкой образуется по два прямых угла, т.е. ответ — 44.

3.Нетрудно сообразить, что это случится спустя 1 час 5
5/11 минуты, то есть в 2 часа 10 10/11минуты. Следующая — спустя еще 1 час 5
5/11 минуты, то есть в 3 часа 16 4/11 минуты, и т. д. Всех встреч, как легко
видеть, будет 11; 11-я наступит через 1 1/11 —12 часов после первой, то есть в
12 часов; другими словами, она совпадает с первой встречей, и дальнейшие
встречи повторятся снова в прежние моменты.

Вот все моменты встреч:

1-я встреча  —
в  1  час         5
5/11 минуты

2-я       «    —
«2 часа         10
10/11  «

3-я       «    —
«3 часа         16
4/11    «

4-я       «    —
«4 часа         21
9/11    «

5-я       «    —
«5 часов       27
3/11    «

6-я       «    —
«6 часов       32
8/11    «

7-я       «    —
«7 часов       38
2/11    «

8-я       «    —
«8 часов       43
7/11    «

9-я       «    —
«9 часов       49
1/11    «

10-я       «     —
«10 часов      54
6/11   «

11-я « —
«12 часов

через 65,(45) мин=65 9/11 мин.

6. начало в 4 часа 36, 923 мин, конец в 7
часов 23, 076 мин, длительность 2 часа
46, 153 мин.

7. В сутки часовая стрелка делает 2 оборота, а
минутная — 24 . Отсюда минутная стрелка обгоняет часовую 22 раза.

9. 4 и 5

10. Именно так движется тень в
самых первых часах — солнечных. А затем уже механические часы скопировали
направление движения стрелок. Кстати, в Южном полушарии все наоборот — тень в
солнечных часах движется против часовой стрелки.

11. Не
существует.

12. Кэрролл считал, что точными являются
стоящие часы. Вот как он это обосновывал. Часы, отстающие на минуту в сутки,
показывают точное время один раз в два года, в то время как стоящие часы
показывают точное время два раза в сутки.

13. За час минутная
стрелка делает полный оборот. Значит, за минуту она поворачивается на¹/₆₀часть
угла в 360°, то есть на 6°. Часовая стрелка за час проходит¹/₁₂часть
круга, то есть движется в 12 раз медленнее минутной. За минуту она
поворачивается на 0,5°.

14. В 1:00 минутная стрелка
«отставала» от часовой на 30°. За 10 минут, прошедших после этого
момента, часовая стрелка «пройдёт» 5°, а минутная – 60°, поэтому угол
между ними равен 60° – 30° – 5° = 25°.

15. Пусть х − промежуток времени в минутах, который
должен пройти, прежде чем стрелки разместятся на одной прямой и будут
направлены в разные стороны. Минутная стрелка успеет пройти за это время х
минутных делений циферблата, а часовая — х/12 минутных делений. Когда
стрелки разместятся на одной прямой и будут направлены в разные стороны, их
будут разделять 30 минутных делений циферблата. А значит, в это время x –
x/12 = 30, откуда х = 32 (8/11). Через 32 (8/11) минут стрелки будут
«смотреть» в противоположные стороны.

16. Начнем
наблюдать за движением стрелок в 12 часов. В этот момент обе стрелки друг друга
покрывают. Так как часовая стрелка движется в 12 раз медленнее, чем минутная
(она описывает полный круг в 12 часов, а минутная в 1 час), то в течение
ближайшего часа стрелки, конечно, встретиться не могут. Но вот прошел час;
часовая стрелка стоит у цифры 1, сделав 1/12 долю полного оборота; минутная же
сделала полный оборот и стоит снова у 12 — на 1/12 долю круга позади часовой.
Теперь условия состязания иные, чем раньше: часовая стрелка движется медленнее
минутной, но она впереди, и минутная должна ее догнать. Если бы состязание
длилось целый час, то за это время минутная стрелка прошла бы полный круг, а
часовая 1/12 круга, то есть минутная сделала бы на 11/12 круга больше. Но,
чтобы догнать часовую стрелку, минутной нужно пройти больше, чем часовой,
только на ту 1/12 долю круга, которая их отделяет. Для этого потребуется
времени не целый час, а меньше во столько раз, во сколько раз 1/12 меньше
11/12, то есть в 11 раз. Значит, стрелки встретятся через 1/11 часа, то есть
через 60/11 = 5 5/11 минуты. Итак, встреча стрелок случится спустя 5 5/11
минуты после того, как пройдет 1 час, то есть в 5 5/11 минуты второго.

21. Ответ: Нетрудно сообразить, что это случится
спустя 1 час 5 5/11 минуты, то есть в 2 часа 10 10/11минуты. Следующая — спустя
еще 1 час 5 5/11 минуты, то есть в 3 часа 16 4/11 минуты, и т. д. Всех встреч,
как легко видеть, будет 11; 11-я наступит через 1 1/11 —12 часов после первой,
то есть в 12 часов; другими словами, она совпадает с первой встречей, и
дальнейшие встречи повторятся снова в прежние моменты.Вот все моменты встреч:

24. Пусть обе стрелки стояли у 12, и затем часовая
отошла от 12 на некоторую часть полного оборота, которую мы обозначим буквой х.
Минутная стрелка за то же время успела повернуться на 12х. Если времени
прошло не больше одного часа, то для удовлетворения требования нашей задачи
необходимо, чтобы минутная стрелка отстояла от конца целого круга на столько
же, на сколько часовая стрелка успела отойти от начала; другими словами: 1 — 12
• х = х Отсюда 1 = 13 • х. Следовательно, х = 1/13 доле целого оборота. Такую
долю оборота часовая стрелка проходит в 12/13 часа, то есть показывает 55 5/13
минуты первого. Минутная стрелка в то же время прошла в 12 раз больше, то есть
12/13 полного оборота; обе стрелки, как видите, отстоят от 12 одинаково, а
следовательно, одинаково отодвинуты и от 6 по разные стороны. Мы нашли
одно положение стрелок — именно то, которое наступает в течение первого часа. В
течение второго часа подобное положение наступит еще раз; мы найдем его,
рассуждая по предыдущему, из равенства 1— (12х — 1) = х, или 2— 12х = х, откуда
2 = 13х, и , следовательно, х = 2/13 полного оборота. В таком положении стрелки
будут в 1 11/13 часа, то есть в 50 10/13 минуты второго. В третий раз стрелки
займут требуемое положение, когда часовая стрелка отойдет от 12 на 3/13 полного
круга, то есть 2 10/13 часа, и т. д. Всех положений 11, причем после 6 часов
стрелки меняются местами: часовая стрелка занимает те места, в которых была
раньше минутная, а минутная становится на места часовой. Если вы внимательно
наблюдаете за часами, то, быть может, вам случалось наблюдать и как раз
обратное расположение стрелок, чем сейчас описано: часовая стрелка опережает
минутную на столько же, на сколько минутная продвинулась вперед от числа 12.
Когда же это бывает? Ответ: В первый раз требуемое расположение стрелок будет в
тот момент, который определяется равенством:12х — 1 = х/2, откуда 1 = 11 ½ х,
или х = 2/23 целого оборота, то есть через 1 1/23 часа после 12. Значит, в 1
час 21 4/23 минуты стрелки будут расположены требуемым образом. Действительно,
минутная стрелка должна стоять посередине между 12 и 1 1/23 часами, то есть на
12/23 часа, что как раз и составляет 1/23 полного оборота (часовая стрелка
пройдет 2/23 целого оборота). Второй раз стрелки расположатся
требуемым образом в момент, который определится из равенства: 12х —
2= х/2, откуда 2 = 11 1/2 х и х = 4/23; искомый момент — 2 часа 5 5/23
минуты.Третий искомый момент — 3 часа 7 19/23 минуты, и т. д.

40. 21 круг

Неделя математики.

Новости ГУО «Гнезновский УПК детский сад

Неделя с 13 по 18 февраля 2017 года в нашем учреждении образования посвящается МАТЕМАТИКЕ! Приглашаем всех учащихся принять активное участие в конкурсах и викторинах.

Тем, кто учит математику,

тем, кто учит математике,

тем, кто любит математику,

тем, кто ещё не знает, что может любить математику, неделя математики посвящается.

Наши конкурсы:

Конкурс «Смекалистых»

Конкурс математических газет

Конкурс математических кроссвордов

Конкурс на лучшую тетрадь по математике

Конкурс ответов на вопрос «Почему на 0 делить нельзя?»

Подготовка сообщений, сочинений и рефератов «В чем красота математики»

Конкурс рисунков (графиков, чертежей) на тему красоты математики

Викторина

«Часовой циферблат»

1. Сколько раз в сутки показания часов обладают тем свойством, что, меняя местами минутную и часовую стрелки, мы придем к имеющему смысл показанию часов?

2. Сколько раз в сутки часовая и минутная стрелки образуют прямой угол?

3. Через сколько минут стрелки часов (нормальных) после совмещения наложатся снова?

4. Во сколько раз число, показывающее, во сколько раз скорость секундной стрелки больше скорости минутной, больше числа, показывающего, во сколько раз скорость минутной стрелки больше скорости часовой стрелки?

5. Сколько раз часовые стрелки будут находится одна над другой в течение 12 часов?

6. Некоторая работа была начата в пятом часу, а закончена в восьмом часу, причем показания часов в начале и в конце работы переводятся друг в друга, если поменять местами часовую и минутную стрелки. Определить продолжительность работы и показать, что в начале и в конце работы стрелки были одинаково отклонены от вертикального направления.

7. Сколько раз в сутки минутная стрелка обгоняет часовую? А секундная?

8. Часы пробили полночь. Сколько раз и в какие моменты времени до следующей полуночи часовая и минутная стрелки будут совмещены?

9. Между какими цифрами находится секундная стрелка в момент первого совмещения часовой стрелки с минутной после полудня?

10. Почему на часах стрелки ходят слева направо (по часовой стрелке), а не наоборот?

11. На часах с тремя стрелками — часовой, минутной и секундной — в 12 часов все три стрелки совпадают. Существуют ли еще другие моменты времени, когда все три стрелки совпадают?

12. Задача, предложенная Льюисом Кэрроллом: какие часы точнее показывают время: те, которые отстают на минуту в сутки, или те, которые вовсе не идут?

13. На сколько градусов поворачивается за минуту минутная стрелка? Часовая стрелка?

14. Определите величину угла между часовой и минутной стрелками часов, показывающими 1 час 10 минут при условии, что обе стрелки движутся с постоянными скоростями.

15. Стрелки часов только что сошлись. Через сколько минут они будут «смотреть» в противоположные стороны?

16. Но вы замечали, вероятно, что это не единственный момент, когда стрелки часов встречаются: они настигают друг друга в течение дня несколько раз. Можете ли вы указать все те моменты, когда это случается?

17. Когда же произойдет следующая встреча?

18. В 6 часов, наоборот, обе стрелки направлены в противоположные стороны. Но только ли в 6 часов это бывает или же есть и другие моменты, когда стрелки так расположены?

19. Я взглянул на часы и заметил, что обе стрелки отстоят от цифры 6, по обе ее стороны, одинаково. В котором часу это было?

20. В котором часу минутная стрелка опережает часовую ровно на столько же, на сколько часовая находится впереди числа 12 на циферблате? А может быть, таких моментов бывает в день несколько или же вовсе не бывает?

21. Какой угол образуют стрелки часов в 12 часов 20 минут?

22. Найдите угол между часовой и минутной стрелками а) в 9 часов 15 минут; б) в 14 часов 12 минут?

23. Когда угол между часовой и минутной стрелками часов больше а) в 13:45 или в 22:15; б) в 13:43 или в 22:17; в) через t минут после полудня или за t минут до полуночи?

24. Стрелки часов только что сошлись. Через сколько минут они будут «смотреть» в противоположные стороны?

25. Как можно объяснить, что в исправных часах за одну секунду минутная стрелка прошла 6 минут.

26. По точному хронометру было установлено, что часовая и минутная стрелки равномерно идущих (но с неправильной скоростью!) часов совпадают через каждые 66 минут. На сколько минут в час спешат или отстают эти часы?

27. В Италии выпускают часы, в которых часовая стрелка делает в сутки один оборот, а минутная – 24 оборота, причём, как обычно, минутная стрелка длиннее часовой (в обычных часах часовая стрелка делает в сутки два оборота, а минутная – 24). Рассмотрим все положения двух стрелок и нулевого деления, которые встречаются и на итальянских часах, и на обычных. Сколько существует таких положений? (Нулевое деление отмечает 24 часа в итальянских часах и 12 часов в обычных часах).

28. Вася измерил транспортиром и записал в тетрадку углы между часовой и минутной стрелками сначала в 8:20, а потом в 9:25. После этого Петя забрал свой транспортир. Помогите Васе найти углы между стрелками в 10:30 и 11:35.

29. Сколько раз с 12:00 до 23:59 совпадают минутная и часовая стрелки часов?

30. На часах полдень. Когда часовая и минутная стрелки совпадут в следующий раз?

31. Укажите хотя бы один момент времени, отличный от 6:00 и 18:00, когда часовая и минутная стрелки правильно идущих часов направлены в противоположные стороны.

32. Когда Петя начал решать эту задачу, он заметил, что часовая и минутная стрелки его часов образуют прямой угол. Пока он решал ее, угол все время был тупым, а в тот момент, когда Петя закончил решение, угол снова стал прямым. Сколько времени Петя решал эту задачу?

33. Петя проснулся в восьмом часу утра и заметил, что часовая стрелка его будильника делит пополам угол между минутной стрелкой и стрелкой звонка, показывающей на цифру 8. Через какое время должен прозвенеть будильник?

34. Коля отправился за грибами между восемью и девятью часами утра в момент, когда часовая и минутная стрелки его часов были совмещены. Домой он вернулся между двумя и тремя часами дня, при этом стрелки его часов были направлены в противоположные стороны. Сколько продолжалась Колина прогулка?

35. Ученик начал решать задачу между 9 и 10 часами и закончил между 12 и 13 часами. Сколько времени он решал задачу, если за это время часовая и минутная стрелки часов поменялись местами?

36. Сколько раз в течение суток часовая и минутная стрелки правильно идущих часов образуют угол в 30 градусов?

37. Перед вами часы. Сколько существует положений стрелок, по которым нельзя определить время, если не знать, какая стрелка часовая, а какая минутная? (Считается, что положение каждой из стрелок можно определить точно, но следить за тем, как стрелки двигаются, нельзя.)

38. В мире антиподов минутная стрелка часов идет с нормальной скоростью, но в противоположную сторону. Сколько раз за сутки стрелки антиподных часов а) совпадают; б) противоположны?

39. Сколько раз в сутки антиподные часы невозможно отличить от нормальных (если не знать, который час на самом деле)?

40. Муха в полдень села на секундную стрелку часов и поехала, придерживаясь следующих правил: если она обгоняет какую-то стрелку или ее обгоняет какая-то стрелка (кроме секундной у часов есть часовая и минутная стрелки), то муха переползает на эту стрелку. Сколько кругов проедет муха в течение часа?

Ответы (с решениями, доказательствами и поясняющими схемами) на викторину приносить учителю математики!

Сколько раз за сутки стрелки часов совпадают в одном положении

Главная » Статьи » Сколько раз за сутки стрелки часов совпадают в одном положении

Сколько раз в день стрелки часов совпадают?

Сколько раз в день стрелки часов совпадают?

Часовая стрелка за сутки два раза обходит циферблат часов, а минутная стрелка совершает 24 оборота и 22 раза догоняет часовую. Если взять за время старта время полночи, то 0 часов 0 минут, то минутная сразу убежит вперд и догонит часовую в 1 час 5 минут. Потом в 2 часа 11 минут, затем в 3 часа 16 минут, в 4 часа 22 минуты, в 5 часов 27 минут, в 6 часов 33 минуты, в 7 часов 38 минут, в 8 часов 44 минуты, в 9 часов 49 минут, в 10 часов 55 минут, в 12 часов 00 минут первый круг закончится, стрелки опять вместе и вс начнтся заново. Догонит минутная стрелка часовую в 13 часов 05 минут, в 14 часов 11 минут, в 15 часов 16 минут, в 16 часов 22 минуты, в 17 часов 27 минут, в 18 часов 33 минуты, в 19 часов 38 минут, в 20 часов 44 минуты, в 21 час 49 минут и последний раз стрелки будут вместе в 22 часа 55 минут.

Следующий раз возможен в 0 часов 0 минут, но это уже повторение самого первого раза.
То есть всего 22 раза догоняет минутная стрелка часовую.
1 раз в 00:00
2 раз в 01:05
3 раз в 02:11
4 раз в 03:16
5 раз в 04:22
6 раз в 05:27
7 раз в 06:33
8 раз в 07:38
9 раз в 08:43
10 раз в 09:49
11 раз в 10:54
12 раз в 12:00
13 раз в 13:05
14 раз в 14:11
15 раз в 15:16
16 раз в 16:22
17 раз в 17:27
18 раз в 18:33
19 раз в 19:38
20 раз в 20:43
21 раз в 21:49
22 раз в 22:54
23 раз 24:00
Это абсолютно точно (насколько это возможно высчитать, имея в руках старые карманные часы).
Если считать по картинке, то получается совпадений 24 раза. А если взять механические часы и вращать стрелки и при этом подсчитывать, сколько раз стрелки совмещаются, то получается 23 раза. Именно 23, а не 22 и не 24. Так как, сутки начинаются в 00:00 и заканчиваются в 00:00.
Насколько мне известно, в течение одних суток часовая и минутная стрелки часов в общей сложности совпадают 22 раза. Вс дело в том, что часовая и минутная стрелки часов совпадают не один раз в час, а немного реже.
Могу сказать однозначно, что стрелки часов совпадают на циферблате в сутки ровно двадцать четыре раза. Например, в 00.00, а также в 13.05 и 1.05, 14.10 и 2.10, 15.15 и 3.15, 16.20 и 4.20 и так далее, попробуйте сами посчитать.
Я думаю, что стрелки совпадают ровно 24 раза в сутки, по одному разу в каждый час. Вот, например, сейчас 12 часов ровно — стрелки совпали. 1 час 5 минут — стрелки совпали. 2 часа 10 минут — стрелки совпали и так далее.
Минутная и часовая стрелки пересекаются не раз в час, а чуть реже. К примеру, от нуля часов до 1 часа 5 минут проходит не один час, а 65 минут, и так далее. Поэтому получается цифра 11 раз за пол-суток и 22 раза за сутки. Так что, 22 пересечения, именно это окончательная цифра.
В сутки стрелки часов совпадают 22 раза.
Если взять десять суток — 220 раз.
Zmiter ответил почти точно, но если 00:00 это начало новых суток. то они заканчиваются в 23:59:59 и начинаются новые сутки. Правильный ответ 22 раза.
Стрелки часов совпадают столько раз, сколько часов есть в сутках. То есть 24 раза. Если хотите проверить и под рукой у Вас нету часов, то попробуйте воспользоваться картинкой ниже
Но точное время совпадения я сказать не смогу (только в 00-00 и 12-00), так как надо расчитывать скорость движения часовой стрелки.

info-4all.ru

Сколько Раз В Сутки Три Стрелки Часов Совпадают?

Ответы на поставленный вопрос носят в основном декларативный характер, но не как решение математической задачи. Правильный ответ, возможно, многим покажется неожиданным. Попробуем разобраться в проблеме, не прибегая к сложным приемам. Ясно, что стрелки в определенные периоды времени совпадают. Минутная обгоняет часовую, а секундная, в свою очередь, две ранее названные стрелки. Но речь ведется об одновременном совпадении трех стрелок. Следовательно, достаточно вычислить моменты совмещения минутной и часовой стрелок и определить, где будет находиться в это время секундная стрелка. Циферблат разделен на 12 часов и 60 делений (минут, секунд), которые и будем использовать в качестве определения местоположений стрелок. Теоретически примем три стрелки часов совпадающими в начале отчета времени, т. е. 12.00. Тогда в течении 12 часов совпадение часовой и минутной стрелок наступит 11 раз. Следовательно, можно вычислить и время их совмещений Тч=n*(1+1/11) в часах на циферблате, где n порядковый номер моментов совместного положения стрелок. Вычислим время первого n=1 совмещения в часах: Тч=1*(1+1/11)=1,0909. 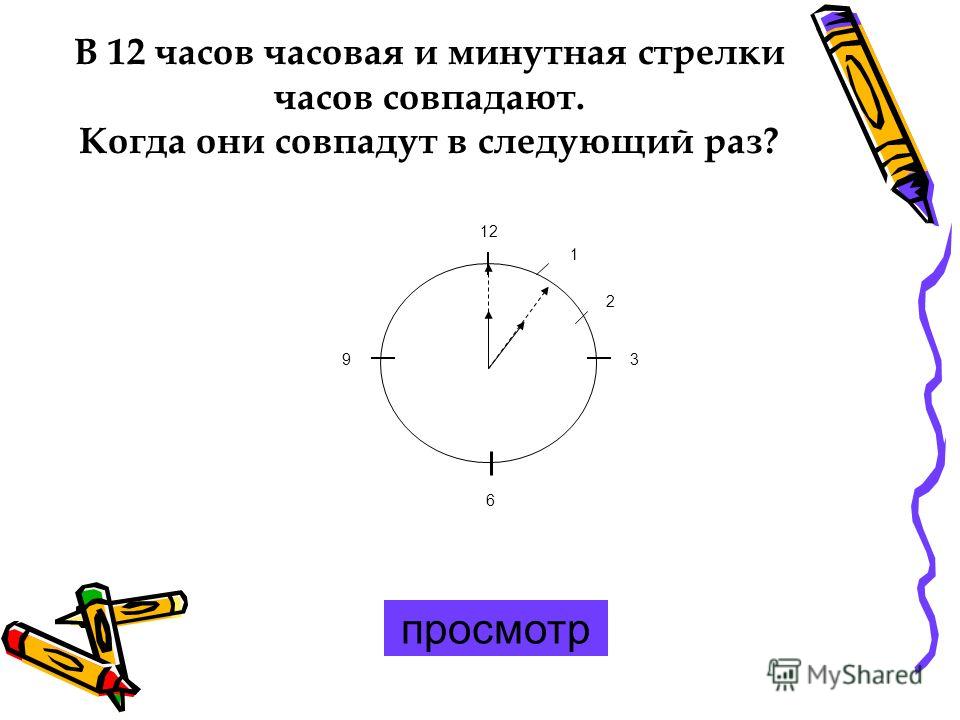..ч; в часах и минутах: Тм= 1ч+0,(09)*60 м=1ч+5,(45)м; в часах, минутах и секундах: Тс=1ч+5 м 0,(45)*60с=1ч+5м+27,(27) с. Как видим, секундная стрелка в нужный момент времени находится совсем в другом месте. Аналогичный результат и во всех других моментах времени, за исключением последнего, когда все стрелки приходят в исходное положение. Получается, теоретически можно вести речь о двух совпадениях в сутки. Практически установка стрелок на заводах или часовым мастером производится с некоторой погрешностью, пусть и малой. По этой причине три стрелки часов никогда не совпадают.

otvet.expert

Сколько раз в день стрелки часов совпадают?

Сколько раз в день стрелки часов совпадают?

Часовая стрелка за сутки два раза обходит циферблат часов, а минутная стрелка совершает 24 оборота и 22 раза догоняет часовую. Если взять за время старта время полночи, то 0 часов 0 минут, то минутная сразу убежит вперд и догонит часовую в 1 час 5 минут. Потом в 2 часа 11 минут, затем в 3 часа 16 минут, в 4 часа 22 минуты, в 5 часов 27 минут, в 6 часов 33 минуты, в 7 часов 38 минут, в 8 часов 44 минуты, в 9 часов 49 минут, в 10 часов 55 минут, в 12 часов 00 минут первый круг закончится, стрелки опять вместе и вс начнтся заново. Догонит минутная стрелка часовую в 13 часов 05 минут, в 14 часов 11 минут, в 15 часов 16 минут, в 16 часов 22 минуты, в 17 часов 27 минут, в 18 часов 33 минуты, в 19 часов 38 минут, в 20 часов 44 минуты, в 21 час 49 минут и последний раз стрелки будут вместе в 22 часа 55 минут.
Следующий раз возможен в 0 часов 0 минут, но это уже повторение самого первого раза.
То есть всего 22 раза догоняет минутная стрелка часовую.
В день (в сутки) стрелки часов совпадают 23 раза
1 раз в 00:00
2 раз в 01:05
3 раз в 02:11
4 раз в 03:16
5 раз в 04:22
6 раз в 05:27
7 раз в 06:33
8 раз в 07:38
9 раз в 08:43
10 раз в 09:49
11 раз в 10:54
12 раз в 12:00
13 раз в 13:05
14 раз в 14:11
15 раз в 15:16
16 раз в 16:22
17 раз в 17:27
18 раз в 18:33
19 раз в 19:38
20 раз в 20:43
21 раз в 21:49
22 раз в 22:54
23 раз 24:00
Это абсолютно точно (насколько это возможно высчитать, имея в руках старые карманные часы).
Если считать по картинке, то получается совпадений 24 раза. А если взять механические часы и вращать стрелки и при этом подсчитывать, сколько раз стрелки совмещаются, то получается 23 раза. Именно 23, а не 22 и не 24. Так как, сутки начинаются в 00:00 и заканчиваются в 00:00.
Насколько мне известно, в течение одних суток часовая и минутная стрелки часов в общей сложности совпадают 22 раза. Вс дело в том, что часовая и минутная стрелки часов совпадают не один раз в час, а немного реже.
Могу сказать однозначно, что стрелки часов совпадают на циферблате в сутки ровно двадцать четыре раза. Например, в 00.00, а также в 13.05 и 1.05, 14.10 и 2.10, 15.15 и 3.15, 16.20 и 4.20 и так далее, попробуйте сами посчитать.
Я думаю, что стрелки совпадают ровно 24 раза в сутки, по одному разу в каждый час. Вот, например, сейчас 12 часов ровно — стрелки совпали. 1 час 5 минут — стрелки совпали. 2 часа 10 минут — стрелки совпали и так далее.
Минутная и часовая стрелки пересекаются не раз в час, а чуть реже. К примеру, от нуля часов до 1 часа 5 минут проходит не один час, а 65 минут, и так далее. Поэтому получается цифра 11 раз за пол-суток и 22 раза за сутки. Так что, 22 пересечения, именно это окончательная цифра.
В сутки стрелки часов совпадают 22 раза.
Если взять десять суток — 220 раз.
Zmiter ответил почти точно, но если 00:00 это начало новых суток. то они заканчиваются в 23:59:59 и начинаются новые сутки. Правильный ответ 22 раза.
Стрелки часов совпадают столько раз, сколько часов есть в сутках. То есть 24 раза. Если хотите проверить и под рукой у Вас нету часов, то попробуйте воспользоваться картинкой ниже
Но точное время совпадения я сказать не смогу (только в 00-00 и 12-00), так как надо расчитывать скорость движения часовой стрелки.

woprosi.ru

Сколько раз за день минутная стрелка. Сколько раз за сутки стрелки часов совпадают в одном положении

info-4all.ru

Сколько Раз В Сутки Три Стрелки Часов Совпадают?

Ответы на поставленный вопрос носят в основном декларативный характер, но не как решение математической задачи. Правильный ответ, возможно, многим покажется неожиданным. Попробуем разобраться в проблеме, не прибегая к сложным приемам. Ясно, что стрелки в определенные периоды времени совпадают. Минутная обгоняет часовую, а секундная, в свою очередь, две ранее названные стрелки. Но речь ведется об одновременном совпадении трех стрелок. Следовательно, достаточно вычислить моменты совмещения минутной и часовой стрелок и определить, где будет находиться в это время секундная стрелка. Циферблат разделен на 12 часов и 60 делений (минут, секунд), которые и будем использовать в качестве определения местоположений стрелок. Теоретически примем три стрелки часов совпадающими в начале отчета времени, т. е. 12.00. Тогда в течении 12 часов совпадение часовой и минутной стрелок наступит 11 раз. Следовательно, можно вычислить и время их совмещений Тч=n*(1+1/11) в часах на циферблате, где n порядковый номер моментов совместного положения стрелок. Вычислим время первого n=1 совмещения в часах: Тч=1*(1+1/11)=1,0909. ..ч; в часах и минутах: Тм= 1ч+0,(09)*60 м=1ч+5,(45)м; в часах, минутах и секундах: Тс=1ч+5 м 0,(45)*60с=1ч+5м+27,(27) с. Как видим, секундная стрелка в нужный момент времени находится совсем в другом месте. Аналогичный результат и во всех других моментах времени, за исключением последнего, когда все стрелки приходят в исходное положение. Получается, теоретически можно вести речь о двух совпадениях в сутки. Практически установка стрелок на заводах или часовым мастером производится с некоторой погрешностью, пусть и малой. По этой причине три стрелки часов никогда не совпадают.

otvet.expert

Сколько раз в день стрелки часов совпадают?

Сколько раз в день стрелки часов совпадают?

Большинство людей сразу же понимает, что ответ должен быть 24 плюс-минус. Все проблема как раз в том, чтобы вычислить этот плюс-минус.
Сначала обратите внимание, что перекрытие стрелок — это абсолютно предсказуемое явление. Обе стрелки движутся с постоянной скоростью, следовательно, интервал времени между двумя последовательными перекрытиями постоянный.
Этот постоянный интервал чуть более часа. В полночь часовая и минутная стрелки точно совпадают. Минутной стрелке требуется ровно шестьдесят минут, чтобы описать полный круг, за то же самое время часовая стрелка проходит 1/12 часть круга и находится на отметке 1 час. Чтобы добраться до отметки 1 час, минутной стрелке потребуется пять минут, но за это время часовая стрелка еще немного продвинется вперед…
Перед тем как увлечься обсуждением парадокса Зенона, давайте пока предположим, что между последовательными перекрытиями стрелок проходит чуть больше, чем 65 минут. Мы также знаем, что если умножить этот точный интервал на неизвестное целое число, должно получиться ровно двадцать четыре числа, так как каждые двадцать четыре часа часовая и минутная стрелки точно перекрываются на отметке 12. На самом деле это происходит каждые двенадцать часов — ведь путь, который стрелки проходят с полуночи до полудня, точно совпадает с путем, который они проходят с полудня до полуночи.
Давайте подробно проанализируем, что происходит за двенадцать часов с полуночи до полудня. За этот период стрелки не могут совпасть двенадцать раз — в этом случае интервал между совпадениями стрелок был бы 12/12 — или ровно один час, а мы знаем, что на самом деле он чуть больше, чем 65 минут. Следовательно, за этот период стрелки могут совпасть лишь 11 раз. Это значит, что продолжительность интервала между перекрытиями стрелок 12/11, или 65,45 минуты. Это и должен быть точный интервал, который мы не смогли вычислить чуть ранее. Умножив одиннадцать на два, мы получаем двадцать два перекрытия стрелок за двадцать четыре часа. Таким образом, двадцать два — это точный ответ, если только вы не захотите учитывать и совпадение стрелок в начале суток в полночь и в конце суток в
следующую полночь — в этом случае ответом будет двадцать три.
У Майка и Тодда есть 21 доллар на двоих. У Майка на 20 долларов больше, чем у
Тодда. Сколько денег у каждого? В ответе нельзя использовать дроби.
Это вопрос с подвохом, в котором скрыт «вызов». Ответ на основной вопрос достаточно прост. У вас может возникнуть искушение ответить, что у Майка 21 доллар, а у Тодда — 1 доллар, но тогда получается сумма в 22 доллара. Правильный ответ должен быть таким: у Майка 20,50 доллара, а у Тодда — 0,50 доллара. Если это для вас не очевидно — вы можете
использовать алгебру, составить и решить уравнение. Вы также можете доказать, что это — единственный правильный ответ, но интервьюер настаивает, что в ответе нельзя использовать дроби.
Интервьюер не прав (или использует «техническую тонкость»: мол, целое количество центов — это не дроби). Ожидается, что вы будете отстаивать свою точку зрения и доказывать, что правильный ответ именно $20,50/$0,50. Такова жизнь в больших организациях.
Сколько в среднем раз вам нужно открыть наугад телефонный справочник Манхэттена, чтобы найти нужный вам номер телефона?
«Открыть наугад» подразумевает, что вы случайно открываете двухстраничный разворот книги (вы не должны пытаться использовать знания о том, какой букве алфавита соответствует нужный вам номер телефона). Подразумевается также, что, если нужный вам номер есть где бы то ни было на двух случайно открытых вами страницах, вы его обязательно найдете.
Есть и простой ответ, и более изощренный.
Вот простой ответ. Допустим, в телефонном справочнике Манхэттена одна тысяча страниц (это достаточно точная оценка: в издании этого справочника 2001 года было 1138 страниц. Вы можете игнорировать тот факт, что в начале и конце телефонной книги есть страницы, на которых нет номеров телефонов). Это значит, что в телефонной книге 500 разворотов. Таким образом, вероятность, что книга откроется в нужном вам месте в первый и в любой последующий раз, — один из пятисот.
Этот быстрый ответ вполне приемлем, учитывая, что самый уязвимый пункт в ваших рассуждениях — это догадка о количестве страниц в телефонном справочнике.
А теперь ответ, удовлетворяющий людей из «математического лагеря». В реалистической ситуации вам, наверное, захотелось бы узнать, сколько раз вам нужно случайным образом раскрыть телефонную книгу, чтобы быть уверенным с заданной вероятностью, что хотя бы один раз она раскроется на нужной вам странице. Допустим, вы хотите быть уверенными, что в 90 процентах случаев отыщете нужный вам номер. Сколько раз для этого нужно раскрыть телефонный справочник?
Поскольку это случайная процедура, абсолютных гарантий нет. Вам может повезти, и тогда вы найдете нужный номер на первой же странице, и, наоборот, вы можете миллион раз перелистывать книгу и ни разу не открыть ее на нужной странице. Если вы хотите быть на 100 процентов уверенными, то ответ прост: сколько бы раз вы ни открывали случайным образом телефонную книгу, вы никогда не можете быть уверены на 100 процентов, что она хотя бы раз откроется на нужной странице.
В общем, вам придется снова и снова раскрывать справочник, пока он открывается на ненужных вам страницах. Поэтому мы можем анализировать вероятность того, что телефонная книга будет раз за разом раскрываться на ненужных страницах.
Допустим, вам известно, что в справочнике точно 1000 страниц и 500 разворотов. Вероятность того, что вы раскроете книгу на неправильной странице в каждой из попыток — 499 из 500, так как из 500 возможных разворотов книги только один подходящий. Тогда вероятность того, что в n последовательных попытках телефонная книга каждый раз будет раскрываться на неверных страницах — (499/500)n .
Очевидно, что вероятность того, что вы откроете книгу на нужной странице за n последовательных попыток или раньше, будет равна выражению: 1-(499/500)n .
Эта формула позволяет вам вычислить, сколько раз вам нужно случайным образом раскрыть телефонную книгу, чтобы она с заданной вероятностью раскрылась на нужной вам
странице. Если вы сделаете расчеты, например в Excel, то увидите, что для 50-процентной уверенности вам нужно раскрыть телефонный справочник 347 раз (или меньше, если вам повезет). Это число попытки и можно назвать «средним».
С другой стороны, этот ответ можно считать оптимистическим. Если вы сделаете 347 попыток — шансы на успех будут только 50 на 50.
Первоначальная оценка, которая была получена при помощи простого метода, — 500 попыток дают вероятность успеха 63 процента. Для того чтобы достигнуть 90-процентной вероятности успеха, вам нужно случайным образом раскрыть книгу 1150 раз.
Как можно разрезать прямоугольный торт на два равных куска, если кто-то уже вырезал из него прямоугольный кусок?..
Есть два правильных ответа, и лучше, если вы дадите их оба. Более простой ответ находят реже, чем сложный.
Можно очень легко разрезать прямоугольник пополам — вам нужно только позаботиться
о том, чтобы разрез прошел через его центр, причем под любым углом.
В данном случае у нас два прямоугольника: «позитивный» (то, что пока осталось от торта) и «негативный» (недостающий кусок). Найдите центры обоих прямоугольников и проведите через них прямую линию — это и будет линия разреза. Вы получите два равных куска.

Рдирез, проходя щий через центры двух прямоугольников

А л ьтерк атн ни м » решение

Поскольку разрез проходит через центры обоих прямоугольников, площадь двух кусков будет такова: половина площади торта минус половина площади вырезанного из торта куска. Другими словами, площадь двух кусков будет одинаковой. Это будет верным, несмотря на то, что форма кусков может быть различной.
В маловероятном случае, когда центры обоих прямоугольников оказались в одной и той же точке, можно делать разрез в любом направлении, но он, конечно, должен проходить через центр.
Альтернативное решение — резать торт не вертикально, а горизонтально, чтобы получить куски, толщина которых будет в два раза меньше, чем у целого торта, и в каждом не будет хватать одинакового по форме и площади куска. Это решение, конечно, не подходит, если торт сверху покрыт глазурью.
Какой дизайн вы предложите для туалетной комнаты Билла Гейтса?
Для ответа наэтот вопрос нужно учесть два важных обстоятельства. Во-первых, Билл Гейтс всегда может позволить себе получить то, что хочет. Во-вторых, вы должны по крайней мере предложить какие-то идеи, которые могут понравиться Гейтсу, хотя он сам об этом пока

не задумывался (иначе какой смысл нанимать вас для дизайна его туалетной комнаты?).
Подразумевается, что вы усядетесь где-то вместе с Гейтсом и выслушаете, какой бы он хотел видеть свою туалетную комнату. Он сообщит вам о бюджете и сроках. Вы предложите ему много разных идей и узнаете его мнение о них. Потом вы составите план и подадите его на утверждение Гейтсу. Этот план придется не раз пересматривать, а вы, несмотря на это, должны позаботиться о том, чтобы проект уложился в срок и бюджет не был превышен. Это относится к любой задаче на разработку дизайна.
Что касается конкретных идей, которые вы предложите, имейте в виду, что вам будет трудно превзойти то, что у Гейтса уже есть в реальности. Ванная Билла Гейтса устроена так, что он может, не выходя из машины, послать команду и заполнить ее водой нужной температуры. На самом деле!
Компьютеризировать весь свой дом — это идея, к которой люди из Microsoft относятся очень серьезно. Исследовательские подразделения Microsoft разрабатывают «умные» шкафчики для лекарств и туалетных принадлежностей, которые сообщат вам, что у вас заканчивается нужное вам лекарство или туалетная бумага. «Некоторые из этих „сценариев будущего“ могут показаться очень странными, признает Тед Куммер, вице-президент Microsoft по программе MSN Internet Access. — Ну, например, унитаз, который следит за здоровьем всех членов семьи, делая регулярные химические анализы, шкафчик для лекарств, который помогает заказать номер в гостинице или запереть вашу машину в гараже».
Поэтому, если вы хотите удивить интервьюеров из Microsoft, вам вряд ли удастся это сделать, рассуждая об унитазах с электрическим подогревом. Вот несколько идей, которые им могут понравиться (это идеи футуристические, но уже сегодня их могут позволить себе богатые потребители, для которых деньги — не вопрос). Устройство, которое автоматически запирает шкафчики с лекарствами или средствами бытовой химии, когда в ванную входит ребенок без присмотра взрослых. В доме Гейтса уже можно отслеживать, кто находится в той или иной комнате. Идет разговор о сканировании радужной оболочки глаза и других способах быстрой и незаметной идентификации людей. Это как раз и может помочь запирать шкафчик с лекарствами от детей, «если это позволит спасти жизнь хотя бы одному ребенку», и т. д. и т. п. Блокнот для заметок, к которому не нужно прикасаться руками. Каждому человеку иногда приходят в голову хорошие идеи, когда он находится в туалете. Вам не захочется прикасаться к своей электронной записной книжке-«наладоннику» мокрыми руками, и если в доме Гейтса и есть такая комната, где нет компьютера, так это, наверное, туалет. Все, что вам нужно, — это устройство распознавания голоса, которое сможет записать ваше сообщение после того, как вы произнесете кодовую фразу, например «Заметки для Билла». Это устройство может автоматически отсылать записанную информацию по электронной почте к вам на работу. Зеркало, которое не меняет местами право и лево. Это видеоэкран и скрытая видеокамера, которые будут показывать ваше изображение таким, каким его видят другие люди, глядящие на вас. Вам будет гораздо легче пользоваться ножницами, чтобы, например, отстричь выросший не на месте волосок или подравнять усы. Если вы думаете, что эти незначительные преимущества вряд ли оправдывают отказ от «низкотехнологичного» решения, которое работает безотказно, не нуждается в новом программном обеспечении и будет работать, даже если отключится электричество… Ну, вы уверены, что

действительно хотите работать в Microsoft! (У Гейтса была идея, что репродукции
произведений искусства на жидкокристаллических экранах, которые вы увидите повсюду в его доме, если на них никто не смотрит, должны сливаться с деревянной отделкой стен, имитируя и фактуру дерева. Этого так и не удалось добиться. Все закончилось тем, что Гейтс заказал у столяров скользящие деревянные панели, которые могут закрывать видеоэкраны.)
Другие компании — производители программного обеспечения стали также задавать кандидатам на работу вопрос о туалетной комнате. Они, правда, часто варьируют пол и физические размеры главного героя: «Какой дизайн вы предложите для туалетной комнаты, которой будет пользоваться богатая дама, весящая сто пятьдесят килограммов?»
Как вы сконструируете микроволновую печь, управляемую компьютером?
Легко понять, что микроволновая печь и компьютер — не самая великая пара, которая может стать наследницей великих танцовщиков Фреда Астера и Джинджер Робертс. Многие вопросы о дизайне именно таковы: вам дают какую-нибудь сомнительную идею и просят на ее основе сконструировать что-нибудь по возможности не очень глупое.
Микроволновыми печками теперь довольно просто управлять. Пользователям, наверное, не понравятся новшества, которые усложнят управление (но вам стоит сказать, что вы проведете исследование мнений потребителей для проверки — это почти всегда ожидается, когда вам зададут вопрос о дизайне). По ряду намеков интервьюеров Microsoft можно понять, что они имеют в виду «умную упаковку»: на бытовых приборах и кухонной мебели можно установить сенсоры, которые будут считывать информацию со специальных ярлыков и штрих-кодов, помещенных на упаковке продуктов. Если речь идет о микроволновке — вы можете положить в нее замороженную лазанью, а она сама «прочтет» код с инструкциями по размораживанию (или загрузит их из Интернета). Она также автоматически установит мощность и сделает нужные поправки (учтет размер упаковки, температуру полуфабриката и т.п.). Вам уже никогда не понадобится вручную устанавливать время и другие параметры.
«Умная» упаковка позволит микроволновке хранить данные обо всей приготовленной еде. Это важно упомянуть, потому что анализ информации об использовании бытовых приборов в маркетинговых целях сейчас — популярная идея в Microsoft. С точки зрения потребителя, такой архив информации может быть полезен, чтобы планировать, какую еду нужно покупать на неделе, и учитывать количество съеденных калорий, если потребитель на диете.
Еще один хороший ответ — сказать, что программа распознавания голоса может сделать ненужными кнопки на микроволновке. Вместо того чтобы нажимать на них, вы сможете просто сказать вашей микроволновой печке, как долго она должна готовить какие-то продукты (допустим, овощи или рыбу — любые другие продукты, на которых нет кодовой информации), или вы можете сообщить микроволновке, что вы собираетесь готовить, а она сама определит, сколько времени это нужно готовить.
Какой дизайн вы предложите для пульта управления видеомагнитофоном?
Десятки талантливых промышленных дизайнеров работали над этой проблемой. Вряд ли вам удастся за пятнадцать минут их превзойти. Интервьюер и не ожидает от вас этого. Лучший способ начать ответ — показать, что вы понимаете, что есть несколько важных противоречий, которые необходимо учесть в дизайне. Вот два наиболее значимых.

которые не знают, как запрограммировать свои видеомагнитофоны, чем по поводу ужасной
еды, которую дают в самолетах (или ее фактического отсутствия) . Но действительно ли мы хотим платить за что-то более привлекательное? Большинство людей покупает самый дешевый билет на самолет, а потом жалуется на плохое качество еды. Авиакомпании знают об этом, вот почему вы в лучшем случае получите от них горсточку пережаренного арахиса. Вполне возможно, что это верно и для рынка видеомагнитофонов. Люди покупают прежде всего из-за цены и меньше внимания обращают на качество, а потом жалуются, что пультом управления трудно пользоваться.
Сколько точно есть людей, готовых платить дополнительно за удобные пульты дистанционного управления видеомагнитофонами? Если это в основном богатые пенсионеры, у которых проблемы со зрением, — это одна история. А если это в первую очередь восьмилетние дети, у которых есть свой телевизор, и они хотели бы иметь еще и собственный недорогой видеомагнитофон — дизайн, очевидно, должен быть другим. А вот если окажется, что никто не хочет платить за более удобный в использовании пульт управления — это значит, что нужно вообще отказаться от этой идеи.
2. Легкость использования или дополнительные возможности. Вы можете сконструировать видеомагнитофон, который будет управляться при помощи всего одной кнопки. Вы нажимаете на эту кнопку и начинается запись, нажимаете на нее еще раз — запись останавливается. Вот он, видеомагнитофон, которым любому будет легко управлять.
Дополнительные функции нужны только в том случае, если вы хотите, чтобы видеомагнитофон записывал телепередачи, когда вас нет дома, чтобы их потом можно было просматривать. Маловероятно, что все захотят купить видеомагнитофон всего с одной кнопкой управления только потому, что им легко управлять. Сегодняшние производители снабжают видеомагнитофоны большим набором функций, которыми можно управлять при помощи пульта управления переключая его в нужный режим. Вы не можете просто ввести с помощью клавиатуры или выбрать время, когда видеомагнитофон должен начать запись — вместо этого вам придется долго нажимать на кнопки, устанавливая количество минут, часов, время до или после полудня, день, неделю. Это затрудняет программирование видеомагнитофона.
Чтобы упростить задачу, предположим, что маркетинговые исследования показали, что есть потребители, заинтересованные в покупке более легких в управлении видеомагнитофонов. Будет также полезно узнать, пользуются ли эти потенциальные покупатели всем набором функций, которыми обладает большинство современных видеомагнитофонов. Как часто обладатели видеомагнитофонов программируют их для записи за неделю до того, как программа появится в эфире? За двадцать четыре часа до показа? Если отказаться от некоторых функций, это может упростить интерфейс.
Вот грубый набросок того, как мог бы работать такой простой и удобный интерфейс: на корпусе видеомагнитофона всего пять кнопок (воспроизведение, пауза, прямая перемотка, обратная перемотка и смена кассеты). Это на самом деле только резервный пульт управления, на тот случай, если дистанционный пульт куда-нибудь «завалится». На корпусе видеомагнитофона не будет дисплея (в целях экономии). Все программирование выполняется при помощи дистанционного пульта и экранных меню. На пульте дистанционного управления только одна кнопка и «джойстик». Джойстик будет похож на устройства, которыми снабжаются некоторые ноутбуки и компьютерные мониторы. Они тоже похожи на кнопку, которую вы можете двигать в любом направлении, чтобы контролировать перемещающийся по экрану курсор. Кнопка на пульте — для выбора функций. По существу этот пульт — аналог компьютерной мыши.

Чтобы запрограммировать ваш магнитофон, вы берете пульт и нажимаете джойстик или кнопку. Это «пробуждает» видеомагнитофон (если он в данный момент не работает), и на экране телевизора появляется меню/помощник/панель управления. Такой интерфейс позволяет проигрывать записанные кассеты, записывать программы и устанавливать нужное время (если по какой-то причине вас не удовлетворяет автоматическая синхронизация). Видеомагнитофон будет загружать и показывать на экране телепрограмму, и вы будете просто выбирать нужные вам передачи и щелкать кнопкой пульта, чтобы они были записаны.
Поскольку основным маркетинговым преимуществом такого дизайна должна быть простота двухкнопочного управления, повышенное внимание нужно уделить внешнему виду пульта, его декоративному дизайну и приятным ощущениям при пользовании им. Он не должен быть похож на другие пульты. Если ваша целевая группа — молодые люди, он должен выглядеть «круто», например, как прозрачный компьютер iMac фирмы Apple. Если же основная целевая группа — пенсионеры, позаботьтесь о том, чтобы пульт и кнопки были удобными для тех, у кого пальцы уже не обладают былой подвижностью.
Разработайте дизайн пульта управления для подъемных жалюзи.
У обычных жалюзи два «устройства» для управления (обычно это просто два шнура) — одно их поднимает и опускает, а другое изменяет угол, под которым повернуты планки. Таким образом, пульт должен управлять этими двумя параметрами, возможно, при помощи двух кулисных переключателей.
Как только вы установите механизм для открывания и закрывания жалюзи, вы можете добавить функцию, позволяющую программировать эти процессы. Люди обычно не открывают и не закрывают жалюзи без причин. Они а) открывают их, чтобы было больше света; b) закрывают, когда солнце светит кому-то прямо в глаза или ковер может выцвести; с) закрывают их ночью, чтобы никто не подглядывал в окна.
Здесь нужно проанализировать то же противоречие между легкостью использования и разнообразием функций, что и в случае с видеомагнитофоном. Нужна ли вам возможность программировать жалюзи, подобно видеомагнитофону, чтобы они сами открылись в 7:30 утра, изменяли угол наклона планок в 16:45-17:05, чтобы вечернее солнце не светило вам в глаза и, наконец, закрывались жалюзи в 19:45? Наверное, нет. Как определить нужное время? Оно меняется в зависимости от времени года и погоды. В пасмурный день вы захотите полностью открыть жалюзи, чтобы в комнате было как можно светлее.
Лучшее решение — использовать фотоэлемент. По умолчанию жалюзи будут открываться, когда освещенность превысит какое-то значение (то есть днем), и закрываться, когда она будет ниже заданного значения (вечером и ночью). Фотоэлемент также подаст команду изменить угол наклона планок, чтобы затенить комнату, когда на жалюзи падает слишком яркий прямой солнечный свет. Нужные параметры можно будет задавать при помощи круглого циферблата, установленного на пульте (при помощи того же циферблата вы можете вообще отключить пульт управления, когда уезжаете в отпуск). Таким образом, на пульте будет круглый циферблат, чтобы задавать программы, и два кулисных переключателя для ручного управления жалюзи.

Большинство людей сразу же понимает, что ответ должен быть 24 плюс-минус. Все проблема как раз в том, чтобы вычислить этот плюс-минус.

Сначала обратите внимание, что перекрытие стрелок — это абсолютно предсказуемое явление. Обе стрелки движутся с постоянной скоростью, следовательно, интервал времени между двумя последовательными перекрытиями постоянный.

Этот постоянный интервал чуть более часа. В полночь часовая и минутная стрелки точно совпадают. Минутной стрелке требуется ровно шестьдесят минут, чтобы описать полный круг, за то же самое время часовая стрелка проходит 1/12 часть круга и находится на отметке 1 час. Чтобы добраться до отметки 1 час, минутной стрелке потребуется пять минут, но за это время часовая стрелка еще немного продвинется вперед…

Перед тем как увлечься обсуждением парадокса Зенона, давайте пока предположим, что между последовательными перекрытиями стрелок проходит чуть больше, чем 65 минут. Мы также знаем, что если умножить этот точный интервал на неизвестное целое число, должно получиться ровно двадцать четыре числа, так как каждые двадцать четыре часа часовая и минутная стрелки точно перекрываются на отметке 12. На самом деле это происходит каждые двенадцать часов — ведь путь, который стрелки проходят с полуночи до полудня, точно совпадает с путем, который они проходят с полудня до полуночи.

Давайте подробно проанализируем, что происходит за двенадцать часов с полуночи до полудня. За этот период стрелки не могут совпасть двенадцать раз — в этом случае интервал между совпадениями стрелок был бы 12/12 — или ровно один час, а мы знаем, что на самом деле он чуть больше, чем 65 минут. Следовательно, за этот период стрелки могут совпасть лишь 11 раз. Это значит, что продолжительность интервала между перекрытиями стрелок 12/11, или 65,45 минуты. Это и должен быть точный интервал, который мы не смогли вычислить чуть ранее. Умножив одиннадцать на два, мы получаем двадцать два перекрытия стрелок за двадцать четыре часа. Таким образом, двадцать два — это точный ответ, если только вы не захотите учитывать и совпадение стрелок в начале суток в полночь и в конце суток в следующую полночь — в этом случае ответом будет двадцать три.

100 вопросов — сервис для тех, кто любит общение и новые знакомства. Узнай что-нибудь новое про своих старых знакомых или заведи новых. Задавай вопросы и отвечай на вопросы других — это модно и весело! Присоединяйся! Море вопросов и интересных собеседников! Всего пара кликов и ты с нами! 25 баллов в подарок!

Сколько раз за сутки встречаются часовая и минутная стрелки…

В сутках 24 часа. Каждый раз, когда минутная стрелка обгоняет часовую, они совпадают. И это происходит 1 раз в каждый час. с 12 до часу стрелки совпадают только 1 раз! Когда день начинается, стрелки совпадают- минутная стрелка догонит часовую не в первом часу, а только в начале второго. Такая ситуация повторится и в полдень, стрелки совпадут только после 13. Таким образом, минутная и часовая стрелки совпадут только 22 раза! Ответ:22

Ответы — Задачи о часах — Занимательные задачи и опыты…

Сколько раз в сутки часовая и минутная стрелки образуют прямой угол? Это довольно популярная головоломка. При кажущейся легкости и очевидности ответа, тем не менее, многие дают неверный ответ. Почему-то, многие полагают, что правильный ответ — это либо 24 (по количеству часов в сутках), либо 24*2=48.

Решение Сколько раз в сутки минутная стрелка на механических…

Оцени ответ Не нашёл ответ? Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Математика. Из 1 кг муколотуры можно сделать 25 школьных тетрадок сколько тетрадей можно сделать из 1 ц муколутуры? из 1 т макулотуры?

Сколько раз в сутки минутная стрелка обгоняет часовую?

Вам надоело постоянно опаздывать на важные встречи. Это легко исправить с помощью одной небольшой детали. Приобретите себе сколько раз в день стрелки часов совпадают и все ваши проблемы останутся позади. Это не только практичный аксессуар, но и стильное украшение на все случаи жизни. Они подойдут как женщинам, так и мужчинам, главное, выбрать для себя модель, которая подчеркнет вашу индивидуальность.

Задача про аналоговые часы с секундной стрелкой

Сколько раз на сутки встречаются все стрелки в часах?

В сутках 24 часа. Каждый раз,когда минутная стрелка обгоняет часовую, они совпадают. И это происходит 1 раз в каждый час.Но есть исключение:с 12 до часу стрелки совпадают только 1 раз! Когда день начинается, стрелки совпадают- минутная стрелка догонит часовую не в первом часу, а только в начале второго. Такая ситуация повторится и в полдень, стрелки совпадут только после 13. Таким образом, минутная и часовая стрелки совпадут только 22 раза!Ответ:В22

Сколько раз в день совпадают стрелки часов?

Постарайтесь как можно конкретнее описать причину нарушения, так вы поможете нам разобраться во всем гораздо быстрее Взяла механические часы и покрутила. Получилось 22 раза. В 00:00, 1:06, 2:12, 3:17, 4:23, 5:28, 6:33, 7:39, 8:44, 9:49, 10:55 — это одиннадцать, и еще 11 на втором обороте.

Сколько раз в день совпадают стрелки часов — Сколько раз…

За час минутная стрелка совершает 1 оборот, а часовая 1/12 оборота в ту же сторону. Скорость минутной стрелки относительно часовой 11/12 оборота в час. Если отсчёт начать в 12 часов, когда стрелки совпадают, то в следующий раз они встретятся через каждые 12/11 часа Итого за сутки (с 12 ч до 12 ч следующего дня) 23 раза. 23*31=713

Algebra-precalculus — Сколько раз стрелки часов совпадают…

Сколько раз в день стрелки часов совпадают?… — Мой вопрос.ru

Приведём один из вариантов возможных рассуждений. Любой инженер знает, что 210 = 1024. Будем считать, что это приблизительно 1000. Умножим 210 на себя шесть раз и получим 260. Это около 1000 в шестой степени или 1018, также известное как квинтиллион. Осталось только умножить его на 24 (16), чтобы получить искомое 264. Таким образом, очень приблизительный, но быстрый ответ будет 16 квинтиллионов.

2 Один день — 24 часа. Как только минутная стрелка обходит часовую, они пересекаются. Но есть и исключение, с 12 до 13 они совпадают всего один раз. Поэтому за день, часовая и минутная стрелки совпадут 22 раза. А вот на часах, где имеются три стрелки — секундная, минутная, часовая, совпадение лишь один раз — в двенадцать часов.

В какое время стрелки часов совпадают. Сколько раз в течение суток перекрываются часовая и минутная стрелки

info-4all.ru

Сколько Раз В Сутки Три Стрелки Часов Совпадают?

Ответы на поставленный вопрос носят в основном декларативный характер, но не как решение математической задачи. Правильный ответ, возможно, многим покажется неожиданным. Попробуем разобраться в проблеме, не прибегая к сложным приемам. Ясно, что стрелки в определенные периоды времени совпадают. Минутная обгоняет часовую, а секундная, в свою очередь, две ранее названные стрелки. Но речь ведется об одновременном совпадении трех стрелок. Следовательно, достаточно вычислить моменты совмещения минутной и часовой стрелок и определить, где будет находиться в это время секундная стрелка. Циферблат разделен на 12 часов и 60 делений (минут, секунд), которые и будем использовать в качестве определения местоположений стрелок. Теоретически примем три стрелки часов совпадающими в начале отчета времени, т. е. 12.00. Тогда в течении 12 часов совпадение часовой и минутной стрелок наступит 11 раз. Следовательно, можно вычислить и время их совмещений Тч=n*(1+1/11) в часах на циферблате, где n порядковый номер моментов совместного положения стрелок. Вычислим время первого n=1 совмещения в часах: Тч=1*(1+1/11)=1,0909…ч; в часах и минутах: Тм= 1ч+0,(09)*60 м=1ч+5,(45)м; в часах, минутах и секундах: Тс=1ч+5 м 0,(45)*60с=1ч+5м+27,(27) с. Как видим, секундная стрелка в нужный момент времени находится совсем в другом месте. Аналогичный результат и во всех других моментах времени, за исключением последнего, когда все стрелки приходят в исходное положение. Получается, теоретически можно вести речь о двух совпадениях в сутки. Практически установка стрелок на заводах или часовым мастером производится с некоторой погрешностью, пусть и малой. По этой причине три стрелки часов никогда не совпадают.

otvet.expert

Сколько раз в день стрелки часов совпадают?

Сколько раз в день стрелки часов совпадают?

Сколько раз за сутки встречаются часовая и минутная стрелки…

Ответы — Задачи о часах — Занимательные задачи и опыты…

Решение Сколько раз в сутки минутная стрелка на механических…

Сколько раз в сутки минутная стрелка обгоняет часовую?

Задача про аналоговые часы с секундной стрелкой

Сколько раз на сутки встречаются все стрелки в часах?

Сколько раз в день совпадают стрелки часов?

Сколько раз в день совпадают стрелки часов — Сколько раз…

Algebra-precalculus — Сколько раз стрелки часов совпадают…

Сколько раз в день стрелки часов совпадают?… — Мой вопрос.ru

Сколько раз в течение дня стрелки часов перекрываются?

Представьте себе аналоговые часы, установленные на 12 часов. Обратите внимание, что часовая и минутная стрелки перекрываются. Сколько раз в день часовая и минутная стрелки перекрываются? Как бы вы определили точное время дня, когда это происходит?

К тому времени, когда минутная стрелка прошла весь путь до 24 часов и вернулась на 12, через час (то есть в 1 час), часовая стрелка переместилась на 1.Через пять минут минутная стрелка достигает 1, но они не совсем сходятся там, потому что часовая стрелка переместилась бы на 1/12 расстояния между 1 и 2, чтобы показать 5 минут после 1. Итак, в следующий раз после 12 это минутная стрелка находится прямо над часовой стрелкой чуть позже 1:05 (точное время мы вычислим чуть позже).

Точно так же в следующий раз это произойдет немного позже 2:10. Потом чуть позже 3:15 и так далее.

Обратите внимание, что каждый раз, когда они встречаются, количество минут после часа продолжает увеличиваться, поэтому часовая стрелка переместилась бы ближе к следующему числу.После 11 часов минутная стрелка должна пройти весь путь, и к тому времени, когда они встретятся, она должна снова оказаться на 12 часах, поскольку мы знаем, как выглядят часы в это время. Таким образом, две руки перекрываются 11 раз за 12-часовой период. Таким образом, за 24 часа они перекрываются 22 раза.

Чтобы ответить на вторую часть вопроса, давайте попробуем вычислить немного дополнительного времени, необходимое минутной стрелке, чтобы догнать часовую стрелку через каждые 1:05 часа. Что ж, после 12 часов есть одиннадцать случаев, когда две стрелки совпадают, и поскольку стрелки часов движутся с постоянной скоростью, эти 11 событий равномерно распределены по циферблату, так что они находятся на расстоянии 1/11 часа. .Это 5,454545 минут. Другими словами, они встречаются каждые 1 час 5,454545 минут.

Точное время, когда они перекрываются (в часах), будет 1 + 1/11, 2 + 2/11, 3+ 3/11, вплоть до 11 + 11/11, то есть снова 12 часов.

Вопросы, связанные с этим:

В. Аналоговые часы показывают 2 часа прямо сейчас. В какое время часовая и минутная стрелки будут перекрывать друг друга в следующий раз?

В. Каков угол между часовой и минутной стрелками на отметке 4:10?

Выровненные стрелки часов

Небольшая небольшая головоломка на этой неделе, основанная на вопросе интервью, который я прочитал в Интернете.

Исходный вопрос был таким:

В какое время дня часовая и минутная стрелки аналоговых часов идеально совмещены?

На первый взгляд это может показаться тривиальным вопросом, затем вы понимаете, что часовая стрелка плавно и непрерывно движется по циферблату (хотя и медленнее, чем минутная стрелка) и не фиксируется на каждой квантованной часовой позиции в каждом часе. . Это немного усложняет, но не слишком.(Ответы: , а не 1:05, 2:10, 3:15…)

Совершенно ясно, что обе стрелки совпадают, когда ровно полночь (и полдень). Когда в следующий раз?

Это не 1:05, а немного больше, потому что к тому времени, когда минутная стрелка также окажется в положении «1 час», часовая стрелка немного продвинется вперед.

Минутная стрелка вращается вокруг циферблата в двенадцать раз быстрее, чем часовая стрелка (она совершает один оборот за час, в то время как часовая стрелка перемещается на один час, что составляет 1/12 часть циферблата).

В часах T минутная стрелка совершает T оборотов. За то же время часовая стрелка совершает долю Т / 12 оборотов. Используя градусы, мы можем видеть, что минутная стрелка движется со скоростью 360 ° в час, а часовая стрелка (360 ° / 12) = 30 ° в час.

Ниже приведен график, показывающий угол (в градусах) для обеих рук для значений T от 0 до 12. Там, где линии пересекаются (пример показан красным кружком), стрелки будут совпадать.

Это происходит в 11 разных местах между полуночью и (незадолго до этого) полуднем, а затем повторяется еще 11 раз во второй половине дня.

Мы можем вычислить точное время, посмотрев, когда угол между двумя руками равен нулю.

Определим углы H _T, M _T как углы (в градусах) стрелок (от положения «12 часов») после времени T (в часах).

H _T = 30T

M _T = 360T

Для того, чтобы стрелки были выровнены, разница между часовой и минутной стрелками должна быть равна нулю (после произвольного числа оборотов), где n — произвольное (целое) число оборотов.

M _T — H _T = 360 × n

360T — 30T = 330T = 360n

11T = 12n

Время можно найти, введя n = 0,1,2…

Т = 12н / 11

Стрелки перекрывают друг друга каждые (12/11) часов. Вот 22 результата (округлено до секунды):

00:00:00	12:00:00
1:05:27	1:05:27
2:10:55	2:10 : 55
3:16:22	15:16:22
4:21:49	16:21:49
5:27:16	17:27:16
6:32:44	6:32:44 PM
7:38:11 AM	19:38:11
8:43 : 38 AM	20:43:38
9:49:05	9:49:05
10:54:33 AM	22:54:33

Однако вопрос, который я хочу задать, является следующим логическим развитием этой проблемы.Что, если мы добавим секундную стрелку?

Часовая стрелка, Минутная стрелка, Секундная стрелка…

Изображение: Mark Turnauckas

В какое время дня часовая, минутная и секундная стрелки совпадают?

Как и раньше, давайте определим углы H _T, M _T, S _T как углы (в градусах) стрелок (от положения на 12 часов) после времени T (в часах). ).

H _T = 30T

M _T = 360T

S _T = 360T × 60 = 21600T

Для того, чтобы стрелки были выровнены, разница между парами углов должна быть равна нулю (после произвольного числа поворотов).

M _T — H _T = 360 × n

S _T — H _T = 360 × м

(где n и m — целые коэффициенты). Комбинируя уравнения, получаем:

360T — 30T = 330T = 360n

21600 зуб. — 30 зуб. = 21570 зуб. = 360 м

Эти упрощают:

11T = 12n

719T = 12 м

Даем результат:

719n = 11м

И 11, и 719 являются простыми числами и не имеют общих множителей.Итак (кроме тривиального случая n = m = 0), поскольку n должно быть кратным 11, скажем, n = 11x, для некоторого целого числа x. Тогда m = 719x, а T = 12x. Это показывает, что это происходит только после целого числа, кратного 12 часам, то есть в 12 часов.

Все места совмещения часовой и минутной стрелок (разница углов кратна 360 °) отличаются от всех мест совмещения часовой и секундной стрелок (кроме 12:00).

Это означает, что кроме полуночи (и полудня) есть нет других случаев, когда все три стрелки имеют точно такой же угол.

(Этот ответ имеет смысл, если подумать, потому что, если бы все трое выстроились в очередь, это должно было произойти и при двух составах, так что это должно было бы произойти в одном из 11 вычисленных ранее раз с помощью всего лишь часовая и минутная стрелки, и ни одна из них не соответствует положению секундной стрелки).

Насколько близко мы можем их получить?

Быстрый поиск в Интернете показывает, что Доктор Роб из The Math Forum также рассмотрел эту проблему и обнаружил, что самое близкое, что он мог найти для всех трех рук, — это время 5:27:27.3, когда все стрелки находятся в секторе 1,0014 градусов. Он продолжает напоминать нам, что это, вероятно, все еще видно невооруженным глазом, поскольку стрелки часов тонкие, а угол между секундными отметками составляет 6 °

Вы можете найти полный список всех статей здесь. Щелкните здесь, чтобы получать уведомления по электронной почте о новых статьях.

Сколько раз часовая и минутная стрелки составляют прямую линию?

Ни для кого не секрет, что минутная и часовая стрелки движутся с разной скоростью, однако есть определенные точки в их вращении, когда стрелки находятся в точных противоположных точках друг от друга, образуя прямую линию.

Точно, сколько раз это происходит, может появиться вопрос в математической викторине или даже как начало необычной беседы на вечеринке.

Независимо от того, где возникает вопрос, будьте уверены, что после прочтения этой статьи вы не только узнаете ответ, но и найдете его решение.

Краткий ответ на вопрос, сколько раз часовая и минутная стрелки составляют прямую линию за день: 22.

При 12-часовом отрезке стрелки часов 11 раз оказываются в точной противоположности друг другу, и, поскольку день составляет 24 часа, вы можете видеть стрелки в одном из этих 11 положений дважды в день, что дает нам 22 раза, что обе стрелки часов образуют прямую линию.

Точное время, когда руки находятся в этих положениях, следующее:

1. 12:33
2. 1:38
3. 2:44
4. 3:49
5. 4:54
6. 6:00
7. 7:06
8. 8:11
9 . 9:17
10. 10:23
11. 11:28

Если вы отследите время, начиная с 12:33, стрелки перейдут в это положение через час и пять минут, и вы сможете разделить только 12 часов на 11, одночасовое и пятиминутное деления.

Существует другой, более сложный способ получить этот ответ, который включает в себя ряд различных переменных, позволяющих определить, когда стрелки образуют угол 180 градусов.

Хотя сама формула может быть сложной, приятно видеть, как часы и циферблаты играют большую роль в преподавании и изучении математики.

Это может быть связано с тем, что циферблат представляет собой доступное и логичное визуальное представление времени, которое просто невозможно сопоставить.

Независимо от того, возникает ли этот вопрос в ходе логического теста или для начала разговора, вы можете быть уверены, что сможете легко ответить на него, даже включая время в день, когда стрелки образуют прямую линию.

Сколько раз перекрываются часовая и минутная стрелки за день

«давай, давай, давай !!!»

Эта проблема немного сложная. Я думал, что в начале было 25 раз. Причина заключалась в том, что они перекрывались в 0:00 (первый раз), затем начали работать, догоняли каждый час и, наконец, вернулись к 0:00. Таким образом, всего 1 + 24 = 25 раз.

Эй, я действительно не знаю, как об этом думать. Вы проигнорировали несколько условий:
1. Кто сказал, что он должен начинаться в 0:00?
2.Кто сказал, что часовая и минутная стрелки должны совпадать при запуске?
3. Неужели он нагоняет раз в час? Есть ли такая ситуация: в конце часа, когда случается наверстать упущенное, засчитывается ли это время как для этого, так и для другого часа?

Несколько онлайн-ответов:

1,22 раза
Время совпадения:
0:00 bai1: 06: ； 2 ： 12 ； 3: 17 ； 4: 22 ； 5: 27 ； 6: 33 ； 7: 38 ； 8: 43 ； 9: 49 ； 10 : 54 ； 12: 00 ； 13: 06: ； 14 ： 12 ； 15: 17 ； 16: 22 ； 17: 27 ； 18: 33 ； 19: 38 ； 20: 43 ； 21: 49 ； 22: 54。
Расчет метод:
Каждые 12 часов часовая стрелка поворачивается на один оборот, а минутная стрелка поворачивается 12 раз, то есть минутная стрелка совпадает с часовой стрелкой 11 раз, поэтому 0:00 принимается в качестве отправной точки, а часы делится на 11 равных частей в первой половине дня.Да; время для каждой шкалы n: [60n / 11]. [] означает целое число. 0≤n≤10. Во второй половине дня это время записывается как время после полудня, и время записывается по 24-часовому методу плюс 12 часов.
Минутная стрелка — это стрелка, которая движется на часах в минутах; игольчатые детали на поверхности таймеров, таких как часы и часы, отличаются от длинных и коротких стрелок. Короткая стрелка указывает на «час», которая называется «Часовая стрелка».

3.Часовая и минутная стрелки пересекаются 22 раза в день.
Анализ с 0: 00 ~ 24: 00.
Движение часовой стрелки и минутной стрелки чжи рассматривается как движение двух человек AB, участвующих в гонке на круговой дорожке Дао.
В течение 24 часов: AB начал работать с той же стартовой линии. В течение 24 часов A (представляющий часовую стрелку) пробежал 2 круга, а B (представляющий минутную стрелку) пробежал 24 круга.
Затем B пробежал еще 22 круга, что больше, чем A22 раза. Каждый раз более одного B встретятся с A, всего 22 раза.После того, как B пробежал 24 круга, A пробежал 2 круга и вернулся на ту же стартовую линию.

Сколько раз в день стрелки аналоговых часов перекрываются?

Здесь есть несколько загадок. Я собрал их в одну статью. Это все головоломки, о которых я раньше не слышал, так что все это было очень весело. Я также получил в Google несколько математических слов, которые я не использовал со времен универа.

Головоломка

  1) Сколько раз в день стрелки аналоговых часов перекрываются?
2) Если остановившиеся часы показывают правильные часы два раза в день, как часто правильные обратные часы? предполагая, что оба были в последний раз одинаковыми в 00:00?

Допущения

Мы не включаем вторичные руки.В наших часах есть только часовая и минутная стрелки.

Примечание. В Интернете могут быть более сформулированные решения этой проблемы. Вы можете использовать Google бесплатно.

Думаю, загадка 2) Начать проще.

  Если остановленные часы показывают правильные часы дважды в день, как часто правильные часы показывают обратные часы? предполагая, что оба были в последний раз одинаковыми в 00:00?

«Сколько раз часы показывают правильное время?» тот же вопрос, что и «Сколько раз часы показывают то же время, что и рабочие аналоговые часы?»

Для этих головоломок мы можем игнорировать минутную стрелку.Учитывая часовую стрелку, мы всегда можем определить положение минутной стрелки. Таким образом, если происходит столкновение часовых стрелок, мы знаем, что существует также столкновение минутных стрелок. (Существует функция, которая сопоставляет положение часовой стрелки с положением минутной стрелки. Эта функция предназначена (но не взаимно однозначно! Или биективно!)

Для двух часов мы будем считать рабочие аналоговые часы «контрольными» часами, которые идут на 1 час-расстояние / час . (Я визуализирую, как часовая стрелка перемещается из своего положения на циферблате на «12» и перемещается на расстояние до «1».Это расстояние между двумя числами на циферблате я называю часовым расстоянием. Прошу прощения за использование этой терминологии. )

Реверсивные часы будут работать на отметке -1 час / час . (Та же скорость, но отрицательная скорость).

Название часов	Время Сан-Димас (Контрольные часы)	Реверсивные часы
Время начала отсчета	00:00 (День 0)	00:00 (День 0)
Время через 1 час	01:00 (День 0)	23:00 (День -1)

Оба часа делают один полный оборот циферблата за 12 часов.

Когда оба часа в сумме преодолеют 12-часовой путь, они столкнутся.
Учитывая, что они движутся в противоположных направлениях от цифры «12» на циферблате, они начинают с 12-часовым расстоянием между ними.

Учитывая, что каждые часы покрывают 1 час-расстояние / час в противоположных направлениях, относительная скорость двух часов относительно друг друга составляет 2 часа-расстояние / час . (Часовые стрелки расходятся на это расстояние за час).А учитывая, что за один полный оборот циферблата приходится 12 часов, мы можем сказать, что эти два часа будут встречаться каждые 12-часовое расстояние / (2 часа / час) = 6 часов .

Итак, за 24 часа (1 день) два часа столкнутся 24 часа в день / 6 часов на столкновение = 4 столкновения .
Это время будет:

Время Сан-Димас (контрольные часы)	Часы с обратной скоростью
00:00 (День 0)	00:00 (День 0)
06:00 (День 0)	18:00 (День -1)
12:00 (День 0)	12:00 (День -1)
18:00 (День 0)	06:00 (День -1)

… а затем в полночь следующего дня.

Сколько раз в день часы, идущие с двукратной обратной скоростью, показывают точное время?

Думаю, этот вопрос также был размещен в Slack. Либо так, либо я начинаю придумывать себе лишние проблемы.

В этой ситуации, если оба отсчета запускаются в полночь, через один час контрольные часы покажут 1 час ночи, а часы с двойной обратной скоростью — 10 часов вечера.

Название часов	Время Сан-Димас (Контрольные часы)	Часы с 2-кратной обратной скоростью
Время начала отсчета	00:00 (День 0)	00:00 (День 0)
Время через 1 час	01:00 (День 0)	22:00 (день -1)

Сравнивая скорости двух часов, часовая стрелка контрольных часов движется со скоростью 1 час / час , а часы с двойной обратной скоростью движутся со скоростью -2 час-расстояние / час .Часы расходятся на 3 часа каждый час.

Следовательно, часы будут встречаться каждые 12-часовое расстояние / (3-часовое расстояние / час) = 4 часа .

Итак, в 24-часовом дне две часы будут сталкиваться 24 часа в сутки / 4 часа на столкновение = 6 столкновений .
Это время будет:

Время Сан-Димас (контрольные часы)	Часы с 2-кратной обратной скоростью
00:00 (День 0)	00:00 (День 0)
04:00 (День 0)	16:00 (День -1)
08:00 (День 0)	08:00 (день -1)
12:00 (День 0)	00:00 (День -1)
16:00 (День 0)	16:00 (день -2)
20:00 (День 0)	08:00 (день -2)

… а затем в полночь следующего дня.

Сколько раз в день часы, идущие с тройной скоростью, показывают точное время?

Сравниваем две часы:

Название часов	Время Сан-Димас (Контрольные часы)	Трехскоростные часы
Время начала отсчета	00:00 (День 0)	00:00 (День 0)
Время через 1 час	01:00 (День 0)	03:00 (День 0)

Часы с тройной скоростью покрывают +3 часа расстояния в час, однако контрольные часы отстают на расстояние 1 час каждый час.

Следовательно, общее отклонение между двумя часами составляет +2 час-расстояние / час .

Для 12-часового отклонения до истечения (т.е. одного столкновения) нам нужно 12-часовое расстояние / (2 часа-расстояние / час) = 6 часов

Т.е. столкновение происходит каждые 6 часов.

Итак, в 24-часовом дне два часа будут сталкиваться 24 часа в сутки / 6 часов на столкновение = 4 столкновения

Это время будет по адресу:

Время Сан-Димас (контрольные часы)	Трехскоростные часы
00:00 (День 0)	00:00 (День 0)
06:00 (День 0)	18:00 (День 0)
12:00 (День 0)	12:00 (День 1)
18:00 (День 0)	06:00 (2 день)

… а затем в полночь следующего дня.

Для часов, работающих со скоростью v (расстояние в часах / час) по сравнению с контрольными часами, эти часы будут отклоняться в часах на v - 1 каждый час. Таким образом, с учетом 12-часового циферблата:

Столкновение будет каждые 12 / | (v - 1) | часы

Да, если вы сравните два контрольных тактовых сигнала друг с другом, то вы делите на ноль. Я полагаю, вы могли бы сказать, что они бесконечно сталкиваются друг с другом.

Тогда количество столкновений за 24-часовой период будет:

24 / (12 / | (v - 1) |)

Это приводит к:

Будет | 2 (v - 1) | коллизий за 24 часа

Н.Б. Почему 1 - v или v - 1 ? С точки зрения контрольных часов, часы вдвое разгоняются на 1 час каждый час. Следовательно, v - 1 описывает отклонение в час. С точки зрения двукратных часов, это правильно, когда контрольные часы отстают на 1 час каждый час.

Например. Для 5-кратных реверсивных часов коллизия будет происходить каждые 12 / | ((- 5) - 1) | = 2 часа, что приводит к | 2 ((- 5) - 1) | = 12 столкновения за 24-часовой период.

Наконец, мы подошли к ответу на начальную загадку.

Мы можем смоделировать часовую стрелку как контрольные часы, а минутную — как часы с 12-кратной скоростью (за 1 час минутная стрелка преодолевает 12-часовое расстояние, совершая полный оборот циферблата).

Подставляя значения, мы получаем, что коллизия будет каждые 12 / | (12 - 1) | = 12/11 = ~ 1.0909 повторяющиеся часа.

Будет | 2 (12 - 1) | = 22 столкновения за 24-часовой период.

Формула способностей к часам, горячие клавиши и приемы решения проблем с часами | Предыдущие статьи

Clock Важные вопросы — страница 2
Clock Video Lecture — страница 3

Часы: Циферблат или циферблат часов представляет собой круг, окружность которого разделена на 60 равных частей, называемых минутными промежутками.У часов две стрелки, меньшая из которых называется часовой или короткой стрелкой, а большая — минутной или длинной.

Часы Важные формулы

За 60 минут минутная стрелка показывает 55 минут на часовой стрелке
Каждый час обе стрелки совпадают один раз.
Руки находятся на одной прямой линии, когда они совпадают или противоположны друг другу.
Когда две стрелки расположены под прямым углом, они находятся на расстоянии 15 минут друг от друга
Когда стрелки находятся в противоположных направлениях, они находятся на расстоянии 30 минут друг от друга
Угол, отслеживаемый часовой стрелкой за 12 часов = 360 °.
Угол отсчитывается минутной стрелкой за 60 мин. = 360 °.
Слишком быстро и слишком медленно: если часы показывают 8,15, когда правильное время, считается, что 8 на 15 минут быстрее.
С другой стороны, если он показывает 7,45, когда правильное время равно 8, считается, что это на 15 минут медленнее.

Решенные примеры проблемы часов

Вопрос — 1: Угол между минутной и часовой стрелкой часов, когда время 4: 20

Решение: Угол, измеренный часовой стрелкой в

Угол, прослеживаемый мин.сдача через 20 мин. =

Требуемый угол = (130 — 120) º = 10º.

Вопрос — 2: Сколько раз за день стрелки часов повернуты под прямым углом?
Решение: За 12 часов они 22 раза перпендикулярны.

За 24 часа они находятся под прямым углом 44 раза.

Вопрос -3: Сколько раз в день стрелки часов находятся на прямой линии, но противоположно по направлению?

Решение: Стрелки часов указывают в противоположных направлениях (по одной прямой) 11 раз за каждые 12 часов.(Потому что между 5 и 7 они указывают в противоположных направлениях только на 6 минут).

Итак, за день стрелки указывают в противоположных направлениях 22 раза

Вопрос — 4: В какое время между 9 и 10 часами стрелки часов будут вместе?
Решение: Чтобы быть вместе между 9 и 10 часами, минутная стрелка должна быть на 45 мин. пробелы. 55 мин. пробелы набраны за 60 мин.

45 мин. места приобретаются за мин.

Стрелки вместе на мин. 9

Важные вопросы из доклада за предыдущий год

0 из 20 завершенных вопросов

Вопросы:

Информация

Вы уже проходили викторину раньше.Следовательно, вы не можете запустить его снова.

Вы должны войти или зарегистрироваться, чтобы начать викторину.

Вы должны пройти следующую викторину, чтобы начать эту викторину:

0 из 20 вопросов ответил правильно

Ваше время:

Время истекло

Вы набрали 0 из 0 баллов, (0)

Средний балл
Ваша оценка

Вопрос 1 из 20
1 балл
На какой угол наклонены стрелки часов в положении 15 минут пятого?
Вопрос 2 из 20
1 балл
На какой линии в минутах между 3 и 4 часами обе стрелки будут совпадать? (Р.Р.Б.2002)
Правильно
В 3 часа минутная стрелка находится на 15-минутном интервале от часовой стрелки. Для совпадения она должна пройти 15-минутный интервал. 55 минут достигается за 60 минут.
15 мин. Набирается в
Стрелки совпадают при мин. Прошлом 3.
Неправильно
В 3 часа минутная стрелка отстоит от часовой стрелки на 15 минут. Для совпадения она должна пройти 15 минут. За 60 минут набирается 55 минут.
15 мин. Набирается в
Стрелки совпадают при мин.прошлое 3.
Вопрос 3 из 20
1 балл
В какое время между 9 и 10 часами стрелки часов будут вместе?
Вопрос 4 из 20
1 балл
В какое время между 7 и 8 часами стрелки часов будут на одной прямой, но не вместе? (Экзамен A.A.O., 2003)
Правильно
Когда стрелки часов находятся на одной прямой, но не вместе, они находятся на расстоянии 30 минут друг от друга.
В 7 часов они разнесены на 25 минут.
Минутная стрелка должна будет набрать всего 5 мин. пробелы.
Получено 55 мин. Места в
Требуемое время = мин. Прошлое 7
Неправильно
Когда стрелки часов находятся на одной прямой, но не вместе, они находятся на расстоянии 30 минут друг от друга.
В 7 часов они находятся на расстоянии 25 минут друг от друга.
Минутная стрелка должна будет набрать всего 5 мин. пробелы.
55 мин.площади приобретены в
Требуемое время = мин. Прошлое 7
Вопрос 5 из 20
1 балл
Часы, которые показывают равномерное ускорение: 2 минуты меньше в полдень понедельника и 4 минуты 48 секунд быстро в 14 часов. в понедельник. Когда это было правильно? (R.R.B.2001)
Вопрос 6 из 20
1 балл
Часы, которые отстают на 5 секунд за 3 минуты, были установлены прямо на 7 часов утра того же дня, когда часы показывали четверть второго часа, истинное время:
Вопрос 7 из 20
1 балл
Угол между минутной и часовой стрелками на часах, когда время равно 8.30, это
Вопрос 8 из 20
1 балл
Угол между минутной и часовой стрелками часов при времени 4,20 составляет:
Вопрос 9 из 20
1 балл
Точные часы показывают 6 часов утра. На какой градус повернется часовая стрелка, если часы показывают 4 часа дня?
Правильный
Угол, начерченный часовой стрелкой за 2 часа =
Неправильный
Угол, начерченный часовой стрелкой за 2 часа =
Вопрос 10 из 20
1 балл
Угол отражения между стрелками часов равен 10.25:
Правильный
Угол обведен часовой стрелкой на
Угол отсчитывается минутной стрелкой за 25 мин.
Неправильный
Угол, начерченный часовой стрелкой в 
Угол отсчитывается минутной стрелкой за 25 мин.
Вопрос 11 из 20
1 балл
Сколько раз за день стрелки часов поворачиваются под прямым углом? (I.A.S.1997)
Правильно
За 12 часов они расположены под прямым углом 22 раза по
За 24 часа они находятся под прямым углом 44 раза.
Неправильно
За 12 часов они под прямым углом 22 раза
За 24 часа они находятся под прямым углом 44 раза.
Вопрос 12 из 20
1 балл
Сколько раз в день стрелки часов находятся на прямой линии, но противоположно по направлению? (R.R.B.2003)
Правильно.
Стрелки часов указывают в противоположных направлениях (по одной прямой) 11 раз за каждые 12 часов (потому что между 5 и 7 они указывают в противоположных направлениях только на 6 часов).Таким образом, за день стрелки указывают в противоположных направлениях 22 раза.
Неправильно
Стрелки часов указывают в противоположных направлениях (по одной прямой) 11 раз за каждые 12 часов (потому что между 5 и 7 они указывают в противоположных направлениях только на 6 часов). руки указывают в противоположных направлениях 22 раза.
Вопрос 13 из 20
1 балл
Сколько теряют часы за день, если их стрелки совпадают каждые 64 минуты?
Правильный
55 мин.помещения покрываются за 60 мин.
60 мин. Пространства покрываются в
Убыток за 64 мин. =
Убыток за 24 часа =
Неправильно
55 мин. помещения покрываются за 60 мин.
60 мин. Пространства покрываются в
Убыток за 64 мин. =
Убыток за 24 часа =
Вопрос 14 из 20
1 балл
В какое время между 4 и 5 часами стрелки часов будут указывать в противоположных направлениях?
Правильный
В 4 часа стрелки часов 20 мин.пространств друг от друга.
Чтобы быть в противоположных направлениях, они должны находиться на расстоянии 30 минут друг от друга.
Минутная стрелка должна набрать 50 мин. Пробелов.
55 мин. Пробелов набираются за 60 мин.
Получено 50 мин. Места в
Требуемое время = мин. Прошлое 4
Неправильно
В 4 часа стрелки часов находятся на расстоянии 20 минут друг от друга.
Чтобы быть в противоположных направлениях, они должны находиться на расстоянии 30 минут друг от друга.
Минутная стрелка должна набрать 50 мин.пробелы.
55 мин. Пробелов набираются за 60 мин.
Получено 50 мин. Места в
Требуемое время = мин. Прошлое 4
Вопрос 15 из 20
1 балл
В какое время между 5.30 и 6 стрелки часов будут под прямым углом?
Правильный
В 5 часов стрелки 25 мин. пространств друг от друга.
ЧТОБЫ быть под прямым углом и между 5.30 и 6, минутная стрелка должна набрать (25 + 15) = 40 минутных интервалов.
55 мин.пробелы набираются за 60 мин.
Получено 40 мин. Места в
Требуемое время =
Неправильно
В 5 часов стрелки 25 мин. пространств друг от друга.
ЧТОБЫ быть под прямым углом и между 5.30 и 6, минутная стрелка должна набрать (25 + 15) = 40 минутных интервалов.
55 мин. пробелы набираются за 60 мин.
Получено 40 мин. Места в
Требуемое время =
Вопрос 16 из 20
1 балл
Часы запускаются в полдень.на 10 минут пятого часовая стрелка повернулась:
Правильный
Угол, отслеживаемый часовой стрелкой за 12 часов = 360
Угол, отслеживаемый часовой стрелкой за 5 часов 10 минут, т.е.
Неправильный
Угол, отслеживаемый часовой стрелкой за 12 часов = 360
Угол, отслеживаемый часовой стрелкой за 5 часов 10 минут, т.е.
Вопрос 17 из 20
1 балл
Точные часы показывают 8 часов утра. На сколько градусов будет вращаться часовая стрелка, когда часы показывают 2 часа дня? (I.A.S.2000)
Правильный
Угол, начерченный часовой стрелкой за 6 часов =
Неправильный
Угол, начерченный часовой стрелкой за 6 часов =
Вопрос 18 из 20
1 балл
В 3,40 часовая и минутная стрелки часов образуют угол:
Вопрос 19 из 20
1 балл
Сколько раз в день стрелки часов совпадают?
Правильный
Стрелки часов совпадают 11 раз за каждые 12 часов (Так как между 11 и 1 они совпадают только один, т.е.е. в 12:00).
Стрелки совпадают 22 раза в день.
Неправильно
Стрелки часов совпадают 11 раз за каждые 12 часов (поскольку между 11 и 1 они совпадают только один, то есть в 12 часов).
Стрелки совпадают 22 раза в день.
Вопрос 20 из 20
1 балл
Сколько раз в день стрелки часов прямые?
Правильно
За 12 часов стрелки совпадают или отклоняются в противоположном направлении 22 раза.
За 24 часа стрелки совпадают или поворачиваются в противоположную сторону 44 раза в день.
Неправильно
За 12 часов стрелки совпадают или поворачиваются в противоположном направлении 22 раза.
За 24 часа стрелки совпадают или поворачиваются в противоположную сторону 44 раза в день.

Важные видеоролики о проблеме часов

Clock Aptitude Вопросы и ответы

Q.1. Когда время 5:40, тогда каков угол между часовой и минутной стрелками?

А. 70 °

Б. 60 °

С. 74 °

Д. 80 °

Ответ и объяснение

Sol: Опция A
Используемая формула = θ = (11/2) M -30H, где H = часы, M = минуты
H = 5, M = 40
Требуемый угол, θ = (11/2) 40 -30 × 5 = 70 °

Q.2. В какое время между 2 и 3 часами стрелки часов будут вместе?

А.10 (10/11) мин. прошлое 2

Б. 10 мин. прошлое 2

C. 20 (10/11) мин. прошлое 2

Д. 12 мин. прошлое 2

Ответ и объяснение

Sol: Option A
В 2 часа часовая стрелка находится в положении 2, а минутная — в положении 12. Итак, они равны 10 минутам. пространств друг от друга. Чтобы быть вместе, минутная стрелка должна идти на 10 минут выше часовой стрелки.
Теперь, за 60 мин он выигрывает 55 минут. Таким образом, за (60/55) × 10 мин будет получено 10 минут.
= 10 (10/11) мин.
Стрелки совпадут на 10 (10/11) мин.прошлое 2.

Q.3. Что, когда время 6:32, тогда каков угол между часовой и минутной стрелками часов?

А. 2 °

Б. 4 °

С. 8 °

Д. 12 °

Ответ и объяснение

Sol: опция B
Используемая формула = θ = 30H — (11/2) M, где H = часы, M = минуты
H = 6, M = 32
Требуемый угол, θ = 30 × 6 — (11 / 2) 32 = 4 °

Q.4. Сколько раз в день совпадают стрелки часов?

Ответ и объяснение

Sol: Option C / strong>
Стрелки часов совпадают 11 раз за каждые 12 часов (поскольку между 11 и 1 они совпадают только один раз, т.е.е. в 12:00). Стрелки совпадают 22 раза в день.

В.5. В какое время между 1 и 2 часами стрелки часов повернутся под углом 180 °

A. 35 (5/11) мин. прошлое 1

Б. 40 мин. прошлое 1

C. 50 (4/11) мин. прошлое

Д. 38 (2/11) мин. прошлое 1

Ответ и объяснение

Sol: опция D
Предположим, что минутная стрелка будет на отметке 7, тогда стрелки образуют угол 180 °.он состоит из 7 равных частей. Каждая часть = 30 °
Общий угол = 7 × 30 ° = 210 °
Прирост на 11/2 ° за 1 минуту
Прирост на 210 ° за = (2/11) × 210 = 420/11 = 38 (2/11) мин. . прошлое 1

Обязательно прочтите статьи о проблемах с часами

Q.6. В какое время между 6 и 7 стрелки часов разнесены на 8 минут?

A. За 24 мин. 6

Б. 21 мин. После 6

C. 18 минут после 6

Д.20 мин за 6

Ответ и объяснение

Sol: Option A
Между x и (x + 1) часами две стрелки будут находиться на расстоянии t min в (5x ± t) (12/11) минут после x. Между 6 и 7 часами две стрелки будут составлять 8 минут. на расстоянии (5 6 –8) (12/11) = 264/11 = 24 мин после 6.

Q.7. Часы установлены на 13:00. Если он ускоряется на одну минуту в час, каково истинное время, когда часы показывают 6 часов вечера того же дня?

А.5 (7/61) мин за 5

Б. 55 (8/61) мин за 5

C. 55 (8/61) мин за 5

D. 56 (5/61) мин за 5

Ответ и объяснение

Sol: Опция B
Часы ускоряются на одну минуту в час. Через 61 минуту он показывает на 1 минуту меньше. Через 5 часов (300 минут) он покажет на 300/61 минуту меньше фактического времени будет 6 — (300/61) i.е. 55 (5/61) минут после 17:00.

Q8. Минутная стрелка часов обгоняет часовую стрелку с интервалом в 64 минуты точного времени. Сколько часы набирают или теряют за 12 часов?

A. 16 (5/11) мин.

B. 16 (4/11) мин.

C. 16 (6/11) мин.

D. 16 (7/11) мин.

Ответ и объяснение

Sol: Option B
60 минут получается за (60/55) × 60 = 65 (5/11) мин.Но они вместе через 64 мин.
Прирост за 65 минут = 65 (5/11) -64 = (16/11) м Прирост за 12 часов = (16/11) × (12 × 60/64) = 180/11 = 16 (4/11) ) мин.

Q9. Найдите время между 3 и 4, будут ли стрелки часов указывать в противоположном направлении?

A. 49 (1/11) мин за 3

B. 49 (3/11) мин за 3

C. 49 (2/11) мин за 3

D. 49 (4/11) мин за 3

Ответ и объяснение

Sol: Option A
Между x и (x + 1) часами две стрелки находятся в противоположных направлениях на (5x + 30) (12/11) мин после x.
Итак, между 3 и 4, 2 руки будут в противоположных направлениях на (5 3 + 30) (12/11)
= (45) (12/11) = 540/11 = 49 (1/11) мин. 3.

Q10. В какое время между 17 и 18 часами стрелки часов будут совпадать?

A. 21 (8/11) мин за 4

Б. 32 (8/11) мин за 5

C. 21 (5/11) мин после 4

D. 21 (4/11) мин за 4

Ответ и объяснение

Sol: Опция B
Между 17:00 и 18:00 стрелки часов будут вместе на отметке 5 6 (12/11) минут после 5 i.е. 360/11 = 32 (8/11) мин после 5.

Декабрь 2024
Пн	Вт	Ср	Чт	Пт	Сб	Вс
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

Сколько раз в сутки часовая и минутная стрелки совпадают: «Сколько раз в сутки пересекаются часовая и минутная стрелки часов?» – Яндекс.Кью

✅ Сколько раз за день пересекаются стрелки часов. Сколько раз в течение суток перекрываются часовая и минутная стрелки

У вас есть аналоговые часы с секундной стрелкой. Сколько раз в день все три стрелки часов накладываются друг на друга?

Сколько раз за сутки стрелки часов совпадают в одном положении

Сколько раз в день стрелки часов совпадают?

Сколько Раз В Сутки Три Стрелки Часов Совпадают?

Сколько раз в день стрелки часов совпадают?

Сколько раз за день пересекаются стрелки часов. Сколько раз в течение суток перекрываются часовая и минутная стрелки

Задача про аналоговые часы с секундной стрелкой

Задачи со стрелками исправных часов

Неделя математики.

Сколько раз за сутки стрелки часов совпадают в одном положении

Сколько раз в день стрелки часов совпадают?

Сколько Раз В Сутки Три Стрелки Часов Совпадают?

Сколько раз в день стрелки часов совпадают?

Сколько раз за день минутная стрелка. Сколько раз за сутки стрелки часов совпадают в одном положении

Сколько Раз В Сутки Три Стрелки Часов Совпадают?

Сколько раз в день стрелки часов совпадают?

Сколько раз за сутки встречаются часовая и минутная стрелки…

Ответы — Задачи о часах — Занимательные задачи и опыты…

Решение Сколько раз в сутки минутная стрелка на механических…

Сколько раз в сутки минутная стрелка обгоняет часовую?

Задача про аналоговые часы с секундной стрелкой

Сколько раз на сутки встречаются все стрелки в часах?

Сколько раз в день совпадают стрелки часов?

Сколько раз в день совпадают стрелки часов — Сколько раз…

Algebra-precalculus — Сколько раз стрелки часов совпадают…

Сколько раз в день стрелки часов совпадают?… — Мой вопрос.ru

В какое время стрелки часов совпадают. Сколько раз в течение суток перекрываются часовая и минутная стрелки

Сколько Раз В Сутки Три Стрелки Часов Совпадают?

Сколько раз в день стрелки часов совпадают?

Сколько раз за сутки встречаются часовая и минутная стрелки…

Ответы — Задачи о часах — Занимательные задачи и опыты…

Решение Сколько раз в сутки минутная стрелка на механических…

Сколько раз в сутки минутная стрелка обгоняет часовую?

Задача про аналоговые часы с секундной стрелкой

Сколько раз на сутки встречаются все стрелки в часах?

Сколько раз в день совпадают стрелки часов?

Сколько раз в день совпадают стрелки часов — Сколько раз…

Algebra-precalculus — Сколько раз стрелки часов совпадают…

Сколько раз в день стрелки часов совпадают?… — Мой вопрос.ru

Сколько раз в течение дня стрелки часов перекрываются?

Выровненные стрелки часов

Часовая стрелка, Минутная стрелка, Секундная стрелка…

Насколько близко мы можем их получить?

Сколько раз часовая и минутная стрелки составляют прямую линию?

Сколько раз перекрываются часовая и минутная стрелки за день

Сколько раз в день стрелки аналоговых часов перекрываются?

Головоломка

Допущения

Сколько раз в день часы, идущие с двукратной обратной скоростью, показывают точное время?

Сколько раз в день часы, идущие с тройной скоростью, показывают точное время?

Формула способностей к часам, горячие клавиши и приемы решения проблем с часами | Предыдущие статьи

Часы Важные формулы

Решенные примеры проблемы часов

Важные вопросы из доклада за предыдущий год

Информация

Важные видеоролики о проблеме часов

Clock Aptitude Вопросы и ответы

Добавить комментарий Отменить ответ