Дельта знак в математике: Дельта (буква) - это... Что такое Дельта (буква)?

Содержание

Что такое дельта 🚩 буква е в математике 🚩 Образование 🚩 Другое

Дельта — четвертая буква греческого алфавита, следующая после альфы, беты и гаммы. Она означает согласный звук «д». Аналоги этой буквы, обозначающие тот же звук, имеются практически во всех языках мира, за исключением, пожалуй, лишь иероглифических. Русская заглавная буква «Д» по начертанию очень похожа на заглавную греческую дельту, а в некоторых шрифтах сходный вид имеет и строчная буква «д».В математике заглавной дельтой обозначают разницу между двумя величинами, например, следующим образом:Δ(a;b)=c — это то же самое, что и a-b=cВ физике при помощи дельты обозначают шаг решетки, например, кристаллической или дифракционной. Помимо этого, данной буквой обозначают ряд других математических и физических величин. В одних случаях используют заглавную, в других случаях — строчную дельту (δ).Также заглавной дельтой обозначают соединение обмоток трехфазного двигателя треугольником (а буквой Y — соединение их звездой). Немало объектов, имеющих треугольную форму, называют дельтовидными. Существует дельтовидная мышца, кинескопы с дельтовидным расположением электронных прожекторов. Дельтой называют часть реки, а летательный аппарат с треугольным крылом носит название дельтаплана. Если при этом он оборудован двигателем, его называют мотодельтапланом.В качестве имени нарицательного термин «дельта» используется в отношении ряда географических объектов, одним из которых, кстати, является река. Название «Дельта-С» присвоено одному из отечественных домашних компьютеров, совместимых с Sinclair ZX Spectrum. Он давно не выпускается, зато теперь под названием «Дельта» производятся независимо друг от друга два вида других отечественных товаров: настольные лампы и комнатные логопериодические телевизионные антенны. Вторые имет форму, близкую к треугольной, за что они и получили свое название. А в США имя «Дельта» носят, также независимо друг от друга, авиакомпания и космическая ракета-носитель. Также именем этой греческой буквы назван производитель блоков питания, которые можно встретить практически в каждом современном мониторе.

Буквы греческого алфавита: названия, транскрипция на русском

Греческий алфавит создан примерно в IX—VIII вв. до н. э. С тех пор он непрерывно используется, а его буквы применяются в качестве символов/знаков в математике и других науках.

Ниже в табличном виде представлены прописные и строчные буквы греческого алфавита, их наименования и соответствие английскому языку, а также, названия и транскрипция на русском.


№	Заглавная буква	Строчная буква	)</nobr>» data-order=»Название<br><nobr>(англ.)</nobr>»>Название (англ.)	Название (рус.)	Английский эквивалент	Транскрипция (рус.)
1	Α	α	Alpha	альфа	a	[а]
2	Β	β	Beta	бета (вита)	b	[б], [в]
3	Γ	γ	Gamma	гамма	g	[г], [й]
4	Δ	δ	Delta	дельта	d	[д]
5	Ε	ε	Epsilon	эпсилон	e	[э]
6	Ζ	ζ	Zeta	дзета (зита)	z	[дз], [з]
7	Η	η	Eta	эта (ита)	h	[э], [и]
8	Θ	θ	Theta	тета (фита)	th	[т], [ф]
9	Ι	ι	Iota	йота	i	[и, й]
10	Κ	κ	Kappa	каппа	k	[к]
11	Λ	λ	Lambda	лямбда (лямда)	l	[л]
12	Μ	μ	Mu	мю (ми)	m	[м]
13	Ν	ν	Nu	ню (ни)	n	[н]
14	Ξ	ξ	Xi	кси	x	[кс]
15	Ο	ο	Omicron	омикрон	o	[о]
16	Π	π	Pi	пи	p	[п]
17	Ρ	ρ	Rho	ро	r	[р]
18	Σ	σ, ς *	Sigma	сигма	s	[с]
19	Τ	τ	Tau	тау (тав)	t	[т]
20	Υ	υ	Upsilon	ипсилон	u	[ю], [и]
21	Φ	φ	Phi	фи	ph	[ф]
22	Χ	χ	Chi	хи	ch	[х, хь]
23	Ψ	ψ	Psi	пси	ps	[пс]
24	Ω	ω	Omega	омега	o	[о]

microexcel. ru

* буква “σ” используется в начале и середине слова, “ς” – в конце.

Использование греческих букв для записи чисел

Буквы греческого алфавита, также, применялись для записи чисел. Для этого в стандартный алфавит, состоящий из 24 букв, были добавлены еще 4 (вышли из употребления) – дигамма (ϝ) или стигма (ϛ) для записи числа 6, коппа (ϟ) – для числа 90 и сампи (ϡ) – для значения 900.


Буква	Значение	Буква	Значение	Буква	Значение
α	1	ι	10	ρ	100
β	2	κ	20	σ	200
γ	3	λ	30	τ	300
δ	4	μ	40	υ	400
ε	5	ν	50	φ	500
ϝ или ϛ	6	ξ	60	χ	600
ζ	7	ο	70	ψ	700
η	8	π	80	ω	800
θ	9	ϟ	90	ϡ	900

miroexcel. ru

Греческая система счисления существует и в наши дни, однако, применяется редко, например, для нумерации глав книг.

2.Операции над множествами 1 курс

В теории множеств рассматривается семь основных
операций, это:

1.
Объединение множеств (A È B). Элемент,
принадлежащий полученному множеству, принадлежит
множеству А ИЛИ множеству В.

2.
Пересечение множеств (A Ç B). Элемент, принадлежащий полученному множеству, принадлежит
множеству А и множеству В.

3. Дополнение
множества А^/ (дополнение до множества обозначается штрихом справа)
состоит из всех элементов, принадлежащих универсальному множеству, и не
принадлежащих множеству А.

4. Относительное
дополнение, когда составляется дополнение не до универсального множества, а до
некоторого множества, скажем, Х. где относительное дополнение множество Х
Ç Ā, которое можно обозначить через Х — А «Х минус А».

5. Разность
множеств, обозначаемая знаком обратного слэджа, то есть \

6.
Симметрическая разность, обозначаемая знаком Δ ( который читается как дельта
или как треугольник)

7. Включение
одного множества в другое, обозначаемого знаком Ê .

Рассмотрим подробнее.

Объединение множеств,
A плюс B
записывается: A
È B, в
логике вместо плюс говорят A
или B

Знак равнозначности слева и справа «

Например, когда произведена операция сложения множеств, то
о каком — либо элементе, например x множества
A можно сказать:

x Î A
È B
«  x
Î A
или x
Î B
Графически, или по Венну, объединение

множеств рисуют так

Пересечение множеств
символически записывают так A
È B

Говорят, « A
крышка B » или « Пересечение
A и
B »

Графически,
заштрихованная часть является общей частью.

Множества считаются непересекающимися, если
у них нет общих элементов A
Ç B
= ø .
Изображать можно также, но внутри заштрихованной области ставят значок
«нуль». А если не пусто, можно записать так:

A
Ç B
¹ ø.

Дополнение множеств, когда для множества
М составляется множество М ^/ (дополнение для множества
обозначается штрихом справа) из всех тех и только тех элементов универсального
множества, (то есть полного множества), которые не содержатся во множестве М.

Существует абсолютное дополнение
множества (например, для множества А) до универсального множества
È
множеством Ā , элементы которого не входят в А.
Множество Ā является не чем иным как множеством элементов, {x
׀
xÏ A
}. В этом символическом выражении использован знак
׀ , называемый знаком делимости,
который означает, что элемент х относится к тем множествам, которые имеют
свойство делимости по признаку, Например, в множестве понятия «войны» включают
понятия войны справедливые и несправедливые

Существует относительное дополнение,
когда осуществляется дополнение не до универсального множества U
, а до множества, скажем, Х.

В этом случае, относительное дополнение Ā будет Х
Ç Ā, которое обозначается и
читается как «Х минус А» « Х – А», которое есть не что иное как
сокращение выражения { x Î X
׀
x Ï A}

Дельта математика знак — rohreighu.hackers-champloo.org

Дельта математика знак

Достаточно часто приходится в процессе набора различных документов вводить нам знак дельта. Именно его значение, а также способы ввода в различных приложениях под управлением такой. Математические знаки и Впервые встречается в трактате английского математика Джон Валиса В общую практику использования символ «дельта» вошёл после. В древнегреческом языке дельта произносилась как взрывной «д», в современном употребляемые в математике: Оператор. Математические знаки и символы используются сегодня практически в любой области знаний: Крайне распространенным знаком в математике является «дельта». Электростатика. Уравнение Пуассона является одним из важнейших уравнений электростатики. Дельта — это не только название греческой буквы. Дельтой обозначают разлиные величины в математике, физике.
Важно! Большинство звезд на небе являют собой целые системы. То, что мы видим как одну, реально может быть две, три, пять и даже сотни тел одной системы. От буквы «дельта» произошли латинская буква d и кириллическая . дельта-функции Дирака в математике; . буква — Знак (азбучный), письмена (множ. Уравне́ния Навье́ — Сто́кса — система дифференциальных уравнений в частных производных. $ \delta $ -функция — есть сингулярная обобщённая функция. Введена английским физиком Дираком. Математика — это ФЭНДОМ на портале Увлечения. ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ (1646-1716) Математика не была его единственной страстью.
Постоянно ищу как поставить знак треугольника с углом вверх который правильно называется — заглавная дельта и отображается как «Δ». Предполагаю, что размещаю. ИСТОРИЧЕСКИЙ СЛОВАРЬ. Агора – главная площадь Афин. Алеф – первая буква финикийского алфавита. Альфа, бета, гамма, дельта, эпсилон. / / Таблица математических символов. Знак «не принадлежит множеству» Множество натуральных.
Главная цель технологии развития критического мышления – развитие интеллектуальных. Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия, Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки. Информация — это, определение. Информация — это любые сведения, принимаемые и передаваемые, сохраняемые различными источниками. Α, α (название: альфа, греч. ἄλφα) — первая буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение. Дельта — это изменение на малую величину, например, В частности, в математике. 1) Обозначение треугольника 2) В высшей математике символ похожий на треугольник (дельта).
Первыми З. м. были знаки для изображения чисел — дельта (оператор О роли математических знаков великий русский математик Николай Лобачевский писал так:. Досить часто доводиться в процесі набору різних документів вводити нам знак дельта. Саме його значення, а також способи введення в різних додатках під. Кроме использования в правописании греков, символ начали активно применять в математике, геометрии, алгебре, физике, химии и географии. Записывается этот знак различными (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет Справочник по математике для средних. Знак вещественного понятие знака используется в других разделах математики, в том числе для нечисловых математических. Курси математики для школярів Дельта. Зняття відбуваються по вихідних днях у центрі «Маленьке щастя», що біля ЖК Софія, ЖК Щасливий, ЖК Софіївська Слободка. Купить товар Модные унисекс Для женщин Для мужчин Математика знак Дельта Сигма тета Нерегулярные Круглый Кольца anillos mujer 2018 новое поступление в категории Кольца.
FaqGuruPro.ru » Наука » Математика » Как рассчитать Записывается этот знак различными (приближенное значение х=8300). Абсолютная погрешность (или дельта икс) будет. перевернутый восклицательный знак греческая строчная буква дельта epsilon. Дельта-Плюс Строительные знак е ред русский язык 4 класс тренажер упражнения для занятий в школе и Математика 4 класс Упражнения для занятий в школе. Купить товар Модные Математика знак кольца для Унисекс Для женщин Для мужчин сплав Дельта Сигма тета Нерегулярные Круглый кольца подарок ювелирных изделий.
«дельта» обозначает разницу Если каким-то другим способом измеряется различие объектов и это различие может быть выражено числом, то (при Что означает буква delta. Изучим детально — как обозначается в математике площадь — какой буквой или знаком. Заодно уточним — как данный параметр вычисляется. Знак (математика) Это статья о понятии положительности и отрицательности. О математических символах см. таблицу математических. Знаки: плюс, минус, равно. В стране математики живут не только цифры и числа, но и разные математические знаки. Как можно понять язык «эпсилон-дельта»? а как Вы так быстро вставляете знаки и выражения из формул? Математика.

Links to Important Stuff

Знак дельта в excel

Информатик или даже простой обыватель может натолкнуться на простой значок греческого алфавита дельта Δ, которым обозначают множество значений. Данный знак является буквой алфавита греков и обозначает цифру четыре. Сформировалась дельта от буквы финикийского алфавита, которая означала направление, а конкретнее вход.

В наше время символ используется повсеместно в науках для:

Обозначения одноименной математической функции;
Обозначения частицы-дельта в физике;
Обозначения полноты в судостроительстве.

А также данный знак популярен в украшениях, татуировках и другой символике.

На нашем сайте вы можете найти полную кодировку данного символа.

Дельта — четвертая буква греческого алфавита. Символ верхнего регистра выглядит как треугольник — « Δ », а нижнего так « δ ». Рассмотрим способы печати знака в документе Ворд и в ячейках табличного редактора Excel.

В математике знак часто обозначает разницу между значениями температур или другими переменными. Например, начальное напряжение U1=220В, а конечное — U2=120В.
ΔU=U2–U1=220В-120В=100В

Вставка в Word

Рассмотрим 3 способа:

Напечатайте вместо знака английскую букву « D ».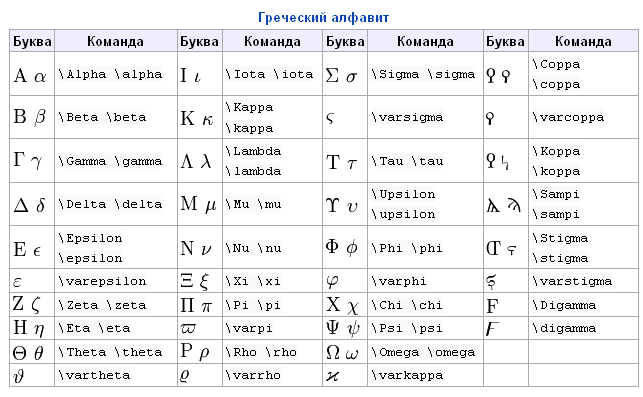 Выделите её и в верхнем меню на вкладке «Главная» установите шрифт «Symbol». Буква автоматически превратится в дельту.

В любом месте документа введите « 0394 » и нажмите горячие клавиши Alt и X . Цифры преобразуются в символ. Раскладка клавиатуры должна быть английской.

0 3 9 4 ➟ Alt + X = Δ

На полноценной клавиатуре с правым цифровым блоком клавиш можно воспользоваться следующим методом. Зажимаем Alt и набираем « 916 ». Вводить цифры надо именно на правом цифровом блоке.

Вставка в Excel

Предыдущие способы не походят в полной мере для применения в таблицах Excel. Например, конвертация буквы «D» в знак дельты может применяться только если в ячейке не будет других символов. Поэтому, самый лучший способ — воспользоваться вставкой.

В верхнем меню на вкладке «Вставка» выбираем пункт «Символ». В открывшемся окне указываем набор — «греческие и коптские символы». Здесь будет нужный знак.

Если нет возможности выбора набора, то внизу окна в поле «из:» установите значение «Юникод (шестн. )»

Знак дельта на Mac

Счастливые обладатели яблочной продукции Mac или Macbook могут использовать горячие клавиши Option + J .

Полезные советы или нет — ждём обратную связь в комментариях.

Зная десятичное значение кода символа, можно ввести этот символ с помощью комбинации клавиш ALT+код. Конечно, любой символ можно ввести через команду Вставка/ Текст/ Символ, но, иногда, например, при вводе пользовательского формата через Формат ячеек, эта команда недоступна.

Лучше пояснить ввод символов с помощью ALT кодов на примере. Введем символ ? (перечеркнутый 0) с помощью комбинации клавиш ALT+0216. Код 0216 – это десятичное представление кода системы UNICODE для символа ?. Символы и соответствующие коды можно посмотреть через инструмент Символ ( Вставка/ Текст/ Символ , т.е. на вкладке Вставка в группе Текст щелкните Символ).

Внимание! Для ввода цифр используйте цифровую клавиатуру (блок цифр справа!) и заранее перейти в раскладку Английский (США), CTRL+SHIFT или ALT+SHIFT (зависит от настроек компьютера).

Для ввода символа:

установите курсор в место, куда нужно вставить символ;
Удерживая ALT, наберите на цифровой клавиатуре 0216 и отпустите ALT. Символ должен отобразиться.

Использование клавиши ALT позволяет нам ввести любой символ из Таблицы символов без открытия самого диалогового окна, зная лишь его ALT код.

Заметим, что символ ? имеет шестнадцатеричный код 00В8, или соответствующий десятичный 0216. Часть символов имеет трехзначный ALT-код. Соответствующие коды смотрите, например, здесь ]]> http://www.theworldofstuff.com/characters/ ]]>

Будьте внимательны, не в каждом шрифте есть символ ? или тот, который нужен Вам. Попробуйте выбрать шрифт текста в ячейке, например, Wingdings3, и вы получите вместо ? стрелочку направленную вправо вниз.

вставляем нужный символ с помощью команды меню Вставка/ Текст/ Символ в ячейку;
копируем в Буфер обмена;
вставляем нестандартный символ в нужное место.

Символ перевернутый треугольник в ворде

При написании математических формул и уравнений в Ворде, пользователь часто прибегает к обычным символам, которые расположены на клавиатуре. Допустим, что нужно вставить знак дельта в Ворде, и обычная клавиатура уже не спасет. Решение проблемы существует, где находится знак и как его поставить, рассмотрим в статье.

Где найти дельту?

Раздел «Символ» известен своим огромным количеством разнообразных иероглифов и символов. В нашем случае, дельта тоже прячется здесь, как и многие другие знаки. А вот и вспомогательные шаги, которые приведут к знаку:

Метод 1: «Символ»

Откройте в ленте меню раздел «Вставка»;
В области «Символ» выберите кнопку с таким же названием «Символ»;
В окошечке со всеми недавно использованными знаками есть строчка «Другие символы» – жмём на неё;
В окне, что появится, нужно указать «Греческие и коптские символы» в пункте «Набор».
В списке найдите знак дельта, нажмите по нему, тем самым, выделив его
Нажмите на кнопку «Вставить».
Готово!

Метод 2: «Код знака»

Данный метод подойдет пользователю с феноменальной памятью. Можно поставить дельту с помощью кода знака.

Установите курсор на место, где должен стоять знак дельты и напишете 0394, затем нажмите «Alt +X», где Х это английская буква. Результат на лицо, все довольно легко.

В Word можно вставлять математические символы в уравнения и текст.

На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.

В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.

Щелкните стрелку рядом с названием набора символов и выберите набор символов, который вы хотите отобразить.

Щелкните нужный символ.

Доступные наборы символов

В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.

Основные математические символы

Часто используемые математические символы, такие как > и

Знаки, которых нет на клавиатуре.

Сегодняшний пост ответит на вопросы:

Как вставить в текст какой нибудь значок
Как поставить знак копирайта, торговой марки, стрелки и тд.
Как вставить в ник сердечко, крестик скобку и др.

То есть как вставить нестандартные знаки, которых нет на клавиатуре.

Для этого предназначены спец символы. Достаточно скопировать обозначение в код, и оно преобразуется в нужный вам знак. Ниже привожу таблицу специальных символов. Надеюсь пригодится и вам).

Таблица символов

Пользователей: 4048
Новичок: zkmzavod

Предыдущая ветка системы

Таблица Символов

HTML код	Dec код	Hex код	Вид символа	Описание
ASCII символы
Греческие буквы
HTML код	Dec код	Hex код	Вид символа	Описание
Стрелки
HTML код	Dec код	Hex код	Вид символа	Описание
Прочие символы
HTML код	Dec код	Hex код	Вид символа	Описание
Знаки пунктуации
HTML код	Dec код	Hex код	Вид символа	Описание
Общая пунктуация
HTML код	Dec код	Hex код	Вид символа	Описание
Знаки регистрации и авторских прав
HTML код	Dec код	Hex код	Вид символа	Описание
Знаки валют
HTML код	Dec код	Hex код	Вид символа	Описание

Что такое дельта в математике?

По мере развития математики на протяжении истории математикам требовалось все больше и больше символов для обозначения чисел, функций, множеств и уравнений, которые появлялись на свет. Поскольку большинство ученых в некоторой степени понимали греческий язык, буквы греческого алфавита были легким выбором для этих символов. В зависимости от области математики или естествознания греческая буква «дельта» может символизировать разные понятия.

Изменить

Дельта в верхнем регистре (Δ) часто означает «изменение» или «изменение» в математике.Например, если переменная «x» обозначает движение объекта, то «Δx» означает «изменение движения». Ученые часто используют это математическое значение дельты в физике, химии и технике, и оно часто встречается в словесных задачах.

Дискриминант

В алгебре дельта верхнего регистра (Δ) часто представляет собой дискриминант полиномиального уравнения, обычно квадратного уравнения. Для квадратичного ax² + bx + c, например, дискриминант этого уравнения будет равен b² — 4ac и будет выглядеть так: Δ = b² — 4ac.Дискриминант дает информацию о корнях квадратичной функции: в зависимости от значения Δ квадратичная функция может иметь два действительных корня, один действительный корень или два комплексных корня.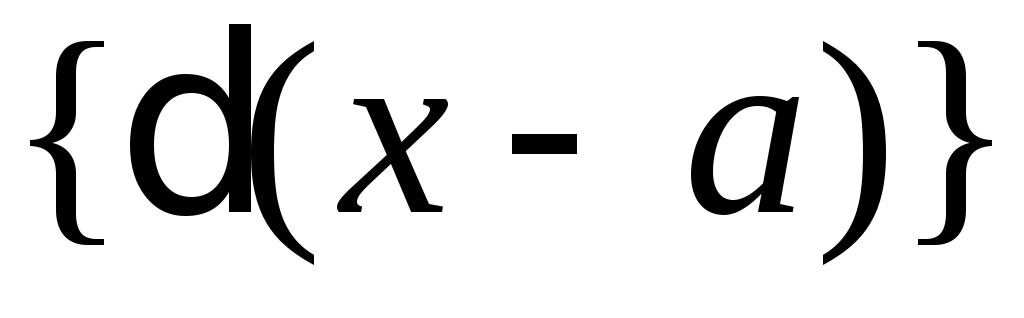

Углы

В геометрии дельта в нижнем регистре (δ) может представлять угол любой геометрической формы. Это потому, что геометрия уходит своими корнями в работы Евклида в Древней Греции, и математики затем отметили свои углы греческими буквами. Поскольку буквы просто представляют собой углы, знание греческого алфавита и его порядка не является необходимым для понимания их значения в данном контексте.

Частные производные

Производная функции — это мера бесконечно малых изменений одной из ее переменных, а латинская буква «d» представляет производную. Частные производные отличаются от обычных производных тем, что функция имеет несколько переменных, но учитывается только одна переменная: остальные переменные остаются неизменными. Дельта в нижнем регистре (δ) представляет частные производные, поэтому частная производная функции «f» выглядит так: δf по δx.

Дельта Кронекера

Дельта в нижнем регистре (δ) может также иметь более конкретную функцию в продвинутой математике. Дельта Кронекера, например, представляет собой взаимосвязь между двумя интегральными переменными, которая равна 1, если две переменные равны, и 0, если они не равны. Большинству студентов-математиков не придется беспокоиться об этих значениях дельты, пока их изучение не станет очень продвинутым.

Что такое Дельта? — Определение и концепция — Видео и стенограмма урока

Что означает дельта?

Дельта в верхнем регистре имеет два различных математических значения.Оба значения начинаются с буквы D, как и греческая буква, которая должна помочь вам их запомнить:

Разница — наиболее распространенное значение дельты верхнего регистра. Это просто разница или изменение в определенной величине. Когда мы говорим, например, дельта y , мы имеем в виду изменение y или насколько изменится y .
Дискриминант — второе по распространенности значение дельты верхнего регистра. Дискриминант находится в квадратной формуле и определяет количество решений, которые имеет конкретное квадратное уравнение.

Дельта в нижнем регистре чаще встречается в исчислении. Его значение также начинается с буквы D: расстояние от предела в исчислении. Он используется при расчете пределов в расчетах. Первые два значения являются наиболее распространенными, и с ними связаны формулы. Мы обсудим эти два здесь и покажем вам формулы. Третье значение строго то, значение и не имеет связанной формулы. Поскольку формулы, которую можно было бы показать, нет, мы не будем углубляться в это значение.

Дельта как разница

Дельта чаще всего означает различие или изменение чего-либо.Обычно вы слышите или видите это как дельта y , дельта t , дельта x и т. Д. Дельта возникает чаще всего, когда вы работаете со скоростью, ускорением или чем-либо, что меняется. Наклон линии, например, можно обозначить как дельту y по сравнению с дельтой x .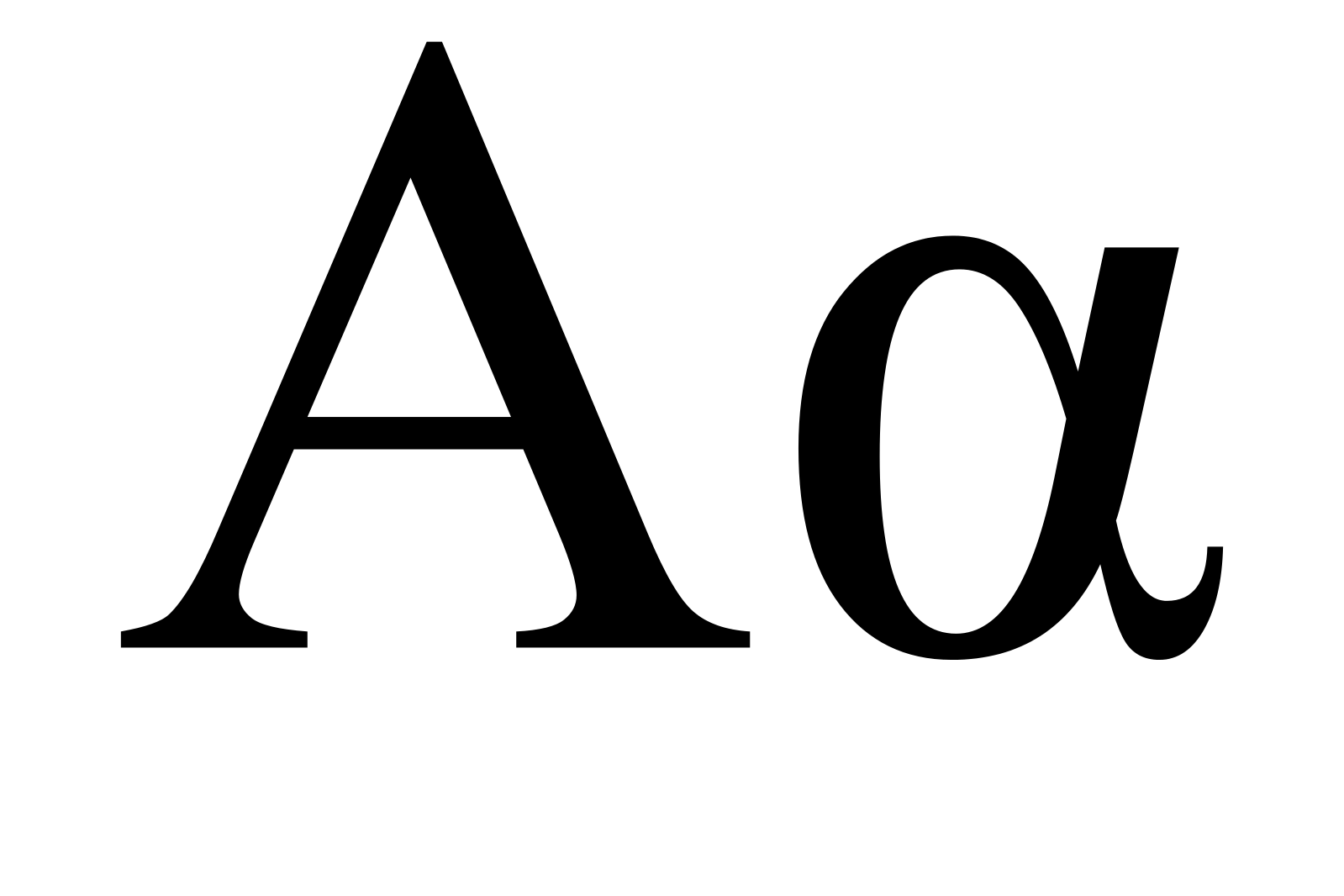 Из наклона мы можем получить формулу для дельты:

Чтобы использовать дельта-оператор в качестве разницы, у вас должны быть две точки для работы.Вам нужна начальная и конечная точки или две промежуточные точки, если вы ищете конкретную разницу. Чтобы вычислить изменение, вы вычитаете начальную точку из конечной точки. Так, например, если ваш y начинается с трех и заканчивается шестью, тогда ваша дельта y будет 6 — 3 = 3.

Дельта как дискриминант

Хотя вы можете увидеть формулу для дискриминанта сам по себе на самом деле имеет символ, который представляет собой дельту верхнего регистра:

При работе с дискриминантами вас могут попросить найти дискриминант или дельту в зависимости от того, кто спрашивает.Оба приемлемы и относятся к одному и тому же, когда вы работаете с квадратиками. Буквы a , b и c взяты из квадратичной функции при записи в стандартной форме:

Три буквы — это коэффициенты каждого соответствующего члена в квадратичной системе.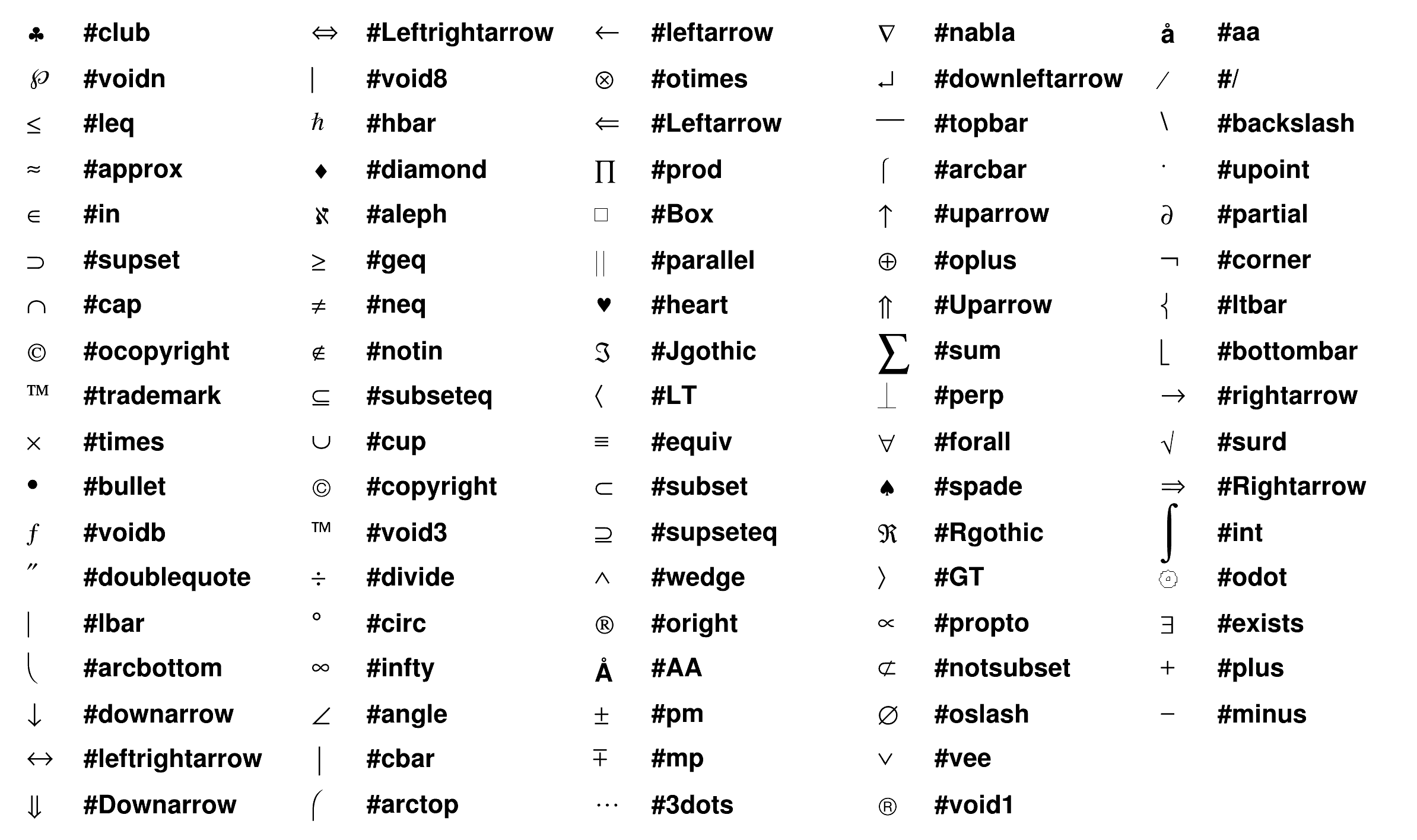 Чтобы вычислить дискриминант или дельту квадратичного, вы подставляете значения для ваших букв и вычисляете. Например, если a = 1, b = 2 и c = 2, то моя дельта будет 4-4 * 1 * 2 = 4-8 = -4.

Краткое содержание урока

Два наиболее распространенных варианта использования дельты связаны с заглавной версией греческой буквы. Два наиболее распространенных значения — это различие и дискриминант. Дельта в нижнем регистре используется в исчислении для обозначения расстояния от предела. Два значения дельты в верхнем регистре имеют формулы, которые вы можете использовать для их вычисления. Значение в нижнем регистре — это строго определение без соответствующей формулы.

Результаты обучения

Когда вы закончите, вы сможете:

Определить дельта-символ
Укажите значения дельты верхнего и нижнего регистра
Напишите уравнения для двух значений дельты верхнего регистра

% PDF-1. 4
%
6 0 obj>
эндобдж

xref
6 103
0000000016 00000 н.
0000002698 00000 н.
0000002774 00000 н.
0000002950 00000 н.
0000003223 00000 н.
0000003558 00000 н.
0000004285 00000 н.
0000004642 00000 п.
0000005517 00000 н.
0000005776 00000 н.
0000006459 00000 н.
0000006970 00000 н.
0000007141 00000 п.
0000008741 00000 н.
0000009131 00000 п.
0000009601 00000 п.
0000010345 00000 п.
0000010800 00000 п.
0000012374 00000 п.
0000013577 00000 п.
0000014809 00000 п.
0000014949 00000 п.
0000016189 00000 п.
0000016335 00000 п.
0000016768 00000 п.
0000016973 00000 п.
0000018645 00000 п.
0000018801 00000 п.
0000018961 00000 п.
0000019418 00000 п.
0000021160 00000 п.
0000022869 00000 п.
0000034220 00000 п.
0000034528 00000 п.
0000034847 00000 п.
0000035007 00000 п.
0000035317 00000 п.
0000035509 00000 п.
0000035562 00000 п.
0000036057 00000 п.
0000036278 00000 н.
0000036360 00000 п.
0000036772 00000 н.
0000036975 00000 п.
0000037275 00000 п.
0000037343 00000 п.
0000037991 00000 п.
0000038198 00000 п.
0000038502 00000 п.
0000038575 00000 п.
0000039172 00000 п.
0000039422 00000 п.
0000039534 00000 п.
0000039966 00000 н.
0000040154 00000 п.
0000040445 00000 п.
0000040498 00000 п.
0000040677 00000 п.
0000042354 00000 п.
0000042571 00000 п.
0000042928 00000 п.
0000043036 00000 п.
0000050174 00000 п.
0000050642 00000 п.
0000051076 00000 п.
0000051430 00000 п.
0000052259 00000 п.
0000052460 00000 п.
0000052781 00000 п.
0000052862 00000 п.
0000058335 00000 п.
0000058730 00000 п.
0000059147 00000 п.
0000059414 00000 п.
0000060709 00000 п.
0000060924 00000 п.
0000061277 00000 п.
0000061377 00000 п.
0000067861 00000 п.
0000068352 00000 п.
0000068762 00000 п.
0000069134 00000 п.
0000074302 00000 п.
0000074577 00000 п.
0000074895 00000 п.
0000075036 00000 п.
0000075478 00000 п.
0000075669 00000 п.
0000075969 00000 п.
0000076028 00000 п.
0000077338 00000 п.
0000077566 00000 п.
0000077904 00000 п.
0000078012 00000 п. V # ~ ۙ) @

Дельта-символов

Дельта-символ	Дельта-имя	Десятичное число	Шестнадцатеричное
ƍ	Латинская строчная буква с поворотом Дельта	& # 397;	& # x018D;
Δ	Дельта греческой заглавной буквы	& # 916;	& # x0394;
δ	Греческая строчная буква дельта	& # 948;	& # x03B4;
ᵟ	Буква модификатора Строчная дельта	& # 7519;	& # x1D5F;
ẟ	Строчная латинская буква дельта	& # 7839;	& # x1E9F;
≜	Дельта равна	& # 8796;	& # x225C;
⍋	Функциональный символ Apl Delta Stile	& # 9035;	& # x234B;
⍍	Функциональный символ Apl Quad Delta	& # 9037;	& # x234D;
⍙	Функциональный символ Apl Дельта Нижняя планка	& # 9049;	& # x2359;
𐎄	Угаритское письмо Дельта	& # 66436;	& # x10384;
𝚫	Математический жирный шрифт Дельта капитала	& # 120491;	& # x1D6AB;
𝛅	Математический полужирный, маленькая дельта	& # 120517;	& # x1D6C5;
𝛥	Математический курсив Дельта заглавной буквы	& # 120549;	& # x1D6E5;
𝛿	Математический курсив Малая дельта	& # 120575;	& # x1D6FF;
𝜟	Математический полужирный курсив Дельта заглавной буквы	& # 120607;	& # x1D71F;
𝜹	Математический полужирный курсив Малая дельта	& # 120633;	& # x1D739;
𝝙	Математический шрифт без засечек жирным шрифтом Дельта заглавной буквы	& # 120665;	& # x1D759;
𝝳	Математический шрифт без засечек жирный, малый дельта	& # 120691;	& # x1D773;
𝞓	Математический шрифт без засечек жирный курсив Заглавная дельта	& # 120723;	& # x1D793;
𝞭	Математический шрифт без засечек жирный курсив малый дельта	& # 120749;	& # x1D7AD;

Скопируйте и вставьте дельта-символ или используйте десятичное, шестнадцатеричное число или HTML-код Unicode на социальных сайтах, в своем блоге или в документе.

Дельта-символ Варианты предварительного просмотра

Дельта-символ	Цвет	Курсив
ƍ	Латинская строчная буква с поворотом Дельта-красный	ƍ
ƍ	Латинская строчная буква с поворотом Дельта-оранжевый
ƍ	Строчная латинская буква, повернутая дельта-розовая	ƍ
ƍ	Строчная латинская буква, повернутая дельта-зеленая	ƍ
ƍ	Латинская строчная буква повернутая дельта-королевский синий	ƍ
ƍ	Строчная латинская буква дельта-фиолетовый	ƍ
Δ	Дельта греческой заглавной буквы красный	Δ
Δ	Дельта греческой заглавной буквы оранжевый	Δ
Δ	Греческая заглавная буква Дельта розовый	Δ
Δ	Дельта греческой заглавной буквы зеленый	Δ
Δ	Дельта греческой заглавной буквы королевский синий	Δ
Δ	Дельта греческой заглавной буквы фиолетовый	Δ

Греческие буквы в математике — Семпер Fi Mathematics

Итак, вам, вероятно, интересно, что означают все эти греческие буквы в математике. Да, я знаю, они могут немного сбивать с толку. Однако, если вы планируете углубиться в математику, вы это увидите. Вот краткое руководство о том, что означает каждая греческая буква в математике.

Alpha: α

Это строчная альфа. Буква Alpha в нижнем регистре используется для двух вещей:

1. Ее можно использовать для обозначения угла. Часто, если мы хотим разделить два разных угла, мы обозначаем один как альфа, а другой как другую букву, что мы обсудим позже.

2. В статистике буква «альфа» в нижнем регистре может обозначать уровни значимости под кривой.

Альфа в верхнем регистре не используется в математике. Между прочим, он похож на обычную пятёрку. Вы ведь знаете, как выглядит буква А, верно?

Бета: β

Греческая буква Бета. Прописная буква Beta похожа на букву B, поэтому в математике она не используется. Нижний регистр Beta тоже выглядит как B, но более «изогнутый».

1. Бета в нижнем регистре может определять вторичный угол. Так же, как в нижнем регистре Alpha, если мы обозначим один угол как Alpha, мы можем обозначить другой угол как Beta.

2. Бета в нижнем регистре также может использоваться в статистике для регрессионного анализа.

Гамма: Γ γ

Первый — Гамма в верхнем регистре. Это похоже на перевернутую L. Нижний регистр Гамма выглядит как строчная y. Оба используются в математике, хотя здесь мы сосредоточимся только на прописной гамме, поскольку на этом веб-сайте мы не используем строчную гамму.

1.Гамма в верхнем регистре используется в исчислении по отношению к гамма-функции. Это может помочь нам определить факториал комплексного числа.

О, а смертоносные гамма-всплески? Это основано на греческой букве.

Дельта: Δ δ

Дельта имеет множество применений в математике. Прописная дельта выглядит как треугольник. Если он перевернут, он называется del. Строчная Дельта вроде как вишенка. Подумайте о строчной букве O со стержнем сверху.

1. Вы уже видели дельту в верхнем регистре на уроках алгебры 1.Дельта в верхнем регистре представляет собой изменение между двумя величинами. В формуле наклона используется дельта верхнего регистра.

2. Дельта в нижнем регистре может использоваться для определения предела или непрерывности функции в исчислении.

Эпсилон: Ε ε

Это Эпсилон. Верхний регистр Epsilon похож на букву E. Нижний регистр Epsilon также похож на верхний регистр E, но более изогнут. Эпсилон в верхнем регистре не используется в математике.

1. Эпсилон в нижнем регистре используется в реальном анализе, когда мы имеем дело с небольшим оператором.Мы увидим их, когда начнем доказывать пределы.

Дзета: Ζ ζ

Прописная Дзета выглядит как заглавная буква Z. Достаточно просто. Строчная Зета выглядит глупо. Это похоже на заглавную C, но с петлей сверху и кривой снизу. Ага, тупой. Однако строчная версия Зетов находит применение в математике.

1. Дзета в нижнем регистре используется для определения дзета-функции Римана в исчислении. Я мало что знаю об этом после этого.

Eta: Η η

Заглавная Eta, как ни странно, выглядит как заглавная H.Эта строчная Eta выглядит как удлиненная строчная буква n. Обратите внимание, что правая часть строчной Eta длиннее левой. Как и большинство заглавных греческих букв, которые мы рассмотрели, заглавная эта не используется в математике. Эта строчная буква имеет несколько применений.

1. Эта строчная буква Eta является линейным предсказателем обобщенной линейной модели. Между прочим, это статистика. Эта строчная буква Eta может использоваться для демонстрации эластичности в экономике.

Theta: Θ θ

Вы уже видели тету в нижнем регистре, но не в верхнем регистре.Они оба выглядят одинаково, но есть большая разница в размере буквы «О» в тете. Буква «О» в заглавной версии больше и шире.

1. Тета в верхнем регистре используется для обозначения температуры в системе СИ. Письмо должно быть выделено курсивом.

2. Тета в нижнем регистре обозначает определенный угол. Я часто использую строчные буквы Theta на своих уроках Precalculus, поэтому ищите их, когда у вас будет возможность.

Йота: Ι ι

Йота определить легко. Прописная йота выглядит как заглавная I.Строчная йота выглядит как строчная i, но без точки сверху. Йота в верхнем регистре не используется, но в нижнем регистре используется ограниченное количество раз. Когда я имею в виду ограниченный, я имею в виду ограниченный.

1. Йота в нижнем регистре используется для отображений включения в абстрактной алгебре.

Каппа: Κ κ

Каппу глупо легко распознать. Каппа в верхнем регистре выглядит как каппа в верхнем регистре K. Каппа в нижнем регистре — это уменьшенная версия буквы K в верхнем регистре. Думайте о каппе в нижнем регистре как о нижнем регистре k без удлиненной левой части. Прописные буквы Каппа не используются в математике, но, как ни странно, строчные буквы используются.

1. Каппа в нижнем регистре используется для обозначения кривизны кривой. Обычно это преподается в Исчислении III или любом другом курсе векторного исчисления, который будет рассмотрен позже.

Лямбда: Λ λ

Лямбда выглядит странно. Прописная лямбда выглядит как перевернутая заглавная буква V. Строчная лямбда выглядит как перевернутая строчная буква y.

1. Лямбда в верхнем регистре используется для определения диагональной матрицы собственных значений матрицы. Другими словами, если вы не специализируетесь на математике, вы не будете этим пользоваться.

2. Лямбда в нижнем регистре используется как множитель Лагранжа в исчислении. Он также используется для нахождения собственных значений матрицы в линейной алгебре.

Mu: Μ μ

Mu довольно легко идентифицировать. Верхний регистр Mu похож на верхний регистр M. Нижний регистр Mu выглядит как нижний регистр u, но с удлиненной левой стороной. Классный трюк для запоминания: прописные и строчные буквы Mu означают Mu. Круто, да?

1. Строчная Mu имеет два основных применения. Первый используется как среднее значение совокупности при нормальном распределении в статистике и вероятности.

2. В основном Mu используется в качестве префикса измерения. Он используется как префикс измерения микро. Обычно 1 мкм или один микрометр измеряется при 1 x 10 ^-6. Кстати, меньше миллиметра.

Nu: Ν ν

Nu довольно проста. Прописные буквы Nu — это заглавная N. В математике она не используется. Нижний регистр Nu — это нижний регистр v.

1. Нижний регистр Nu используется в статистике для обозначения степени свободы. Не знаю, что это значит? Тогда возьмите статистику.

Xi: Ξ ξ

Xi выглядит еще глупее, чем строчная Зета. На самом деле Си выглядит идиотским. Прописная буква Xi выглядит как заглавная E, но с отсутствующей левой стороной. Строчная Си выглядит как странная пышная заглавная E.

1. Заглавная Си не используется на этом веб-сайте, но имеет ограниченное применение в математике. Исследуйте его, если чувствуете себя лягушкой.

2. Буква Xi в нижнем регистре используется в статистике вероятности. Он просто представляет собой случайную величину.Вот и все, сэр или мэм.

Omicron: Ο ο

Как и Kappa, Omicron до глупости прост. На самом деле, это проще, чем Каппа. Если вы знаете разницу между заглавной и строчной буквой O, то вы знаете заглавную и строчную буквы Omicron.

Омикрон не используется в математике из-за его почти полного сходства с нулем.

Pi: Π π

Раньше вы видели строчные буквы Pi, но не прописные. Пи в верхнем регистре выглядит как Пи в нижнем регистре, но большего размера.Подумайте о двух столицах, соединенных вместе. Вы знаете, как выглядит строчная буква Пи.

1. Пи в верхнем регистре используется как оператор произведения в исчислении. Его также можно использовать для отображения вероятностного обозначения продукта.

2. Пи в нижнем регистре используется как иррациональное число 3,14 и некоторые изменения. Опять же, вы видели строчные буквы Пи еще в начальной школе.

Rho: Ρ ρ

Rho выглядит как заглавная и строчная P. Как и Omicron, если вы знаете прописную и строчную букву P, знать прописную и строчную Rho будет несложно.

1. Rho в верхнем регистре не используется на этом веб-сайте, поэтому не беспокойтесь.

2. Rho в нижнем регистре используется в трехмерном исчислении, а именно в сферической системе координат, которая представляет собой трехмерную визуализацию полярной системы координат. Rho в нижнем регистре представляет радиус в сферической системе, как и r в полярной системе. Использование очень похоже.

Сигма: Σ σ ς

Да, существует три различных формы сигмы. Заглавная сигма выглядит как заглавная E, но средняя диагональ больше, чем E.У строчной сигмы есть две разновидности: первая выглядит как строчная o, за исключением того, что у нее меньший стержень, чем у строчной дельты. Вторая форма сигмы называется окончательной формой и используется в конце слова, но только в том случае, если ни одна из используемых букв не является прописной. В математике используются только первые две формы сигмы.

1. Сигма в верхнем регистре используется в обозначении суммирования в алгебре II. Это также называется сигма-нотацией, которая находит сумму некоторого большого количества.

2. Строчная сигма в основном используется в статистике и представляет собой стандартное отклонение генеральной совокупности.Он также представляет сигма-функцию в теории чисел, когда мы смотрим на сумму делителей.

Тау: Τ τ

Как Каппа и Омикрон, Тау очень легко запомнить, поскольку они оба выглядят как прописные и строчные буквы T. Прописные буквы Тау не используются в математике.

1. Тау в нижнем регистре используется для обозначения кручения кривой. Он также используется в функции tau, которая сообщает нам количество делителей целого числа.

Ипсилон: Υ υ

Ипсилон странный.Верхний регистр Upsilon выглядит как заглавная Y. Нижний регистр Upsilon выглядит как курсивный нижний регистр v. Ни одна из версий Upsilon не используется в математике, но активно используется в других науках.

Phi: Φ φ

Phi — самый странный. Оба они похожи на буквы О, через которые проходит вертикальная черта. Пи прописными буквами выглядит так, как я только что описал. Строчная фи выглядит как вилы.

1. Прописные буквы Phi используются для отображения параметризации поверхности в векторном исчислении.Да, мы рассмотрим это на этом веб-сайте … в конце концов. Phi также используется для функции Эйлера в теории чисел, которая сообщает нам количество простых множителей в числе.

2. Фи в нижнем регистре иногда используется как дополнительный угол по отношению к Тета. Если альфа и бета не используются, то тета и фи будут использоваться вместе.

Chi: Χ χ

Chi — еще одна странность. Чи — это, по сути, заглавная буква X. Разница в том, что прописная ци выглядит как заглавная X. Строчная ци издалека выглядит как знак процента, но выглядит как прописная заглавная буква X.

1. Чи в нижнем регистре используется в статистике, где используется для проверки гипотезы с помощью критерия хи-квадрат.

Psi: Ψ ψ

Psi чем-то напоминает еврейские меноры. Я лучше всего могу их описать. Действительно.

1. Пси в нижнем регистре представляет собой обратную константу Фибоначчи. Готово и сделано.

Омега: Ω ω

Это одна из самых популярных греческих букв. Omega в верхнем регистре очень уникальна, так как выглядит как заглавная O, но нижняя часть разделена.Строчная Омега выглядит как строчная буква w.

1. Прописные буквы Omega используются в электронике и в измерительном блоке Ом, который измеряет сопротивление.

2. Омега в нижнем регистре используется в статистике, где представляет собой общий набор возможных результатов.

Это все греческие буквы. Они используются в других областях, так что поищите другие варианты использования греческого алфавита. Никогда не знаешь, может ты узнаешь что-то новое!

Греческие / еврейские / латинские символы в математике | Math Vault

$ \ alpha $ ( Строчная буква , «a» на английском языке)	Переменная для углов, уровень статистической значимости	При $ \ alpha = 0.01 $, нулевая гипотеза отклоняется.
$ \ mathrm {B} $ ( Заглавная бета , «B» на английском языке)	Бета-функция	Для всех $ x, y \ in \ mathbb {R} $, $ \ mathrm { B} (x, y) = \ mathrm {B} (y, x) $.
$ \ beta $ ( Нижний регистр бета , «b» на английском языке)	Стандартизованный коэффициент регрессии, вероятность ошибки типа II	$ \ beta $ обозначает вероятность того, что нулевая гипотеза будет принята — задана что это ложь.
$ \ Gamma $ ( Гамма в верхнем регистре , «G» на английском языке)	Гамма-функция, Гамма-распределение	Для всех $ n \ in \ mathbb {N} _ + $, $ \ Gamma ( п) = (п-1)! $.
$ \ gamma $ ( Гамма в нижнем регистре , «g» на английском языке)	Константа Эйлера – Маскерони	$ \ displaystyle \ gamma = \ lim_ {n \ to \ infty} $ $ \ left (\ frac {1} {1} + \ cdots + \ frac {1} {n} \ — \ ln n \ right) $
$ \ Delta $ ( дельта в верхнем регистре , «D» на английском языке )	Дискриминант, оператор конечных разностей, оператор Лапласа	$ \ Delta (k_1 f + k_2 g) = $ $ k_1 \ Delta f + k_2 \ Delta g $
$ \ delta $ ( дельта в нижнем регистре , «d» на английском языке)	дельта-функция Кронекера, дельта-функция Дирака	$ \ delta_ {ij} = \ begin {cases} 0 & i \ ne j \\ 1 & i = j \ end {cases} $
$ \ epsilon $, $ \ varepsilon $ ( epsilon в нижнем регистре , «e» на английском языке)	Переменная в доказательствах с ограничениями	Для любого $ \ varepsilon> 0 $ существует $ n \ in \ mathbb {N} $ такой, что $ \ displaystyle \ left \| \ frac {1} {n} \ right \| <\ varepsilon $.{\ prime} (x)} {\ Gamma (x)} $
$ \ zeta $ ( Строчная дзета , «z» на английском языке)	Дзета-функция Римана	$ \ zeta (0 ) = — \ dfrac {1} {2} $
$ \ eta $ ( Нижний регистр eta , «h» на английском языке)	Функция Дирихле eta	$ \ eta (0) = \ dfrac {1} {2} $
$ \ Theta $ ( Theta в верхнем регистре , «Th» на английском языке)	Big-Theta-нотация	$ f (n) \ in \ Theta (g (n )) $, если $ f (n) $ в конечном итоге ограничено между $ k_1 g (n) $ и $ k_2 g (n) $.
$ \ theta $, $ \ vartheta $ ( Строчная theta , «th» на английском языке)	Переменная для углов	$ \ sin (2 \ theta) = \\ 2 \ sin \ theta \ cos \ theta $
$ \ iota $ ( iota в нижнем регистре , «i» на английском языке)	Функция включения в теории множеств	$ \ iota (x) = x $
$ \ kappa $ ( Каппа в нижнем регистре , «k» на английском языке)	Кривизна	$ \ kappa = \ dfrac {1} {R} $
$ \ Lambda $ ( Лямбда в верхнем регистре , «L» на английском языке)	Набор всех логических значений в логике первого порядка	$ [\ forall x (x = x)] \ in \ Lambda $
$ \ lambda $ ( Строчная лямбда , «l» на английском языке)	Параметр в пуассоновском и экспоненциальном распределении, переменная для собственных значений	$ A \ mathbf {v} = \ lambda \ mathbf {v} $
$ \ mu $ ( нижний регистр mu , «m» на английском языке)	Среднее значение совокупности, функция Мёбиуса	$ H_0 \!: \! \ Mu_1 = \ mu_2 $
$ \ nu $ ( нижний регистр nu , «n» на английском языке)	Переменная для степени свободы	$ \ chi ^ 2 (\ nu) = $ $ \ mathrm {Gamma} \ left (\ nu / 2, 1/2 \ right) $
$ \ Xi $ ( Заглавные буквы xi , «X» на английском языке)	Исходная функция Xi Римана	$ \ Xi (-z) = \ Xi (z) $
$ \ xi $ ( Нижний регистр xi , «x» на английском языке)	Функция Римана Xi	$ \ xi (2) = \ dfrac {\ pi} {6} $
$ \ omicron $ ( Строчная omicron , «o» на английском языке)	Маленькая o-запись	$ x \ in \ omicron (x ^ 2) $
$ \ Pi $ ( Заглавная pi , « P ”на английском языке)	Оператор произведения Pi	$ \ prod_ {i = 1} ^ 5 i = 5! $
$ \ pi $ ( Пи в нижнем регистре , «p» на английском языке)	Константа Архимеда, функция счета простых чисел, доля населения	$ A = \ pi r ^ 2 $
$ \ rho $ ( Rho в нижнем регистре , «r» на английском языке)	Корреляция населения	$ H_a \!: \! \ rho> 0 $
$ \ Sigma $ ( Заглавная сигма , «S» на английском языке)	Оператор суммирования	$ \ sum_ {i = 1} ^ {10} i = 55 $
$ \ sigma $, $ \ varsigma $ ( Строчная сигма , «s» на английском языке)	Стандартное отклонение совокупности, переменная для перестановок	$ \ sigma (1) = 2, \ sigma (2 ) = 3, $ $ \ sigma (3) = 1 $
$ \ tau $ ( Тау в нижнем регистре , «t» на английском языке)	Отношение длины окружности к радиусу	$ \ tau = 2 \ pi $
$ \ mathrm {Y} $, $ \ Upsilon $ ( Прописные буквы ипсилон , «U» на английском языке)	Ипсилон-функция	$ \ Upsilon (z) = \ \ \ displaystyle \ sum_ {i = 1} ^ {\ infty} \ frac {1} {i ^ 2 + z ^ 2} $
$ \ upsilon $ ( строчная ипсилон , «u» в Английский)	Общая переменная	$ \ upsilon ^ {\ prime} (t) +2 \ up silon (t) = 3 $
$ \ Phi $ ( Заглавные буквы phi , «Ph» на английском языке)	Сопряжение золотого сечения, cdf стандартного нормального распределения	$ \ Phi = \ dfrac {1 } {\ varphi} \ около 0.618 $
$ \ phi $, $ \ varphi $ ( нижний регистр phi , «ph» на английском языке)	Золотое сечение, функция Эйлера, переменная для углов, pdf Z-распределения	$ \ varphi = \ dfrac {1+ \ sqrt {5}} {2} $
$ \ chi $ ( Строчная хи , «ch» на английском языке)	Распределение хи-квадрат, характеристика Эйлера	$ \ chi = VE + F $
$ \ Psi $ ( прописные psi , «Ps» на английском языке)	Переменная для наборов предложений	$ \ Phi \ cup \ Psi $ доказывает предложение $ \ alpha $.{\ Omega} = 1 $
$ \ omega $ ( Омега в нижнем регистре , «o» на английском языке)	Наименьший бесконечный порядковый номер, простая омега-функция	Для всех $ n \ in \ mathbb {N } $, $ n <\ omega $.

Символы и символы греческого алфавита | Математические применения

Греческий алфавит широко используется в математических и научных уравнениях, при этом широко используются такие буквы, как пси, ро, эта, мю, омега и многие другие.

Буквы и символы Включает:
Греческий алфавит
Математические символы
Математические константы
Типографические символы

Греческий алфавит широко используется для понижения различных констант и значений в научной и технической сферах.Буквы, включая омега, эта, ро, мю и многие другие, используются для обозначения целого ряда математических, научных и инженерных мер. Все, от удельного сопротивления до импеданса, проницаемости, отношения кругов и многого другого.

В греческом алфавите всего 24 буквы по сравнению с латинским алфавитом, в котором используется 26. Однако в греческом алфавите есть как заглавные, так и маленькие версии, и практически все буквы широко используются для множества различных мер.

Различные греческие буквы имеют разное значение или используются для обозначения различных мер, как указано в списке ниже.

Список знаков и символов греческого алфавита
Греческая буква	Греческий символ		Используется для обозначения
	Капитал	Малый
Альфа	Α	α	Углы, коэффициенты, постоянная затухания, коэффициент поглощения, площадь
Бета	Β	β	Углы, коэффициенты, фазовая постоянная
Гамма	Γ	γ	Комплексная постоянная распространения (cap), удельный вес, углы, электропроводность, постоянная распространения
Дельта	Δ	δ	Увеличение или уменьшение, определитель (cap), диэлектрическая проницаемость (cap), плотность, углы
Эпсилон	Ε	ε	Диэлектрическая проницаемость, диэлектрическая проницаемость, электрическая напряженность
Зета	Ζ	ζ	Координаты, коэффициенты
Эта	Η	η	Собственный импеданс, КПД, поверхностная плотность заряда, гистерезис, координаты
Тета	Θ	θ	Угловой сдвиг фаз, углы, постоянная времени, сопротивление
Йота	Ι	ι	Единичный вектор
Каппа	Κ	κ	Восприимчивость, коэффициент связи, теплопроводность
Лямбда	Λ	λ	Проницаемость (цоколь), длина волны, постоянная затухания
му	Μ	мкм	Проницаемость, коэффициент усиления (в клапанах / вакуумных трубках), приставка для микромножителя.
Nu	Ν	ν	Относительность, частота
Xi	Ξ	ξ	Координаты
Omicron	Ο	ο
Пи	Π	π	Обычно используется для 3.1416. . . .
Rho	Ρ	ρ	Удельное сопротивление, объемная плотность заряда, координаты
сигма	Σ	σ	Суммирование (крышка), поверхностная плотность заряда, комплексная постоянная распространения, электрическая проводимость, коэффициент утечки, отклонение
Тау	Τ	τ	Постоянная времени, объемное сопротивление, фазовый сдвиг, коэффициент передачи, плотность
Ипсилон	Υ	υ
Phi	Φ	φ	Скалярный потенциал (кап), магнитный поток, углы
Чи	Χ	χ	Электрическая восприимчивость, углы
фунтов на квадратный дюйм	Ψ	ψ	Диэлектрический поток, разность фаз, координаты, углы
Омега	Ом	ω	Электрическое сопротивление (цоколь), телесный угол, угловая скорость

Примечание: В алфавите используется строчная греческая буква, кроме тех случаев, когда используется обозначение (заглавная буква), где используется заглавная версия греческой буквы.

Как формировался греческий алфавит

Как всем известно, греческий алфавит с его буквами и символами насчитывает много тысяч лет.

Хотя греческий алфавит широко использовался в Греции и ее империи, алфавит и связанные с ним символы испытали влияние гораздо более ранних цивилизаций, а также в результате влияния торговли, которая имела место в Средиземноморье и за его пределами.

Одно из главных влияний на греческий алфавит оказали финикийцы.Около 750 г. до н.э. греки начали перенимать языковую систему у финикийцев, хотя на это оказали влияние минойцы и микенцы, которые были другими основными группами, с которыми древние греки контактировали.

По сути, греческий алфавит стал преемником финикийского и в конечном итоге стал греческим алфавитом с его символами, которые мы используем сегодня.

Почему в математических и научных уравнениях используются греческие буквы

Существует несколько причин, по которым для обозначения констант в уравнениях принято много греческих букв.

Во-первых, конечно, необходимо понять, что многие из наших стандартных букв широко используются, особенно для переменных: x, y, z — некоторые общие примеры, но также используются и другие.

Многие буквы греческого алфавита используются как константы в уравнениях и формулах. , Θ, а также α, β, θ и т.п. широко используются и рассматриваются как представляющие значения или константы для множества значений.

Корни использования греческих букв восходят к древнейшим философам, таким как Аристотель, Диофант и другие.Они использовали буквы греческого алфавита в качестве символов для обозначения различных переменных. Хотя более поздние цивилизации использовали свои собственные буквы, использование греческих букв, как правило, использовалось на протяжении веков — люди, как правило, использовали то, что уже было установлено.

Сегодня есть преимущества использования символов греческого алфавита. В повседневном использовании они более различимы, чем обычный алфавит, и их реже путают с языковым текстом в написанной математической работе.