Не равен знак: Математические знаки ≈ ∑ ⇒ ∈ ≤ ∞
Линейные неравенства, решение и примеры
Основные понятия
Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.
Неравенство — это алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Линейные неравенства — это неравенства вида:
- ax + b < 0,
- ax + b > 0,
- ax + b ≥ 0,
- ax + b ≤ 0,
где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.
Типы неравенств
- Строгие — используют только больше (>) или меньше (<):
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- a > b и b < a означают одно и тоже, то есть равносильны.
- Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно):
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
- Другие типы:
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Линейные неравенства: свойства и правила
Вспомним свойства числовых неравенств:
- Если а > b , то b < а. Также наоборот: а < b, то b > а.
- Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.
- Если а > b, то а + c > b+ c (и а – c > b – c).
Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.
- Если а > b и c > d, то а + c > b + d.
Если а < b и c < d, то а + c < b + d.
Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять из-за возможных исключений. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
- Если а > b и c < d, то а – c > b – d.
Если а < b и c > d, то а – c < b – d.
Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.
- Если а > b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа < nb и
Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
- Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а < b и c < d, где а, b, c, d > 0, то аc < bd.
Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие данного правила или квадратный пример: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.
- Если а > b, где а, b > 0, то
Если а < b , то
Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.
Важно знать
Два неравенства можно назвать равносильными, если у них одинаковые решения.
Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.
Свойства выше помогут нам использовать следующие правила.
Правила линейных неравенств
|
Решение линейных неравенств
Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.
Определение 1. Линейное неравенство с неизвестной переменной x имеет вид ax + b > 0, когда вместо > используется любой знак < , ≤ , ≥ , а и b — действительные числа, a ≠ 0.
Определение 2. Неравенства называют линейными с одной переменной, когда ax < c или ax > c , где x — переменная, a, c — некоторые числа.
Мы не знаем может ли коэффициент равняться нулю, поэтому: 0 * x > c и 0 * x < c можно записать в форме нестрогого неравенства: ax ≤ c, ax ≥ c . Такое уравнение принято называть линейным. Его главные различия:
- форма записи ax + b > 0 — в первом и ax > c — во втором;
- допустимость равенства нулю: a ≠ 0 — в первом, a = 0 — во втором.
Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.
Определение 3. Линейные неравенства с одной переменной x выглядят так:
- ax + b < 0,
- ax + b > 0,
- ax + b ≤ 0,
- ax + b ≥ 0,
где a и b — действительные числа. А на месте x может быть обычное число.
Равносильные преобразования
Для решения ax + b < 0 (≤, >, ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.
Алгоритм решения ax + b < 0 при a ≠ 0
- перенесем число b в правую часть с противоположным знаком,
- получим равносильное: ax < −b;
- произведем деление обеих частей на число не равное нулю.
Когда a положительное, то знак остается, если a — отрицательное, знак меняется на противоположный.
Рассмотрим пример: 4x + 16 ≤ 0.
Как решаем: В данном случае a = 4 и b = 16, то есть коэффициент при x не равен нулю. Применим вышеописанный алгоритм.
- Перенесем слагаемое 16 в другую часть с измененным знаком: 4x ≤ −16.
- Произведем деление обеих частей на 4. Меняем знак, так как 4 — положительное число: 4x : 4 ≤ −16 : 4 ⇒ x ≤ −4.
- Неравенство x ≤ −4 является равносильным. То есть решением является любое действительное число, которое меньше или равно 4.
Ответ: x ≤ −4 или числовой промежуток (−∞, −4].
При решении ax + b < 0, когда а = 0, получается 0 * x + b < 0. На рассмотрение берется b < 0, после выясняется верное оно или нет.
Вернемся к определению решения неравенства. При любом значении x мы получаем числовое неравенство вида b < 0. При подстановке любого t вместо x, получаем 0 * t + b < 0 , где b < 0. Если оно верно, то для решения подойдет любое значение. Когда b < 0 неверно, тогда данное уравнение не имеет решений, так как нет ни одного значения переменной, которое может привести к верному числовому равенству.
Числовое неравенство вида b < 0 (≤, > , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.
Рассмотрим пример: 0 * x + 5 > 0.
Как решаем:
- Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
- Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.
Ответ: промежуток (− ∞ , + ∞).
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов это:
- введение функции y = ax + b;
- поиск нулей для разбиения области определения на промежутки;
- отметить полученные корни на координатной прямой;
- определение знаков и отмечание их на интервалах.
Алгоритм решения ax + b < 0 (≤, >, ≥) при a ≠ 0 с использованием метода интервалов:
- найдем нули функции y = ax + b для решения уравнения ax + b = 0.
Если a ≠ 0, тогда решением будет единственный корень — х₀;
- начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
- определим знаки функции y = ax + b на промежутках.
Для этого найдем значения функции в точках на промежутке;
- если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если < или ≤ н — над отрицательным промежутком.
Рассмотрим пример: −3x + 12 > 0.
Как решаем:
- В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,
−6x = −12,
x = 2.
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
- Определим знаки на промежутках.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6 < 0 . Знак на промежутке является отрицательным.
- Выполним решение со знаком >. Штриховку сделаем над положительным промежутком.
По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x < 4.
Ответ: (−∞, 4) или x < 4.
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
- во время решения ax + b < 0 определить промежуток, где график изображен ниже оси Ох;
- во время решения ax + b ≤ 0 определить промежуток, где график изображается ниже Ох или совпадает с осью;
- во время решения ax + b > 0 произвести определение промежутка, где график изображается выше Ох;
- во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.
Рассмотрим пример: −5 * x − √3 > 0.
Как решаем
- Так как коэффициент при x отрицательный, данная прямая является убывающей.
- Координаты точки пересечения с Ох равны −√3 : 5.
- Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
- Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.
Ответ: (−∞, −√3 : 5) или x < −√3 : 5.
Линейные неравенства в 8 классе — это маленький кирпич, который будет заложен в целый фундамент знаний. Мы верим, что у все получится!
Чтобы ребенок чувствовал себя увереннее на сложных контрольных и улучшил оценки в школе, запишите его на уроки математики в Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Строгие и нестрогие неравенства
Например, неравенство \(x>4\) – строгое. В нем решениями будут только значения больше четверки. При этом сама четверка решением не будет! Действительно, если мы подставим в неравенство вместо икса число \(4\), получим неверное числовое неравенство \(4>4\).
То есть, в строгих неравенствах не допускается равенство правой и левой части. Поэтому они и называются строгими. Оформление решения таких неравенств показано ниже: граничная точка (в нашем случае четверка) на числовой оси не закрашена (еще говорят «выколота»), а в записи промежутка на этом значении переменной стоит круглая скобка «(».
\(x>4\)
Ответ: \(x \: ϵ \: (4;+∞)\)
Нестрогие – это неравенства со знаками сравнения \(≥\) (больше или равно) или \(≤\) (меньше или равно).
Само название знаков сравнения уже подразумевает, что здесь равенство левой и правой части допускается, и значение икса, приводящее к такому результату, решением будет.
Например, неравенство \(x≥4\) – нестрогое. И в нем решением являются не только значения больше четырех, но и сама четверка тоже. Действительно, подставив вместо икса \(4\), получим верное числовое неравенство \(4≥4\) (потому что четверка и в самом деле равна четверке).
При записи решения таких неравенств граничную точку на числовой оси закрашивают, а при записи промежутка скобку на этом значении пишут не круглую, а прямоугольную «[».
\(x≥4\)
Ответ: \(x\: ϵ\: [4;+∞)\)
Знак «не равно» в визуальном прологе?
Я не могу найти документацию по знаку «не равно» в Visual Prolog. Пожалуйста, предоставьте правильное решение этой проблемы:
class predicates
sister : (string Person, string Sister) nondeterm(o,o).
clauses
sister(Person, Sister) :-
Person [not-equal-sign] Sister,
parent(Person, Parent),
parent(Sister, Parent),
woman(Sister).
23
автор: Mateusz Piotrowski
2 ответов
Я не знаю, что вы подразумеваете под «не равно» (не объединить?), но вы можете попробовать следующее:
X \= Y
not(X = Y)
\+ (X = Y)
документацию по второму варианту, указанному Kaarel, можно найти в этот визуальный Пролог ссылка страница.
однако проблема с вашим кодом идет немного глубже. Вам нужно дождаться тестирования неравенств, пока оба термина Person и Sister не будут связаны, поэтому переставьте вещи так:
sister(Person, Sister) :-
parent(Person, Parent),
parent(Sister, Parent),
not(Person = Sister),
woman(Sister).
существует также синтаксис для оператора infix»», что означает distinct (или different). Как только два условия связаны это должно дать тот же результат, что и проверка невозможности унификации терминов, что и вышеописанная конструкция.
Неравенство — Википедия
Нера́венство в математике — отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков[1].
- Строгие неравенства
Неравенства a>b{\displaystyle a>b} и b<a{\displaystyle b<a} равносильны. Говорят, что знаки >{\displaystyle >} и <{\displaystyle <} противоположны; например, выражение «знак неравенства сменился на противоположный» означает, что <{\displaystyle <} заменено на >{\displaystyle >} или наоборот.
- Нестрогие неравенства
Русскоязычная традиция начертания знаков ⩽{\displaystyle \leqslant } и ⩾{\displaystyle \geqslant } отличается от принятой за рубежом, где обычно используются знаки ≤{\displaystyle \leq } и ≥{\displaystyle \geq }.Про знаки ⩽{\displaystyle \leqslant } и ⩾{\displaystyle \geqslant } также говорят, что они противоположны.
- Другие типы неравенств
Далее в данной статье, если не оговорено иное, понятие неравенства относится к первым 4 типам.
В элементарной математике изучают числовые неравенства. В общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы.
Связанные определения
Неравенства с одинаковыми знаками называются одноимёнными (иногда используется термин «одного смысла» или «одинакового смысла»).
Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:
- a<b<c{\displaystyle a<b<c} — это краткая запись пары неравенств: a<b{\displaystyle a<b} и b<c.{\displaystyle b<c.}
Числовые неравенства
Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных (x,y,…).{\displaystyle (x,y,\dots ).} Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные. Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство 18x<414{\displaystyle 18x<414} — алгебраическое первой степени, неравенство 2×3−7x+6>0{\displaystyle 2x^{3}-7x+6>0} — алгебраическое третьей степени, неравенство 2x>x+4{\displaystyle 2^{x}>x+4} — трансцендентное[2].
Свойства
Свойства числовых неравенств в некоторых отношениях близки к свойствам уравнений[1]:
- К обеим частям неравенства можно прибавить одно и то же число.
- От обеих частей неравенства можно отнять одно и то же число. Следствие: как и для уравнений, любой член неравенства можно перенести в другую часть с противоположным знаком. Например, из a+b<c{\displaystyle a+b<c} следует, что a<c−b.{\displaystyle a<c-b.}
- Обе части неравенства можно умножить на одно и то же положительное число.
- Одноимённые неравенства можно складывать: если, например, a<b{\displaystyle a<b} и c<d,{\displaystyle c<d,} то a+c<b+d.{\displaystyle a+c<b+d.} Неравенства с противоположными знаками можно аналогично почленно вычитать.
- Если все четыре части двух неравенств положительны, то неравенства можно перемножить.
- Если обе части неравенства положительны, то их можно возвести в одну и ту же (натуральную) степень, а также логарифмировать с любым основанием (если основание логарифма меньше 1, то знак неравенства надо изменить на противоположный).
- Другие свойства
- (Транзитивность) Если a<b{\displaystyle a<b} и b<c,{\displaystyle b<c,} то a<c{\displaystyle a<c} и аналогично для прочих знаков.
- Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный: больше на меньше, больше или равно на меньше или равно и т. д.
Решение неравенств
Если неравенство содержит символы неизвестных, то решение его означает выяснение вопроса, при каких значениях неизвестных неравенство выполняется. Примеры:
- x2<4{\displaystyle x^{2}<4} выполняется при −2<x<2.{\displaystyle -2<x<2.}
- x2>4{\displaystyle x^{2}>4} выполняется, если либо x>2,{\displaystyle x>2,} либо x<−2.{\displaystyle x<-2.}
- x2<−4{\displaystyle x^{2}<-4} не выполняется никогда (решений нет).
- x2>−4{\displaystyle x^{2}>-4} выполняется при всех x{\displaystyle x} (тождество).
Внимание: если возвести в чётную степень неравенство, содержащее неизвестные, могут появиться «лишние» решения. Пример: если неравенство x>3{\displaystyle x>3} возвести в квадрат: x2>9,{\displaystyle x^{2}>9,} то появится ошибочное решение x<−3,{\displaystyle x<-3,} не удовлетворяющее исходному неравенству. Поэтому все полученные таким образом решения следует проверить подстановкой в исходное неравенство.
Неравенства первой степени
Неравенство первой степени имеет общий формат: ax>b{\displaystyle ax>b} или ax<b,{\displaystyle ax<b,} где a≠0{\displaystyle a\neq 0} (работа со знаками ⩾{\displaystyle \geqslant } и ⩽{\displaystyle \leqslant } аналогична). Чтобы его решить, разделите неравенство на a{\displaystyle a} и, если a<0,{\displaystyle a<0,} измените знак неравенства на противоположный[3]. Пример:
- 5x−11>8x+1.{\displaystyle 5x-11>8x+1.} Приведём подобные члены: −3x>12,{\displaystyle -3x>12,} или x<−4.{\displaystyle x<-4.}
Системы неравенств первой степени
Если одно и то же неизвестное входит более чем в одно неравенство, надо решить каждое неравенство в отдельности и затем сопоставить эти решения, которые должны выполняться все вместе.
Пример 1. Из системы {4x−3>5x−52x+4<8x{\displaystyle {\begin{cases}4x-3>5x-5\\2x+4<8x\end{cases}}} получаем два решения: для первого неравенства x<2,{\displaystyle x<2,} для второго: x>23.{\displaystyle x>{2 \over 3}.} Соединяя их, получаем ответ: 23<x<2.{\displaystyle {2 \over 3}<x<2.}
Пример 2. {2x−3>3x−52x+4>8x{\displaystyle {\begin{cases}2x-3>3x-5\\2x+4>8x\end{cases}}} Решения: x<2{\displaystyle x<2} и x<23.{\displaystyle x<{2 \over 3}.} Второе решение поглощает первое, так что ответ: x<23.{\displaystyle x<{2 \over 3}.}
Пример 3. {2x−3<3x−52x+4>8x{\displaystyle {\begin{cases}2x-3<3x-5\\2x+4>8x\end{cases}}} Решения: x>2{\displaystyle x>2} и x<23,{\displaystyle x<{2 \over 3},} они несовместимы, поэтому исходная система не имеет решений.
Неравенства второй степени
Общий вид неравенства второй степени (называемого также квадратным неравенством):
- x2+px+q>0{\displaystyle x^{2}+px+q>0} или x2+px+q<0.{\displaystyle x^{2}+px+q<0.}
Если квадратное уравнение x2+px+q=0{\displaystyle x^{2}+px+q=0} имеет вещественные корни x1,x2,{\displaystyle x_{1},x_{2},} то неравенство можно привести к виду соответственно:
- (x−x1)(x−x2)>0{\displaystyle (x-x_{1})(x-x_{2})>0} или (x−x1)(x−x2)<0.{\displaystyle (x-x_{1})(x-x_{2})<0.}
В первом случае x−x1{\displaystyle x-x_{1}} и x−x2{\displaystyle x-x_{2}} должны иметь одинаковые знаки, во втором — разные. Для окончательного ответа надо применить следующее простое правило[4].
Квадратный трёхчлен x2+px+q{\displaystyle x^{2}+px+q} с разными вещественными корнями отрицателен в интервале между корнями и положителен вне этого интервала. |
Если оказалось, что у уравнения x2+px+q=0{\displaystyle x^{2}+px+q=0} вещественных корней нет, то его левая часть сохраняет один и тот же знак при всех x.{\displaystyle x.} Поэтому исходное неравенство второй степени либо является тождеством, либо не имеет решений (см. ниже примеры[5]).
Пример 1. −2×2+14x−20>0.{\displaystyle -2x^{2}+14x-20>0.} Разделив на −2,{\displaystyle -2,} приведём неравенство к виду: x2−7x+10<0.{\displaystyle x^{2}-7x+10<0.} Решив квадратное уравнение x2−7x+10=0,{\displaystyle x^{2}-7x+10=0,} получаем корни x1=2;x2=5,{\displaystyle x_{1}=2;x_{2}=5,} поэтому исходное неравенство равносильно такому: (x−2)(x−5)<0.{\displaystyle (x-2)(x-5)<0.} Согласно приведенному выше правилу, 2<x<5,{\displaystyle 2<x<5,} что и является ответом.
Пример 2. −2×2+14x−20<0.{\displaystyle -2x^{2}+14x-20<0.} Аналогично получаем, что x−2{\displaystyle x-2} и x−5{\displaystyle x-5} имеют одинаковые знаки, то есть, согласно правилу, либо x<2,{\displaystyle x<2,} либо x>5.{\displaystyle x>5.}
Пример 3. x2+6x+15>0.{\displaystyle x^{2}+6x+15>0.} Уравнение x2+6x+15=0{\displaystyle x^{2}+6x+15=0} не имеет вещественных корней, поэтому левая часть его сохраняет знак при всех x.{\displaystyle x.} При x=0{\displaystyle x=0} левая часть положительна, поэтому исходное неравенство есть тождество (верно при всех x{\displaystyle x}).
Пример 4. x2+6x+15<0.{\displaystyle x^{2}+6x+15<0.} Как и в предыдущем примере, здесь левая часть всегда положительна, поэтому неравенство не имеет решений.
Аналогично, разложением на множители, можно решать неравенства высших степеней. Другой способ — построить график левой части и определить, какие знаки она имеет в различных интервалах[6].
Некоторые известные неравенства
Ниже приведены практически полезные неравенства, тождественно выполняющиеся, если неизвестные попадают в указанные границы[7].
- (1+x)n⩾1+nx,{\displaystyle (1+x)^{n}\geqslant 1+nx,} где x⩾−1,n{\displaystyle x\geqslant -1,n} — натуральное число.
- |a+b|⩽|a|+|b|{\displaystyle |a+b|\leqslant |a|+|b|}
- См. следствия этого неравенства в статье Абсолютная величина.
Знаки неравенства в языках программирования
Символ «не равно» в разных языках программирования изображается по-разному.
| Символ | Языки |
|---|---|
| != | C, Java, PHP, Python |
| <> | Basic, Pascal |
| ~= | Lua |
| /= | Haskell, Fortran, Ada |
| # | Modula-2, Oberon |
Коды знаков неравенств
См. также
Примечания
- ↑ 1 2 Неравенства // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 999.
- ↑ Справочник по элементарной математике, 1978, с. 177.
- ↑ Справочник по элементарной математике, 1978, с. 178.
- ↑ Элементарная математика, 1976, с. 217—222.
- ↑ Справочник по элементарной математике, 1978, с. 180—181.
- ↑ Элементарная математика, 1976, с. 212—213, 219—222.
- ↑ Справочник по элементарной математике, 1978, с. 174—176.
Литература
- Беккенбах Э. Ф. Неравенства. — М.: Мир, 1965.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Харди Г. Г., Литлвуд Д. И., Полиа Д. Неравенства. — М.: Иностранная литература, 1948.
План-конспект занятия по математике (подготовительная группа): НОД по ФЭМП Знакомство с знакми «больше, меньше, равно»
Государственное бюджетное дошкольное образовательное учреждение
Детский сад №1 комбинированного вида
Невского района Санкт-Петербурга
Конспект непрерывной образовательной деятельности
по формированию элементарных математических понятий
Знакомство с математическими знаками
больше, меньше, равно»
для детей подготовительной группы.
Воспитатель: Муромцева Е.А.
Санкт-Петербург, 2020
Цель: знакомство детей со знаками больше, меньше, равно
Задачи:
Образовательные — освоение знаковой системы соотношений между числами
Развивающие — Закрепить порядок чисел в числовом ряду, умение называть число на один меньше или больше. Закрепить умение называть соседей чисел
Воспитательные — воспитание выдержки, развитие внимания.
Материалы и обородувание: раздаточные карточки с цифрами от 1 до 6, демонстрационные знаки больше, меньше , равно, изготовленных из картона в виде крокодилов с открытой пастью, магнитные карточки с фруктами. Демонстрационный материал: две группы кружков по 4 и 5 разного цвета, знаки «больше, меньше, равно», наборное полотно, мяч, указка, две группы кружков по 4 и 5 разного цвета, 1/2 альбомного листа, разделенного пополам, знаки «больше, меньше, равно», карточки для самостоятельной работы, простой карандаш.
Методы: словесный, наглядный
Ход занятия:
Воспитатель: Ребята, мы сегодня с вами познакомимся с математическими знаками «больше, меньше, равно». Посмотрите на доску, как они обозначаются. На что похожи эти знаки? Варианты детей. Я согласна с вами. Больше они похожи на пасть крокодила. Посмотрите, к нам приплыли крокодильчики. Каждый крокодильчик плывет с открытой пастью к тем предметам, которых больше. А если количество предметов одинаковое, то крокодильчики плывут вместе с закрытой пастью. Садитесь за столы, ребята перед вами лежат геометрические фигуры и полотно (1/2 альбомного листа, разделенного пополам). Выложите слева 4 квадрата, а справа 5 кругов.
Воспитатель дублирует работу детей на магнитной доске
А теперь давайте сравним квадраты и круги. Чего больше? (кругов) Как вы узнали, что кругов больше? (посчитали) Значит у нас квадратов меньше, чем кругов. Каким же знаком мы укажем неравенство фигур? Поставьте между своими цифрами нужный знак. Давайте прочитаем нашу запись: 4 меньше 5. А теперь добавьте два квадрата слева. Каких фигур больше? Каким знаком укажем? Давайте проговорим: 6 больше 5. А теперь прибавьте один круг справа. Сколько квадратов? Сколько кругов? Каких фигур меньше? Правильно. Одинаково. 6=6. Между цифрами ставим знак равенства.
Физминутка
Игра «Сделай движение на одно меньше (больше) »
Дети встают в круг, а воспитатель говорит: прыгните на один раз больше, чем я хлопну в ладоши (хлопаю в ладоши 6 раз), сделайте приседаний на одно меньше, чем я хлопну в ладоши и т.д.
Самостоятельная работа
Молодцы! А сейчас садитесь за столы. Посмотрите, перед вами лежат карточки и математические знаки. Расставьте правильно знаки «больше», «меньше», «равно»
Дети самостоятельно ставят знаки «больше», «меньше», «равно»
Воспитатель проверяет работы детей.
Дидактическая игра «Соседи». Воспитатель бросает мяч и называет число, ребенок называет соседнее большее или меньшее, в соответствии с заданием.
Математические задачки
— Что больше – 3 стула или 4 кровати?
— Чего меньше – 5 яблок или 2 груши?
— Чего больше – 6 конфет или 6 пряников?
Рефлексия: Как обозначаются знаки больше, меньше, равно? На что они похожи? Где эти знаки ставятся?
Все Символы | Знаки | Коды | HTML | ||
| ➕ | ➕ | Плюс жёлтого цвета |
| ➖ | ➖ | Минус синего цвета |
| ➗ | ➗ | Разделить зеленого цвета |
| ❌ | ❌ | Умножить красного цвета |
| − | − | Минус (Символ html) |
| + | + | Плюс (Символ html) |
| × | × | Умножить (Символ html) |
| ÷ | ÷ | Разделить (Символ html) |
| ± | ± | Плюс-минус |
| < | < | Меньше |
| > | > | Больше |
| ≤ | ≤ | Меньше или равно |
| ≥ | ≥ | Больше или равно |
| π | π | Пи |
| √ | √ | Корень квадратный |
| ∡ | ∡ | Корень квадратный |
| ∢ | ∢ | Корень квадратный |
| ∠ | ∠ | Угол |
| ∛ | ∛ | |
| ∜ | ∜ | |
| ⁄ | ⁄ | Слэш, дробная черта |
| ¬ | ¬ | Отрицание |
| ° | ° | Градус |
| ∼ | ∼ | Оператор тильда |
| ≅ | ≅ | Геометрическая эквивалентность |
| ≈ | ≈ | Приблизительное равенство |
| ≠ | ≠ | Не равно |
| ≡ | ≡ | Тождественное равенство |
| Математические Дроби символы коды HTML | ||
| % | % | Простая дробь «ноль на ноль» |
| ¼ | ¼ | Дробь одна четвертая |
| ½ | ½ | Дробь одна вторая |
| ¾ | ¾ | Дробь три четвертых |
| ⅓ | ⅓ | Дробь одна третья |
| ⅔ | ⅔ | Дробь две третих |
| ⅕ | ⅕ | Дробь одна пятая |
| ⅖ | ⅖ | Дробь две пятых |
| ⅗ | ⅗ | Дробь три пятых |
| ⅘ | ⅘ | Дробь четыре пятых |
| ⅙ | ⅙ | Дробь одна шестая |
| ⅚ | ⅚ | Дробь пять шестых |
| ⅛ | ⅛ | Дробь одна восьмая |
| ⅜ | ⅜ | Дробь три восьмых |
| ⅝ | ⅝ | Дробь пять восьмых |
| ⅞ | ⅞ | Дробь семь восьмых |
| Другие математические символы коды HTML | ||
| ¹ | ¹ | Верхний индекс «1» |
| ² | ² | Верхний индекс «2» |
| ³ | ³ | Верхний индекс «3» |
| ∞ | ∞ | Бесконечность |
| ∝ | ∝ | Пропорционально |
| ⊥ | ⊥ | Ортогонально, перпендикуляр |
| ∴ | ∴ | Следовательно |
| ƒ | ƒ | Функция |
| ∫ | ∫ | Интеграл |
| ∂ | ∂ | Частный дифференциал |
| ∇ | ∇ | Оператор набла |
| ∀ | ∀ | Для всех |
| ∃ | ∃ | Существует |
| ∏ | ∏ | Знак произведения |
| ∑ | ∑ | Сумма последовательности |
| ∧ | ∧ | Логическое И (конъюнкция) |
| ∨ | ∨ | Логическое ИЛИ (дизъюнкция) |
| ∅ | ∅ | Пустой набор = диаметр |
| ∈ | ∈ | Принадлежит |
| ∉ | ∉ | Не принадлежит |
| ∋ | ∋ | Содержит |
| ∩ | ∩ | Пересечение |
| ∪ | ∪ | Объединение |
| ⊂ | ⊂ | Является подмножеством |
| ⊃ | ⊃ | Является надмножеством |
| ⊄ | ⊄ | Не является подмножеством |
| ⊆ | ⊆ | Является подмножеством либо эквивалентно |
| ⊇ | ⊇ | Является надмножеством либо эквивалентно |
Не равно
Пропустить навигацию
Найдите свой местный ADL
Twitter
Facebook
LinkedIn
Instagram
YouTube
]]]]]]]]>]]]]]]>]]]]>]]> Логотип ADL — главная страница веб-сайтаАнтидиффамационная лига
- Кто мы есть
- Что мы делаем
- Образование
- Исследования и инструменты
- Новости
- Действовать
- Способы дать
Развернуть поиск
Поиск
Пожертвовать
Основная навигация Нижний заголовок
Кто мы есть
Узнай, кто мы
- Наша миссия
- Наши ценности
- Наша история
- Официальные заявления
- Годовые отчеты и финансовая информация
- Наша организация
- Ваш местный офис ADL
- Подписные программы
- Центры исследований и защиты интересов
- Наше руководство и персонал
- Наш совет директоров
- Партнерские организации
- Свяжитесь с нами
- Карьера в ADL
Что мы делаем
Узнайте, что мы делаем
- Борьба с антисемитизмом
- Антисемитизм в США
- Антисемитизм во всем мире
- Боритесь с ненавистью и защищайте сообщества
- Экстремизм, терроризм и фанатизм
- Киберхат
- Преступления на почве ненависти
- Безопасность сообщества
- Противодействовать дискриминации и обеспечивать правосудие
- Религиозная свобода
- Свободная речь
- Раса и расовая справедливость
- Реформа уголовного правосудия
- Равенство в образовании
- Справедливость женщин
- Право голоса
- Права ЛГБТК
- Права иммигрантов и беженцев
- Встаньте за Израиль
- Пропаганда и образование в Израиле
- Антиизраильская деятельность и BDS
- Внутренние израильские проблемы
- Продвигайте респектабельные школы и сообщества
- Антибактериальное образование
- Предотвращение издевательств и киберзапугивания
- Межконфессиональные и межгрупповые отношения
- Борьба с антисемитизмом
Образование
Исследуйте образование
- Программы и обучение борьбе с предвзятостью
- Институт мира различий®
- Нет места ненависти®
- Слова к действию
- Программы запугивания и киберзапугивания
- Просвещение о Холокосте
- Уроки
- Книжное дело: детская литература
- Книга месяца
- Инструменты и стратегии защиты от смещения
- Ресурсы по издевательствам / киберзапугиванию
- Застольный разговор: семейные разговоры
- Беседы Розалинды в классе
- Часто задаваемые вопросы о раннем детстве
- Образовательный блог
- Вебинары и подкасты
- Программы и обучение борьбе с предвзятостью
Исследования и инструменты
Изучите исследования и инструменты
- ADL Tracker антисемитских инцидентов
- Краткая база данных Amicus
- Hate on Display ™ База данных символов ненависти
- Библиотека ресурсов
- ADL Latinx
- ADL H.ЕСТЬ. карта
- Карта ADL с преступлениями на почве ненависти
Новости
Исследуйте Новости
- Пресс-центр
- Пресс-релизы / заявления
- Редакторы
- Просмотр СМИ
- ADL в новостях
- Контакты для прессы
- Блог ADL
- Письма
- Статьи
- Рассказы
- Пресс-центр
Действовать
Изучить Принять Действия
- Присоединяйтесь к сети молодых лидеров ADL
- Присоединяйтесь к нам в борьбе с ненавистью навсегда
- Свяжитесь с вашим местным офисом ADL
- Принесите ADL в вашу школу или сообщество
- Сообщить об инциденте
- Будьте услышанными в Конгрессе
Способы дать
Изучите способы отдавать
- Дать сейчас
- Ежемесячная поддержка работы ADL
- Выполните свое обещание перед ADL
- Планируемые пожертвования, наследие и пожертвования
- Пожертвовать ADL с помощью криптовалюты
- Дарить в честь или в память
- Отправить подарочную карту по электронной почте
- Поддержите ADL через свой фонд, рекомендованный донорами
- Подарите акции ADL
- Поддержите ADL с помощью денежного перевода
- Связаться с нами
- Карьера
- Подписка на новости
- видео
- политика конфиденциальности
Развернуть поиск
Поиск
- Поделиться в Twitter
- Поделиться через Facebook
- Поделиться через Pinterest
- Поделиться по электронной почте
]]]]]]]]>]]]]]]>]]]]>]]> Логотип ADL — главная страница веб-сайтаАнтидиффамационная лига
Перейти наверх
Развернуть мобильное социальное меню
Расширьте мобильный поиск
Как вставить почти равный (≈) в Word
Google│Юникод│Рукописный вводУравнение│Символ
При вставке уравнения в файл Word вам часто может потребоваться использовать знак « почти равно (≈) » или знак « не равно (≠) » в формуле.Есть много разных способов вставить эти знаки.
1. Google
Первый способ — найти в Интернете знак « почти равно » или « не равно », а затем скопировать вставку в файл Word, если у вас есть доступ в Интернет.
2. Юникод
Второй метод относительно прост, но вы должны запомнить Unicode для этих знаков: 2248 для знака « почти равно » и 2260 для знака « не равно ».Если вы знаете эти символы Юникода, выполните следующие действия:
Введите 2248 (или 2260), удерживая клавишу « Alt », затем нажмите на клавиатуре букву « X », чтобы вставить знак « почти равно (или не равно) ».
3. Почерк
В текстовый документ можно вставить почти все математические знаки с рукописным вводом.
Шаг 1. Щелкните вкладку « Вставить » на ленте;
Шаг 2: Щелкните маленький треугольник сразу после команды « Equation »;
Шаг 3: Выберите « Ink Equation » из раскрывающегося списка;
Шаг 4: Напишите знак « почти равно », перемещая курсор мыши или пальцем, если у вас сенсорный экран, затем нажмите « Вставьте » для завершения.
4. Метод уравнения
Вы можете вставить знак « почти равно » аналогично вставке числа пи (π) в текстовый файл.
Шаг 1. Щелкните вкладку « Вставить » на ленте;

Шаг 2: Щелкните « Equation » в разделе « Symbols »;

Шаг 3. На вкладке « Design » на ленте вы увидите знак « почти равно (≈) » в разделе « символов ».
Шаг 4: Щелкните по нему, чтобы вставить « ≈ » в текстовый файл.
5. Символьный метод
Вы также можете вставить знак « почти равно », выполнив те же действия, чтобы вставить галочку в файл Word.
Шаг 1. Щелкните вкладку « Вставить » на ленте;

Шаг 2: щелкните « Символ » в разделе « Символы », затем щелкните « Дополнительные символы » в раскрывающемся списке;
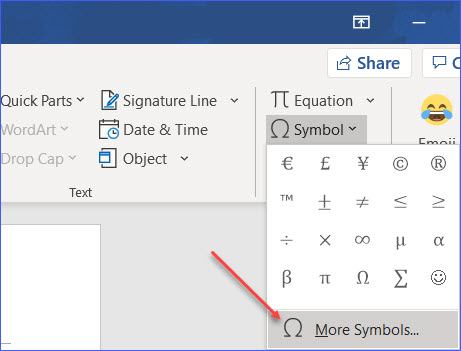
Шаг 3. Выберите « Symbol » в поле « Font » и переместите полосу прокрутки вниз, чтобы найти символ «≈»;
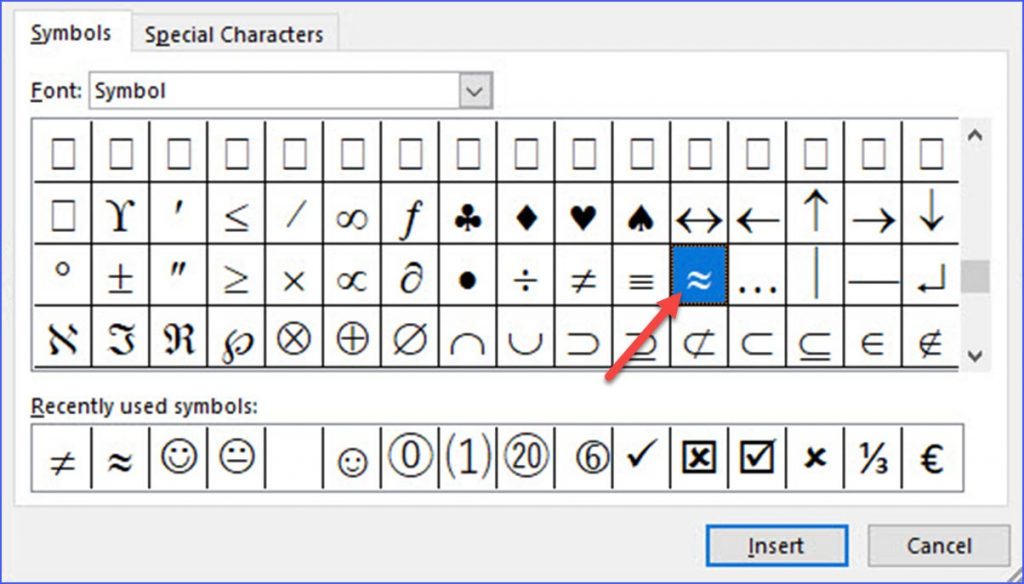
Шаг 4: Щелкните по нему и нажмите « Insert » внизу, затем нажмите « Close » для завершения.
Quick-R: Операторы
Бинарные и логические операторы
R покажутся программистам очень знакомыми. Обратите внимание, что бинарные операторы работают с векторами и матрицами, а также со скалярами.
Арифметические операторы
| Оператор | Описание |
| + | дополнение |
| — | вычитание |
| * | умножение |
| / | отдел |
| ^ или ** | возведение в степень |
| x %% y | (x mod y) 5 %% 2 составляет 1 |
| x% /% y | целочисленное деление 5% /% 2 равно 2 |
Логические операторы
| Оператор | Описание |
| < | менее |
| <= | меньше или равно |
| > | больше |
| > = | больше или равно |
| == | в точности равно |
| ! = | не равно |
| ! X | Не x |
| x | г | x OR y |
| x & y | x AND y |
| ИСТИНА (x) | проверить, истинно ли X |
# Пример
x <- c (1:10)
x [(x> 8) | (x <5)]
# дает 1 2 3 4 9 10
# Как это работает
x <- c (1:10)
x
1 2 3 4 5 6 7 8 9 10
x> 8
FFFFFFFFTT
x <5
TTTTFFFFFF
x> 8 | x <5
T T T T F F F F F T T T
x [c (T, T, T, T, F, F, F, F, T, T)]
1 2 3 4 9 10
Идем дальше
Чтобы попрактиковаться в работе с логическими операторами в R, попробуйте бесплатную первую главу с условными выражениями этого интерактивного курса.
.