Отличие математики от алгебры: Чем алгебра отличается от математики?
Отличия алгебры от арифметики
Алгебра (так же, как и арифметика) занимается нахождением решений различных вопросов, относящихся к числам. Но между этими двумя науками есть существенная разница:
- Алгебра имеет дело не с числами, а с буквами, которые могут обозначать какие угодно числа.
- В арифметике мы стараемся найти решение только одного данного вопроса с известными определенными числами. В алгебре — найти общее решение всех вопросов одного рода, какие бы числа не были даны.
Чтобы выяснить, что такое общее решение численного вопроса, решим задачу:
Два путешественника в одно и то же время выходят навстречу друг другу из двух городов, находящихся на расстоянии 240 километров. Первый проходит в день 25 километров, второй 35 километров. Через сколько дней после своего отправления они встретятся?
Каждый день они приближаются друг к другу на
25 + 35 = 60 километров.
Следовательно, они пройдут весь разделяющий их путь и встретятся через
240 : 60 = 4 дня.
Предположим теперь, что требуется решить ту же задачу, но не над тремя данными числами 240, 25 и 25 километров, а над какими угодно числами. Это часто делается для того, чтобы решение вопроса имело более общее значение, то есть годилось бы для всех одинакового рода задач, какие бы целые или дробные числа не были даны. В таком случае мы уже не можем обозначать данные величины цифрами, имеющими одно известное числовое значение, а должны пользоваться какими-нибудь другими знаками, под которыми можно было бы подразумевать какие угодно числа. За такие знаки берут буквы латинского алфавита.
Например, назовем число километров между двумя городами буквой a, количество километров, проходимых в день первым путешественником, буквой b, а вторым — c.
Решая задачу в этом общем виде, найдем, что оба путешественника каждый день приближаются друг к другу на
b + c километров
и, следовательно, встретятся через столько дней, сколько раз сумма b + c километров заключается в километрах разделяющего их пути, то есть через дней. Полученное выражение представляет общее решение данного вопроса. Подставив вместо букв числа и произведя действия, найдем прежний ответ:
Полученное выражение представляет общее решение данного вопроса. Подставив вместо букв числа и произведя действия, найдем прежний ответ:
Буквенное или общее решение имеет следующие преимущества перед числовым или частным решением:
- Оно пригодно не для одной предложенной задачи, а для всех однотипных задач, какие бы числа в них не были даны. Например, если вместо 240, 25 и 35 даны числа 360, 20 и 40, то, подставив их в полученное выражение вместо a, b, и c, найдем, что искомое число дней равно
и так далее. - Из буквенного выражения
ясно видно, какие действия и в каком порядке надо совершить над данными величинами для получения искомого ответа. - Легко заметить, что при решении вопросов, подобных данному, имеет существенное значение не
именование
предметов или понятий, данных в задаче, но количественная их величина, а потому прямо переходим к тому, что нашу задачу можно обобщить.
Например, два предмета одновременно начинают двигаться из двух мест, находящихся на расстоянии a единиц длины (всё равно каких: метры, километры, футы и т. д.). Первый предмет проходит в каждую единицу времени (сутки, час, секунду) b, а второй c таких единиц длины. Через сколько единиц времени они встретятся? Решение, очевидно, будет прежнее: через единиц времени.
Эта запись называется общей формулой, она дает нам возможность любую новую задачу с подобными условиями решить без повторения рассуждений — одним вычислением.
Итак, алгебра имеет целью находить общие решения вопросов, относящихся к числам, а также обобщать эти вопросы.
Кроме того, алгебра занимается тем, чтобы эти общие решения представлять в наиболее простом и ясном виде, также она учит, как преобразовывать одно буквенное выражение в другое, тождественное с ним, то есть в такое, которое остается равным первому при каких угодно числах.
Алгебра – основные понятия и формулы. Готовимся к ЕГЭ по Математике
В школьном курсе алгебры не так уж много теории. Намного больше практики, то есть секретов и приемов решения задач. Хороший репетитор-математик вряд ли будет читать вам на каждом уроке длинные лекции. Он скажет: «Смотри, как решаются такие задачи!»
И все-таки минимальное знание теории необходимо. Основные понятия и формулы надо знать наизусть.
Например, что такое квадратный корень из неотрицательного числа?
Что такое модуль числа?
Для каких чисел существуют логарифмы?
Чем действительные числа отличаются от рациональных?
Как узнать, что число делится на 11?
На этой странице – все основные темы и понятия алгебры, необходимые учащимся 10-11 класса. И еще – полезная информация о том, как считать быстро и без калькулятора и как легко запоминать формулы.
Числовые множества
Делимость чисел
Правила округления чисел
Таблица квадратов натуральных чисел и формулы сокращенного умножения
ЕГЭ без ошибок. Считаем быстро и без калькулятора
Считаем быстро и без калькулятора
Как запоминать формулы
Основы логики. Система условий, совокупность условий
Квадратный корень
Корни и степени
Логарифмы
Модуль числа
Число e
Проверь себя. Помнишь ли ты основные понятия алгебры?
— Арифметический квадратный корень из числа a — это такое неотрицательное число, квадрат которого равен a.
— Определение модуля числа:
— Что такое ? Запомним:
— Знаешь ли ты, что корни второй, третьей, четвертой, пятой, n-ной степени можно записывать просто как степени? И это намного удобнее. Например,
Напомним, что корень третьей степени из а – такое число, при возведении которого в третью степень получается число а.
Аналогично, корень четвертой степени из а – такое неотрицательное число, при возведении которого в четвертую степень получается число а.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a , чтобы получить b.
При этом
Что такое арифметика и чем она отличается от математики?
С одной стороны это очень простой вопрос. С другой, школьники, да и многие взрослые, часто путают арифметику и математику и толком не знают в чем же разница между этими двумя предметами. Математика — это наиболее обширное понятие, которое включает в себя любые действия с числами. Арифметика же лишь один из разделов математики. К арифметике относятся знакомство с цифрами, простой счет и операции с числами. Раньше в школах уроки назывались именно арифметикой и лишь со временем стали носить название математика, которая плавно перетекает в алгебру. По сути алгебра начинается тогда, когда в примерах появляются неизвестные числа и вместо них используются буквы. То есть по-простому операции с x и y.
Термин «арифметика» произошел от греческого слова «arithmos», что означает «число». В 14-15 веках данный термин переводился в Англии не совсем верно — «the metric art», что по сути означало «метрическое искусство», подходящее больше для геометрии, нежели простого счета и несложных действий с числами.
Одна из причин, почему в школах не используется понятие «арифметика» заключается в том, что даже на уроках в начальных классах помимо цифр изучают также геометрические формы и единицы измерения (сантиметр, метр и т.д.), а это уже выходит за пределы обычного счета. Тем не менее, обучение ментальной арифметике происходит в жизни ребенка в какой-то степени само собой, в процессе знакомства с окружающим миром. Термин «ментальная арифметика» означает умение считать в уме. Согласитесь, каждый из нас в какой-то момент жизни учится этому и не только благодаря школьным урокам.
Сегодня есть целые методики для развития у детей навыков скоростного счета в уме. Например, особенно популярно древнее Абакус обучение, в основе которого лежит умение считать на специальных счетах (отличаются от обычных с десятками). Abacus в переводе с английского и есть «счеты», потому и название методики звучит так же. Японцы же эту методику называют Соробан обучение, т.к. на их языке «счеты» называются именно «soroban».
Например, особенно популярно древнее Абакус обучение, в основе которого лежит умение считать на специальных счетах (отличаются от обычных с десятками). Abacus в переводе с английского и есть «счеты», потому и название методики звучит так же. Японцы же эту методику называют Соробан обучение, т.к. на их языке «счеты» называются именно «soroban».
В арифметике используются четыре элементарные операции — сложение, вычитание, умножение и деление. Причем неважно целые числа используются в примере или же десятичные и дроби. Знакомить ребенка с цифрами можно еще с раннего детства, причем делать это непринужденно и в игре. В этом родителям поможет не только воображение, но и множество специальных развивающих материалов, найти которые можно в любом магазине.
По современным требованиям к первому классу ребенок должен уже считать минимум в пределе десяти (а лучше до 20), а также осуществлять со знакомыми цифрами основные операции — складывать их и вычитать. Важно также, чтобы ребенок мог сравнивать, какое из чисел больше, какое меньше, а какие числа равны. Таким образом, можно сказать, что именно арифметику ребенок должен знать еще до поступления в школу.
Таким образом, можно сказать, что именно арифметику ребенок должен знать еще до поступления в школу.
Такие требования предъявляются не только в России, но и во всем мире, т.к. темп жизни ускоряется, а объем знаний ежедневно увеличивается. То, что достаточно было знать в школьной программе еще 20-30 лет назад, сегодня занимает не более 50% преподаваемой учителями информации. Как бы там ни было, арифметика всегда останется основой основ для изучения цифр и счета, а также первоначальным уровнем математики, без которого невозможно изучить более сложные задания и умения.
В чём отличие алгебры от геометрии?
Примитивно. «Врагу» надо оставлять число камней кратное шести. Естественно, что всегда выигрывает первый. На первом ходе достаточно взять четыре камушка. Более интересно: какое максимальное количество камней можно забрать на первом ходе?
У меня получилось 262144. Кто больше?
Готовые домашние задания по математике 4 класс, авторы Юдина и Захарова, можно бесплатно скачать на сайте book. 2 — 4x + 3
2 — 4x + 3
Парабола, устремлённая вверх, но в минимальных своих значениях (когда х-квадрат меньше 4х+3) имеет отрицательное значение ординаты.
И в таком варианте однозначно видим, что меньше (когда кусочек параболы ниже горизонтальной оси) — это вариант 3.
Но вот для правильного ответа (когда функция забралась выше), необходимо выбрать
ПРАВИЛЬНЫЙ ОТВЕТ = Вариант 1
Пусть дана прямая y=kx+b. И пусть дана точка M(x,y). Необходимо написать уравнение пямой, перпендикулярной данной прямой. Коэффициент k1 искомой прямой равен k1=-1/k. Далее в искомое уравнение прямой подставим координаты точки M. И найдем значение b .
Например пусть дана прямая y=2x+6. M(5,3). Запишем уравнение прямой, перпендикулярной данной. K1=-1/2. Подставляем координаты точки M, получим
K1=-1/2. Подставляем координаты точки M, получим
3=-1/2×5+b.
3=-2,5+b
b=3+2,5
b=5,5.
Тогда искомое уравнение прямой имеет вид y=-1/2x+5,5.
Дальше переносим все с иксами влево, без иксов вправо. Получаем 24х=24+63+33 (при первом вычислении у вас 63 превратилось в 6 почему-то).
Дальше 24х=120
И в итоге х=5
Собственно, и все огроменное решение. Берем учебник и бежим повторять алгебру.
Что такое алгебра? Простыми словами о сложной науке
С 5-го класса средней школы появляется предмет алгебра. Это такая наука, которая требует серьезного изучения. В этой статье приведены простыми словами объяснения, что такое алгебра и зачем она нужна человеку.
Это такая наука, которая требует серьезного изучения. В этой статье приведены простыми словами объяснения, что такое алгебра и зачем она нужна человеку.
Что это за наука
Алгебра – это не отдельная наука, а раздел математики. В ней изучаются действия над величинами. То есть каждому школьнику предстоит проводить различные вычисления, преобразования над числами, переменными. Что такое алгебра, если выразиться простыми словами? Представьте себе арифметику, где даны, например, дроби. Эти дроби нужно сложить. Как это сделать, подсказывает определенное правило: приводим их к общему знаменателю, затем нужно сделать расчет.
Также можно привести пример с простыми задачками про собранные и съеденные яблоки (сколько было и сколько осталось). Но алгебра более сложная, чем арифметика.
Какие темы относятся к алгебре
Рассмотрим, какие задачи решает алгебра:
- определение значений величин;
- решение уравнений;
- работа с дробями, числами, целыми выражениями;
- построение графиков;
- нахождение неизвестных переменных;
- доказательство теорем;
- решение неравенств;
- преобразование выражений;
- нахождение производных, интегралов.

Этот раздел математики достаточно сложен. Еще с древних времен известные ученые создавали законы, формулы, теоремы, основываясь на жизненном опыте. Недаром математика считается не просто точной наукой, но и мистической.
Зачем она нужна
Алгебра – это поиск решения и анализ той или иной задачи. Допустим, нужно раскрыть скобки в некоем уравнении, затем решить его. Находим величину неизвестной переменной «икс» (Х). Чтобы проверить, правильно ли решена задача, следует решить это уравнение другим способом: не раскрывать скобки, а решить каждое выражение по отдельности. Таким образом находятся корни уравнения, которые должны иметь те же значения, что и при раскрытии скобок.
Так зачем нужна алгебра? Она учит логическому мышлению, требует тренировки памяти, внимательности. Люди с аналитическим складом ума чаще всего прекрасно разбираются в науке. Алгебра нужна тем, кто собирается поступать в технические, экономические вузы.
В жизни она тоже может пригодиться. Например, чтобы определиться в магазине, по какой цене и в какой объеме выгоднее брать товар. Нужно произвести мысленно подсчеты. Кроме того, зачастую нам приходится считать проценты и переводить их в числа. Допустим, подоходный налог 13%. Какую сумму денег выдадут на руки, можно легко просчитать.
Например, чтобы определиться в магазине, по какой цене и в какой объеме выгоднее брать товар. Нужно произвести мысленно подсчеты. Кроме того, зачастую нам приходится считать проценты и переводить их в числа. Допустим, подоходный налог 13%. Какую сумму денег выдадут на руки, можно легко просчитать.
Какие науки применяют алгебру
Мы с вами разобрались, что такое алгебра, и чем она может быть полезна. Теперь рассмотрим, какие же науки не обходятся без нее.
Вспомним, что она является не самостоятельной дисциплиной, а всего лишь разделом математики. А математика подразделяется на арифметику (изучается в младших классах общеобразовательной школы) и на геометрию (изучают в средней школе). Почему они взаимосвязаны? Дело в том, что арифметика – это очень простые вычисления: сложение, вычитание, умножение и деление. Это все пригодится в дальнейшем обучении.
Что касается геометрии, то она изучает пространственные структуры. То есть речь идет о различных вычислениях у фигур, линий, в пространственных телах.
Без алгебры не могут существовать:
- физика;
- химия;
- информатика;
- черчение;
- экономика.
Даже некоторые гуманитарные науки не обходятся без нее, например социология.
Как успешно освоить
К сожалению, алгебра – это очень сложный предмет, впрочем, как и математика в целом. Поэтому нужно серьезно отнестись к учебе. С первых дней ее изучения (арифметика начинается в 1 классе) нужно начинать осваивать каждый урок, запоминать наизусть все, что необходимо. Если что-то пропустить, то в будущем могут быть проблема с изучением нового материала.
Математика – это своего рода цепочка из звеньев: начинается с простого, а заканчивается сложным. И так постепенно. Поэтому важно не пропускать ни один материал. Лучше несколько раз проверить себя, закрепить изученную тему.
Далее при изучении алгебры следует постоянно тренировать память. Нужно запоминать различные правила и свойства. Например, надо усвоить, что при раскрытии скобок учитываются знаки: «минус на минус дает плюс», а «плюс на минус всегда дает минус» (при умножении). Таким образом, ученик решит задачу правильно, и у него не возникнет проблем в будущем, особенно если он планирует пойти в технический университет.
Таким образом, ученик решит задачу правильно, и у него не возникнет проблем в будущем, особенно если он планирует пойти в технический университет.
Вы узнали, что такое алгебра. Желаем вам успешного познания этого сложного раздела математики.
Разница между алгеброй и арифметикой
Ключевое отличие: арифметика и алгебра — это две ветви математики. Арифметика, являясь самой основной из всех областей математики, имеет дело с базовым вычислением чисел, используя такие операции, как сложение, умножение, деление и вычитание. С другой стороны, алгебра использует числа и переменные для решения задач. Он основан на применении обобщенных правил для решения проблем.
Арифметика и алгебра — это две разные ветви математики. Арифметика, сам термин был получен из греческого слова, означающего число. Это самая основная отрасль математики. Это все о числах, и поэтому обычно используется всеми в повседневной жизни. Элементарная арифметика работает вокруг четырех основных операций: сложение, вычитание, деление и умножение. Он просто использует числа для различных типов расчетов
Он просто использует числа для различных типов расчетов
Высшая арифметика также известна как теория чисел. Это касается характеристик целых чисел, рациональных чисел, иррациональных чисел и действительных чисел.
С другой стороны, алгебра является еще одним разделом математики. Слово происходит от арабского слова al-jabr, которое является древним медицинским термином, означающим «воссоединение сломанных частей». Это можно рассматривать как следующий уровень математики после основания арифметики. В отличие от арифметики, он имеет дело с неизвестными величинами в сочетании с числами. Можно легко идентифицировать алгебраическую операцию с символами X, Y, a, b и т. Д. Она в основном касается правил для манипулирования арифметической операцией.
Он включает в себя полномочия, алгоритм и комплексные числа также. Алгебра использует произведения и факторинг, квадратичные формальные и биномиальные теоремы и т. Д., Чтобы найти решение. Основные алгебраические свойства используются для оценки алгебраических уравнений.
Например, 3 + 7 = 7 + 3, это арифметическое выражение
Принимая во внимание, что a + b = b + a является алгебраическим уравнением, потому что оно будет справедливо для ряда ситуаций. Арифметика может показывать некоторую регулярность, тогда как алгебра дает выражение для определения этих закономерностей на основе закономерностей. Таким образом, арифметику можно рассматривать как вычисление определенных чисел, тогда как алгебра — это обобщение некоторых условий, которые будут выполняться для всех чисел, или целых чисел, или целых чисел и т. Д.
В отличие от элементарной арифметики, элементарная алгебра использует букву для решения з
Разница между алгеброй и арифметикой
Алгебра и арифметика
В чем разница между алгеброй и арифметикой? Арифметика и алгебра — две разные области математики, поэтому важно, чтобы мы могли различать, из чего состоит каждая из них.
В чем разница между алгеброй и арифметикой
Арифметика
Сам термин «арифметика» происходит от греческого слова, означающего число.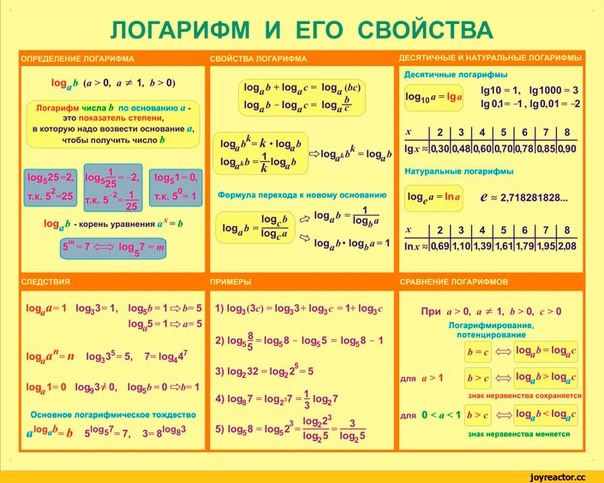 Это самый основной раздел математики, охватывающий все, что имеет отношение к числам, поэтому люди используют его в повседневной жизни.Традиционная арифметика работает с четырьмя основными операциями, а именно: сложение, вычитание, умножение и деление. Он просто выполняет различные типы вычислений с использованием чисел.
Это самый основной раздел математики, охватывающий все, что имеет отношение к числам, поэтому люди используют его в повседневной жизни.Традиционная арифметика работает с четырьмя основными операциями, а именно: сложение, вычитание, умножение и деление. Он просто выполняет различные типы вычислений с использованием чисел.
Верхняя арифметика также известна как теория чисел. Это связано с характеристиками целых чисел, рациональных чисел, иррациональных чисел и действительных чисел.
Алгебра
С другой стороны, алгебра — это еще один раздел математики. Слово происходит от арабского (именно арабы внесли наибольший вклад в эту ветвь) аль-Джабр, старого медицинского термина, значение которого можно назвать «воссоединение осколков».Алгебру можно рассматривать как второй уровень математики после арифметики. В отличие от первого, он работает с неизвестными значениями, которые комбинируются с числами.
Алгебраические операции можно легко идентифицировать по таким символам, как X, Y, A, B… Обычно это основные переменные для работы с алгебраическими операциями. Алгебра связана с правилами, которым следуют, чтобы управлять арифметическими операциями или работать с ними.
Алгебра связана с правилами, которым следуют, чтобы управлять арифметическими операциями или работать с ними.
Кроме того, он включает сложные алгоритмы и числа.Он использует произведения и факторизацию, формальные теоремы и квадратные биномы; среди прочего, чтобы решить уравнения.
Например:
3 + 3 = 6 (это арифметическое выражение)
x = 3 (это алгебраическое выражение).
Короче говоря, мы можем сказать, что арифметика — это вычисление определенных чисел, а алгебра — это обобщение некоторых условий, которые истинны для всех целых чисел. В отличие от элементарной арифметики, элементарная алгебра использует буквы в качестве переменных для решения задач; однако высшая арифметика использует буквы так же, как и в остальных разделах математики.Ключевое различие между арифметикой и алгеброй:
Арифметика, будучи самым основным разделом математики, занимается основным анализом чисел; за счет использования таких операций, как сложение, вычитание, умножение и деление. В то время как алгебра становится вторым уровнем среди разделов математики и использует как числа, так и переменные для решения задач. Он основан на широко распространенном применении для решения проблем.
В то время как алгебра становится вторым уровнем среди разделов математики и использует как числа, так и переменные для решения задач. Он основан на широко распространенном применении для решения проблем.
Бесплатный онлайн-курс алгебры | Справка по алгебре
Дом
11.Алгебраические выражения
Четыре операции и их признаки.
Функция круглых скобок.
Термины в сравнении с коэффициентами .
Полномочия и экспоненты.
Порядок работы.
Вычисление алгебраических выражений.
12. Числа со знаком: положительные и отрицательные
Целые числа.
Алгебраический знак и модуль.
Вычитание большего числа из меньшего.
Номер строки.
Отрицательное значение любого числа.
13. Сложение и вычитание чисел со знаком
«Добавление» отрицательного числа.
Условия наименования. Правило добавления терминов.
Вычитание отрицательного числа.
14. Умножение и деление чисел со знаком
Правило знаков.
15. Некоторые правила алгебры
Правило симметрии. Коммутативные правила. Перевернутые.
Два правила для уравнений.
16. Взаимные и ноль
Определение обратных величин.Определение деления. Правила для 0.
17. Удаление символов группировки
Круглые скобки. Кронштейны. Подтяжки.
Отношение b — a до a — b .
18. Добавление похожих терминов
19. Линейные уравнения
Закон обратного.
Транспонирование.
Логическая последовательность операторов.
Простые дробные уравнения.
10. Проблемы со словами
11. Неравенство
12.Абсолютное значение
Уравнения абсолютных значений.
Неравенства по абсолютной величине.
13. Экспоненты
Полномочия числа.
Правила экспонент: когда складывать, когда умножать.
14. Умножение: правило распределения
15. Общий множитель
Определение полинома от x .
Факторинговые полиномы.
Факторинг по группировке.
Уравнения, в которых неизвестное является общим фактором.
16. Умножение биномов
Квадратичные трехчлены.
17. Факторинговые трехчлены
Квадраты в разных аргументах.
18. Квадрат двучлена
Трехчлены полного квадрата.
Квадрат трехчлена.
Завершение кв.
Геометрическая алгебра.
19. Разница двух квадратов
Краткое изложение умножения / факторинга.
Факторинг по группировке.
Сумма и разность любых двух степеней: a n ± b n .
20. Экспоненты II
Отрицательные показатели. Экспонента 0. Научное обозначение.
21. Алгебраические дроби
Рациональные выражения. Принцип эквивалентных дробей. Сведение к самым низким срокам.
Сведение к самым низким срокам.
22. Умножение и деление алгебраических дробей
Сложные фракции.
23. Сложение алгебраических дробей
Наименьшее общее кратное (НОК) ряда терминов.
24. Уравнения с дробями
Очистка фракций.
25. Проблемы со словами, приводящие к уравнениям с дробями
Целое равно сумме частей.
То же время Проблема: восходящий-нисходящий.
Полная проблема времени. Проблема с работой.
26. Радикалы: рациональные и иррациональные числа
Квадратные корни.
Уравнения x ² = a и главный квадратный корень.
Рационализация знаменателя.
Реальные числа.
27. Упрощающие радикалы
Дробное подкоренное выражение.
28. Умножающие и делящие радикалы
Сопряженные пары.
29. Рациональные показатели
Корни чисел. Индекс радикала.
Дробные показатели.
Отрицательные показатели.
30. Сложные или воображаемые числа
Квадратный корень отрицательного числа.
Реальная и мнимая составляющие.
Сопряженные пары.
31. Прямоугольные координаты
Прямые.
32. Формула расстояния Пифагора
Расстояние точки от начала координат.
Расстояние между любыми двумя точками.
Доказательство теоремы Пифагора.
33. Уравнение и график прямой
Уравнение первой степени и его график.
Вертикальные и горизонтальные линии.
34. Уклон прямой
Форма пересечения наклона уравнения прямой.
Общий вид.
Параллельные и перпендикулярные линии.
Формула «точка-наклон». Двухточечная формула.
35. Одновременные линейные уравнения
Метод сложения. Метод подстановки. Правило Крамера: метод определителей.
Три уравнения с тремя неизвестными.
36. Проблемы со словами, которые приводят к системным уравнениям
Инвестиционные проблемы. Проблемы со смесью.
Проблемы со смесью.
Проблемы вверх-вниз по течению.
37. Квадратные уравнения
корни квадратичного.
Решение по факторингу.
Завершение кв.
Квадратичная формула.
Дискриминант.
График квадратичной: парабола.
38. Логарифмы
Определение. Три закона логарифмов.
Десятичный логарифм.
39. Вариант
Прямое изменение. Константа пропорциональности.
Зависит от площади. Меняется обратно пропорционально. Зависит от обратного квадрата.
Авторские права © 2020 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Математика булевой алгебры (Стэнфордская энциклопедия философии)
Булева алгебра (BA) — это множество \ (A \) вместе с двоичными
операции + и \ (\ cdot \) и унарная операция \ (- \), а также элементы
0, 1 из \ (A \) такие, что выполняются следующие законы: коммутативность и
ассоциативные законы сложения и умножения, законы распределения
как для умножения над сложением, так и для сложения над
умножение и следующие специальные законы:
\ [\ begin {align *}
(х + (х \ cdot у) & = х \\
(х \ cdot (х + у) & = х \\
х + (-х) & = 1 \\
х \ cdot (-x) & = 0
\ конец {выравнивание *} \]
Эти законы лучше понять на базовом примере
BA, состоящий из набора \ (A \) подмножеств множества \ (X \) замкнутых
при операциях объединения, пересечения, дополнения с
относительно \ (X \), с членами \ (\ varnothing \) и \ (X \). Можно
Можно
легко вывести из этих аксиом многие элементарные законы, имея в виду
этот пример для мотивации. Любая БА имеет естественный частичный порядок
\ (\ le \) определил на нем, сказав, что \ (x \ le y \) тогда и только тогда, когда \ (x
+ у = у \). В нашем основном примере это соответствует \ (\ substeq \). Из
Особое значение имеет двухэлементная БА, образованная набором
\ (X \), чтобы иметь только один элемент. Двухэлементная БА показывает прямую
связь с элементарной логикой. Два члена, 0 и 1, соответствуют
к лжи и правде соответственно.Затем логические операции выражают
обычные таблицы истинности для дизъюнкции (с \ (+) \), конъюнкции
(с \ (\ cdot) \) и отрицанием (с \ (-) \). Важный элементарный
В результате уравнение выполняется во всех БА тогда и только тогда, когда оно выполняется в
двухэлементный БА. Затем мы определяем \ (x \ oplus y = (x \ cdot -y) + (y
\ cdot -x) \). Тогда \ (A \) вместе с \ (\ oplus \) и \ (\ cdot \), вдоль
с 0 и 1, образует кольцо с единицей, в котором каждый элемент
идемпотентный. Наоборот, для такого кольца с добавлением \ (\ oplus \)
Наоборот, для такого кольца с добавлением \ (\ oplus \)
и умножение, определите \ (x + y = x \ oplus y \ oplus (x \ cdot y) \)
и \ (- x = 1 \ oplus x \).Это превращает кольцо в BA. Эти двое
процессы противоположны друг другу и показывают, что теория
Булевых алгебр и колец с единицей, в которых каждый элемент
идемпотенты по определению эквивалентны. Это ставит теорию БА
в стандартный объект исследования в алгебре. Атом в БА — это
ненулевой элемент \ (a \) такой, что не существует элемента \ (b \) с \ (0 \ lt
б \ л а \). БА является атомарной, если каждый ненулевой элемент БА выше
атом. Конечные БА атомарны, как и многие бесконечные БА.Под
частичный порядок \ (\ le \) выше, \ (x + y \) является точной верхней границей
\ (x \) и \ (y \), а \ (x \ cdot y \) — точная нижняя граница
\ (х \) и \ (у \). Мы можем обобщить это: \ (\ Sigma X \) — наименьшее
верхняя граница множества \ (X \) элементов, а \ (\ Pi X \) — наибольшее
нижняя граница множества \ (X \) элементов. Это не для всех
множества во всех булевых алгебрах; если они существуют всегда, логическое
алгебра называется полной.
Некоторые алгебраические конструкции имеют очевидные определения и простые
свойства для БА: подалгебры, гомоморфизмы, изоморфизмы и
прямые произведения (даже бесконечного числа алгебр).Некоторые другие
Стандартные алгебраические конструкции более характерны для БА. Идеал в
BA — это подмножество \ (I \), замкнутое относительно +, с 0 в качестве члена, и такое
что если \ (a \ le b \ in I \), то также \ (a \ in I \). Хотя нет
сразу очевидно, это то же самое, что и теоретико-кольцевой
концепция. Существует двойственное понятие фильтра (не имеющее аналога в
кольца в целом). Фильтр — это подмножество \ (F \), замкнутое относительно \ (\ cdot \),
имеющий 1 в качестве члена и такой, что если \ (a \ ge b \ in F \), то также
\ (а \ в F \). Ультрафильтр на \ (A \) — это фильтр \ (F \) с
следующие свойства: \ (0 \ not \ in F \), и для любого \ (a \ in A \) либо
\ (а \ в F \) или \ (- а \ в F \).Для любого \ (a \ in A \) пусть
\ [
S (a) = \ {F: F \ text {является ультрафильтром на} A \ text {и} a \ in F \}.
\]
Тогда \ (S \) — изоморфизм на БА подмножеств множества \ (X \)
все ультрафильтры на \ (A \). Это устанавливает основной камень
теорема о представлении и проясняет происхождение БА как конкретных
алгебры множеств. Более того, множества \ (S (a) \) можно объявить
база топологии на \ (X \), что превращает \ (X \) в полностью
несвязное компактное хаусдорфово пространство. Это устанавливает один-один
соответствие между классом БА и классом таких
пробелы.Как следствие, очень часто используемые в теории БА, многие
топологические теоремы и концепции имеют последствия для БА. Если \ (x \)
является элементом БА, пусть \ (0x = -x \) и \ (1x = x \). Если
\ ((x \) (0), \ (\ ldots x (m — 1)) \) — конечная последовательность элементов
BA \ (A \), то каждый элемент подалгебры в \ (A \), порожденный
\ (\ {x (0), \ ldots, x (m — 1) \} \) можно записать как сумму мономов
\ (e (0) x (0) \ cdot \ ldots \ cdot e (m — 1) x (m — 1) \) для \ (e \) в некотором наборе
функций, отображающих \ (m = \ {0, \ ldots, m — 1 \} \) в \ (2 = \ {0,
1 \} \). Это алгебраическое выражение дизъюнктивной нормальной формы
Это алгебраическое выражение дизъюнктивной нормальной формы
Теорема сентенциальной логики. Функция \ (f \) из множества \ (X \)
образующие БА \ (А \) в БА \ (B \) продолжаются до
гомоморфизм тогда и только тогда, когда
\ [
е (0) х (0) \ cdot \ ldots \ cdot e (m — 1) x (m — 1) = 0
\]
всегда означает, что
\ [e (0) f (x (0)) \ cdot \ ldots \ cdot e (m — 1) f (x (m — 1)) = 0.
\]
Это критерий расширения Сикорского. Каждый BA \ (A \) может быть
вложено в полный BA \ (B \) таким образом, что каждый элемент
\ (B \) — наименьшая верхняя граница набора элементов \ (A \).\ (B \) есть
единственна с точностью до \ (A \) — изоморфизма и называется пополнением
\ (А \). Если \ (f \) — гомоморфизм БА \ (А \) в полную БА
\ (B \), и если \ (A \) — подалгебра в \ (C \), то \ (f \) может быть
продолжается до гомоморфизма \ (C \) в \ (B \). Это
Теорема Сикорского о продолжении. Еще одно общее алгебраическое понятие
применимым к булевым алгебрам является понятие свободного
алгебра. Это может быть конкретно сконструировано для БА. А именно бесплатные
А именно бесплатные
BA на \ (\ kappa \) — это БА замкнутых открытых подмножеств двух элементов
дискретное пространство возведено в степень \ (\ kappa \).
Есть много важных специальных классов булевой алгебры.
как для внутренней теории БА, так и для
заявок:
- Атомные БА, уже упомянутые выше.
- безатомных БА, которые определены как
БА без атомов. Например, любое бесконечное
свободный БА безатомен. - Полные BA, определенные выше. Это специально
важен в основах теории множеств. - Интервальные алгебры. Они получены из линейно упорядоченных множеств
\ ((L, \ lt) \) с первым элементом следующим образом.Один берет самое маленькое
алгебра подмножеств \ (L \), содержащая все полуоткрытые
интервалы [\ (a, b) \) с \ (a \) в \ (L \) и
\ (b \) в \ (L \) или равно \ (\ infty \). Эти БА полезны в
изучение алгебр Линденбаума-Тарского. Каждый счетный БА
изоморфна интервальной алгебре, а значит, счетная БА может быть
описывается указанием упорядоченного набора, который изоморфен
соответствующая интервальная алгебра.
- Древовидные алгебры. Дерево — это частично упорядоченное множество \ ((T, \ lt) \) в
которой упорядочен набор предшественников любого элемента.Дано
такое дерево, рассматривается алгебра подмножеств \ (T \), порожденная
всеми множествами вида \ (\ {b: a \ le b \} \) для некоторого \ (a \) в
\ (Т \). - Суператомные БА. Это БА
которые не только атомарны, но таковы, что каждая подалгебра и
гомоморфный образ атомарен.
Многое из более глубокой теории булевых алгебр, рассказывая об их
структуру и классификацию, можно сформулировать в терминах определенных
функции, определенные для всех булевых алгебр с бесконечными кардиналами
как ценности.Мы определяем некоторые из наиболее важных из этих кардинальных
функций, и указать некоторые из известных структурных фактов, в основном
сформулировано на их основе
- Клеточность \ (c (A) \) БА есть супремум
мощности множеств попарно непересекающихся элементов \ (A \). - Подмножество \ (X \) БА \ (A \) независимо, если
\ (X \) — это набор свободных образующих подалгебры,
генерирует. Независимость \ (A \) есть супремум
Независимость \ (A \) есть супремум
мощности независимых подмножеств \ (A \). - Подмножество \ (X \) БА \ (A \) плотно в \ (A \), если
каждый ненулевой элемент \ (A \) является \ (\ ge \) ненулевым элементом
\(ИКС\). \ (\ Pi \) — вес \ (A \) — это наименьшая мощность
плотного подмножества \ (A \). - Два элемента \ (x, y \) из \ (A \) несравнимы
если ни один не является \ (\ le \) другим. Супремум мощностей
подмножество \ (X \) в \ (A \), состоящее из попарно несравнимых
элементов — это несравнимость \ (A \). - Подмножество \ (X \) из \ (A \) неизбыточно, если ни один элемент
\ (X \) находится в подалгебре, порожденной другими.
Важным фактом, касающимся клеточности, является метод Эрдеша-Тарского.
Теорема: если клеточность БА — особый кардинал, то существует
фактически представляет собой набор непересекающихся элементов такого размера; на клеточность
штатный лимит (недоступен), есть контрпримеры. Каждые
бесконечная полная БА имеет независимое подмножество того же размера, что и
алгебра. Каждый бесконечный BA \ (A \) имеет неизбыточную несравнимую
Каждый бесконечный BA \ (A \) имеет неизбыточную несравнимую
подмножество, размер которого равен \ (\ pi \) — весу \ (A \). Каждый интервал
алгебра имеет счетную независимость.Суператомная алгебра не
даже иметь бесконечное независимое подмножество. Любая древовидная алгебра может быть
вложено в интервальную алгебру. БА только с удостоверением личности
автоморфизм называется жестким. Существуют жесткие полные БА, а также
жесткие интервальные алгебры и жесткие древовидные алгебры.
Совсем недавно многие кардинальные функции типа min-max были
учился. Например, малая независимость — это наименьший размер
бесконечное максимальное независимое множество; и малая клеточность — это
наименьший размер бесконечного разбиения единицы.
Основной результат Тарского состоит в том, что элементарная теория булевых
алгебры разрешимы. Даже теория булевых алгебр с
выделенный идеал разрешим. С другой стороны, теория
Булева алгебра с выделенной подалгеброй неразрешима. И то и другое
результаты разрешимости и неразрешимости распространяются на различные
пути к булевым алгебрам в расширениях логики первого порядка.
Очень важная конструкция, которая переносится на многие логики и
многих алгебр, кроме булевых, является построением
Булева алгебра связана с предложениями в некоторой логике.В
Самый простой случай — это логика предложений. Здесь есть символы предложений,
и общие связки, составляющие из них более длинные предложения:
дизъюнкция, союз и отрицание. Дан набор \ (A \) предложений
в этом языке два предложения \ (s \) и \ (t \) эквивалентны по модулю
\ (A \) тогда и только тогда, когда двусмысленность между ними является логическим
следствие \ (A \). Классы эквивалентности могут быть преобразованы в БА.
такой, что + соответствует дизъюнкции, \ (\ cdot \) — конъюнкции и
\ (- \) к отрицанию. Любая БА изоморфна одной из этих форм.Можно
сделайте что-нибудь подобное для теории первого порядка. Пусть \ (T \) —
теория первого порядка в языке первого порядка \ (L \). Мы называем формулы
\ (\ phi \) и \ (\ psi \) эквивалент при условии, что \ (T \ vdash \ phi
\ leftrightarrow \ psi \). Класс эквивалентности предложения \ (\ phi \)
обозначается [\ (\ phi \)]. Пусть \ (A \) — совокупность всех
Пусть \ (A \) — совокупность всех
классы эквивалентности по этому отношению эквивалентности. Мы можем сделать \ (A \)
в БА следующими определениями, которые легко
обосновано:
\ [\ begin {align *}
[\ phi] + [\ psi] & = [\ phi \ vee \ psi] \\
[\ phi] \ cdot [\ psi] & = [\ phi \ wedge \ psi] \\
— [\ phi] & = [\ neg \ phi] \\
0 & = [\ mathrm {F}] \\
1 & = [\ mathrm {T}]
\ конец {выравнивание *} \]
Каждая БА изоморфна БА Линденбаума-Тарского.
алгебра.Однако одно из самых важных применений этих классических
Алгебры Линденбаума-Тарского должны описать их для важных теорий.
(обычно разрешимые теории). Для счетных языков это может быть
делается путем описания их изоморфных интервальных алгебр. Обычно это
дает доскональное знание теории. Вот несколько примеров:
| Теория | Изоморфна интервальной алгебре на | |
| (1) | по существу неразрешимая теория | \ (\ mathbb {Q} \), рациональные числа |
| (2) | БА | \ (\ mathbb {N} \ times \ mathbb {N} \), квадрат натуральных чисел, упорядоченный лексикографически |
| (3) | линейных заказа | \ (\ mathbf {A} \ times \ mathbb {Q} \) упорядочены антилексикографически, где \ (\ mathbf {A} \) равно \ (\ mathbb {N} ^ \ mathbb {N} \) в обычном порядке |
| (4) | абелевых группы | \ ((\ mathbb {Q} + \ mathbf {A}) \ times \ mathbb {Q} \) |
В теории моделей можно принимать значения в любом полном БА, а не в
двухэлементный БА. Эта теория булевых моделей была развита
Эта теория булевых моделей была развита
примерно в 1950–1970 годах, но с тех пор почти не работал. Но
частный случай, булевозначные модели для теории множеств, очень
на переднем крае современных исследований теории множеств. Это фактически формирует
эквивалентный способ взглянуть на форсирующую конструкцию Коэна, и
имеет ряд технических преимуществ и недостатков. Философски это
кажется более удовлетворительным, чем концепция принуждения. Мы описываем это
случай теории множеств здесь; тогда станет очевидно, почему только завершать
Рассмотрены БА.Пусть B — полная БА. Сначала мы определяем
Булевозначный универсум \ (V (B) \). Обычный
теоретико-множественный универсум можно отождествить с \ (V \) (2), где 2
— двухэлементная БА. Определение дается трансфинитной рекурсией, где
\ (\ alpha, \ beta \) — порядковые числа, а \ (\ lambda \) — предельный порядковый номер:
\ [\ begin {align *}
V (B, 0) & = \ varnothing \\
V (B, \ alpha + 1) & = \ {f: \ dom (f) \ subset V (B, \ alpha)
\ text {and} \ range (f) \ subset B \} \\
V (B, \ lambda) & = \ bigcup _ {\ beta \ lt \ lambda} V (B, \ beta). \ конец {выравнивание *} \]
\ конец {выравнивание *} \]
где \ (\ dom (f) \) — область определения функции \ (f \), а \ (\ range (f) \) —
диапазон функции \ (f \). \ (B \) -значная вселенная является собственно
класс \ (V (B) \), который является объединением всех этих \ (V \) s. Следующий
определяется довольно сложной трансфинитной рекурсией над
обоснованно устанавливает значение теоретико-множественной формулы с элементами
булевозначной вселенной, присвоенной его свободным переменным:
\ [\ begin {align *}
\ val {x \ in y} & = \ sum_ {t \ in \ dom (y)} \ val {x = t} \ cdot y (t) \\
\ val {x \ substeq y} & = \ prod_ {t \ in \ dom (x)} -x (t) + \ val {t \ in y} \\
\ val {x = y} & = \ val {x \ substeq y} \ cdot \ val {y \ substeq x} \\
\ val {\ neg \ phi} & = — \ val {\ phi} \\
\ val {\ phi \ vee \ psi} & = \ val {\ phi} + \ val {\ psi} \\
\ val {\ exists x \ phi (x)} & = \ sum_ {a \ in V (B)} \ val {\ phi (a)}.\ конец {выравнивание *} \]
Функции — Алгебра — Математика A-Level Revision
В этом разделе рассматриваются функции в рамках более широкой темы алгебры.
Функцию можно рассматривать как правило, которое берет каждый элемент x набора и присваивает ему одно и то же значение y , известное на его изображении.
x → Функция → y
Буква, например f, g или h , часто используется для обозначения функции. Функция, которая возводит число в квадрат и складывает 3, может быть записана как f (x) = x 2 + 5 .Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Пример
f (4) = 4 2 + 5 = 21, f (-10) = (-10) 2 +5 = 105 или, альтернативно, f : x → x 2 + 5 .
Фраза «y является функцией x» означает, что значение y зависит от значения x, поэтому:
- y можно записать через x (например, y = 3x).
- Если f (x) = 3x и y является функцией x (т.
 е. y = f (x)), тогда значение y, когда x равно 4, равно f (4), которое находится путем замены x «s на 4» s.
е. y = f (x)), тогда значение y, когда x равно 4, равно f (4), которое находится путем замены x «s на 4» s.
Пример
Если f (x) = 3x + 4, найти f (5) и f (x + 1).
f (5) = 3 (5) + 4 = 19
f (x + 1) = 3 (x + 1) + 4 = 3x + 7
Домен и диапазон
Область функции — это набор значений, которые вам разрешено вводить в функцию (то есть все значения, которые может принимать x).Диапазон функции — это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x). Итак, если y = x 2 , мы можем выбрать в качестве домена все действительные числа. Диапазон — это все действительные числа, большие (или равные) нулю, поскольку если y = x 2 , y не может быть отрицательным.
Один к одному
Мы говорим, что функция — это взаимно однозначно , если для каждой точки y в диапазоне функции существует только одно значение x такое, что y = f (x). f (x) = x 2 не один к одному, потому что, например, есть два значения x, такие что f (x) = 4 (а именно –2 и 2). На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.
f (x) = x 2 не один к одному, потому что, например, есть два значения x, такие что f (x) = 4 (а именно –2 и 2). На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.
Составные функции
fg означает выполнение функции g, затем функции f. Иногда fg записывается как fog
.
Пример
Если f (x) = x 2 и g (x) = x — 1, то
gf (x) = g (x 2 ) = x 2 — 1
fg (x) = f (x — 1) = (х — 1) 2
Как видите, fg не обязательно равно gf
Обратная функция
Обратной функцией функции является функция, которая обращает эффект исходной функции.Например, y = 2x, обратное y = ½ x.
Чтобы найти обратную функцию, поменяйте местами x «s и y» и сделайте y предметом формулы.
Пример
Найдите обратное к f (x) = 2x + 1
Пусть y = f (x), поэтому y = 2x + 1
поменять местами x «s и y» s:
x = 2y + 1
Сделайте y объектом формулы:
2y = x — 1, поэтому y = ½ (x — 1)
Следовательно, f -1 (x) = ½ (x — 1)
f -1 (x) — это стандартное обозначение, обратное f (x). Обратное считается существующим тогда и только тогда, когда существует функция f -1 с ff -1 (x) = f -1 f (x) = x
Обратное считается существующим тогда и только тогда, когда существует функция f -1 с ff -1 (x) = f -1 f (x) = x
Обратите внимание, что график f -1 будет отражением f в линии y = x.
Это видео объясняет больше об обратной функции
Графики
Функции можно изобразить. Функция непрерывная , если ее график не имеет разрывов. Пример прерывистого графа y = 1 / x, поскольку граф нельзя нарисовать, не отрывая карандаш от бумаги:
Функция периодическая , если ее график повторяется через регулярные интервалы, этот интервал известен как период.
Функция равна даже , если она не меняется при замене x на -x. График такой функции будет симметричным по оси ординат. Даже функции, которые являются полиномами, имеют четные степени (например, y = x²).
Функция нечетная , если знак функции изменяется при замене x на -x. График функции будет иметь симметрию вращения относительно начала координат (например, y = x³).
Функция модуля
Модуль числа — это величина этого числа.Например, модуль -1 (| -1 |) равен 1. Модуль x, | x |, равен x для значений x, которые положительны, и -x для значений x, которые отрицательны. Итак, график y = | x | y = x для всех положительных значений x и y = -x для всех отрицательных значений x:
Преобразование графиков
Если y = f (x), график y = f (x) + c (где c — константа) будет графиком y = f (x), сдвинутым на c единиц вверх (в направлении y- ось).
Если y = f (x), график y = f (x + c) будет графиком y = f (x), сдвинутым на c единиц влево.
Если y = f (x), график y = f (x — c) будет графиком y = f (x), сдвинутым на c единиц вправо.
Если y = f (x), график y = af (x) представляет собой отрезок графика y = f (x), масштабный коэффициент (1 / a), параллельный оси x.


 Независимость \ (A \) есть супремум
Независимость \ (A \) есть супремум е. y = f (x)), тогда значение y, когда x равно 4, равно f (4), которое находится путем замены x «s на 4» s.
е. y = f (x)), тогда значение y, когда x равно 4, равно f (4), которое находится путем замены x «s на 4» s.