Темы линейная алгебра: темы, основы, методы, применение, примеры

Содержание

Тема: Линейная алгебра и аналитическая геометрия

Тест № 1

для студентов заочного факультета

Тема: Линейная алгебра и аналитическая
геометрия.

За каждое правильно выполненное
задание начисляется один балл,
в противном случае – ноль баллов.

I. Выяснить, делит ли точка
M(3,7) отрезок AB
пополам, если:

1. A(1,6), B(5,9) 2.
A(-4,6), B(10,8) 3.
A(8,5), B(-5,9) 4. A(1,5),
B(5,9).

II. Указать, принадлежит
ли точка A(4;5) прямой,
если уравнение этой прямой имеет вид:

5.
6.
7.
8.

III.
Известно, что уравнение прямой на рис.
имеет вид Ax+By+C=0. Тогда:

9. AB>0 10.
AC>0 11. BC

IV.
В треугольнике, вершины которого имеют
координаты A(1,2), B(2,5),C(-3,4)
уравнение высоты (CH) имеет
вид:

12. 2x+3y-3=0 13.
3x-5y-2=0

V.
Даны матрицы A, B
и C размера 4×2,
3×4 и 4×3
соответственно. Ответить, верно ли
указан размер матрицы после умножения:

14. [CxB]=4×3 15.
[CxBxA] =3×4

VI.
Указать, имеет ли система уравнений
решение, если:

16.
17.

VII.
Даны точки A(2,5), B(6,3),
C(-3,7), D(3,1).
Найти скалярное произведение:

18.
=11 19.

=28 20.

=-3 21.

=13

VIII.
Выяснить, образуют ли векторы

базис пространства R³,
если:

22.

23.

IX.
Укажите верные свойства определителя:

24. Если к столбцу определителя прибавить
другой столбец этого определителя,
умноженный на два, то определитель
увеличится в два раза.

25. Если какая-либо строка определителя
равна столбцу этого же, то такой
определитель равен нулю.

X.
Укажите случаи, когда матрица имеет
обратную:

26. Прямоугольная
матрица, на главной диагонали которой
стоят единицы.

27. Квадратная
матрица, определитель которой отличен
от нуля.

Часть II.

За каждое правильно выполненное
задание даётся один балл, в
противном случае баллы не начисляются.

Известно
уравнение прямой
.
Указать прямую, перпендикулярную
данной прямой:

a).

b).
c).
d).

Известно
уравнение прямой
.
Указать прямую, параллельную данной
прямой:

a).

b).

c).

d).

3. Найти
результат умножения матриц

и
:

a).

b).

c).

d).

4. Решить
матричное уравнение AX=B,
если
:

a).

b).

c).

d).

5.
Указать число ,
при котором векторы
=(3,2,-1)
и
=(,-8,4)
параллельны:

a). =4
b). =3
c). =-2
d). =-4

6. Указать
число ,
при котором векторы
=(2,-1,3)
и
=(-5,,2
)
перпендикулярны:

a). =5
b). =-6
c) =7
d). =-5

7.
Закончите утверждение: если из линейно
независимой системы векторов, содержащей
более двух векторов, исключить один
вектор, то эта система будет …

a)
линейно зависимой b)
неопределённой

c) неопределённой d) линейно
независимой

8. Закончите
утверждение: всякие два вектора, лежащие
в плоскости

a) ортогональны b)
коллинеарны

c) линейно зависимы d) компланарны

Часть III.

За каждое правильно выполненное
задание даётся три балла, в
противном случае баллы не начисляются.

Даны
три вершины параллелограмма ABCD:
A(1,3,1), B(2,1,3),
C(3,1,-2). Найти координаты
четвёртой вершины и записать в
ответ сумму его координат.
Найти
длину средней линии трапеции ABCD:
A(-2. 5,-15), B(4.5,-5),
C(7,1), D(5,3).
Найти
матрицу, обратную
и записать в ответ сумму всех её
элементов.
Решить
систему:
и записать в ответ сумму
.
Найти
, при котором векторы
линейно зависимы.

Тест
на экзамене будет состоять из других
задач, но содержит материал, отражённый
в этом образце. Количество задач в
экзаменационном тесте в каждой части
также отличается от приведённых здесь.

Содержние дисциплины «Линейная алгебра» : Кафедра МЭО : АлтГТУ

Кафедра «Международные экономические отношения»

Тема 1. Линейная алгебра

Понятие матрицы, типы матриц. Операции над матрицами. Определители квадратных матриц. Минор и алгебраическое дополнение. Способы вычисления определителей, их основные свойства. Формулы Крамера. Обратная матрица. Теорема существования единственной обратной матрицы. Решение систем матричным способом. Ранг матрицы и его вычисление. Общая теория линейных систем. Теорема Кронекера-Капелли. Метод Гаусса для решения определенных систем. Однородные системы и условия ненулевого решения.

Тема 2. Векторная алгебра

Линейные операции над векторами. Проекция вектора на ось, ее свойства. Линейная зависимость векторов. Базис. Декартова система координат. Направляющие косинусы вектора. Скалярное произведение векторов. Свойства. Скалярное произведение в координатной форме, приложения. Векторное и смешанное произведения векторов. Свойства. Векторное и смешанное произведения в координатной форме, приложения. Линейные и аффинные пространства. Размерность. Система координат аффинного пространства. Линейные преобразования (операторы). Собственные векторы и собственные значения о матрице линейного оператора в базисе из собственных векторов. Применение линейных операторов в экономико-математических моделях.

Тема 3. Аналитическая геометрия

Понятия уравнений линии и поверхности. Основные задачи аналитической геометрии. Плоскость. Прямая в пространстве. Прямая на плоскости. Полярная система координат. Кривые второго порядка. Классификация уравнений второй степени. Пример приведения квадратичной формы к каноническому виду. Плоскости в аффинном пространстве; параметрическое задание плоскости. Геометрическое истолкование множества решений неоднородной системы линейных уравнений. Выпуклые множества.

Тема 4. Элементы линейного программирования

Построение опорных планов задачи линейного программирования. Решение задачи линейного программирования графическим методом. Решение невырожденной задачи линейного программирования симплекс-методом.

Литература и учебно-методические материалы

Основная литература

Высшая математика для экономистов: Учеб. Пос. для вузов/Н.Ш. Кремер и др. Под ред. Н.Ш. Кремера.-М.:Банки и биржи,БНИТИ,1997.
Шипачев В.С. Высшая математика: учебник для студентов нематематических специальностей вузов/ Под ред. А.Н. Тихоноваю- М.Высшая школа, 1985.- 368 с.
Красс М.С. Математика для экономических специальностей.- М.: ИНФРА-М 1999.-463 с.
Карасев А.И., Аксютина З. М., Савельева Т.И. Курс высшей математики для экономических вузов. Ч 1−2.- М.: Высшая школа, 1982 г.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.- М.: Высшая школа, 1986.- Ч.1−2.- 319 с., 365 с.
Рябушко А.П. и др. Сборник индивидуальных заданий по высшей математике.- Минск: Высшая школа, 1989,- Ч.1−3.
Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. Академия народного хоз-ва при правительстве РФ. Издательство “Дело”, Москва.2000 г.

Дополнительная литература

Егорова Г.В. Линейная алгебра. Определители и матрицы. Метод. Указания и варианты заданий к типовым расчетам по курсу высшей математики для студентов всех специальностей/ Алт. политехн. Ин-т им. И.И. Ползунова.- Барнаул: Б.И.,19?

Жданова Е.М., Поддубная М.Л., Ким Л.С. Элементы векторной алгебры: Методические указания и варианты заданий для студентов всех специальностей/ Алт. политехн. ин-т им. И.И. Ползунова.- Барнаул: Б.И.,1991.- 20 с.

Егорова Г.В. Функции, пределы, непрерывность.: Варианты заданий для самостоятельной работы студентов по курсу высшей математики / Алт. политехн.ин-т им. И.И. Ползунова.- Барнаул: Б.И.,1989.- 34 с.

Царегородцев А.И., Шапиро М.А. Линейная алгебра. Определители и матрицы. Метод. указания и варианты заданий к типовым расчетам по курсу высшей математики для студентов всех специальностей/ АПИ.- Барнаул,1988.- 32 с.

Царегородцев А.И., Шапиро М.А. Линейная алгебра.Системы линейных уравнений. Метод. указания и варианты заданий к типовым расчетам по курсу высшей математики для студентов всех специальностей/ АПИ.- Барнаул:,1988.- 32 с.

Жданова Е.М., Ким Л.С., Поддубная М.Л. Элементы векторной алгебры. Методические указания и варианты заданий для студентов всех специальностей.–АлтГТУ,Барнаул, 1994.–32 с.

Жеронкина Н.Г., Котова А.В., Сыченко Э.И. Аналитическая геометрия. Варианты заданий для СР студентов по курсу ВМ.- Алт.ГТУ, Барнаул, 1994.- 32 с

преп. каф. ВМиММ Мурзина И.П.

Иллюстративный видеокурс по линейной алгебре: 11 уроков

Видеокурс по линейной алгебре с большим количеством анимаций будет полезен при создании компьютерной графики и решении задач ML.

Эти красочные, прекрасно иллюстрированные видеоуроки в Full HD разрешении, созданные выпускником Стэнфорда Грантом Сандерсоном, будут полезны всем, кто проходил или проходит курс по линейной алгебре, но не до конца ощутил, зачем это все нужно и как работает.

Уроки идут в порядке, предполагающем их последовательный просмотр – каждое следующее видео использует знания и иллюстрации из предыдущих. В этих уроках вы не найдете расчетов примеров из задачников по линейной алгебре и строгого доказательства теорем, однако визуализируете основные концепции линейной алгебры, действия с векторами и матрицами. Все видео имеют английские авторские субтитры, при этом первые пять также содержат их перевод на русский язык.

Задача этого краткого курса из 11 уроков – уложить в голове всю образную сторону вопросов, лежащих в основании линейной алгебры при помощи видео с анимацией. Знания в линейной алгебре важны для понимания многих технических дисциплин: computer science, статистики, анализа данных, физики, экономики и т. д.

Однако студенты, изучившие курс линейной алгебры и механически научившиеся массе операций, таких как матричное умножение, нахождение определителя и собственных чисел, обычно не представляют зачем на практике нужны эти инструменты. Курс поможет прочувствовать линейную алгебру на интуитивно понятном геометрическом уровне. Визуальные образы позволят пропустить через себя основные концепции линейной алгебры. Вычисления же всегда можно доверить компьютеру.

В основе любого курса по линейной алгебре лежит понятие о векторе. В первом уроке описываются три представления вектора: с точки зрения студента-физика, студента-программиста и математика. Поясняются понятие вектора в привязке к системе координат и запись в виде столбца чисел. Вводятся операции сложения векторов и умножения на скаляр: как геометрически, так и численно. Даются примеры использования операций над векторами в анализе данных и программировании компьютерной графики.

Во втором уроке вводится понятие базиса и базисных векторов i и j, а также линейной оболочки как множества линейных комбинаций векторов в двухмерном и трехмерном пространствах. Иллюстрируется представление векторов как точек, в которых расположены концы векторов, исходящих из центра системы координат. Вводятся понятия линейно зависимых и линейно независимых векторов.

В третьем уроке видеокурса по линейной алгебре показывается геометрическая интерпретация линейных преобразований (отображений), являющихся наиболее простыми из всех нетривиальных преобразований. Начало координат остается на своем месте, а параллельные и равноудаленные прямые линии сохраняют эти свойства при преобразовании. Через линейные отображения базисных векторов естественным образом можно ввести понятие матрицы.

В качестве примеров автором находятся матрицы для поворота вектора на 90° против часовой стрелки и наклона вектора. Иллюстрируется также случай, соответствующий линейно зависимым базисным векторам, когда двумерное пространство вырождается в линию.

Итак, умножение матрицы на вектор это фактически линейное преобразование вектора. Но что, если к вектору применяется несколько преобразований? Например, в компьютерной графике один за другим кадры сменяют друг друга, и одно изображение преобразуется в следующее. Такое отображение называют композицией преобразований. Как любое преобразование, оно может быть описано матрицей.

Фактически оно является произведением матриц соответствующих линейных отображений. В уроке иллюстрируется как сама операция умножения матриц, так и представление этой операции через последовательные преобразования базисных векторов. Показывается, почему важен порядок умножения одной матрицы на другую.

В этом видео линейные преобразования на плоскости расширяются до случая объемных отображений. Для этого используются уже три базисных вектора, а матрицы линейных преобразований имеют размерность 3х3. Перемножение таких матриц ничем не отличается от перемножения матриц 2х2.

https://www.youtube.com/watch?v=Ip3X9LOh3dk

В предыдущих уроках вы могли заметить, что одни преобразования в линейной алгебре растягивают пространство, а другие сжимают. Интересно определить число, которое показывает как меняется площадь или объем какой-либо фигуры при таких преобразованиях. В видео демонстрируются линейные преобразования различных фигур и соответствующее изменение их площади.

Параметр этого изменения называют определителем (детерминантом).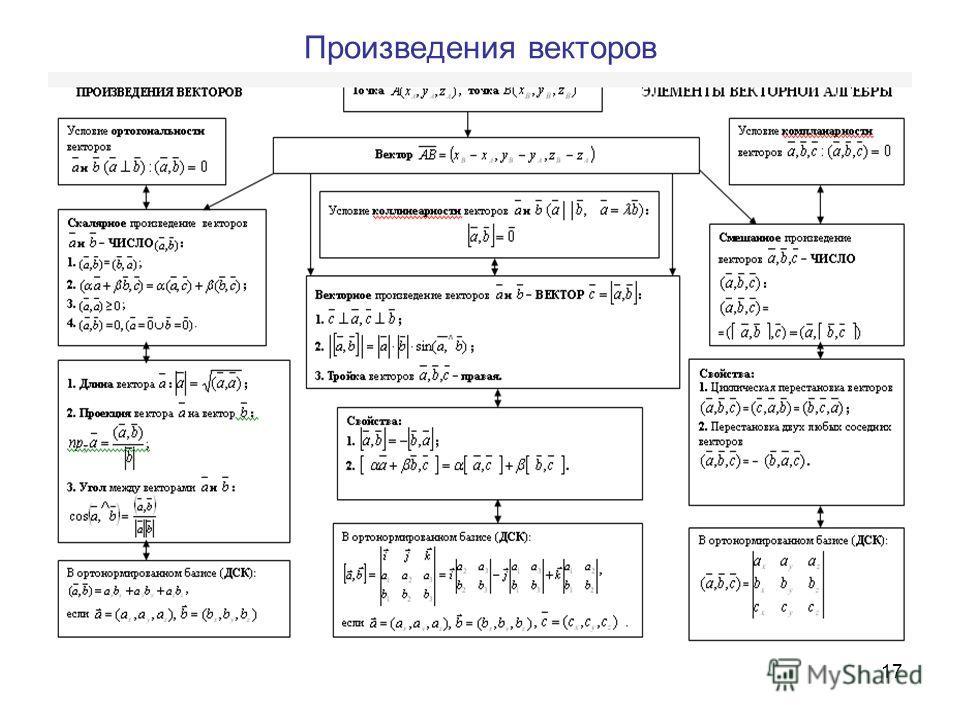 Показывается, почему равенство определителя нулю соответствует уменьшению размерности пространства, а отрицательное значение – изменению ориентации пространства. Из геометрических соображений объясняется формула нахождения определителя.

В начале видео описывается линейная система уравнений и ее представление через матрицу и два вектора в виде Ax = v, в котором мы знаем матрицу A и вектор v. В геометрическом ключе, ища x, мы ищем вектор, который в результате линейного преобразования A совпадет с вектором v.

Такую задачу можно рассмотреть и в обратном ключе: x это тот вектор, в который преобразуется вектор v в результате преобразования, обратного A. Соответствующее отображение обозначают A^-1. Нахождение такой обратной матрицы позволяет решить первое уравнение в виде x = A^-1v.

Урок содержит множество анимаций, иллюстрирующих эту концепцию. Описываются случаи ненулевого и нулевого определителей линейного преобразования. Вводится понятие ранга матрицы – количества измерений пространства, в которое переводит вектор линейное отображение.

Аналогично тому, как в последних видео при помощи квадратных матриц соответствующей размерности было рассмотрено преобразование двумерных векторов в двумерные и трехмерных в трехмерные, возможно и преобразование размерности пространства. В этом видео иллюстрируется как соотносятся размерности таких прямоугольных матриц и пространств, между которыми происходит линейное отображение векторов.

В этом видео дается алгебраическое и геометрическое определения скалярного произведения. Геометрическая интерпретация иллюстрирует тот факт, что знак скалярного произведения указывает на отношение направлений двух векторов. При этом, как подтверждают рассуждения, порядок умножения не влияет на результат скалярного произведения. Показывается, что проекции вектора на различные оси есть ничто иное, как скалярные произведения вектора с базисными векторами этих осей. Объясняется, почему скалярное произведение векторов идентично произведению матрицы-строки на матрицу-столбец.

Геометрический смысл векторного произведения двух векторов – вектор с длиной, равной площади параллелограмма между этими векторами. Направление вектора зависит от ориентации пространства. Соответственно при изменении порядка множителей меняется знак векторного произведения. Таким образом, понятие векторного произведения тесно связано с определением детерминанта.

В начале этого видео для лучшего понимания автор намеренно упрощает картину, усложняя ее по мере рассказа. Показывается как облегчается запись векторного произведения, если воспринимать его как определитель особой матрицы, состоящей из базисных векторов и координат перемножаемых векторов.

Отталкиваясь от последней идеи предыдущего видео и нескольких предшествовавших уроков, автор раскрывает идею векторного произведения трех векторов. Показывается связь между векторным и скалярными произведениями в трехмерном пространстве, а также связь между геометрическим и алгебраическим представлением этих операций.

Стандартно координаты вектора рассматриваются как скалярные числа, описывающие какое количество каждого из базисных векторов нужно взять, чтобы в сумме получить вектор с такими координатами. В этом видеоуроке показано, что при выполнении определенных условий базис может быть выбран различным образом. Базисные вектора лишь задают сетку пространства.

Урок показывает как преобразовать координаты одного базиса к координатам другого при помощи линейных преобразований в виде матриц, состоящих из базисных векторов и обратных матриц для обратного преобразования. В заключительной части на примере поворота на 90° против часовой стрелки иллюстрируется как изменяются в терминах другого базиса линейные преобразования. В результате объясняется, что означает характерное перемножение матриц вида A^-1MA.

Собственные векторы и числа представляют одну из наименее интуитивно понятных тем в линейной алгебре. Однако в геометрическом представлении это просто векторы, которые не отклоняются от своего направления в результате соответствующего им линейного преобразования – векторы растягиваются или сжимаются, но не поворачиваются вокруг начала координат.

В этом и заключается смысл известного выражения Av = λv – линейное преобразование заменяется на число, называемое собственным. Фактически собственные векторы и числа представляют другой способ рассмотрения линейного преобразования.

В уроке также даются определения диагональной и единичной матриц. Показывается логика нахождения собственных чисел и векторов через нулевой определитель. Иллюстрируется, в каких случаях возможны два, один, ноль или бесконечное количество собственных векторов.

В заключении видео описываются особые свойства диагональных матриц и построение нового базиса на собственных векторах. Последняя операция часто применяется в теории машинного обучения для диагонализации матриц. В конце видео дается небольшое упражнение для закрепления материала.

В заключительном видео курса по линейной алгебре автор возвращается к вопросу первого урока – что представляют собой векторы в самом абстрактном смысле?

Функции и линейные операции над функциями можно рассматривать в векторном ключе. Любые операторы, для которых выполняются свойства аддитивности и мультипликативности, можно рассматривать как линейные преобразования. При этом вместо базисных векторов можно использовать базисные функции.

В уроке эта идея иллюстрируется на примере записи полинома, состоящего из любого числа слагаемых, в виде вектора. Показывается как операция взятия производной может быть реализована при помощи матричного оператора, действующего на такой вектор.

Переводя концепции из других областей математического знания (различных векторных пространств) на язык линейной алгебры и составив соответствующие уравнения, рассмотренные в курсе свойства векторов и линейных отображений можно обобщать на другие области знания.

ТЕМА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ И ЛИНЕЙНОЙ АЛГЕБРЫ

Введение в линейную алгебру

Введение в линейную алгебру Матрицы. Определение. Таблица m n чисел вида m m n n mn состоящая из m строк и n столбцов называется матрицей. Элементы матрицы нумеруются аналогично элементам определителя

Подробнее

ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Государственное образовательное учреждение высшего профессионального образования «Московский авиационный институт (национальный исследовательский университет)» Кафедра «Высшая математика» ЛИНЕЙНАЯ АЛГЕБРА

Подробнее

Алгебра и аналитическая геометрия

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Алтайская государственная педагогическая академия»

Подробнее

1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ ЗАНЯТИЕ МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ Дать определение матрицы Классификация матриц по размерам Что такое нулевая и единичная матрицы? При каких условиях матрицы считаются равными?

Подробнее

ЛЕКЦИИ ПО ВЫСШЕЙ АЛГЕБРЕ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» АИ Шерстнёва,

Подробнее

Лекция 28 Глава 1.

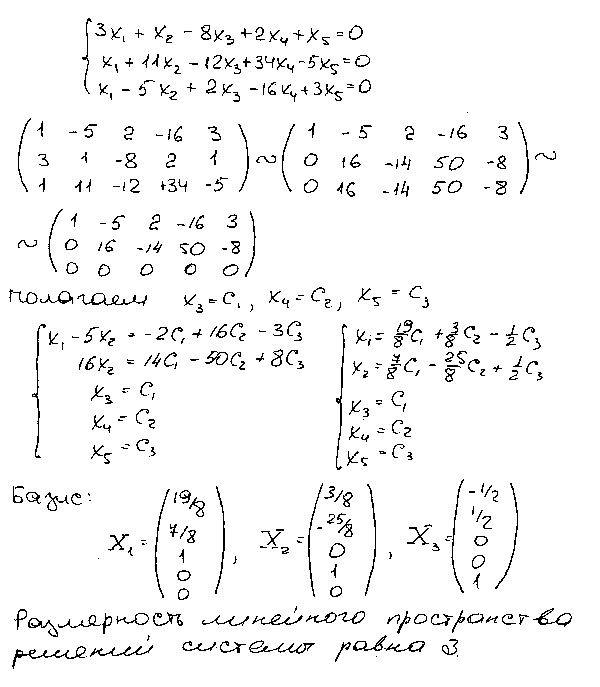Векторная алгебра

Лекция 8 Глава Векторная алгебра Векторы Величины, которые определяются только своим числовым значением, называются скалярными Примерами скалярных величин: длина, площадь, объѐм, температура, работа, масса

Подробнее

РАЗДЕЛ 1. Линейная алгебра.

-й семестр. РАЗДЕЛ. Линейная алгебра. Основные определения. Определение. Матрицей размера mn где m- число строк n- число столбцов называется таблица чисел расположенных в определенном порядке. Эти числа

Подробнее

Лекция 6. Геометрические векторы.

Лектор Гущина Елена Николаевна, кафедра Высшей математики 2. Лекция 6. Геометрические векторы. Вектор как направленный отрезок. Сложение векторов и умножение вектора на число. Свойства линейных операций.

Подробнее

ЛИНЕЙНАЯ АЛГЕБРА ВМЕСТЕ С MAPLE

ЛИНЕЙНАЯ АЛГЕБРА ВМЕСТЕ С MAPLE Усов В.В. 1 Скалярное произведение в арифметическом пространстве 1.1 Определение. Основные свойства Скалярное произведение (X, Y ) векторов X = (x 1, x 2,…, x n ), Y =

Подробнее

Глава 1. Элементы линейной алгебры.

Глава Элементы линейной алгебры Матрицы О п р е д е л е н и е Матрицей размерности m n называется прямоугольная таблица чисел, расставленных в m строк и n столбцов Обозначаются матрицы латинскими буквами,,

Подробнее

1. Требования к знаниям, умениям, навыкам

ПРИЛОЖЕНИЯ Требования к знаниям умениям навыкам Страницы даны по учебнику «Математика в экономике» [] Дополнительные задачи по данному курсу можно найти в учебных пособиях [ 6] Векторы Владеть понятиями:

Подробнее

УДК [ ](075.

8) ISBN ISBN УДК [ ](075.8)

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ КОМПЛЕКСНЫЕ ЧИСЛА Учебное пособие МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение

Подробнее

Тема: Системы линейных уравнений

Линейная алгебра и аналитическая геометрия Тема: Системы линейных уравнений (Метод Гаусса. Системы линейных однородных уравнений) Лектор Рожкова С.В. 0 г. Метод Гаусса (метод исключения неизвестных) Две

Подробнее

Высшая математика для психологов

Саратовский государственный университет им Н Г Чернышевского Галаев СВ, Шевцова ЮВ Высшая математика для психологов Часть (Линейная алгебра и аналитическая геометрия) Саратов 00 СОДЕРЖАНИЕ Глава Векторная

Подробнее

Аналитическая геометрия. Лекция 1.3

Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Аналитическая геометрия Модуль 1. Матричная алгебра. Векторная алгебра Лекция

Подробнее

Глава 4. Матрицы. Лекция Основные понятия.

Лекция 0. Глава 4. Матрицы. В этой главе мы рассмотрим основные виды матриц, операции над ними, понятие ранга матрицы и их приложения к решению систем линейных алгебраических уравнений. 4.. Основные понятия.

Подробнее

Практикум по линейной алгебре

Министерство образования и науки РФ Нижегородский государственный университет им. Н.И. Лобачевского В.К. Вильданов Практикум по линейной алгебре Учебно-методическое пособие Нижний Новгород Издательство

Подробнее

1.

a + b = b + a. 2. (a + b) + c = a + (b + c).

Занятие 5 Линейные операции над векторами 5.1 Сложение векторов. Умножение векторов на числа Закрепленным вектором называется направленный отрезок, определенный двумя точками A и B. Точка A называется

Подробнее

ЛИНЕЙНАЯ АЛГЕБРА. ЧАСТЬ I

Министерство образования и науки Российской Федерации Нижегородский государственный университет им НИ Лобачевского АТ Козинова НН Ошарина ЛИНЕЙНАЯ АЛГЕБРА ЧАСТЬ I Учебное пособие Рекомендовано методической

Подробнее

МАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА

ООО «Резольвента», wwwresolventru, resolvent@listru, (95) 509-8-0 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К Л САМАРОВ МАТЕМАТИКА Учебно-методическое пособие по разделу

Подробнее

ПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.

ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще

Подробнее

Глава 1. Начала линейной алгебры

Глава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные

Подробнее

Геометрические векторы

Геометрические векторы Определение Вектором называется направленный отрезок начальной точкой А и конечной точкой В (который можно перемещать параллельно самому себе) Если начало вектора — точка А, а его

Подробнее

Список литературы на тему: Линейная алгебра

СПИСОК ЛИТЕРАТУРЫ

1. Бубнов, В.А. Линейная алгебра: компьютерный практикум / В.А. Бубнов, Г.С. Толстова, О.Е. Клемешева. — М.: ЛБЗ, 2012. — 168 c.

2. Бурмистрова, Е.Б. Линейная алгебра, дифференциальное исчисление функций одной переменной: Учебник для студ. высш. учеб. заведений / Е.Б. Бурмистрова, С.Г. Лобанов. — М.: ИЦ Академия, 2010. — 336 c.

3. Гомонов, С.А. Математика. Линейная алгебра: Учебно-справочное пособие / С.А. Гомонов. — М.: Форум, НИЦ ИНФРА-М, 2013. — 144 c.

4. Горлач, Б.А. Линейная алгебра: Учебное пособие / Б.А. Горлач. — СПб.: Лань, 2012. — 480 c.

5. Демидович, Б.П. Сборник задач по математике для втузов. В 4-х т.Т. 1. Линейная алгебра и основы математического анализа: Учебное пособие для втузов / Б.П. Демидович. — М.: Альянс, 2011. — 480 c.

6. Епихин, В.Е. Аналитическая геометрия и линейная алгебра. Теория и решение задач: Учебное пособие / В.Е. Епихин, С.С. Граськин. — М.: КноРус, 2013. — 608 c.

7. Ильин, В.А. Линейная алгебра и аналитическая геометрия: Учебник / В.А. Ильин, Г.Д. Ким. — М.: Проспект, 2012. — 400 c.

8. Канатников, А.Н. Линейная алгебра: Учебник для вузов / А.Н. Канатников, А.П. Крищенко; Под ред. В.С. Зарубин. — М.: МГТУ им. Баумана, 2006. — 336 c.

9. Кожухов, И.Б. Сборник задач по математике для втузов. В 4-х т.Т. 1. Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры: Учебное пособие для втузов / И.Б. Кожухов. — М.: Физматлит, 2009. — 288 c.

10. Кочетков, Е.С. Линейная алгебра: Учебное пособие / Е.С. Кочетков, А.В. Осокин. — М.: Форум, 2012. — 416 c.

11. Лунгу, К.Н. Сборник задач по высшей математике. 1 курс: С контрольными работами: линейная алгебра; аналитическая геометрия; основы математического анализа; комплексные числа / К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин, Ю.А. Шевченко. — М.: Айрис-пресс, 2011. — 576 c.

12. Михалев, А.А. Линейная алгебра и аналитическая геометрия: Учебное пособие для студ. учреждений высш. проф. образования / А.А. Михалев, И.Х. Сабитов. — М.: ИЦ Академия, 2013. — 256 c.

13. Просветов, Г.И. Линейная алгебра и аналитическая геометрия: Задачи и решения: Учебно-практическое пособие / Г.И. Просветов. — М.: Альфа-Пресс, 2009. — 208 c.

14. Рудык, Б.М. Линейная алгебра: Учебное пособие / Б.М. Рудык. — М.: НИЦ ИНФРА-М, 2013. — 318 c.

15. Скрыдлова, Е.В. Линейная алгебра: Учебное пособие / Е.В. Скрыдлова, О.О. Белова. — Рн/Д: Феникс, 2012. — 142 c.

16. Шевцов, Г.С. Линейная алгебра: теория и прикладные аспекты: Учебное пособие / Г.С. Шевцов. — М.: Магистр, НИЦ ИНФРА-М, 2013. — 528 c.

Банк тестовых заданий по курсу «Линейная алгебра» Текст научной статьи по специальности «Науки об образовании»

УДК 378.16

Е.Ю. Напеденина, Е.Г. Рудаковская, А.Н. Шайкин Российский химико-технологический университет им. Д.И. Менделеева, Москва, Россия

БАНК ТЕСТОВЫХ ЗАДАНИЙ ПО КУРСУ «ЛИНЕЙНАЯ АЛГЕБРА»

Bank of test items developed for the course «Linear Algebra» and written by twelve educational computer tests on the main sections of this course. In the bank of test items included assignments with the choice of one or more correct answers, job matching, and open the test tasks in which the response tasks calculated numbers to be entered via the keyboard. Computer test program allows you to adjust the number of jobs in a single test, and test time. After testing is complete, a rating, and the system can find answers to the job in which mistakes were made.

Разработан банк тестовых заданий по курсу «Линейная алгебра» и составлено двенадцать обучающих компьютерных тестов по основным разделам этого курса. В банк тестовых заданий включены задания с выбором одного или нескольких правильных ответов, задания на соответствие, а также открытые тестовые задания, в которых ответ расчетных задач вводится числом с помощью клавиатуры. Компьютерная тестирующая программа позволяет регулировать число заданий в одном тесте, а также время тестирования. После завершения тестирования выставляется оценка, и система позволяет просмотреть ответы на задания, в которых были допущены ошибки.

Разработан банк тестовых заданий по курсу «Линейная алгебра», который содержит 202 задания по следующим разделам курса:

1. Уравнения прямой на плоскости.

2. Кривые второго порядка.

3. Векторы. Операции над векторами. Скалярное произведение двух векторов.

4. Векторное произведение двух векторов. Смешанное произведение трех векторов

5. Комплексные числа. Операции над ними.

6. Основная теорема алгебры. Разложение многочлена на множители. Рациональная дробь.

7. Матрицы. Операции над матрицами. Ступенчатый вид, вид Гаусса, ранг матрицы.

8. Определитель матрицы и его свойства. Обратная матрица.

9. Решение систем алгебраических линейных уравнений.

10. Собственные векторы и собственные значения матрицы.

11. Линейные пространства. Базис. Координаты вектора в заданном базисе. Матрица перехода.

12. Евклидовы пространства. Ортогональный и ортонормирован-ный базисы.=1 3 9 2) у = Зх -27

3) Зх + 2у — 6 = 0 4)6х-2у+ 13 = 0

Правильный ответ: 2, 4

Задание 14. Раздел 2. Кривые второго порядка. Укажите уравнение параболы, представленной на рисунке.

Правильный ответ: 2.

Помимо заданий с выбором правильного варианта ответа в банк тестовых заданий включены также расчетные задачи, ответ в которых вводится числом с помощью клавиатуры.

Задание 6. Раздел 4. Векторное произведение двух векторов.

Смешанное произведение трех векторов.

Найдите | а. хЬ|, если \а\ = 5, |Ь| = 10, а ■ Ь = 30.

Правильный ответ: 40

Задание 8. Раздел 9. Решение систем лннейных алгебраических уравнений

Найти значение п, при котором система

х + у + г = 6 < Ъх + у + г = % пх + 2у + 2г = Ы

имеет бесконечно много решений. Ответ вписать целым числом.

Правильный ответ: 4.

Задание 16. Раздел 10. Собственные векторы и собственные значения матрицы_

Найти максимальный порядок присоединенного вектора линейного оператора, заданного матрицей

(6 -2 -1 -Л

3 0 0 -1

10 10 6-2-3 1

Ответ записать целым числом.

Правильный ответ: 2.

В заданиях на соответствие требуется установить соответствие между элементами двух множеств, причем второе множество содержит дис-тракторы — элементы, которым не соответствуют элементы первого множества:

Задание 8. Раздел 5. Комплексные числа. Операции над ними.

Установите соответствие между алгебраической и соответствующей показательной формой записи комплексного числа г:

Алгебраическая форма Показательная форма

(1). -1 + 7 А. 2-е 6

(2). -1 В. 2-е 3

(3). 1 —/л/3 С. 2-е2

(4). 2/ £>. 1-е

ЪЖ: Е. 42-е 4

Правильный ответ: (1)->(£), (2)->(£>), (3)->(Я), (4)->(С). Задание 7. Раздел 6. Основная теорема алгебры. Разложение многочлена на множители, рациональная дробь.

Установите соответствие между правильной рациональной дробью и числом неопределенных коэффициентов при разложении на сумму простейших дробей:

Рациональная дробь Rix) Число неопределенных коэффициентов

(1) + * (х + 7)3 А. 0

(2). Г’ (х-1)2(х2 +4) В. 5

(3). 2 1 + 1 з (х — 2х + 1)х С. 3

<4>- , х» — 4х — 5 В. 2

Е. 4

Е. ‘0 0 -2″

(2) 0 -3 -2 ;(3) 0 0 0 ;(4) 0-14

,0 0 — 2} ,0 0 ,3 1 2,

(5)

В качестве ответа введите последовательно номера выражений без знаков препинания.

Правильный ответ: (4), (1), (3), (5), (2).

На основе разработанных тестовых заданий составлены двенадцать обучающих компьютерных тестов по линейной алгебре, которые размещены на сайте кафедры высшей математики http://kvin.inuctr.ru и используются в учебном процессе.

Работа выполнена по проекту 3.4.1/9387 «Развитие независимой системы оценки качества высшего профессионального образования с использованием тестовых технологий» Аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы (2009-2011 гоДЫ)»

Библиографический список

1. Паркина М. П., Щербаков Д. В. Система компьютерного тестирования для оценки знаний студентов //Повышение ресурсо- и энергоэффективности: наука, технология, образование: тр. Междунар. симпозиума, посвященного 175 — летию со дня рождения Д. И. Менделеева. Т. 1. М.: РХТУ им. Д.И. Менделеева, 2009. С. 80-83.

2. Автоматизация составления тестов для студентов /Г. С. Жукова, Е. Ю. Напеденина, Е. Г. Рудаковская, А. Н. Шайкин //Актуальные проблемы химико-технологического образования». XII Межвуз. учебно-методич. конф.: матер, конф. М.: РХТУ им. Д. И. Менделеева, 2010. С. 94-96.

Вычислительная линейная алгебра

Научная работа: темы и направления для студентов 3 курса МФТИ (2020 год)

Вычислительная линейная алгебра

Научный руководитель Академик РАН, проф., д.ф.-м.н. Тыртышников Е.Е., комната 704, email: This email address is being protected from spambots. You need JavaScript enabled to view it.

1. Разреженные решения в задачах вычислительной линейной алгебры и математической физики.

Часто решение задачи ищется в виде разложения по заданному базису, и заметим, что заведомо существуют базисы, для которых вектор коэффициентов разложения оказывается разреженным. За последние 10-15 лет очень интенсивно развивалось новое научное направление, связанное с поиском разреженных или приближенно разреженных решений, в том числе в задачах линейной алгебры. Здесь сложность заключается прежде всего в том, что неизвестно, какие именно коэффициенты будут ненулевыми. Как выбрать базис, гарантирующий разреженность? Конечно, идеальная ситуация – когда базис содержит искомое решение. Но решение – это как раз то, что мы ищем! Цель исследования – понять, как можно находить разрежающие базисы в задачах математической физики, прежде всего для интегральных уравнений теории потенциала. Есть надежда, что в результате получатся совершенно новые эффективные методы решения многих практически важных задач.

2. Редукция моделей и обучающих выборок в задачах машинного обучения.
Мы постоянно имеем дело с отображениями, действие которых известно только на некоторой части точек их области определения. При этом есть желание понять, как они действуют в других точках. Обычно выбирается некоторая модель отображения с набором параметров, которые определяются с помощью методов машинного обучения. Одна из главных реальных проблем заключается в том, что для обучения необходимо использовать слишком много точек. Есть две идеи о том, как сократить число точек обучения. Во-первых, можно из всего множества точек обучения выбирать наиболее значимые. Во-вторых, можно попытаться редуцировать саму модель, сократив число ее параметров и, как следствие, число обучающих точек. Цель исследования – посмотреть, как эти идеи работают в задачах прогнозирования значений временных рядов по начальному отрезку времени, изучить современные статистические модели и возможности применения тензорных разложений для их эффективной реализации.

3. Как решать операторные уравнения в случае операторов с коэрцитивно расщепляемой главной частью.

Теория сходимости проекционных методов (методов Галеркина) для решения линейного операторного уравнения обычно предполагает выполнение двух условий: (а) аппроксимации для проекторов и (б) коэрцитивности для исходного оператора. Замечательно, что компактное возмущение оператора сохраняет сходимость. Однако есть задачи (например, знаменитое уравнение электрического поля в электродинамике), в которых оператор не является коэрцитивным, но с точностью до компактного возмущения допускает расщепление в прямую сумму коэрцитивных. Выбор составного базиса, объединяющего базисы соответствующих подпространств, дает теоретическое решение вопроса о гарантированно сходящемся методе. Но на практике такой выбор может вести к большим вычислительным трудностям (например, в случае уравнения электрического поля). Цель исследования – в случае несоставного базиса понять, какие его свойства обеспечивают сходимость проекционного метода, и, возможно, разобраться с до сих пор открытым вопросом от том, есть ли такие свойства у базиса Рао-Вилтона-Глиссона, который несколько десятилетий успешно применяется при численном решении уравнения электрического поля.

4. Применение тензорных разложений при решении кинетических уравнений.

Традиционно при решении уравнений Больцмана и уравнений Смолуховского используются стохастические методы, так как классические сеточные методы представляются катастрофически затратными. Совсем недавно для уравнений Больцмана и схожих популяционных уравнений удалось получить эффективные квазисеточные методы, в основе которых лежат традиционные сеточные методы и специальные тензорные представления решения и ядра. Цель исследования – посмотреть, как эти конструкции могут использоваться при решении уравнений Больцмана.

5. Принцип максимального объема в задачах оптимизации.

Принцип максимального объема в задачах малоранговой аппроксимации матриц дает замечательный рецепт для выбора малого числа строк и столбцов – креста, по которому матрица восстанавливается с гарантированной точностью: достаточно выбирать крест, в котором цетральная подматрица будет иметь максимальный объем среди всех подматриц такого же размера. Принцип появился в ИВМ РАН и недавно получил новое развитие в связи с различными обобщениями понятия объема матрицы. К простейшему методу оптимизации функционала от многих переменных относится, конечно, метод последовательной координатной оптимизации. При этом координаты можно объединять в блоки и последовательно оптимизировать по блокам. Цель исследования – построить метод выбора блока, основанный на принципе максимального объема, и, возможно, получить новые эффективные методы оптимизации.

Научная работа: темы и направления в 2020 году

Программа

| Линейная алгебра | Математика

«Предыдущая | Далее »

Видео-введение профессора Стрэнга

Введение в курс линейной алгебры

Обзор курса

Этот курс охватывает теорию матриц и линейную алгебру, уделяя особое внимание темам, полезным в других дисциплинах. Линейная алгебра — это раздел математики, изучающий системы линейных уравнений и свойства матриц.Понятия линейной алгебры чрезвычайно полезны в физике, экономике и социальных науках, естественных науках и технике. Благодаря широкому спектру приложений линейная алгебра является одним из наиболее широко преподаваемых предметов в математике на уровне колледжа (и все чаще в средней школе).

Предварительные требования

18.02 Многопараметрическое исчисление является формальным предварительным условием для студентов MIT, желающих поступить по 18.06 линейной алгебры, но знание математического анализа не требуется для изучения предмета.

Для успешного прохождения этого курса вам необходимо хорошо разбираться в векторах, матрицах и трехмерных системах координат. Этот материал представлен в нескольких первых лекциях 18.02 Multivariable Calculus и снова здесь.

Основные операции линейной алгебры — это те операции, которым вы научились в начальной школе — сложение и умножение для получения «линейных комбинаций». Но с векторами мы перемещаемся в четырехмерное и n-мерное пространство!

Цели курса

После успешного завершения курса вы будете хорошо разбираться в следующих темах и их приложениях:

Системы линейных уравнений
Сокращение строк и эшелонированные формы
Матричные операции, включая обратные
Блок матрицы
Линейная зависимость и независимость
Подпространства, основания и измерения
Ортогональные основания и ортогональные проекции
Процесс Грама-Шмидта
Линейные модели и задачи наименьших квадратов
Детерминанты и их свойства
Правило Крамера
Собственные значения и собственные векторы
Диагонализация матрицы
Симметричные матрицы
Положительно определенные матрицы
Подобные матрицы
Линейные преобразования
Разложение по сингулярным значениям n

Формат

Этот курс, разработанный для самостоятельного изучения, организован таким образом, чтобы следовать последовательности тем, охватываемых курсом линейной алгебры Массачусетского технологического института.Контент организован в три основных блока:

Ax = b и четыре подпространства
Наименьшие квадраты, детерминанты и собственные значения
Положительно определенные матрицы и приложения

Каждый блок был дополнительно разделен на последовательность сеансов, охватывающих сумма, которую вы можете рассчитывать выполнить за один присест. Каждая сессия включает видеолекцию по теме, сопровождаемую кратким изложением лекции. Для дальнейшего изучения предлагаются варианты чтения в учебнике профессора Стрэнга (как 4-е, так и 5-е издания):

Strang, Gilbert.Введение в линейную алгебру. 4-е изд. Уэлсли, Массачусетс: Wellesley-Cambridge Press, февраль 2009 г. ISBN: 9780980232714

Стрэнг, Гилберт. Введение в линейную алгебру. 5-е изд. Уэлсли, Массачусетс: Wellesley-Cambridge Press, февраль 2016 г. ISBN: 9780980232776

Щелкните навигационные ссылки в левом столбце, чтобы отобразить сеансы в трех разделах.

Чтобы помочь вам в обучении, вы увидите, как опытный инструктор Массачусетского технологического института обучает решению проблем (шесть видеороликов по решению проблем также доступны на мандаринском диалекте китайского языка).

Наконец, в рамках каждого раздела вам будут представлены наборы задач в стратегических точках, чтобы вы могли проверить свое понимание материала.

MIT ожидает, что его студенты потратят на этот курс около 150 часов. Более половины этого времени уходит на подготовку к уроку и выполнение заданий. Трудно оценить, сколько времени вам понадобится, чтобы пройти курс, но вы, вероятно, можете рассчитывать потратить час или больше на проработку каждого отдельного занятия.

Познакомьтесь с командой

Этот курс для стипендиатов OCW был разработан:

Гилбертом Странгом, профессором математики Массачусетского технологического института

При технической поддержке и письменной поддержке:

Доктор математики, профессор математики и Компьютерные науки, Бриджуотерский государственный университет

Справочные видеоролики были разработаны:

Мартина Балагович
Линан Чен
Бенджамин Харрис
Ана Рита Пирес
Дэвид Широкофф
Никола Камбуров

Чтобы узнать больше о каждого ТА, посетите страницу Знакомство с ТА.

«Предыдущая | Следующая »

Что такое линейная алгебра? (Краткое введение)

В следующем видео представлен план всех тем, которые вы ожидаете увидеть в типичном классе линейной алгебры College (т. Е. Матричной алгебре).

Все темы подробно освещены в нашем онлайн-курсе линейной алгебры.

Онлайн-курс содержит:

Полные лекции — Предназначены для повышения результатов тестов.
150+ HD Video Library — Больше не нужно тратить время на поиски на YouTube.
Доступен 24/7 — Никогда не беспокойтесь о том, что снова пропустите урок.
Практические экзамены — Убедитесь, что вы готовы к выпускным экзаменам.

Обзор линейной алгебры

Обзор линейной алгебры

Следующие разделы содержат ссылки на наши полные уроки по всем темам линейной алгебры.

Кроме того, не забудьте посмотреть наши БЕСПЛАТНЫЕ обучающие видео по исчислению и прочитать наши обзоры, чтобы увидеть, какие мы из себя представляем.

.a-tab-content> .a-box-inner {padding-top: 5px; padding-bottom: 5 пикселей; }
#mediaTabs_tabSetContainer .a-tab-content {border-radius: 0px; }
#mediaTabsHeadings {white-space: nowrap; переполнение: скрыто; }
# mediaTabsHeadings.nonJSTabs {white-space: normal; }
#mediaTabsHeadings ul.a-tabs {background: # f9f9f9; }
#mediaTabsHeadings .mediaTab_heading .mediaTab_logo {padding-left: 3px; вертикальное выравнивание: базовая линия; }
#mediaTabsHeadings #mediaTabs_tabSet {margin-top: 5px; плыть налево; граница справа: 0 пикселей; }
#mediaTabsHeadings.mediaTab_heading {маржа слева: -1px; }
#mediaTabsHeadings .mediaTab_heading a {color: # 111; граница справа: сплошной 1px #ddd; padding-top: 8 пикселей; padding-bottom: 7 пикселей; }
#mediaTabsHeadings .mediaTab_heading.a-active a {color: # c45500; маржа сверху: -5 пикселей; padding-top: 11 пикселей; граница слева: сплошной 1px #ddd; border-top-width: 3px;}
#mediaTabsHeadings .tabHidden {display: none! important; }
#bookDescription_feature_div {дисплей: встроенный блок; ширина: 100%;}
]]>

В этой новой электронной книге с лазерной фокусировкой, написанной в привычном для вас дружеском стиле Machine Learning Mastery, вы наконец разберетесь с уравнениями, греческими буквами и путаницей и откроете для себя темы линейной алгебры, которые вам необходимо знать.

Используя четкие объяснения, стандартные библиотеки Python и пошаговые учебные уроки, вы узнаете, что такое линейная алгебра, важность линейной алгебры для машинного обучения, векторных и матричных операций, матричной факторизации, анализа главных компонентов и многого другого. более.

Это огромная область исследований, которая оказала влияние на другие области, такие как статистика, а также инженерия и физика. К счастью, нам не нужно знать широту и глубину области линейной алгебры, чтобы лучше понимать и применять машинное обучение.

Мы знаем, что знание линейной алгебры критически важно, но не обязательно с него начинать. Изучение сначала линейной алгебры, затем исчисления, вероятности, статистики и, в конечном итоге, теории машинного обучения — это долгий и медленный восходящий путь.

Разработчикам лучше начать с систематических процедур, которые приносят результаты, и вернуться к более глубокому пониманию теории, используя результаты работы в качестве контекста.Я называю это подходом к машинному обучению «сверху вниз» или «сначала результаты», а линейная алгебра — это не первый шаг, но, возможно, второй или третий.

Линейная алгебра — это обширная область исследований, которая имеет свои корни в инженерии, физике и квантовой физике. Существуют также теоремы и выводы почти для всего, большинство из которых не поможет вам улучшить навыки или глубже понять вашу модель машинного обучения.

Как и само машинное обучение, используйте подход сверху вниз. Вместо того, чтобы начинать с теорем и абстрактных понятий, вы можете изучить основы линейной алгебры конкретным способом с помощью структур данных и отработанных примеров операций с этими структурами данных.Это намного быстрее (и весело).

Я разочарован, увидев практикующего за практиком, погружающегося в учебники линейной алгебры и онлайн-курсов, предназначенных для студентов бакалавриата, и сдающегося. Подход снизу вверх труден, особенно если у вас уже есть работа на полную ставку.

Проблемой для новичков в области линейной алгебры являются такие операции, как умножение матриц и тензорное умножение, которые не реализованы как прямое умножение элементов этих структур и на первый взгляд кажутся неинтуитивными.

Факторизация матрицы — это ключевой инструмент линейной алгебры, который широко используется как элемент многих более сложных операций как в линейной алгебре (например, обратная матрица), так и в машинном обучении (метод наименьших квадратов, PCA, SVD и т. Д.).

Линейная алгебра изначально была разработана для решения систем линейных уравнений. Это уравнения, в которых уравнений больше, чем неизвестных переменных. В результате их сложно решить арифметически, потому что нет единого решения, так как нет линии или плоскости, которые могли бы соответствовать данным без какой-либо ошибки.

Задачи этого типа могут быть сформулированы как минимизация квадратичной ошибки, называемая методом наименьших квадратов, и может быть переработана на языке линейной алгебры, называемом линейным методом наименьших квадратов.

Изучение линейной алгебры, по крайней мере, так, как я преподаю с помощью практических примеров и исполняемого кода, — это очень весело. Как только вы увидите, как операции работают с реальными данными, трудно избежать развития сильной интуиции в отношении методов.

Учебники были разработаны, чтобы научить вас этим методам наиболее быстрым и эффективным способом, который я знаю: , чтобы научиться, выполняя . С исполняемым кодом, который вы можете запустить для развития необходимой интуиции, который вы можете скопировать и вставить в свой проект, и немедленно получит результат .

Линейная алгебра важна для машинного обучения, и я считаю, что если ее преподавать на правильном уровне для практиков, она может быть увлекательным, забавным, непосредственно применимым и неизмеримо полезным набором техник.

Есть много вещей, которые вы можете узнать о линейной алгебре, от теории до абстрактных концепций и API. Моя цель — прямо привести вас к развитию интуиции в отношении элементов, которые вы должны понимать, с помощью учебных пособий, ориентированных на лазер.

Вы можете выполнять уроки по одному в день, по одному в неделю или в своем собственном темпе. Я считаю, что импульс критически важен, и эта книга предназначена для чтения и использования, а не для того, чтобы сидеть сложа руки.

Часть 2: NumPy . Откройте для себя учебные пособия по NumPy, в которых показано, как создавать, индексировать, нарезать и изменять массивы NumPy, основную структуру данных, используемую в машинном обучении, и основу для примеров линейной алгебры в этой книге.

Вы можете видеть, что каждая часть нацелена на определенный результат обучения, как и каждое руководство в каждой части.Это действует как фильтр, чтобы гарантировать, что вы сосредоточены только на вещах, которые вам нужно знать, чтобы получить конкретный результат, и не увязнуть в математике или почти бесконечном количестве отклонений.

Учебники не были разработаны для того, чтобы научить вас всему, что нужно знать о каждой из теорий или методов линейной алгебры. Они были разработаны, чтобы дать вам понимание того, как они работают, как их использовать и как интерпретировать результаты самым быстрым способом, который я знаю: учиться на практике.

Плюс, как и следовало ожидать от любого отличного продукта на рынке, каждая электронная книга для мастерства в машинном обучении
имеет самый верный признак уверенности: мою золотую стандартную 100% гарантию возврата денег.

Я написал книги по алгоритмам, побеждал и занимал высокие места в соревнованиях, консультировал стартапы и много лет проработал в промышленности. (Да, я потратил много времени на создание и поддержку НАСТОЯЩИХ операционных систем!)

Если вам действительно нужна бумажная копия, вы можете приобрести книгу или комплект и создать печатную версию для личного пользования. В файлах PDF нет управления цифровыми правами (DRM), чтобы вы не могли их распечатать.

Ваш адрес электронной почты : адрес электронной почты, который вы использовали для совершения покупки (обратите внимание, он может отличаться от адреса электронной почты, который вы использовали для оплаты через PayPal).

Обратите внимание, что вы получаете бесплатные обновления для всех книг в вашем супер-наборе. Сюда входят исправления ошибок, изменения API и иногда даже новые главы. Я отправляю клиентам электронные письма о крупных обновлениях книг, или вы можете связаться со мной в любое время и попросить последнюю версию книги.

Я пока не рекомендую использовать Keras как часть TensorFlow 2 (например,грамм. тф.керас). Это слишком ново, у новых вещей есть проблемы, и я жду, когда осядет пыль. Автономный Keras работает много лет и продолжает работать очень хорошо.

Есть один случай учебников, которые не поддерживают TensorFlow 2, потому что в них используются сторонние библиотеки, которые еще не были обновлены для поддержки TensorFlow 2. В частности, в руководствах используется Mask-RCNN для распознавания объектов. После обновления сторонней библиотеки эти учебные пособия также будут обновлены.

Книга « Мастер алгоритмов машинного обучения » предназначена как для программистов, так и для непрограммистов. Он учит вас, как работают 10 лучших алгоритмов машинного обучения, с отработанными примерами в арифметике и электронными таблицами, а не кодом. Основное внимание уделяется пониманию того, как каждая модель учится и делает прогнозы.

Книга « Алгоритмы машинного обучения с нуля, » предназначена для программистов, которые учатся, написав код, чтобы понять. Он предоставляет пошаговые инструкции о том, как реализовать лучшие алгоритмы, а также о том, как загружать данные, оценивать модели и многое другое.В нем меньше информации о том, как работают алгоритмы, вместо этого он сосредоточен исключительно на том, как реализовать каждый из них в коде.

Я разрабатываю свои книги как комбинацию уроков и проектов, чтобы научить вас использовать определенный инструмент или библиотеку машинного обучения, а затем применить их к реальным задачам прогнозного моделирования.

Чтобы получить последнюю версию книги, свяжитесь со мной напрямую и сообщите номер вашего заказа или адрес электронной почты для покупки, и я могу повторно отправить электронное письмо с квитанцией о покупке с обновленной ссылкой для загрузки.

В книге «Сети с долгосрочной краткосрочной памятью с Python » подробно рассматриваются LSTM и рассказывается, как подготовить данные, как разработать набор различных архитектур LSTM, настроить параметры, обновить модели и многое другое.

Книга «Глубокое обучение для прогнозирования временных рядов» фокусируется на том, как использовать набор различных моделей глубокого обучения (MLP, CNN, LSTM и гибриды) для решения набора различных задач прогнозирования временных рядов (одномерных, многомерных, многоэтапных и гибридов). комбинации).

Книги обеспечивают более удобную упаковку материала, включая исходный код, наборы данных и формат PDF. Они также включают обновления для новых API-интерфейсов, новые главы, исправление ошибок и опечаток и прямой доступ ко мне для всей поддержки и помощи, которые я могу предоставить.

Вместо этого комиссия была добавлена вашим банком, эмитентом кредитной карты или финансовым учреждением.Это может быть связано с тем, что ваш банк взимает дополнительную плату за онлайн-транзакции или международные транзакции.

Вы можете сосредоточиться на обеспечении ценности машинного обучения, обучаясь и получая хорошие навыки решения задач прогнозного моделирования на всех этапах.Вы можете продемонстрировать это умение, разработав портфолио выполненных проектов машинным обучением.

Мои книги созданы специально для того, чтобы помочь вам в достижении этих целей. Они научат вас, как именно использовать инструменты и библиотеки с открытым исходным кодом для получения результатов в проекте прогнозного моделирования.

Хотя линейная алгебра — это обширная область с множеством эзотерических теорий и открытий, инструменты и обозначения, взятые из этой области, полезны для практиков машинного обучения. Имея прочный фундамент того, что такое линейная алгебра, можно сосредоточиться только на хороших или важных частях.

Линейная алгебра — это линейные комбинации. То есть, используя арифметику для столбцов чисел, называемых векторами, и массивов чисел, называемых матрицами, для создания новых столбцов и массивов чисел. Линейная алгебра — это изучение прямых и плоскостей, векторных пространств и отображений, необходимых для линейных преобразований.

Это относительно молодая область исследования, изначально формализованная в 1800-х годах для поиска неизвестных в системах линейных уравнений. Линейное уравнение — это просто набор терминов и математических операций, некоторые из которых неизвестны; например:

y = 0,1 * x1 + 0,4 * x2

y = 0,3 * x1 + 0,9 * x2

y = 0,2 * x1 + 0,3 * x2

…

Столбец значений y может быть взят как вектор-столбец выходных данных уравнения.Два столбца значений с плавающей запятой являются столбцами данных, скажем, a1 и a2, и могут быть приняты как матрица A. Два неизвестных значения x1 и x2 могут быть приняты как коэффициенты уравнения и вместе образуют вектор неизвестных b предстоит решить. Мы можем записать это компактно, используя обозначения линейной алгебры, как:

Проблемы этой формы обычно сложно решить, потому что неизвестных больше (здесь 2), чем уравнений, которые нужно решить (здесь 3). Кроме того, часто нет единственной линии, которая могла бы без ошибок удовлетворять всем уравнениям.Системы, описывающие часто интересующие нас проблемы (например, линейная регрессия), могут иметь бесконечное количество решений.

Это дает небольшое представление о самой сути линейной алгебры, которая интересует нас, практикующих машинное обучение. Большая часть остальных операций заключается в том, чтобы облегчить понимание и решение этой проблемы и подобных проблем.

Это больше, чем просто реализация операций линейной алгебры в библиотеках кода; он также включает в себя тщательное решение проблем прикладной математики, таких как работа с ограниченной точностью цифровых компьютеров с плавающей запятой.

хороши для выполнения вычислений линейной алгебры, и большая часть зависимости от графических процессоров (GPU) современных методов машинного обучения, таких как глубокое обучение, объясняется их способностью быстро вычислять операции линейной алгебры.

Эффективные реализации векторных и матричных операций были первоначально реализованы на языке программирования FORTRAN в 1970-х и 1980-х годах, и большой объем кода или кода, перенесенного из этих реализаций, лежит в основе большей части линейной алгебры, выполняемой с использованием современных языков программирования, таких как Python.

Часто, когда вы вычисляете операции линейной алгебры прямо или косвенно с помощью алгоритмов более высокого порядка, ваш код, скорее всего, опускается вниз, чтобы использовать одну из этих или аналогичных библиотек линейной алгебры. Название одной из этих базовых библиотек может быть вам знакомо, если вы установили или скомпилировали любую из числовых библиотек Python, таких как SciPy и NumPy.

В своей классической книге по теме под названием «Введение в линейную алгебру» Гилберт Стренг приводит главу, посвященную приложениям линейной алгебры. В нем он демонстрирует определенные математические инструменты, основанные на линейной алгебре. Вкратце это:

Еще одно интересное применение линейной алгебры состоит в том, что это тип математики, используемый Альбертом Эйнштейном в частях его теории относительности.В частности, тензоры и тензорное исчисление. Он также ввел новый тип обозначений линейной алгебры в физику, названный нотацией Эйнштейна, или соглашением Эйнштейна о суммировании.

Линейная алгебра — это онлайн-курс с индивидуальным темпом, эквивалентный первому году курса линейной алгебры колледжа.Этот курс охватывает весь учебный план семестрового очного курса линейной алгебры Джонса Хопкинса с несколькими дополнительными темами. Компьютерные интерактивы, домашние задания и викторины помогают закрепить концепции, преподаваемые в классе. Проекты, охватывающие сложные приложения, познакомят студентов с математическим набором текста с помощью LaTeX. Материалы онлайн-курса дополняют необходимый учебник.

Каждому студенту назначается инструктор CTY, который будет помогать ему во время курса. Студенты могут связаться со своим инструктором по электронной почте с любыми вопросами или проблемами в любое время.Можно запланировать онлайн-обзорные сессии один на один для подготовки к оцениваемым оценкам, которые включают в себя викторины, домашние задания, промежуточные экзамены и кумулятивный финал. Преподаватели используют программное обеспечение виртуального класса, позволяющее использовать видео, голос, текст, совместное использование экрана и интерактивную доску.

Для зачисления, начинающегося 1 января 2019 г. или позднее, на этот курс требуется наблюдатель, если цель студента — получить оценку.Пожалуйста, ознакомьтесь с требованиями к проктору для получения более подробной информации.

Для этого курса требуется правильно обслуживаемый компьютер с высокоскоростным доступом в Интернет и современный веб-браузер (например, Chrome или Fire Fox).Студент должен иметь возможность общаться с инструктором по электронной почте. Посетите страницу «Технические требования и поддержка» для получения более подробной информации.

Виртуальный онлайн-класс Zoom
В этом курсе используется виртуальный онлайн-класс, который можно использовать для общения преподавателя и ученика, если у ученика есть какие-либо вопросы по курсу или учебной программе. Класс работает на стандартных компьютерах с настольным клиентом Zoom, а также на планшетах или портативных устройствах, поддерживающих приложение Zoom Mobile.Студентам понадобится компьютер с установленным настольным клиентом Zoom для просмотра любых записанных встреч. Настольный клиент Zoom и мобильное приложение Zoom доступны для бесплатной загрузки.

Алтьери, М., и Ширмер, Э. (2019). Изучение концепции собственных значений и собственных векторов: сравнительный анализ достигнутой концепции построения в линейной алгебре с использованием теории APOS среди студентов с разным образованием. ZDM Mathematics Education ( в этом выпуске ).

Эндрюс-Ларсон, К., Вавро, М., и Занди, М. (2017). Гипотетическая траектория обучения для концептуализации матриц как линейных преобразований. Международный журнал математического образования в науке и технологиях, 48 (6), 809–829. https://doi.org/10.1080/0020739X.2016.

Айдын, С.(2014). Использование генерации примеров для изучения понимания учащимися концепций линейной зависимости / независимости в линейной алгебре. Международный журнал математического образования в науке и технологиях, 45 (6), 813–826.

Белтран-Мену, М. Дж., Мурильо-Арсила, М., и Альбаррасин, Л. (2016). Акцент на визуализации и физических приложениях при изучении собственных векторов и собственных значений. Преподавание математики и ее приложений: Международный журнал IMA, 36 (3), 123–135. https://doi.org/10.1093/teamat/hrw018.

Чаглаян, Г.(2015). Осмысление отношений собственное значение-собственный вектор: взаимосвязи линейной алгебры и геометрии математиков в динамической среде. Журнал математического поведения, 40, 131–153. https://doi.org/10.1016/j.jmathb.2015.08.003.

Каркамо А., Фортуни Дж. И Гомес В. (2017). Математическое моделирование и траектория обучения: инструменты для поддержки обучения линейной алгебре. Международный журнал математического образования в науке и технологиях , 48 (3), 338–352.

Доган-Данлэп, Х. (2010). Способ рассуждений студентов, изучающих линейную алгебру: Геометрические представления. В специальном выпуске , посвященном 15-й конференции ILAS в Канкуне, Мексика, 16–20 июня 2008 г. (том 432 (8), стр. 2141–2159). https://doi.org/10.1016/j.laa.2009.08.037

Домингес-Гарсия, С., Гарсия-Плана, М. И., и Таберна, Дж. (2016). Математическое моделирование в инженерии: альтернативный способ обучения линейной алгебре. Международный журнал математического образования в науке и технологиях, 47 (7), 1076–1086. https://doi.org/10.1080/0020739X.2016.1153736.

Дубинский, Э., и Макдональд, М. (2001). APOS: конструктивистская теория обучения в исследованиях в области математического образования. In D. Holton., M. Artigue, U. Krichgraber, J. Hillel, M. Niss & A. Schoenfeld (Eds.), Преподавание и изучение математики на университетском уровне: Международная комиссия по изучению математического обучения ( С. 273–280). Дордрехт: Kluwer Academic Publishers.

Эртекин, Э., Солак, С., & Язычи, Э. (2010) Влияние формализма на алгебраическую и геометрическую интерпретацию понятий линейной зависимости / независимости обучаемыми учителями. Международный журнал математического образования в науке и технологиях , 41 (8), 1015–1035.

Фриман, С., Эдди, С. Л., Макдонаф, М., Смит, М. К., Окороафор, Н., Джордт, Х. и др. (2014). Активное обучение повышает успеваемость учащихся в области естественных наук, инженерии и математики. Proceedings of the National Academy of Sciences, 111 (23), 8410–8415.

Ханна, Дж., Стюарт, С., и Томас, М. О. Дж. (2016). Развитие концептуального понимания и ясности определений в линейной алгебре через три мира математического мышления. Преподавание математики и ее приложений: Международный журнал IMA, 35 (4), 216–235. https://doi.org/10.1093/teamat/hrw001.

Харел, Г. (2018). Изучение и преподавание линейной алгебры через призму интеллектуальной потребности и эпистемологического обоснования и их составляющих.В С. Стюарт, К. Эндрюс-Ларсон, А. Берман и М. Зандие (ред.), Проблемы и стратегии обучения линейной алгебре (стр. 3–27). Дордрехт: Спрингер.

Лаурсен, С.Л., Хасси, М. Л., Коган, М., и Уэстон, Т. Дж. (2014). Преимущества для женщин и мужчин основанного на запросе обучения математике в колледже: исследование, проведенное несколькими учреждениями. Журнал исследований в области математического образования, 45 (4), 406–418.

Нисидзава, Х., Кимура, К., Оно, В., и Йошиоко, Т. (2014). Интерактивные рабочие листы для соединения символьных и визуальных представлений трехмерных векторных уравнений. Преподавание математики и ее приложений: Международный журнал IMA, 33 (1), 52–64. https://doi.org/10.1093/teamat/hru005.

Plaxco, D., Zandieh, M., & Wawro, M. (2018). Направления растяжения и факторы растяжения: последовательность, предназначенная для поддержки управляемого переосмысления собственного вектора и собственного значения. В С. Стюарт, К. Эндрюс-Ларсон, А. Берман и М. Занди (ред.), Проблемы в обучении линейной алгебре. Монографии ICME-13 (стр. 175–193). Чам: Спрингер.

Расмуссен, К., & Вавро, М. (2017). Пост-математическое исследование в высшем математическом образовании. В J. Cai (Ed.), Сборник исследований в области математического образования (стр. 551–579). Рестон: Национальный совет учителей математики.

Штульманн, А. (2019). Студенты-математики разговаривают друг с другом: появление неоднозначностей в конструкциях доказательства линейной алгебры, включающих количественную оценку уникальности. ZDM Mathematics Education ( в этом выпуске ).

Тригуэрос, М. (2018). Изучение линейной алгебры с использованием моделей и концептуальной деятельности.В С. Стюарт, К. Эндрюс-Ларсон, А. Берман и М. Занди (ред.), Проблемы в обучении линейной алгебре. Монографии ICME-13 (стр. 20–50). Чам: Спрингер.

Вавро, М., Расмуссен, К., Зандие, М., и Ларсон, К. (2013a). Исследование дизайна в рамках высшего математического образования: пример из вводной линейной алгебры. В T. Plomp & N. Nieveen (Eds.), Исследование образовательного дизайна — Часть B: Иллюстративные примеры (стр. 905–925). Энсхеде: Нидерланды: SLO.

Апрель 2024
Пн	Вт	Ср	Чт	Пт	Сб	Вс
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

Темы линейная алгебра: темы, основы, методы, применение, примеры

Тема: Линейная алгебра и аналитическая геометрия

Содержние дисциплины «Линейная алгебра» : Кафедра МЭО : АлтГТУ

Иллюстративный видеокурс по линейной алгебре: 11 уроков

ТЕМА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ И ЛИНЕЙНОЙ АЛГЕБРЫ

Введение в линейную алгебру

ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Алгебра и аналитическая геометрия

1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

ЛЕКЦИИ ПО ВЫСШЕЙ АЛГЕБРЕ

Лекция 28 Глава 1.

РАЗДЕЛ 1. Линейная алгебра.

Лекция 6. Геометрические векторы.

ЛИНЕЙНАЯ АЛГЕБРА ВМЕСТЕ С MAPLE

Глава 1. Элементы линейной алгебры.

1. Требования к знаниям, умениям, навыкам

УДК [ ](075.

Тема: Системы линейных уравнений

Высшая математика для психологов

Аналитическая геометрия. Лекция 1.3

Глава 4. Матрицы. Лекция Основные понятия.

Практикум по линейной алгебре

1.

ЛИНЕЙНАЯ АЛГЕБРА. ЧАСТЬ I

МАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА

ПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.

Глава 1. Начала линейной алгебры

Геометрические векторы

Список литературы на тему: Линейная алгебра

СПИСОК ЛИТЕРАТУРЫ

Банк тестовых заданий по курсу «Линейная алгебра» Текст научной статьи по специальности «Науки об образовании»

Вычислительная линейная алгебра

Научная работа: темы и направления в 2020 году

| Линейная алгебра | Математика

Видео-введение профессора Стрэнга

Введение в курс линейной алгебры

Обзор курса

Предварительные требования

Цели курса

Формат

Познакомьтесь с командой

Что такое линейная алгебра? (Краткое введение)

Обзор линейной алгебры

Получите доступ ко всем курсам и более 150 HD-видео по подписке

Еще не готовы подписаться? Испытайте Calcworkshop на нашем БЕСПЛАТНОМ курсе с лимитами

Кырчей, Иван: 9781536177701: Амазонка.com: Книги

Линейная алгебра для машинного обучения

Откройте для себя математический язык данных в Python

Ясные и полные примеры.

Почему линейная алгебра?

Разочарованы математикой?

Тензор !?

Почему линейная алгебра важна для машинного обучения?

3 ошибки начинающих

1.Новички слишком рано изучают линейную алгебру

2. Новички слишком много изучают линейную алгебру

3. Новички изучают линейную алгебру неправильно

Лучший способ освоить линейную алгебру

5 областей линейной алгебры, на которых следует сосредоточиться

1. Изучите нотацию линейной алгебры

2. Изучите арифметику линейной алгебры

3. Изучение линейной алгебры для статистики

4. Изучите матричную факторизацию

5. Изучение метода наименьших квадратов

Причина бонуса

Представляем мою новую электронную книгу: «

Для кого эта книга?

Что делать, если я новичок в машинном обучении?

Что делать, если я просто разработчик?

Что делать, если моя математика действительно плохая?

Что делать, если я не программист на Python?

Что делать, если я прохожу курс линейной алгебры в университете?

О ваших результатах

Прочитав и проработав эту книгу, вы узнаете:

Прочитав эту книгу, вы сможете:

Что именно написано в этой книге?

Обзор уроков

Фонд

NumPy

Матрицы