64 в степени 3: Онлайн калькулятор степеней. Возведение в степень онлайн.

Содержание

Возведение в степень и извлечение корня из числа онлайн.

Корень из числа

Корень нечётной степени из положительного числа

В результате вычисления корня нечётной степени из положительного числа будет положительное число: .

Пример Вычислим корни нечётной степени из 8, 27, 125, 243

Корни 3 степени также называют кубическими корнями.

В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.

Корень нечётной степени из отрицательного числа

В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .

Пример Найдем корни 3 и 5 степеней из отрицательных чисел.

Корень четной степени из положительного числа

Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .

Пример Вычислим корни 2 и 4 степени.

Корень 2-й степени называют квадратный корнем.

Корень четной степени из отрицательного числа

Корень четной степени из отрицательного числа не существует для вещественных чисел.

Корень любой степени из нуля

Числа в степени -1, 0, 1

Число в -1 степени

Число 3 в -1 степени можно представить в виде дроби .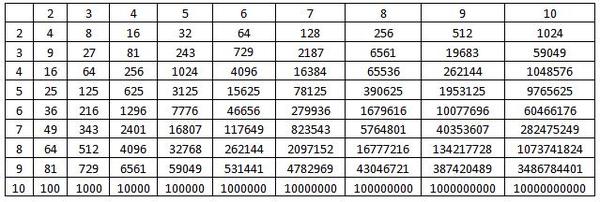 Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.

Число является обратным числом 5, т.е. их произведение равно единице , такое равенство выполнено для любого числа

Пример Представить дробь в степени -1

Число в 1 степени

Число в первой степени является самим числом a¹=a

Число в 0 степени

Любое число в степени ноль равно единице a⁰=1

Калькулятор степеней

Онлайн калькулятор помогает возвести число в любую степень и найти корень любой степени из числа (квадратные, кубические корни, а также корни других степеней). Основанием степени могут быть любые числа, показателем степени также может быть любые числа, в том числе и отрицательные.

Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.

Как возвести число в степень?

Чтобы возвести число X в степень n, достаточно всего лишь умножить число X его само на себя n раз.

Что такое отрицательная степень числа?

Отрицательная степень числа — это единица, поделённая на число в степени n, то есть a^-n = 1/ aⁿ.

Основные действия со степенями

Число 3⁴— это 3×3×3×3, где перемножаются четыре одинаковых множителя. Если умножить 3⁴ на 3², то мы получим (3×3×3×3)×(3×3), то есть 3⁶. Отсюда первое правило возведения в степень: при умножении чисел, возведенных в степень, их показатели суммируются. Математически: x^m * xⁿ = x^(m+n).
Число 3⁵разделить на 3², это означает следующее: (3×3×3×3×3)/(3×3), то есть останется (3×3×3) или 3³.Отсюда второе правило действий со степенями: при делении чисел, возведенных в степень, их показатели вычитаются. Математически: x^m / xⁿ = x^(m-n).
Число 5⁴возвести в куб, то есть в третью степень. Для этого нужно вычислить выражение (5×5×5×5)×(5×5×5×5)×(5×5×5×5). Получилось 12 сомножителей. Отсюда третье правило: при возведении в n-ную степень числа в степени m, показатели перемножаются. Математически: (x^m)ⁿ = x^(m×n).
Любое положительное число в степени 0 всегда равно единице. Математически: x⁰= 1. Например можно представить 7⁰как 7⁴ разделить на 7⁴ или 7⁴/7⁴=1.
При возведении числа в отрицательную степень необходимо единицу разделить на число в положительной степени. Например, если разделить 8²на 8⁴, то получим 8^-2 или (8×8)/(8×8×8×8). Если сократить восьмерки в числителе и знаменателе, то получим 1/(8×8). Математически: x^-m = 1 / x^m.
Если в качестве степени выступает дробное число, то знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически: x^(m/n)есть корень n-ной степени из x^m. Например, 4^(2/3) означает, что нужно найти корень третьей степени от числа 4².

Навигация по записям

Калькулятор логарифмов онлайн

Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12), для ввода обыкновенных дробей воспользуйтесь знаком «/» (например, 1/2 или 3/4).

Как решать логарифмы

Логарифм обозначается как log_a b и такая запись читается как: логарифм b по основанию a.

При решении логарифмов следует учитывать что, числа a и b должны быть больше 0 и a не должно быть равно 1.

log_a b существует при a > 0, a ≠ 1, b > 0

Логарифмы у которых основание a равно 2, 10 или числу e получили свои названия:

log_e b у которого основание равно числу Эйлера e (е = 2.7182818284…) называется – натуральный и обозначается ln b.
Например, ln 4 это тоже что log_e 4, просто сама запись ln говорит что
основание равно числу e и поэтому запись сокращают.

log₁₀ b у которого основание равно 10 называется – десятичный и обозначается lg b. Например, lg 6, что тоже самое что log₁₀ 6

log₂ b у которого основание равно 2 называется – двоичный и обозначается lb b, такие логарифмы часто используется в информатике. Например, lb 3, это тоже самое что log₂ 3.

Можно легко определить является логарифм log_a b отрицательным или положительным, для этого существует правило: если 0 1 и 0 1
тогда логарифм отрицательный, в остальных случаях положительный

log_a b 1 и 0 1

Например, эти логарифмы будут отрицательными log_1/3 4, log₄ 1/3, log_2/3 5, log₅ 2/3 и т.д. То есть либо a либо b должны быть меньше единицы но не оба сразу.

Найти логарифм означает найти показатель степени, в которую необходимо возвести число a, чтобы получить число b.
Говоря простым языком, когда мы вычисляем логарифм то всегда находим степень, и если возвести число a в эту степень получим число b.

Обозначим за х искомую степень числа a, тогда можно записать следующее уравнение: a^x = b

Приведем примеры:

Дан логарифм log₄ 64, нам необходимо найти такой показатель степени, что при возведении в нее числа 4 должно получиться 64. Запишем уравнение:
4^x = 64

4^x = 4³

х = 3

Проверим, возведем число 4 в степень 3: 4³ = 64.

Вообще любое значение логарифма всегда просто проверить, достаточно число а возвести в степень, равную значению логарифма и если результат будет равен числу b, то ответ верный.

Степень с натуральным показателем

Предварительные навыки

Что такое степень?

Степенью называют произведение из нескольких одинаковых множителей. Например:

2 × 2 × 2

Значение данного выражения равно 8

2 × 2 × 2 = 8

Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется.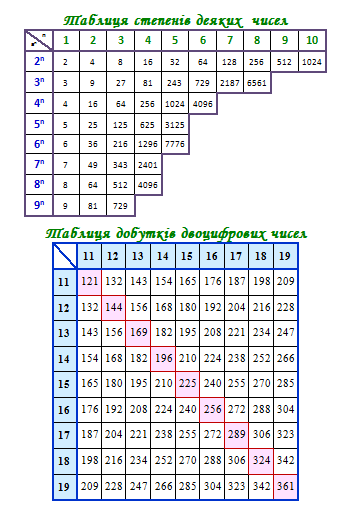 Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:

2³ = 8

Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».

Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.

Например, если дано выражение 5³, то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5.

Число, которое повторяется называют основанием степени. В выражении 5³основанием степени является число 5.

А число, которое надписано над числом 5 называют показателем степени. В выражении 5³показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза

Саму операцию перемножения одинаковых множителей называют возведением в степень.

Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:

Видим, что число 2 в четвёртой степени есть число 16.

Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.

Вообще, определение степени с натуральным показателем выглядит следующим образом:

Степень числа a с натуральным показателем n — это выражение вида aⁿ, которое равно произведению n множителей, каждый из которых равен a

Примеры:

Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.

Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25

Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2

Получилась ошибка, поскольку число 5 во второй степени не равно 10.

Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:

Например, число 5 в первой степени есть само число 5

Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.

Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1

А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:

А выражение 0⁰ не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 0⁰ может иметь смысл.

Для тренировки решим несколько примеров на возведение чисел в степени.

Пример 1. Возвести число 3 во вторую степень.

Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3

3² = 3 × 3 = 9

Пример 2. Возвести число 2 в четвертую степень.

Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2

2⁴ =2 × 2 × 2 × 2 = 16

Пример 3. Возвести число 2 в третью степень.

Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2

2³ =2 × 2 × 2 = 8

Возведение в степень числа 10

Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.

Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2

10²

Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени

10² = 100

Значит, число 10 во второй степени это число 100.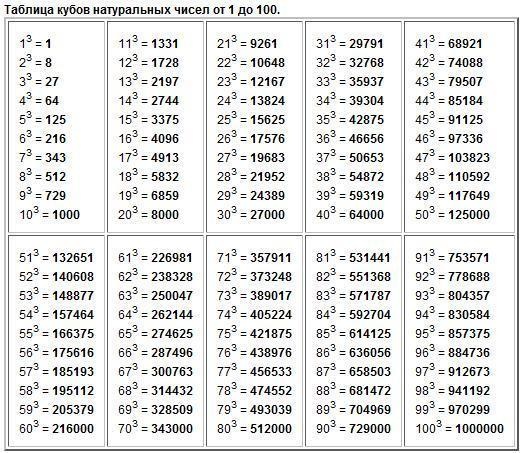 Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10

10² = 10 × 10 = 100

Пример 2. Возведём число 10 в третью степень.

В данном случае после единицы будут стоять три нуля:

10³ = 1000

Пример 3. Возведем число 10 в четвёртую степень.

В данном случае после единицы будут стоять четыре нуля:

10⁴ = 10000

Пример 4. Возведем число 10 в первую степень.

В данном случае после единицы будет стоять один нуль:

10¹ = 10

Представление чисел 10, 100, 1000 в виде степени с основанием 10

Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.

Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 10¹

10 = 10¹

Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 10²

100 = 10²

Пример 3. Представим число 1 000 в виде степени с основанием 10.

1 000 = 10³

Пример 4. Представим число 10 000 в виде степени с основанием 10.

10 000 = 10⁴

Возведение в степень отрицательного числа

При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.

Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)

(−2)² = (−2) × (−2) = 4

Если бы мы не заключили в скобки число −2, то получилось бы что мы вычисляем выражение −2², которое не равно 4. Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.

Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.

Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.

В случае с выражением −2² происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.

Поэтому выражение −2² вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2

Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4

−2² = −4

Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2)² сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.

Пример 2. Возвести число −2 в третью степень.

Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)

(−2)³ = (−2) × (−2) × (−2) = −8

Пример 3. Возвести число −2 в четвёртую степень.

Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)

(−2)⁴ = (−2) × (−2) × (−2) × (−2) = 16

Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.

Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3

В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.

Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.

Пример 7. Возвести число −5 в третью степень.

Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:

(−5)³ = (−5) × (−5) × (−5) = −125

Пример 8. Возвести число −4 в четвёртую степень.

Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:

(−4)⁴ = (−4) × (−4) × (−4) × (−4) = 256

Нахождение значений выражений

При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.

Пример 1. Найти значение выражения 2 + 5²

Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2

2 + 5² = 2 + 25 = 27

Пример 10. Найти значение выражения −6² × (−12)

Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:

−6² × (−12) = −36 × (−12)

Завершаем пример, умножив −36 на (−12)

−6² × (−12) = −36 × (−12) = 432

Пример 11. Найти значение выражения −3 × 2²

Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3

−3 × 2² = −3 × 4 = −12

Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.

Пример 12. Найти значение выражения (3² + 1 × 3) − 15 + 5

Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3. Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:

(3² + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2

Пример 13. Найти значение выражения 2 × 5³ + 5 × 2³

Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:

2 × 5³ + 5 × 2³ = 2 × 125 + 5 × 8 = 250 + 40 = 290

Тождественные преобразования степеней

Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.

Допустим, потребовалось вычислить выражение (2³)². В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.

(2³)²это произведение двух степеней, каждая из которых равна 2³

При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2

Получили произведение 2 × 2 × 2 × 2 × 2 × 2, которое равно 64. Значит значение выражения (2³)² или равно 64

Этот пример можно значительно упростить. Для этого показатели выражения (2³)² можно перемножить и записать это произведение над основанием 2

Получили 2⁶. Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64

Данное свойство работает по причине того, что 2³ это произведение 2 × 2 × 2, которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 2⁶

Вообще, для любого основания a с показателями m и n, выполняется следующее равенство:

(aⁿ)^m = a^n × m

Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают».

После перемножения показателей, получится другая степень, значение которой можно найти.

Пример 2. Найти значение выражения (3²)²

В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:

Получили 3⁴. А число 3 в четвёртой степени есть 81

Рассмотрим остальные преобразования.

Умножение степеней

Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.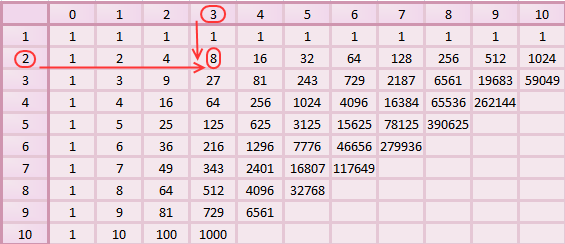

Например, умножим 2² на 3³.

2² это число 4, а 3³ это число 27. Перемножаем числа 4 и 27, получаем 108

2² × 3³ = 4 × 27 = 108

В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.

Например, умножим 2² на 2³

В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 2² и 2³. Иными словами, основание оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:

Получили 2⁵. Число 2 в пятой степени есть 32

Данное свойство работает по причине того, что 2² это произведение 2 × 2, а 2³ это произведение 2 × 2 × 2. Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2.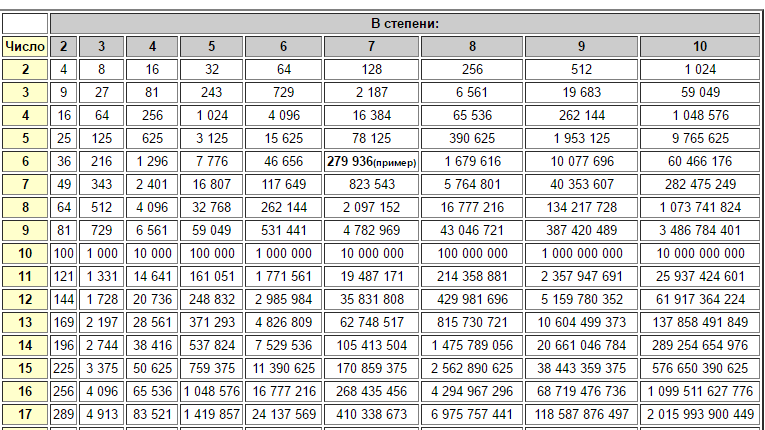 Это произведение представимо в виде 2⁵

Вообще, для любого a и показателей m и n выполняется следующее равенство:

Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: «При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают».

Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.

Например, найдем значение выражения 2¹ × 2² × 2³. Основание 2 оставим без изменений, а показатели сложим:

В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.

Пример 1. Представить в виде степени выражение 5⁸ × 25

В данной задаче нужно сделать так, чтобы вместо выражения 5⁸ × 25 получилась одна степень.

Число 25 можно представить в виде 5². Тогда получим следующее выражение:

В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:

Задачу можно считать решённой, поскольку мы представили выражение 5⁸ × 25 в виде одной степени, а именно в виде степени 5¹⁰.

Запишем решение покороче:

Пример 2. Представить в виде степени выражение 2⁹ × 32

Число 32 можно представить в виде 2⁵. Тогда получим выражение 2⁹ × 2⁵. Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:

Пример 3. Вычислите произведение 3 × 3, используя основное свойство степени.

Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?

Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 3¹ и 3¹

3¹ × 3¹

Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:

3¹ × 3¹ = 3²

Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9

3¹ × 3¹ = 3² = 9

Пример 4. Вычислите произведение 2 × 2 × 3² × 3³, используя основное свойство степени.

Произведение 2 × 2 заменим на 2¹ × 2¹, затем на 2^1 + 1, а затем на 2². Произведение 3² × 3³ заменим на 3^2 + 3, а затем на 3⁵

Далее вычисляем значение каждой степени и находим произведение:

Пример 5. Выполнить умножение x × x

Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:

Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.

Решение данного примера желательно записать так:

Пример 6. Выполнить умножение x² × x

Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

Пример 7. Выполнить умножение y³y²y

Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

Пример 8. Выполнить умножение aa³a²a⁵

Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

Пример 9. Представить степень 3⁸ в виде произведения степеней с одинаковыми основаниями.

В данной задаче нужно составить произведение степеней, основания которых будут равны 3, и сумма показателей которых будет равна 8. Можно использовать любые показатели. Представим степень 3⁸ в виде произведения степеней 3⁵ и 3³

В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 3⁵ × 3³ можно записать как 3^5 + 3, откуда 3⁸.

Конечно можно было представить степень 3⁸ в виде произведения других степеней. Например, в виде 3⁷ × 3¹, поскольку это произведение тоже равно 3⁸

Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.

Пример 10. Представить степень x¹² в виде различных произведений степеней с основаниями x.

Воспользуемся основным свойство степени. Представим x¹² в виде произведений с основаниями x, и сумма показателей которых равна 12

Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:

Возведение в степень произведения

Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.

Например, возведём во вторую степень произведение 2 × 3. Возьмём в скобки данное произведение и в качестве показателя укажем 2

Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:

Принцип работы данного правила основан на определении степени, которое было дано в самом начале.

Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:

2 × 3 × 2 × 3

От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:

2 × 2 × 3 × 3

Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 2², а произведение 3 × 3 можно заменить на 3². Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 2² × 3².

Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n, нужно по отдельности возвести множители a и b в указанную степень n

Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:

Пример 2. Найти значение выражения (2 × 3 × 4)²

В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4. Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:

Пример 3. Возвести в третью степень произведение a × b × c

Заключим в скобки данное произведение, и в качестве показателя укажем число 3

Далее возводим в третью степень каждый множитель данного произведения:

Пример 4. Возвести в третью степень произведение 3xyz

Заключим в скобки данное произведение, и в качестве показателя укажем 3

(3xyz)³

Возведём в третью степень каждый множитель данного произведения:

(3xyz)³ = 3³x³y³z³

Число 3 в третьей степени равно числу 27. Остальное оставим без изменений:

(3xyz)³ = 3³x³y³z³ = 27x³y³z³

В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.

Например, вычислим значение выражения 5² × 3². Возведем каждое число во вторую степень и перемножим полученные результаты:

5² × 3² = 25 × 9 = 225

Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3)². Далее вычислить значение в скобках и возвести полученный результат во вторую степень:

5² × 3² = (5 × 3)² = (15)² = 225

В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b)ⁿ = aⁿ × bⁿ, то aⁿ × bⁿ= (a × b)ⁿ. То есть левая и правая часть равенства поменялись местами.

Возведение степени в степень

Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.

При возведении степени в степень основание оставляют без изменений, а показатели перемножают:

(aⁿ)^m = a^n × m

К примеру, выражение (2³)² является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:

(2³)² = 2^3 × 2 = 2⁶

Далее вычислить степень 2⁶, которая равна 64

(2³)² = 2^3 × 2 = 2⁶ = 64

Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.

Вернёмся к выражению (2³)². Выражение в скобках 2³ представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (2³)² степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.

(2 × 2 × 2)²

А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:

(2 × 2 × 2)² = 2² × 2² × 2²

Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:

(2 × 2 × 2)² = 2² × 2² × 2² = 2^{2 + 2 + 2} = 2⁶

Как и раньше получили 2⁶. Значение этой степени равно 64

(2 × 2 × 2)² = 2² × 2² × 2² = 2^{2 + 2 + 2} = 2⁶ = 64

В степень также может возводиться произведение, сомножители которого тоже являются степенями.

Например, найдём значение выражения (2² × 3²)³. Здесь показатели каждого множителя нужно умножить на общий показатель 3. Далее найти значение каждой степени и вычислить произведение:

(2² × 3²)³= 2^2×3 × 3^2×3 = 2⁶× 3⁶ = 64 × 729 = 46656

Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.

Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:

Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 2¹ × 4¹. А это есть возведение степени в степень.

Перепишем решение с помощью правила возведения степени в степень.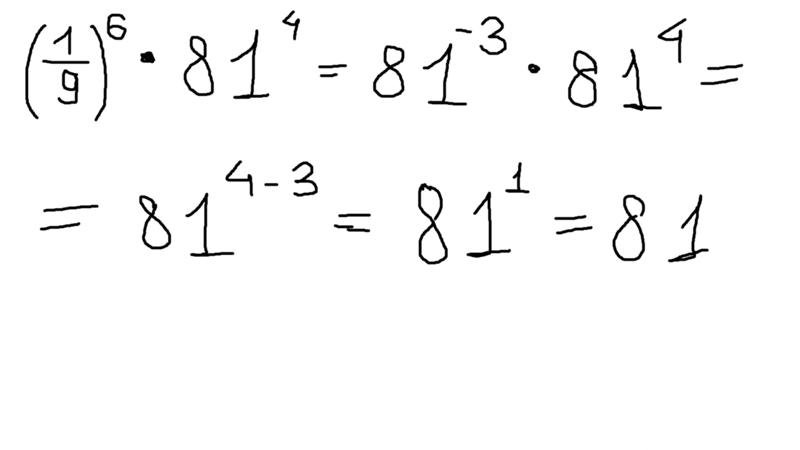 У нас должен получиться тот же результат:

Пример 2. Найти значение выражения (3³)²

Основание оставляем без изменений, а показатели перемножаем:

Получили 3⁶. Число 3 в шестой степени есть число 729

Пример 3. Выполнить возведение в степень в выражении (xy)³

Возведём в третью степень каждый множитель произведения:

Пример 4. Выполнить возведение в степень в выражении (abc)⁵

Возведём в пятую степень каждый множитель произведения:

Пример 5. Выполнить возведение в степень в выражении (−2ax)³

Возведём в третью степень каждый множитель произведения:

Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.

Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2)³ — получится −8.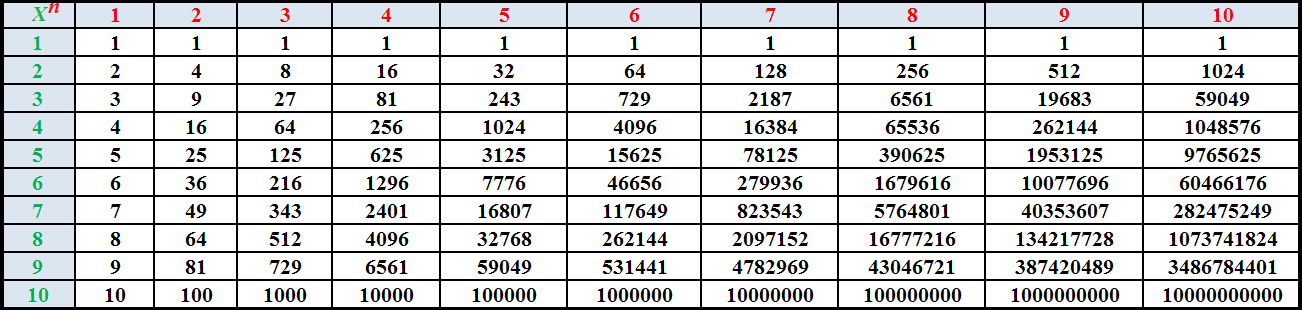 Буквенная часть останется без изменений:

Пример 6. Выполнить возведение в степень в выражении (10xy)²

Пример 7. Выполнить возведение в степень в выражении (−5x)³

Пример 8. Выполнить возведение в степень в выражении (−3y)⁴

Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴

Пример 10. Упростите выражение x⁵ × (x²)³

Степень x⁵ пока оставим без изменений, а в выражении (x²)³ выполним возведение степени в степени:

x⁵ × (x²)³ = x⁵ × x^2 × 3 = x⁵ × x⁶

Теперь выполним умножение x⁵× x⁶. Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:

x⁵ × (x²)³ = x⁵ × x^2× 3 = x⁵ × x⁶ = x^5 + 6 = x¹¹

Пример 9. Найти значение выражения 4³ × 2², используя основное свойство степени.

Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.

Посмотрим внимательно на степень 4³. Основание у этой степени есть число 4, которое можно представить в виде 2². Тогда исходное выражение примет вид (2²)³ × 2². Выполнив возведение степени в степень в выражении (2²)³, мы получим 2⁶. Тогда исходное выражение примет вид 2⁶ × 2², вычислить которое можно, используя основное свойство степени.

Запишем решение данного примера:

Деление степеней

Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.

Например, разделим 4³ на 2².

Вычислим 4³, получим 64. Вычислим 2², получим 4. Теперь разделим 64 на 4, получим 16

Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.

Например, найдем значение выражения 2³ : 2²

Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Значит, значение выражения 2³ : 2² равно 2.

Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.

Вернемся к предыдущему примеру 2³ : 2². Здесь делимое это 2³, а делитель 2².

Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.

В нашем случае, разделить 2³ на 2² означает найти такую степень, которая при умножении на делитель 2² даст в результате 2³. А какую степень можно умножить на 2², чтобы получить 2³ ? Очевидно, что только степень 2¹. Из основного свойства степени имеем:

Убедиться, что значение выражения 2³ : 2² равно 2¹ можно непосредственно вычислив само выражение 2³ : 2². Для этого сначала найдём значение степени 2³, получим 8. Затем найдём значение степени 2², получим 4. Разделим 8 на 4, получим 2 или 2¹, поскольку 2 = 2¹.

2³ : 2² = 8 : 4 = 2

Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:

Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.

Например, найдём значение выражения 2² : 2². Вычислим значение каждой степени и выполним деление получившихся чисел:

При решении примера 2² : 2² также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 2² и 2² равна нулю:

В математике принято считать, что любое число в нулевой степени есть единица:

Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 2² : 2² обычным методом, не используя правило деления степеней, получится единица.

Пример 2. Найти значение выражения 4¹² : 4¹⁰

Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

4¹² : 4¹⁰ = 4^{12 − 10} = 4² = 16

Пример 3. Представить частное x³ : x в виде степени с основанием x

Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:

Пример 4. Представить частное x³ : x² в виде степени с основанием x

Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:

Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x³ можно записать как x × x × x, а степень x² как x × x. Тогда конструкцию x^3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x

Или ещё короче:

Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x². Чтобы сократить дробь на x² нужно числитель и знаменатель дроби разделить на x²

Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:

Или ещё короче:

Пример 5. Выполнить деление x¹² : x³

Запишем решение при помощи сокращения дроби. Деление степеней x¹² : x³ запишем в виде . Далее сократим данную дробь на x³.

Пример 6. Найти значение выражения

В числителе выполним умножение степеней с одинаковыми основаниями:

Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Завершаем пример, вычислив степень 7²

Пример 7. Найти значение выражения

Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (2³)⁴

Теперь выполним в числителе умножение степеней с одинаковыми основаниями:

Теперь применяем правило деления степеней с одинаковыми основаниями:

Значит, значение выражения равно 16

В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.

Например, найдём значение выражения . Степень 4³ запишем в виде возведения степени в степень (2²)³. Тогда получим следующее выражение:

В числителе выполним возведение степени в степень. Сделать это нужно с выражением (2²)³

В числителе и в знаменателе получившегося выражения содержится степень 2⁶, которую можно сократить на 2⁶

Видим, что в результате осталась единственная степень 3², значение которой равно 9.

Пример 8. Найти значение выражения

В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 7⁵ × 4⁵ можно представить в виде степени с одним показателем (7 × 4)⁵. Далее перемножим выражение в скобках, получим 28⁵. В результате исходное выражение примет следующий вид:

Теперь можно применить правило деления степеней:

Значит, значение выражения равно 28. Запишем решение полностью:

Возведение в степень обыкновенных дробей

Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.

Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2

Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как .

Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:

Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности

Значит обыкновенная дробь во второй степени равна дроби .

Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна

Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:

А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 2² и 3² соответственно:

Откуда и получится ответ .

Вообще, для любого a и b ≠ 0 выполняется следующее равенство:

Это тождественное преобразование называют возведением в степень обыкновенной дроби.

Пример 2. Возвести дробь в третью степень

Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:

Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.

Например, возведём дробь во вторую степень:

Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:

Ответ положителен по причине того, что выражение представляет собой произведение двух сомножителей, каждый из которых равен дроби

А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:

Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:

Здесь ответ отрицателем по причине того, что выражение представляет собой произведение трёх множителей, каждый из которых равен дроби

Сначала перемножили и , получили , но затем умножив на мы получим отрицательный ответ

Пример 3. Найти значение выражения

Выполним возведение в степень обыкновенной дроби:

Далее вычислим значение получившегося выражения:

Возведение в степень десятичных дробей

При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5

Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:

Пример 2. Найти значение степени (−1,5)³

Показатель степени является нечётным числом. Значит ответ будет отрицательным

Пример 3. Найти значение степени (−2,4)²

Показатель степени является чётным числом. Значит ответ будет положительным:

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

Решение:

Задание 2. Найдите значение выражения:

Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:

Задание 5. Найдите значение выражения:

Решение:

Задание 6. Найдите значение выражения:

Решение:

Задание 7. Представьте в виде степени произведение:

Решение:

Задание 8. Представьте в виде степени произведение:

Решение:

Задание 9. Представьте в виде степени произведение:

Решение:

Задание 10. Представьте в виде степени произведение:

Решение:

Задание 11. Представьте в виде степени произведение:

Решение:

Задание 12. Представьте в виде степени произведение:

Решение:

Задание 13. Представьте в виде степени частное:

Решение:

Задание 14. Представьте в виде степени частное:

Решение:

Задание 15. Представьте в виде степени частное:

Решение:

Задание 16. Представьте в виде степени частное:

Решение:

Задание 17. Представьте в виде степени частное:

Решение:

Задание 18. Представьте в виде степени частное и найдите значение получившейся степени при x = 3 и n = 2

Решение:

Задание 19. Представьте в виде степени частное:

Решение:

Задание 20. Сократите дробь на c¹

Решение:

Задание 21. Представьте в виде степени следующее произведение:

Решение:

Задание 22. Представьте в виде степени следующее произведение:

Решение:

Задание 23. Представьте в виде степени следующее произведение:

Решение:

Задание 24. Представьте в виде степени следующее произведение:

Решение:

Задание 25. Представьте в виде степени следующее произведение:

Решение:

Задание 26. Представьте следующую степень в виде произведения степеней:

Решение:

Задание 27. Представьте следующую степень в виде произведения степеней:

Решение:

Задание 28. Представьте следующую степень в виде произведения степеней:

Решение:

Задание 29. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:

Решение:

Задание 30. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:

Решение:

Задание 31. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:

Решение:

Задание 32. Представьте в виде степени следующее выражение:

Решение:

Задание 33. Представьте в виде степени следующее выражение:

Решение:

Задание 34. Представьте в виде степени следующее выражение:

Решение:

Задание 35. Представьте в виде степени следующее выражение:

Решение:

Задание 36. Представьте в виде степени следующее выражение:

Решение:

Задание 37. Представьте в виде степени следующее выражение:

Решение:

Задание 38. Найдите значение следующего выражения:

Решение:

Задание 39. Найдите значение следующего выражения:

Решение:

Задание 40. Найдите значение следующего выражения:

Решение:

Задание 41. Найдите значение следующего выражения:

Решение:

Задание 42. Найдите значение следующего выражения:

Решение:

Задание 43. Найдите значение следующего выражения:

Решение:

Задание 44. Найдите значение следующего выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Степень и ее свойства (ЕГЭ — 2021)

Продолжим расширять круг чисел, «пригодных» в качестве показателя степени.{0}}=1\)

Свойства показателей степени с примерами: умножение, деление

Степень aⁿ равняется произведению числа a на само себя n-ое количество раз.

aⁿ = a * a * a… a (n раз)

В данном случае a – это основание, а n – показатель степени.

Примеры:

3¹ = 3
3² = 3 × 3 = 9
3³ = 3 × 3 × 3 = 27
3⁴ = 3 × 3 × 3 × 3 = 81
3⁵ = 3 × 3 × 3 × 3 × 3 = 243

Произошение:

Число a² следует произносить как “a в квадрате”. Например, 4² – это “четыре в квадрате”.
Число a³ произносится как “a в кубе”. Например, 4³ – это “четыре в кубе”.
Во всех остальных случаях aⁿ говорится как “a в n-ой степени”. Например, 4⁶ – это “четыре в шестой степени”.

Правила операций с показателями степени

#1. Умножение степеней (одинаковые основания)

aⁿ ⋅ a^m = a^n+m

Пример: 2² ⋅ 2³ = 2²⁺³ = 2⁵ = 32

#2. Степень произведения

(a ⋅ b)ⁿ = aⁿ ⋅ bⁿ

Пример: (2 ⋅ 3)⁴ = 2⁴ ⋅ 3⁴ = 1296

#3. Деление степеней (одинаковые основания)

aⁿ / a^m = a^n-m

Пример: 2⁵ ⋅ 2³ = 2^5-3 = 2² = 4

#4. Степень частного

(a / b)ⁿ = aⁿ / bⁿ

Пример: (12 / 4)³ = 12³ / 4³ = 27

#5. Возведение степени в степень

(aⁿ)^m = a^{n · m}

Пример: (5²)³ = 5^{2 · 3} = 3125

#6. Степень, возведенная в степень

a^{n^m} = a^{(n^m)}

Пример: 2^4² = 2^(4²) = 2^{(4 · 4)} = 2⁽¹⁶⁾ = 65536

#7. Извлечение степени из числа в степени

^m√(aⁿ) = aⁿ^/m

Пример: ³√(2⁶) = 2^6/3 = 2² = 2⋅2 = 4

#8. Возведение в отрицательную степень

b^-n = 1 / bⁿ

Пример: 2^-4 = 1 / 2⁴ = 1 / (2⋅2⋅2⋅2) = 1/16 = 0,0625

#9. Число в нулевой степени

a⁰ = 1

Пример: 10⁰ = 1

#10. Возведение нуля в степень

0ⁿ = 0, для n>0

Пример: 0⁷ = 0

#11. Число в первой степени

a¹ = a

Пример: 15¹ = 15

#12. Единица в степени (любой)

1ⁿ = 1

Пример: 1²⁰ = 1

#13. Минус один в степени

(-1)ⁿ = 1, если n – четное число

(-1)ⁿ = -1, если n – нечетное число

Пример: (-1)⁶ = 1

#14. Возведение числа в дробную степень (в числителе – единица)

a^1/n = ⁿ√a

Пример: 27^1/3 = ³√27 = 3

Смотрите также:

Три правила экспонент — Полный курс алгебры

Урок 13, Раздел 2

Вернуться в раздел 1

Правило 1. То же основание

Правило 2. Мощность продукта

Правило 3. Мощность мощности

Правило 1. То же основание

«Чтобы умножить степени одного основания, сложите экспоненты».

Например, a ² a ³ = a ⁵.

Почему мы добавляем экспоненты? Из-за того, что означают символы. Раздел 1.

Пример 1. Умножение 3 x ² · 4 x ⁵ · 2 x

Решение . Задача означает (Урок 5): умножьте числа, затем сложите степени x :

3 x ² · 4 x ⁵ · 2 x = 24 x ⁸

Два фактора x — x ² — умножить на пять факторов x — x ⁵ — умножить на один фактор x , произвести всего 2 + 5 + 1 = 8 множителей x : x ⁸.

Задача 1. Умножить. Примените правило Same Base.

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!

а)	5 x ² · 6 x ⁴ = 30 x ⁶	б)	7 x ³ · 8 x ⁶ = 56 x ⁹

в)	x · 5 x ⁴ = 5 x ⁵	г)	2 x · 3 x · 4 x = 24 x ³

e)	x ³ · 3 x ² · 5 x = 15 x ⁶	е)	x ⁵ · 6 x ⁸ y ² = 6 x ¹³ y ²

г)	4 x · y · 5 x ² · y ³ = 20 x ³ y ⁴	ч)	2 x y · 9 x ³ y ⁵ = 18 x ⁴ y ⁶

i)	a ² b ³ a ³ b ⁴ = a ⁵ b ⁷	к)	a ² bc ³ b ² ac = a ³ b ³ c ⁴

к)	x ^м y ⁿ x ^p y ^q = x ^{m + p} y ^{n + q}	л)	a ^p b ^q ab = a ^{p + 1} b ^{q + 1}

Проблема 2.Различают следующие:

x · x и x + x .

x · x = x ². x + x = 2 x .

Пример 2. Сравните следующее:

а) x · x ⁵ б) 2 · 2 ⁵

Решение .

а) x · x ⁵ = x ⁶

б) 2 · 2 ⁵ = 2 ⁶

Часть b) имеет ту же форму , что и часть a). Это часть а) с x = 2.

Один коэффициент на 2 умножает на пять коэффициентов на 2, получая шесть факторов на 2.

2 · 2 = 4 здесь неверно.

Проблема 3. Примените правило Same Base.

а)	x x ⁷ = x ⁸	б)	3 · 3 ⁷ = 3 ⁸	в)	2 · 2 ⁴ · 2 ⁵ = 2 ¹⁰

г)	10 · 10 ⁵ = 10 ⁶	д)	3 x · 3 ⁶ x ⁶ = 3 ⁷ x ⁷

Проблема 4.Примените правило Same Base.

а)	x ⁿ x ² = x ^{n + 2}	б)	x ⁿ x = x ^{n + 1}

в)	x ⁿ x ⁿ = x ^{2 n}	г)	x ⁿ x ^{1 — n} = x

e)	x · 2 x ^{n — 1} = 2 x ⁿ	е)	x ⁿ x ^м = x ^{n + m}

г)	x ^{2 n} x ^{2 — n} = x ^{n + 2}

Правило 2: Сила произведения факторов

«Увеличьте каждый коэффициент до той же степени.«

Например, ( ab ) ³ = a ³ b ³.

Почему мы можем это сделать? Опять же, согласно значению символов:

( ab ) ³ = ab · ab · ab = aaabbb = a ³ b ³.

Порядок факторов не имеет значения:

ab · ab · ab = aaabbb .

Задача 5. Применить правила экспонент.

а)

( x y ) ⁴ = x ⁴ y ⁴

б)

( pqr ) ⁵ = p ⁵ q ⁵ r ⁵

в)

(2 abc ) ³ = 2 ³ a ³ b ³ c ³

d) x ³ y ² z ⁴ ( xyz ) ⁵	=	x ³ y ² z ⁴ · x ⁵ y ⁵ z ⁵ Правило 2.

	=	x ⁸ y ⁷ z ⁹ То же основание.

Правило 3: Степень мощности

«Чтобы взять степень степени, умножьте экспонент».

Например, ( a ²) ³ = a ^{2 · 3} = a ⁶.

Почему мы это делаем? Опять же, из-за того, что означают символы:

( a ²) ³ = a ² a ² a ² = a ^{3 · 2} = a ⁶

Задача 6. Примените правила экспонент.

а)

( x ²) ⁵ = x ¹⁰

б)

( a ⁴) ⁸ = a ³²

в)

(10 ⁷) ⁹ = 10 ⁶³

Пример 3.Примените правила экспонент: (2 x ³ y ⁴) ⁵

Решение . В скобках указаны три множителя: 2, x ³ и y ⁴. Согласно Правилу 2 мы должны брать пятую степень каждого из них. Но чтобы взять степень степени, мы умножаем показатели. Следовательно,

(2 x ³ y ⁴) ⁵ = 2 ⁵ x ¹⁵ y ²⁰

Проблема 7.Применяйте правила экспонент.

а)	(10 a ³) ⁴ = 10 000 a ¹²	б)	(3 x ⁶) ² = 9 x ¹²

в)	(2 a ² b ³) ⁵ = 32 a ¹⁰ b ¹⁵	г)	( xy ³ z ⁵) ² = x ² y ⁶ z ¹⁰

e)	(5 x ² y ⁴) ³ = 125 x ⁶ y ¹²	е)	(2 a ⁴ до н.э. ⁸) ⁶ = 64 a ²⁴ b ⁶ c ⁴⁸

Проблема 8.Применяйте правила экспонент.

a) 2 x ⁵ y ⁴ (2 x ³ y ⁶) ⁵ = 2 x ⁵ y ⁴ · 2 ⁵ x ¹⁵ y ³⁰ = 2 ⁶ x ²⁰ y ³⁴

b) abc ⁹ ( a ² b ³ c ⁴) ⁸
= abc ⁹ · a ¹⁶ b ²⁴ c ³² = a ¹⁷ b ²⁵ c ⁴¹

Проблема 9.Используйте правила экспонент, чтобы вычислить следующее.

а) (2 · 10) ⁴ = 2 ⁴ · 10 ⁴ = 16 · 10 000 = 160 000

б) (4 · 10 ²) ³
= 4 ³ · 10 ⁶ = 64 000 000

в) (9 · 10 ⁴) ²
= 81 · 10 ⁸ = 8 100 000 000

В степенях 10 столько же нулей, сколько в экспоненте 10.

Пример 4. Квадрат x ⁴.

Решение . ( x ⁴) ² = x ⁸.

Чтобы возвести в квадрат степень, удвойте экспоненту.

Проблема 10. Возведите следующее.

а)	x ⁵ = x ¹⁰	б)	8 a ³ b ⁶ = 64 a ⁶ b ¹²

в)	−6 x ⁷ = 36 x ¹⁴	г)	x ⁿ = x ^{2 n}

Часть c) иллюстрации: Квадрат числа никогда не бывает отрицательным.

(−6) (- 6) = +36. Правило знаков.

Задача 11. Примените правило экспонент — если возможно.

а)

x ² x ⁵ = x ⁷, Правило 1.

б)

( x ²) ⁵ = x ¹⁰, Правило 3.

в)	x ² + x ⁵
	Невозможно. Правила экспонент применяют только к умножению.

В итоге: Добавьте экспонент, когда одно и то же основание появляется дважды: x ² x ⁴ = x ⁶. Умножьте экспоненты, когда основание появится один раз — и в скобках:
( x ²) ⁵ = x ¹⁰.

Задача 12. Примените правила экспонент.

а)

( x ⁿ) ⁿ = x ⁿ · ⁿ = x ^{n ²}

б)

( x ⁿ) ² = x ² ⁿ

Проблема 13.Примените правило экспонент или добавьте похожие термины — если возможно.

а) 2 x ² + 3 x ⁴
Невозможно. Это не похоже на термины .

б) 2 x ² · 3 x ⁴ = 6 x ⁶. Правило 1.

в) 2 x ³ + 3 x ³
= 5 x ³.Как термины. Показатель степени не меняется.

г) x ² + y ²
Невозможно. Это не термины.

д) x ² + x ²
= 2 x ². Как термины.

е) x ² · x ²
= x ⁴. Правило 1

г) x ² · y ³
Невозможно.Разные базы.

ч) 2 · 2 ⁶
= 2 ⁷. Правило 1

i) 3 ⁵ + 3 ⁵ + 3 ⁵ =
3 · 3 ⁵ (При добавлении подобных терминов) = 3 ⁶.

Мы продолжим правила экспонент в 21 уроке.

Следующий урок: Умножение. Распределительное правило.

Вернуться в раздел 1

Содержание | Дом

Вопросы или комментарии?

Электронная почта: themathpage @ яндекс.com

Гаджет Intel® Power

Загрузить

Intel® Power Gadget 3.5.9 для Windows *

Intel® Power Gadget 3.7.0 для MacOS *

Команда разработчиков

Windows *: Джо Оливас, Тимо Клеймола, Марк Прайс, Тимоти Маккей
MacOS *: Патрик Консор

Предыдущие участники

Windows * : Сеунг-Ву Ким, Картик Кришнан, Вардхан Дугар, Джозеф Джин-Сун Ли, Джун Де Вега

Введение

Intel® Power Gadget — это программный инструмент для мониторинга энергопотребления, доступный для процессоров Intel® Core ™ (от 2-го поколения до 10-го поколения Intel® Core ™).Процессоры Intel® Atom ™ не поддерживаются. Он поддерживается в Windows * и macOS * и включает приложение, драйвер и библиотеки для отслеживания и оценки в реальном времени информации о мощности пакета процессора в ваттах с использованием счетчиков энергии в процессоре. В этом выпуске мы предоставляем функциональные возможности для оценки информации о мощности на различных платформах, включая ноутбуки, настольные компьютеры и серверы. Windows 7 * и 32-разрядные версии Intel® Power Gadget для Windows * прекратили разработку с 3.0,7. Начиная с версии 3.5 и далее будут поддерживаться только 64-разрядная версия и Windows 8 *.

Фон

Традиционные методы оценки энергопотребления / мощности процессора всегда были сложной задачей, которая включала в себя специальные инструменты или приборы на платформе вместе с оборудованием сторонних производителей. Мотивация к созданию инструмента заключалась в том, чтобы помочь конечным пользователям, независимым поставщикам ПО, производителям оборудования, разработчикам и другим лицам, заинтересованным в более точной оценке мощности на уровне программного обеспечения без каких-либо аппаратных средств.

Новые функции

В версии 3.0 есть дополнительные функции, которые включают оценку мощности в многопроцессорных системах, а также внешние API-интерфейсы для извлечения информации о мощности в разделах кода. Поддержка нескольких разъемов по существу оценивает Energy MSR для каждого разъема и дает оценку потребляемой мощности на разъем. Уровень API — это набор вызываемых библиотек и dll, обеспечивающих гибкость для создания инструмента в разделах кода приложения.Последний выпуск также включает поддержку Windows 10 *.

**Краткое описание (Windows *)**

Intel® Power Gadget 3.5 состоит из следующих компонентов. Набор драйверов и библиотек, которые обращаются к счетчику энергии процессора и обрабатывают его для расчета энергопотребления в ваттах, умеренной температуры в градусах Цельсия и частоты в ГГц (каталог установки по умолчанию будет ~ Program FilesIntelPower Gadget 3.5). Версия инструмента для командной строки (PowerLog3.0.exe) также включена

**Системные требования (Windows *)**

Windows 8 *
Windows 10 *
Windows Server 2008, Windows Server 2012
Microsoft.NET * Framework 4
Распространяемый пакет Microsoft Visual C ++ 2017
Процессор Intel® Core ™ 2-го поколения или новее, более старые процессоры не поддерживаются
- Розетка одинарная
- Универсальная розетка

**Системные требования (MacOS *)**

macOS * 10.11 или новее
Процессор Intel® Core ™ 2-го поколения или новее

Известные ограничения / проблемы

Графики не появятся, если ваш процессор не имеет соответствующих аппаратных счетчиков
Дискретные видеокарты не поддерживаются, и графики графического процессора не отображаются, если не используется графика Intel
Поддерживаемые Windows 7 * сборки приведены ниже в разделе «Архив»

**Установка / настройка (Windows *)**

Запустите пакет msi от имени администратора.Принять UAC, если появится
Следуйте инструкциям установщика для завершения установки.
1. .Net Framework 4 (будет автоматически загружен с сайта Microsoft *, если еще не установлен в вашей системе) требует подключения к Интернету
2. Распространяемый пакет Microsoft * Visual C ++ 2017 (устанавливается автоматически, если еще не установлен)

**Установка / настройка (macOS *)**

Дважды щелкните загруженный DMG (Intel Power Gadget.dmg)
Дважды щелкните пакет (Установить Intel Power Gadget.pkg)
Следуйте инструкциям установщика для завершения установки

В последних версиях macOS после установки пользователям необходимо явно разрешить загрузку драйвера Power Gadget:

Откройте «Системные настройки» и нажмите «Безопасность и конфиденциальность».
Нажмите на замок внизу страницы, чтобы разблокировать изменения.
Нажмите «Разрешить», чтобы разрешить системное программное обеспечение от Intel Corporation:
Перезагрузите компьютер, чтобы изменения вступили в силу

В macOS Catalina (10.15), пользователям может потребоваться выполнить дополнительные действия, чтобы включить автоматическую загрузку драйвера Power Gadget (это связано с ошибкой в macOS).

Открыть приложение Терминал
Введите следующую команду и нажмите Enter (для завершения требуется пароль):
1. ```
  sudo touch / Библиотека / Расширения  
```
Перезагрузите компьютер, чтобы изменения вступили в силу

**Использование (Windows *)**

Гаджет Intel® Power Gadget обычно используется для отслеживания энергопотребления процессора.

Показывает мощность процессора (Вт), температуру (Цельсия) и частоту (МГц) в реальном времени с помощью графика, отображаемого в графическом интерфейсе пользователя
Позволяет регистрировать измерения мощности и частоты и сохранять их в формате csv.
Дважды щелкните ярлык на рабочем столе, и графический интерфейс запустит
Перетащите, чтобы переместить графический интерфейс.
Щелкните правой кнопкой мыши графический интерфейс, и появится всплывающее меню, позволяющее выбрать параметры или закрыть приложение. Опции имеют следующие параметры. Нажмите кнопку «Начать журнал» в графическом интерфейсе пользователя, чтобы начать регистрацию. Нажмите ту же кнопку «Остановить журнал», чтобы остановить запись. Во время записи в области диаграммы мощности будет мигать красная метка «REC».
Вы можете добавить отметку времени к имени файла журнала или нет.
Вы можете выбрать имя файла журнала.
Вы можете изменить размер графического интерфейса от 100% до 300%, перетащив ползунок и протестировав новый размер с помощью кнопки «Применить размер», а затем принять изменения, нажав «ОК».
Разрешение обновления экрана позволяет вам изменить частоту обновления графического интерфейса пользователя во время выполнения. Это может быть от 50 до 1000 мс. (По умолчанию установлено 1000 мс)
Разрешение выборки журнала позволяет изменять разрешение выборки журнала в диапазоне от 1 мс до 1000 мс.(По умолчанию 100 мс)
В системе с несколькими сокетами вы можете выбрать, какую информацию о пакете отображать в графическом интерфейсе. Журнал будет записывать всю информацию о пакете в файл csv.
Нажмите кнопку «Начать журнал» в графическом интерфейсе пользователя, чтобы начать регистрацию. Нажмите ту же кнопку «Остановить журнал», чтобы остановить запись. Во время регистрации красная метка «REC» будет мигать в области диаграммы мощности

Использование Intel® Power Gadget 3.0 в скрипте

Чтобы запустить и остановить регистрацию в сценарии, сначала запустите графический интерфейс как обычно.

В начале сценария вызовите «IntelPowerGadget.exe -start», и он запустит регистрацию в графическом интерфейсе.
В конце сценария вызовите «IntelPowerGadget.exe -stop», и он остановит ведение журнала.

Параметры журнала основаны на параметрах, установленных в графическом интерфейсе пользователя.

PowerLog3.0

PowerLog3.0.exe — это версия командной строки Intel® Power Gadget для регистрации энергопотребления

использование:

Записывать данные о питании в файл журнала за период времени:

  PowerLog3.0.exe [-resolution ] –duration  [-verbose] [-file ]

Запустить команду и записать данные о мощности в файл журнала до завершения команды:

  PowerLog3.0.exe [-разрешение <мсек>] [-файл <файл журнала>] [-verbose] -cmd <команда>

Данные файла журнала

Файл журнала будет включать истекшее время, предел мощности пакета, частоту процессора, частоту GT, температуру процессора, среднюю и совокупную мощность процессора

Энергия процессора (общая энергия процессора) = IA Energy + GT Energy (если применимо) + Другое (не измеряется)
IA Energy (Энергия ЦП / ядер процессора)
GT Energy (Энергия графической подсистемы процессора) — если применимо, некоторые процессоры для настольных компьютеров и серверов ее не имеют или могут использовать дискретную графику.

Работает только с процессорами Intel® Core ™ 2-го поколения или новее.Процессоры Atom пока не поддерживаются.

Использовать только 32-разрядный установщик для 32-разрядной ОС и 64-разрядный установщик для 64-разрядной ОС

Приложение может зависать после долгой работы (просто закройте и перезапустите приложение)

Обратитесь в местное торговое представительство Intel или к своему дистрибьютору, чтобы получить последние спецификации и перед размещением заказа на продукцию.

В этом документе содержится информация о продуктах, находящихся на стадии проектирования.

Все продукты, платформы, даты и цифры являются предварительными, основанными на текущих ожиданиях, и могут быть изменены без предварительного уведомления.Все указанные даты являются плановыми, предназначены только для целей планирования и могут быть изменены.

В этом документе содержится информация о продуктах, находящихся на стадии проектирования. Не завершайте дизайн этой информацией. Обновленная информация будет опубликована, когда продукт станет доступен. Перед окончательной доработкой дизайна уточните в местном офисе продаж, что у вас есть последняя версия таблицы.

Приведенные кодовые названия используются внутри корпорации Intel для обозначения продуктов, которые находятся в разработке и еще не объявлены публично о выпуске.Клиенты, лицензиаты и другие третьи стороны не уполномочены Intel использовать кодовые имена в рекламе, продвижении или маркетинге каких-либо продуктов или услуг, и любое такое использование внутренних кодовых имен Intel является исключительным риском пользователя.

Intel и логотип Intel являются товарными знаками корпорации Intel в США и других странах.

* Другие названия и бренды могут быть заявлены как собственность других лиц.

Intel® Power Gadget также предоставляет интерфейс прикладного программирования (API) C / C ++ для доступа к этим данным мощности и частоты в вашей программе; API поддерживается в Windows и Mac OS X. Для получения дополнительной информации об API см .:

для Mac с использованием Intel® Power Gadget API в Mac OS X

для Windows с использованием Intel® Power Gadget API в Windows

Лицензионное соглашение

с конечным пользователем, включенное в Windows * скачать

Уведомления

ИНФОРМАЦИЯ В ДАННОМ ДОКУМЕНТЕ ПРЕДОСТАВЛЯЕТСЯ В СВЯЗИ С ПРОДУКТАМИ INTEL®.ДАННЫЙ ДОКУМЕНТ НЕ ПРЕДОСТАВЛЯЕТ НИКАКИХ ПРАВ НА ИНТЕЛЛЕКТУАЛЬНУЮ СОБСТВЕННОСТЬ, ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ, ОТ ESTOPPEL ИЛИ Иным образом. ЗА ИСКЛЮЧЕНИЕМ УСЛОВИЙ ПРОДАЖИ ТАКИХ ПРОДУКТОВ INTEL, INTEL НЕ НЕСЕТ НИКАКОЙ ОТВЕТСТВЕННОСТИ И ОТКАЗЫВАЕТСЯ ОТ ЛЮБЫХ ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ В ОТНОШЕНИИ ПРОДАЖИ И / ИЛИ ИСПОЛЬЗОВАНИЯ ГАРАНТИЙНЫХ ПРОДУКТОВ, ВКЛЮЧАЯ ОТВЕТСТВЕННОСТЬ ПО ОТВЕТСТВЕННОСТИ , КОММЕРЧЕСКОЙ ЦЕННОСТИ ИЛИ НАРУШЕНИЯ ЛЮБОГО ПАТЕНТА, АВТОРСКОГО ПРАВА ИЛИ ДРУГОГО ПРАВА НА ИНТЕЛЛЕКТУАЛЬНУЮ СОБСТВЕННОСТЬ.

, ЕСЛИ ПРОДУКТЫ INTEL НЕ РАЗРАБОТАНЫ И НЕ ПРЕДНАЗНАЧЕНЫ ДЛЯ КАКИХ-ЛИБО ПРИЛОЖЕНИЙ, В КОТОРЫХ НЕИСПРАВНОСТЬ ПРОДУКТА INTEL МОЖЕТ СОЗДАТЬ СИТУАЦИЮ, КОТОРАЯ МОЖЕТ СОЗДАТЬ СИТУАЦИЮ, КОТОРАЯ МОЖЕТ ПРИВЕСТИ К ТРАВМЕ ИЛИ СМЕРТИ.

Intel может вносить изменения в спецификации и описания продуктов в любое время без предварительного уведомления. Разработчики не должны полагаться на отсутствие или характеристики каких-либо функций или инструкций, помеченных как «зарезервировано» или «не определено». Intel резервирует их для будущего определения и не несет никакой ответственности за конфликты или несовместимость, возникающие в результате будущих изменений в них.Информация здесь может быть изменена без предварительного уведомления. Не завершайте дизайн этой информацией.

Продукты, описанные в этом документе, могут содержать конструктивные дефекты или ошибки, известные как исправления, которые могут привести к отклонению продукта от опубликованных спецификаций. Текущие исправления доступны по запросу.

Обзор

Nvidia GeForce RTX 3090 Founders Edition: наследник престола титанов

GeForce RTX 3090 Founders Edition: абсолютная единица

Nvidia GeForce RTX 3090 Founders Edition теперь занимает первое место в нашей иерархии тестов GPU , хотя где она попадает в лучших видеокарт , ответить на этот вопрос сложнее .В то время как GeForce RTX 3080 сохранила существующую ценовую структуру серии RTX 20, заменив RTX 2080 Super по цене 699 долларов, RTX 3090 видит стартовую цену RTX 2080 Ti в размере 1200 долларов и повышает ее еще на одну. 300 долларов. Однако есть и альтернативная точка зрения: GeForce RTX 3090 также является заменой Titan RTX за 2500 долларов, и в этом случае это более быстрая карта, которая стоит на 1000 долларов меньше. В любом случае вам понадобятся несколько глубоких карманов, если вы хотите владеть новой гало-картой Nvidia.

У нас уже есть подробное описание архитектуры Ampere , в которой подробно рассказывается о том, что делает GeForce RTX 3090 отличной. Начните с этого, если вам нужна дополнительная информация о , как , 3090 и GA102 обеспечивают новый уровень производительности. Мы рассмотрим основные моменты здесь, но простой ответ заключается в том, что Nvidia пошла с меньшим технологическим узлом, большим количеством ядер, более быстрой памятью … плюс больше мощности и более высокой цене. При 350 Вт TGP (общая графическая мощность) это, безусловно, самый энергоемкий потребительский графический процессор, который Nvidia когда-либо выпускала (не считая двух GPU).Это также самый дорогой графический процессор под маркой GeForce из когда-либо существовавших (если не считать двухъядерный GeForce GTX Titan Z, чего я не считаю).

У нас есть несколько дополнительных тестов, которые мы все еще пытаемся провести, прежде чем мы вынесем окончательный вердикт (глядя на вас 8K, или, по крайней мере, 4K с DSR, имитирующим 8K), так что окончательного вердикта у нас пока нет. У нас также есть несколько карточек партнеров AIB (дополнительная плата), которые мы рассмотрим в ближайшие дни, когда у нас будет время провести все тесты и собрать некоторые данные.

Одна вещь, которую мы не можем полностью предсказать, — это доступность, но мы догадываемся, что она не будет хорошей.На самом деле это больше, чем догадка, поскольку Nvidia вчера заранее извинилась перед за ограниченную доступность карт RTX 3090 (в то же время подтвердив ожидания производительности). Тьфу. Учитывая, что карты RTX 3080 распродаются так же быстро, как и складские запасы, даже несмотря на то, что RTX 3090 стоит вдвое дороже … ну, некоторые люди платят почти 1500 долларов за карты RTX 3080. Вероятно, будет неприятно, если вы настроились на 3090 и не сделали предварительный заказ.Просто дайте ему немного времени, и со временем все должно уладиться. Реплика мамы: «Терпение — добродетель!» Спасибо, мама, но я все еще работаю над этим.

Краткое описание GeForce RTX 3090 вполне соответствует вашим ожиданиям. Теоретически это примерно на 20% быстрее, чем RTX 3080, исходя только из технических характеристик, с более чем вдвое большим объемом памяти. Дополнительная видеопамять не имеет большого значения для большинства игр, если вы не используете 8 КБ (может быть, 5 КБ), но она может оказаться полезной для некоторых профессиональных рабочих нагрузок. RTX 3090 также требует мощного процессора, чтобы получить максимальную отдачу от карты (в ближайшие дни мы проведем несколько дополнительных тестов, чтобы показать это, но вы можете получить некоторое представление о том, чего ожидать от масштабирования нашего процессора RTX 3080. статья ).Это в значительной степени графический процессор, разработанный для игр 4K Ultra, и при этих настройках он в среднем на 12% быстрее, чем 3080 в нашем существующем наборе тестов, и на 14% быстрее в нашем наборе бонусных тестов. Снизьте до 1440p ultra, и 3090 будет всего на 8% быстрее, чем 3080. Если вы используете 1080p? Не беспокойтесь, серьезно.

Теперь давайте углубимся в спецификации и посмотрим, что изменилось по сравнению с другими графическими процессорами Nvidia.

Характеристики графического процессора Nvidia

10112 72

2 9011 90112 9011 9011

901 9018 9018 9018 9018 9018 9018 9018 9018 9018

9011 901 9011 9011 901

FP18 9218

9011 9011 9011 9011 ^Вт)

1212 9011

$ 1,4183 2499 долл. США

Графическая карта	RTX 3090 FE	RTX 3080 FE	Titan RTX	RTX 2080 Ti FE
Архитектура	GA102	9011 9011 9011 GA102	9011 TG102 9011 9011 9011 9011 G102 9011 TG Технологии	Samsung 8N	Samsung 8N	TSMC 12FFN	TSMC 12FFN
Транзисторы (миллиард)	28.2)	628,4	628,4	754	754
SMs	82	68	68
4352
Ядра графического процессора (INT32)	5248	4352	4608	4352
Тензорные ядра	328	272	68	72	68
Базовая частота (МГц)	1395	1440	1350	1515
Тактовая частота с ускорением (МГц) 011 903 901 9011 9011 901 903 903 1635
Скорость видеопамяти (Гбит / с)	19.5	19	14	14
VRAM (GB)	24	10	24	11
Ширина шины VRAM	383 320
ROP	112	96	96	88
TMU	328	272	288	272
29,8	16,3	14,2
TOPS INT32	17,8	14,9	16,3	14,2
Tensor Tensor TFLO12 (Sparsity) 14,2	130	114
RT TFLOPS	69,5	58,1	49,2	45,7
Полоса пропускания (ГБ / с)	93612	350	320	285	260
Дата выпуска	Сентябрь 2020	Сентябрь 2020	Декабрь 2018	Сентябрь 2018
1,199 долл. США

Архитектура GeForce RTX 3090: почти полная GA102

(Изображение предоставлено Tom’s Hardware)

И снова наша архитектура Ampere более подробно описывает различные аспекты новых графических процессоров 30-й серии.Есть много изменений по сравнению с предыдущей архитектурой Turing , но вот основные моменты.

Во-первых, GA102 использует техпроцесс Samsung 8N, что означает больше транзисторов на меньшей площади, чем TU102. Если смотреть строго на общую плотность транзисторов, GA102 содержит 45 миллионов транзисторов на квадратный миллиметр, тогда как плотность TU102 составляет «всего» 24,7 миллиона транзисторов на квадратный миллиметр. Это хорошо, но явно не так хорошо, как узел TSMC N7: более крупный чип GA100, используемый в A100 от Nvidia, содержит 65.4 миллиона транзисторов на квадратный миллиметр. Кроме того, AMD Navi 10 имеет 41 миллион транзисторов на квадратный мм, так что Nvidia, по крайней мере, соответствует этому уровню плотности — хотя сравнение архитектур определенно смотрит на яблоки и апельсины.

Далее, GeForce RTX 3090 использует почти полный чип GA102. Из 84 потенциальных SM (потоковых мультипроцессоров) только два отключены. Это говорит о том, что либо доходность очень хорошая… либо Nvidia не планирует продавать почти столько же 3090 чипов, сколько 3080 чипов.Мы подозреваем, что второй вариант ближе к истине, а фактическая доходность в наши дни строго охраняется. 3090 также имеет семь GPC (кластеров обработки графики), а ROP (выходные данные рендеринга) теперь являются частью GPC вместо контроллера памяти, что дает 3090 112 ROPS.

Возможно, большее изменение состоит в том, что GeForce RTX 3090 оснащена 24 ГБ памяти GDDR6X, на этот раз с тактовой частотой 19,5 Гбит / с (по сравнению с 19 Гбит / с на 3080). Это достигается включением двух последних 32-битных контроллеров памяти на GA102, а затем запуском 24 микросхем в режиме 16-битного интерфейса половинной ширины.Это также означает, что чипы GDDR6X расположены с обеих сторон печатной платы (печатной платы), тогда как RTX 3080 имеет память только на той же стороне, что и графический процессор. Конечно, возникает вопрос, насколько это влияет на температуру памяти GDDR6X , особенно когда половина VRAM не охлаждается активно. Однако в настоящее время у нас нет возможности измерить температуру чипа GDDR6X.

(Изображение предоставлено Tom’s Hardware)

Мы довольно много обсуждали изменения ядра CUDA графического процессора в предыдущих статьях Ampere, потому что это одно из самых значительных различий между Ampere и Turing.Тьюринг включил 64 ядра CUDA с поддержкой FP32 на каждый SM, с дополнительными 64 ядрами CUDA с поддержкой INT32 (и два ядра FP64 для целей совместимости). Ядра FP32 и INT32 были отдельными путями данных и могли использоваться одновременно. Ядра FP32 также могут выполнять математические вычисления FP16 с удвоенной производительностью — в режиме «быстрой математики».

Для Ampere ядра FP32 теряют поддержку быстрой математики FP16, которая переносится на ядра Tensor — это по-прежнему вдвое выше производительности FP16 по сравнению с выделенными ядрами FP32, но в целом равна производительности FP16.Между тем, ядра INT32 получают поддержку вычислений FP32, что означает, что общая производительность FP32 на SM удвоилась. В то же время производительность INT32 на SM осталась прежней. Это имеет некоторые интересные последствия для общей производительности, но в основном около 30-35% рабочей нагрузки ядра CUDA в играх составляет INT32 (для поиска указателя адреса, вычисления текстур и другой подобной работы). Это означает, что значительная часть второго канала данных будет занята INT32, поэтому реальный прирост производительности часто будет меньше, чем можно было бы предположить по исходному количеству TFLOPS FP32.

В другом месте тензорные ядра — еще одно существенное обновление по сравнению с Turing, с удвоенной пропускной способностью на ядро. Только вот тензорных ядер на SM вдвое меньше. Тензорные ядра 3-го поколения действительно добавляют поддержку мелкозернистой разреженности, которая при использовании может снова удвоить пропускную способность по сравнению с Turing. Также стоит отметить, что тензорные ядра 3-го поколения добавляют поддержку типов данных INT8 и INT4 в 2 и 4 раза большей базовой пропускной способности FP16.

(Изображение предоставлено Tom’s Hardware)

Видеопорты на GeForce RTX 3090 FE такие же, как на RTX 3080: один HDMI 2.1 порт и три выхода DisplayPort 1.4a. В этом раунде нет порта VirtualLink, так как VirtualLink в основном мертв . Все четыре выхода поддерживают 8K60 с использованием DSC (Display Stream Compression), техники «без визуальных потерь», которая на самом деле не является визуально без потерь (хотя вы, вероятно, не заметите на 8K). Мы видели другие карты с пятью выходами на дисплей, многие из которых выбрали двойной HDMI 2.1, так что имейте это в виду, если вы планируете использовать настройку с несколькими мониторами.

Другие изменения (и мы тут кое-что замалчиваем, поскольку мы уже рассмотрели это в обзоре RTX 3080, а также в части архитектуры Ampere) включают ядра RT, которые в два раза быстрее — или даже больше в некоторых рабочие нагрузки (например, размытие в движении).Емкость и пропускная способность кэша L1 / общей памяти были увеличены. Кэш L2 также больше, чем раньше, и кэш L1 может быть настроен как различное количество L1 по сравнению с общей памятью, в зависимости от потребностей приложения. Размер файла регистров также увеличивается, и GA102 может одновременно выполнять RT + графику + DLSS (ранее использование ядер RT остановило бы ядра CUDA).

Операторы растра (ROPS) были перемещены из контроллеров памяти в GPC. Каждый GPC имеет две секции ROP по восемь блоков ROP в каждой.Это обеспечивает большую гибкость в работе, давая GA102 и RTX 3090 в общей сложности 112 ROPS. Каждый GPC также включает шесть TPC (кластеров обработки текстур) с восемью TMU (блоки отображения текстур) и механизм полиморфизма, хотя они идут парами, и Nvidia позволяет использовать 41 TPC для 3090.

Наконец, как обсуждалось ранее, память RTX 3090 В контроллере появилась новая функция под названием EDR: обнаружение и воспроизведение ошибок. Когда память обнаруживает неудачную передачу, а не сбой или повреждение данных, она просто пытается снова.Он будет пытаться делать это до тех пор, пока не добьется успеха, хотя все еще возможно вызвать сбой при разгоне памяти. EDR допускает возможность более высоких тактовых частот памяти, которые на самом деле могут не работать лучше по мере приближения к пределам памяти. Это связано с тем, что EDR приводит к снижению общей пропускной способности памяти при сбое передачи.

GeForce RTX 3090 Founders Edition: дизайн, охлаждение, эстетика

Изображение 1 из 6

(Изображение предоставлено: Tom’s Hardware) Изображение 2 из 6

(Изображение предоставлено: Tom’s Hardware) Изображение 3 из 6

(Изображение предоставлено: Tom’s Hardware) Изображение 4 из 6

(Изображение предоставлено: Tom’s Hardware) Изображение 5 из 6

(Изображение предоставлено: Tom’s Hardware) Изображение 6 из 6

(Изображение предоставлено: Tom’s Hardware)

Nvidia внесла значительные изменения в своих основателей Карты Edition для RTX 30-й серии.Новые конструкции по-прежнему включают в себя два осевых вентилятора, но Nvidia сильно изменила дизайн печатной платы и укоротила ее, так что « задняя часть » карты (вдали от видеопортов) состоит только из вентилятора, тепловых трубок, ребер радиатора и обычной видеокарты. пелена. Nvidia заявляет, что новый дизайн обеспечивает существенное повышение эффективности охлаждения, в то же время снижая уровень шума. GeForce RTX 3090 FE отражает общий промышленный дизайн и эстетику 3080 FE, а затем нажимает кнопку Get Pumped.

GeForce RTX 3090 Founders Edition огромна, и мы имеем в виду это буквально. Его вес составляет 2189 г, или 4,82 фунта. Возможно, это не самая тяжелая карта с одним графическим процессором из когда-либо созданных, но с трехслотовым кулером это определенно самая большая карта, созданная Nvidia. 3090 FE также имеет длину 313 мм (12,3 дюйма), что примерно на 3 см длиннее, чем 3080 FE, и его высота 138 мм (5,43 дюйма). Это примерно на дюйм больше в каждом измерении, чем у его маленького брата, и он очень прочный — будущие археологи откопают их и, вероятно, подумают, что мы использовали их, чтобы дубинять друг друга.

Изображение 1 из 3

(Изображение предоставлено: Tom’s Hardware) Изображение 2 из 3

(Изображение предоставлено: Tom’s Hardware)

VSWR

Чтобы радиостанция (передатчик или приемник) подавала питание на антенну,
сопротивление радио и линии передачи должно быть хорошо согласовано с
сопротивление антенны.
Параметр VSWR является мерой, которая
численно описывает, насколько хорошо антенна согласована по импедансу с радио или линией передачи, к которой она подключена.

КСВН означает коэффициент стоячей волны напряжения , и также упоминается как коэффициент стоячей волны (КСВ).КСВН является функцией коэффициента отражения, который описывает мощность, отраженную от антенны.
Если коэффициент отражения равен
данный
, то КСВ определяется по следующей формуле:

Коэффициент отражения
также известен как s11 или возвратные потери. См. Таблицу vswr ниже, чтобы увидеть числовое сопоставление
между отраженной мощностью s11 и КСВН. Если вы не хотите проходить сложные уравнения, чтобы понять
взаимосвязь между VSWR, потерями рассогласования, s11 / gamma, и хотелось бы, чтобы калькулятор сделал это за вас, проверьте
наша страница калькулятора VSWR, и мы сделаем VSWR
конверсия для вас.

КСВН для антенн всегда является действительным положительным числом. Меньший
Чем больше КСВН, тем лучше антенна согласована с линией передачи и тем больше мощности передается на антенну.
Минимальный КСВ — 1,0. В этом случае мощность не отражается от антенны, что идеально.

Часто антенны должны удовлетворять требованиям к полосе пропускания, которые выражаются в КСВН. Например, антенна может
утверждают, что работают в диапазоне 100-200 МГц с КСВН

Физическое значение КСВН

КСВН определяется по напряжению, измеренному на линии передачи.
ведущий к антенне.КСВН — это отношение максимальной амплитуды стоячей волны к минимальной амплитуде.
стоячей волны, как показано на следующем рисунке:

Рисунок 1. Напряжение, измеренное вдоль линии передачи.

В промышленности КСВН иногда произносится как «viz-wer».

Когда антенна не согласована с приемником, мощность отражается (так что коэффициент отражения,,
не равно нулю). Это вызывает «отраженную волну напряжения», которая создает стоячие волны.
вдоль ЛЭП. Результатом являются пики и спады, как показано на
Фигура 1.Если VSWR = 1.0, не будет отраженной мощности и напряжение будет иметь постоянную величину.
вдоль ЛЭП.

КСВН, отраженная мощность и s11

КСВ = 3 — это плохо? Насколько плох КСВ, равный 12? Что ж, жестких правил нет. В этом разделе мы постараемся поставить
номер КСВН в контексте. Ниже приведена таблица, показывающая соотношение между КСВН, полной отраженной мощностью и
(также известный как s11) и полная отраженная мощность. Обратите внимание, что отраженная мощность просто
коэффициент отражения () в квадрате.Таблица I. КСВН, отраженная мощность и (s11)

КСВН	(s11)	Отраженная мощность (%)	Отраженная мощность (дБ)
1,0	0,000	0,00	-Бесконечность
1,5	0.200	4,0	-14,0
2,0	0,333	11,1	-9,55
2,5	0.429	18,4	-7,36
3,0	0,500	25,0	-6,00
3,5	0,556	30,9	-5,10
4,0	0,600	36,0	-4,44
5,0	0,667	44,0	-3,52
6,0	0,714	51.0	-2,92
7,0	0,750	56,3	-2,50
8,0	0,778	60,5	-2,18
9,0	0,800	64,0	-1,94
10,0	0,818	66,9	-1,74
15,0	0,875	76.6	-1,16
20,0	0,905	81,9	-0,87
50,0	0,961	92,3	-0,35

В приведенной выше таблице КСВ, равное 4, имеет 36% мощности, передаваемой приемником, отраженной от антенны (64% мощности передается
к антенне). Обратите внимание, что отраженная мощность 0 дБ означает, что вся мощность отражена (100%), тогда как -10 дБ означает 10% мощности.
сила отражена.Если вся мощность будет отражена, КСВ будет бесконечным.

Обратите внимание, что КСВН сильно нелинейная функция коэффициента отражения. То есть очень мало
разница в отраженной мощности при увеличении КСВН с 9 до 10; однако есть изменение отраженной мощности на 11%, когда КСВН
меняется с 1 на 2.

В целом, если КСВ меньше 2, согласование антенны считается очень хорошим и мало что дает.
согласованием импеданса. Увеличение КСВН имеет два основных недостатка.Первое очевидно: отражается больше мощности
от антенны и поэтому не передается. Однако возникает другая проблема. Чем больше КСВН, тем больше отражается мощность.
к радио, которое передает. Большое количество отраженной мощности может повредить радио. Кроме того, у радио есть проблемы
передача правильных информационных битов, когда антенна плохо согласована (это численно определяется в терминах другой метрики,
EVM — величина вектора ошибки).

Характеристики КСВ антенн

Часто в промышленности антенны экранируются (критерий годен / не годен) на основе характеристик КСВН (характеристик КСВН).Это
метод пассивного измерения антенн, чтобы быстро определить, правильно ли они настроены. Антенна
измеряется анализатором цепей, и записывается КСВН как функция частоты. В качестве примера рассмотрим
эта ситуация, когда КСВ 5 антенн измеряется и наносится на график вместе с 4 линиями, которые представляют КСВН
характеристики этой антенны (синего цвета):

Рисунок 2. График зависимости КСВН для 5 антенн от частоты.

Характеристики КСВН на рисунке 2 определены следующим образом:

(1) КСВН
(2) КСВ> 4.0 для 1200 МГц
(3) КСВН> 3,0 на частоте f = 1,7 ГГц, линейно сниженный до КСВН> 2,0 на частоте f = 1,8 ГГц

(4) КСВН

На рисунке 2 антенна с красной кривой КСВН не соответствует второй спецификации,
а светло-синяя антенна с кривой КСВН (незначительно) не соответствует четвертой спецификации.
Это показано на рисунке 3:

Рисунок 3. Характеристики КСВН и кривые КСВ.

Установка характеристик КСВН — довольно сложная задача для инженеров-антенн. Идея состоит в том, чтобы подвести выбросы (расстроенные
антенны или антенны со сломанными разъемами и т. д.).Однако на практике определить
какова допустимая дисперсия, особенно в крупносерийных отраслях, где жесткая спецификация может привести к провалу тысяч
хороших антенн.

Обратите внимание, что КСВН — это показатель мощности, подаваемой на антенну. Это не значит, что антенна излучает
вся власть, которую он получает. Следовательно, КСВН измеряет потенциал излучения . Низкий КСВН означает, что антенна хорошо согласована,
но это не обязательно означает, что передаваемая мощность также излучается.Безэховая камера или другой тест излучаемой антенны
требуется для определения излучаемой мощности. КСВН недостаточно, чтобы определить, что антенна работает правильно.

КСВН также можно измерить с помощью диаграммы Смита. VSWR
это всего лишь скалярное измерение, тогда как диаграмма Смита показывает и величину, и фазу.
См. Диаграмму Смита
страницу для более подробной информации.

Верх: VSWR

Определения антенн

Главная: Теория антенн.com (Дом)

Эта страница, посвященная VSWR (коэффициент стоячей волны напряжения), защищена авторским правом. Никакая часть не может быть воспроизведена без разрешения
от автора. Авторское право antenna-theory.com, 2009-2017, КСВН.

Двоично-десятичный преобразователь

Из
Двоичный Десятичный Шестнадцатеричный

Чтобы
Двоичный Десятичный Шестнадцатеричный

Преобразователь десятичной системы в двоичную ►

Как преобразовать двоичное в десятичное

Для двоичного числа с n цифрами:

д _н-1… d ₃ d ₂ d ₁ d ₀

Десятичное число равно сумме двоичных цифр (d _n), умноженной на их степень двойки (2 ⁿ):

десятичный = d ₀ × 2 ⁰ + d ₁ × 2 ¹ + d ₂ × 2 ² + …

Пример

Найдите десятичное значение для 111001 ₂:

двоичное число:	1	1	1	0	0	1
степень 2:	2 ⁵	2 ⁴	2 ³	2 ²	2 ¹	2 ⁰

111001 ₂ = 1⋅2 ⁵ + 1⋅2 ⁴ + 1⋅2 ³ + 0⋅2 ² + 0⋅2 ¹ + 1⋅2 ⁰ = 57 ₁₀

Таблица преобразования двоичных чисел в десятичные

Двоичный Число	Десятичное число Число	Hex Число
0	0	0
1	1	1
10	2	2
11	3	3
100	4	4
101	5	5
110	6	6
111	7	7
1000	8	8
1001	9	9
1010	10	A
1011	11	В
1100	12	С
1101	13	D
1110	14	E
1111	15	F
10000	16	10
10001	17	11
10010	18	12
10011	19	13
10100	20	14
10101	21	15
10110	22	16
10111	23	17
11000	24	18
11001	25	19
11010	26	1А
11011	27	1Б
11100	28	1С
11101	29	1D
11110	30	1E
11111	31	1 этаж
100000	32	20
1000000	64	40
10000000	128	80
100000000	256	100

См. Также

Калькулятор дробей

Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби.Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.

Калькулятор смешанных чисел

Калькулятор упрощенных дробей

Калькулятор десятичных дробей

Калькулятор дробей в десятичную

Калькулятор дробей большого числа

Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.

В математике дробь — это число, которое представляет собой часть целого.Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби

числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 ломтиками. 1 из этих 8 ломтиков будет составлять числитель дроби, а всего 8 ломтиков, составляющих весь пирог, будут знаменателем. Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа.Обратите внимание, что знаменатель дроби не может быть равен 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.

Дополнение:

В отличие от сложения и вычитания целых чисел, таких как 2 и 8, дроби требуют общего знаменателя для выполнения этих операций. Один из способов найти общий знаменатель заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.

Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.

Альтернативный метод поиска общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме.В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.

Кратное 2: 2, 4, 6, 8 10, 12

Кратное 4: 4, 8, 12

Кратное 6: 6, 12

Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.

Вычитание:

Вычитание фракции по существу то же, что и сложение фракции. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к уравнениям ниже для пояснения.

Умножение:

Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель.По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.

Дивизион:

Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число, обратное числу , равно —

. Когда a является дробью, это, по сути, включает замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.

Упрощение:

Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.

, например, более громоздкий, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной, так и в смешанной форме чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.

Преобразование между дробями и десятичными дробями:

Преобразовать десятичные дроби в дроби очень просто. Однако необходимо понимать, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 ¹, второй — 10 ², третий — 10 ³ и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 ⁴ или 10 000. В результате дробь составит

, что упрощается до, поскольку наибольший общий делитель между числителем и знаменателем равен 2.

Точно так же дроби со знаменателями, которые являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь

. Чтобы преобразовать эту дробь в десятичную дробь, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 ^-1, можно преобразовать в 0,5. Если бы была дробь, десятичная дробь была бы 0,05, и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.

Преобразование общей инженерной дроби в десятичную дробь

В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.

Ноябрь 2024
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30