Точная и приблизительная таблицы факториалов (1-255)
Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Точная и приблизительная таблицы факториалов (1-255)
Точная и приблизительная таблицы факториалов (1-255)
Факториал n! произвольного целого числа n≥0 определяется по формуле:
Приблизительная таблица факториалов. (1-255)
Факториал
Значение
Факториал
Значение
Факториал
Значение
1!
1
86!
2,42*10130
171!
1,24*10309
2!
2
87!
2,11*10132
172!
2,13*10311
3!
6
88!
1,85*10134
173!
3,69*10313
4!
24
89!
1,65*10136
174!
6,43*10315
5!
1,2*102
90!
1,49*10138
175!
1,12*10318
6!
7,2*102
91!
1,35*10140
176!
1,98*10320
7!
5,04*103
92!
1,24*10142
177!
3,50*10322
8!
4,03*104
93!
1,16*10144
178!
6,24*10324
9!
3,62*105
94!
1,09*10146
179!
1,12*10327
10!
3,62*106
95!
1,03*10148
180!
2,01*10329
11!
3,99*107
96!
9,92*10149
181!
3,64*10331
12!
4,79
97!
9,62*10151
182!
6,62*10333
13!
6,22*109
98!
9,43*10153
183!
1,21*10336
14!
8,71*1010
99!
9,33*10155
184!
2,23*10338
15!
1,30*1012
100!
9,33*10157
185!
4,12*10340
16!
2,09*1013
101!
9,43*10159
186!
7,68*10342
17!
3,55*1014
102!
9,61*10161
187!
1,43*10345
18!
6,40*1015
103!
9,9*10163
188!
2,69*10347
19!
1,21*1017
104!
1,03*10166
189!
5,09*10349
20!
2,43*1018
105!
1,08*10168
190!
9,68*10351
21!
5,10*1019
106!
1,15*10170
191!
1,85*10354
22!
1,12*1021
107!
1,23*10172
192!
3,55*10356
23!
2,58*1022
108!
1,32*10174
193!
6,85*10358
24!
6,20*1023
109!
1,44*10176
194!
1,33*10361
25!
1,55*1025
110!
1,59*10178
195!
2,59*10363
26!
4,03*1026
111!
1,76*10180
196!
5,08*10365
27!
1,08*1028
112!
1,97*10182
197!
1,00*10368
28!
3,05*1029
113!
2,23*10184
198!
1,98*10370
29!
8,84*1030
114!
2,54*10186
199!
3,94*10372
30!
2,65*1032
115!
2,93*10188
200!
7,89*10374
31!
8,22*1033
116!
3,39*10190
201!
1,59*10377
32!
2,63*1035
117!
3,97*10192
202!
3,20*10379
33!
8,68*1036
118!
4,68*10194
203!
6,50*10381
34!
2,95*1038
119!
5,57*10196
204!
1,33*10384
35!
1,03*1040
120!
6,69*10198
205!
2,72*10386
36!
3,72*1041
121!
8,09*10200
206!
5,60*10388
37!
1,38*1043
122!
9,88*10202
207!
1,16*10391
38!
5,23*1044
123!
1,21*10205
208!
2,41*10393
39!
2,04*1046
124!
1,51*10207
209!
5,04*10395
40!
8,16*1047
125!
1,88*10209
210!
1,06*10398
41!
3,35*1049
126!
2,37*10211
211!
2,23*10400
42!
1,41*1051
127!
3,01*10213
212!
4,73*10402
43!
6,04*1052
128!
3,86*10215
213!
1,01*10405
44!
2,66*1054
129!
4,97*10217
214!
2,16*10407
45!
1,19*1056
130!
6,47*10219
215!
4,64*10409
46!
5,50*1057
131!
8,47*10221
216!
1,00*10412
47!
2,59*1059
132!
1,12*10224
217!
2,17*10414
48!
1,24*1061
133!
1,49*10226
218!
4,74*10416
49!
6,08*1062
134!
1,99*10228
219!
1,04*10419
50!
3,04*1064
135!
2,69*10230
220!
2,28*10421
51!
1,55*1066
136!
3,66*10232
221!
5,04*10423
52!
8,07*1067
137!
5,01*10234
222!
1,12*10426
53!
4,28*1069
138!
6,92*10236
223!
2,50*10428
54!
2,31*1071
139!
9,62*10238
224!
5,60*10430
55!
1,27*1073
140!
1,35*10241
225!
1,30*10433
56!
7,11*1074
141!
1,90*10243
226!
2,85*10435
57!
4,05*1076
142!
2,7*10245
227!
6,46*10437
58!
2,35*1078
143!
3,85*10247
228!
1,47*10440
59!
1,39*1080
144!
5,55*10249
229!
3,37*10442
60!
8,32*1081
145!
8,05*10251
230!
7,76*10444
61!
5,08*1083
146!
1,17*10254
231!
1,79*10447
62!
3,15*1085
147!
1,73*10256
232!
4,16*10449
63!
1,98*1087
148!
2,56*10258
233!
9,69*10451
64!
1,27*1089
149!
3,81*10260
234!
2,67*10454
65!
8,25*1090
150!
5,71*10262
235!
5,33*10456
66!
5,44*1092
151!
8,63*10264
236!
1,26*10459
67!
3,65*1094
152!
1,31*10267
237!
2,98*10461
68!
2,48*1096
153!
2,01*10269
238!
7,09*10463
69!
1,71*1098
154!
3,09*10271
239!
1,70*10466
70!
1,20*10100
155!
4,79*10273
240!
4,07*10468
71!
8,50*10101
156!
7,47*10275
241!
9,80*10470
72!
6,12*10103
157!
1,17*10278
242!
2,37*10473
73!
4,47*10105
158!
1,85*10280
243!
5,77*10475
74!
3,31*10107
159!
2,95*10282
244!
1,41*10478
75!
2,48*10109
160!
4,71*10284
245!
3,45*10480
76!
1,89*10111
161!
7,59*10286
246!
8,48*10482
77!
1,45*10113
162!
1,23*10289
247!
2,09*10485
78!
1,13*10115
163!
2,00*10291
248!
5,19*10487
79!
8,95*10116
164!
3,29*10293
249!
1,29*10490
80!
7,16*10118
165!
5,42*10295
250!
3,23*10492
81!
5,80*10120
166!
9,00*10297
251!
8,11*10494
82!
4,75*10122
167!
1,50*10300
252!
2,04*10497
83!
3,95*10124
168!
2,53*10302
253!
5,17*10499
84!
3,31*10126
169!
4,27*10304
254!
1,31*10502
85!
2,82*10128
170!
7,26*10306
255!
3,35*10504
Точная таблица факториалов (1-255)
1!=1
2!=2
3!=6
4!= 24
5!=120
6!=720
7!=5040
8!=40320
9!=362880
10!=3628800
11!=39916800
12!=479001600
13!=6227020800
14!=87178291200
15!=1307674368000
16!=20922789888000
17!=355687428096000
18!=6402373705728000
19!=121645100408832000
20!=2432902008176640000
21!= 51090942171709440000
22!=1124000727777607680000
23!=25852016738884976640000
24!=620448401733239439360000
25!=15511210043330985984000000
26!=403291461126605635584000000
27!=10888869450418352160768000000
28!=304888344611713860501504000000
29!=8841761993739701954543616000000
30!=265252859812191058636308480000000
31!=8222838654177922817725562880000000
32!=263130836933693530167218012160000000
33!=8683317618811886495518194401280000000
34!=295232799039604140847618609643520000000
35!=10333147966386144929666651337523200000000
36!=371993326789901217467999448150835200000000
37!=13763753091226345046315979581580902400000000
38!=523022617466601111760007224100074291200000000
39!=20397882081197443358640281739902897356800000000
40!=815915283247897734345611269596115894272000000000
41!=33452526613163807108170062053440751665152000000000
42!=1405006117752879898543142606244511569936384000000000
43!=60415263063373835637355132068513997507264512000000000
44!=2658271574788448768043625811014615890319638528000000000
45!=119622220865480194561963161495657715064383733760000000000
46!=5502622159812088949850305428800254892961651752960000000000
47!=258623241511168180642964355153611979969197632389120000000000
48!=12413915592536072670862289047373375038521486354677760000000000
49!=608281864034267560872252163321295376887552831379210240000000000
50!=30414093201713378043612608166064768844377641568960512000000000000
51!=1551118753287382280224243016469303211063259720016986112000000000000
52!=80658175170943878571660636856403766975289505440883277824000000000000
53!=4274883284060025564298013753389399649690343788366813724672000000000000
54!=230843697339241380472092742683027581083278564571807941132288000000000000
55!=12696403353658275925965100847566516959580321051449436762275840000000000000
56!=710998587804863451854045647463724949736497978881168458687447040000000000000
57!=40526919504877216755680601905432322134980384796226602145184481280000000000000
58!=2350561331282878571829474910515074683828862318181142924420699914240000000000000
59!=138683118545689835737939019720389406345902876772687432540821294940160000000000000
60!=8320987112741390144276341183223364380754172606361245952449277696409600000000000000
61!=507580213877224798800856812176625227226004528988036003099405939480985600000000000000
62!=31469973260387937525653122354950764088012280797258232192163168247821107200000000000000
63!=1982608315404440064116146708361898137544773690227268628106279599612729753600000000000000
64!=126886932185884164103433389335161480802865516174545192198801894375214704230400000000000000
65!=8247650592082470666723170306785496252186258551345437492922123134388955774976000000000000000
66!=544344939077443064003729240247842752644293064388798874532860126869671081148416000000000000000
67!=36471110918188685288249859096605464427167635314049524593701628500267962436943872000000000000000
68!=2480035542436830599600990418569171581047399201355367672371710738018221445712183296000000000000000
69!=171122452428141311372468338881272839092270544893520369393648040923257279754140647424000000000000000
70!=11978571669969891796072783721689098736458938142546425857555362864628009582789845319680000000000000000
71!=850478588567862317521167644239926010288584608120796235886430763388588680378079017697280000000000000000
72!=61234458376886086861524070385274672740778091784697328983823014963978384987221689274204160000000000000000
73!=4470115461512684340891257138125051110076800700282905015819080092370422104067183317016903680000000000000000
74!=330788544151938641225953028221253782145683251820934971170611926835411235700971565459250872320000000000000000
75!=24809140811395398091946477116594033660926243886570122837795894512655842677572867409443815424000000000000000000
76!=1885494701666050254987932260861146558230394535379329335672487982961844043495537923117729972224000000000000000000
77!=145183092028285869634070784086308284983740379224208358846781574688061991349156420080065207861248000000000000000000
78!=11324281178206297831457521158732046228731749579488251990048962825668835325234200766245086213177344000000000000000000
79!=894618213078297528685144171539831652069808216779571907213868063227837990693501860533361810841010176000000000000000000
80!=71569457046263802294811533723186532165584657342365752577109445058227039255480148842668944867280814080000000000000000000
81!=5797126020747367985879734231578109105412357244731625958745865049716390179693892056256184534249745940480000000000000000000
82!=475364333701284174842138206989404946643813294067993328617160934076743994734899148613007131808479167119360000000000000000000
83!=39455239697206586511897471180120610571436503407643446275224357528369751562996629334879591940103770870906880000000000000000000
84!=3314240134565353266999387579130131288000666286242049487118846032383059131291716864129885722968716753156177920000000000000000000
85!=281710411438055027694947944226061159480056634330574206405101912752560026159795933451040286452340924018275123200000000000000000000
86!=24227095383672732381765523203441259715284870552429381750838764496720162249742450276789464634901319465571660595200000000000000000000
87!=2107757298379527717213600518699389595229783738061356212322972511214654115727593174080683423236414793504734471782400000000000000000000
88!=185482642257398439114796845645546284380220968949399346684421580986889562184028199319100141244804501828416633516851200000000000000000000
89!=16507955160908461081216919262453619309839666236496541854913520707833171034378509739399912570787600662729080382999756800000000000000000000
90!=1485715964481761497309522733620825737885569961284688766942216863704985393094065876545992131370884059645617234469978112000000000000000000000
91!=135200152767840296255166568759495142147586866476906677791741734597153670771559994765685283954750449427751168336768008192000000000000000000000
92!=12438414054641307255475324325873553077577991715875414356840239582938137710983519518443046123837041347353107486982656753664000000000000000000000
93!=1156772507081641574759205162306240436214753229576413535186142281213246807121467315215203289516844845303838996289387078090752000000000000000000000
94!=108736615665674308027365285256786601004186803580182872307497374434045199869417927630229109214583415458560865651202385340530688000000000000000000000
95!=10329978488239059262599702099394727095397746340117372869212250571234293987594703124871765375385424468563282236864226607350415360000000000000000000000
96!=991677934870949689209571401541893801158183648651267795444376054838492222809091499987689476037000748982075094738965754305639874560000000000000000000000
97!=96192759682482119853328425949563698712343813919172976158104477319333745612481875498805879175589072651261284189679678167647067832320000000000000000000000
98!=9426890448883247745626185743057242473809693764078951663494238777294707070023223798882976159207729119823605850588608460429412647567360000000000000000000000
99!=933262154439441526816992388562667004907159682643816214685929638952175999932299156089414639761565182862536979208272237582511852109168640000000000000000000000
100!=93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
101!=9425947759838359420851623124482936749562312794702543768327889353416977599316221476503087861591808346911623490003549599583369706302603264000000000000000000000000
102!=961446671503512660926865558697259548455355905059659464369444714048531715130254590603314961882364451384985595980362059157503710042865532928000000000000000000000000
103!=99029007164861804075467152545817733490901658221144924830052805546998766658416222832141441073883538492653516385977292093222882134415149891584000000000000000000000000
104!=10299016745145627623848583864765044283053772454999072182325491776887871732475287174542709871683888003235965704141638377695179741979175588724736000000000000000000000000
105!=1081396758240290900504101305800329649720646107774902579144176636573226531909905153326984536526808240339776398934872029657993872907813436816097280000000000000000000000000
106!=114628056373470835453434738414834942870388487424139673389282723476762012382449946252660360871841673476016298287096435143747350528228224302506311680000000000000000000000000
107!=12265202031961379393517517010387338887131568154382945052653251412013535324922144249034658613287059061933743916719318560380966506520420000368175349760000000000000000000000000
108!=1324641819451828974499891837121832599810209360673358065686551152497461815091591578895743130235002378688844343005686404521144382704205360039762937774080000000000000000000000000
109!=144385958320249358220488210246279753379312820313396029159834075622223337844983482099636001195615259277084033387619818092804737714758384244334160217374720000000000000000000000000
110!=15882455415227429404253703127090772871724410234473563207581748318444567162948183030959960131517678520479243672638179990208521148623422266876757623911219200000000000000000000000000
111!=1762952551090244663872161047107075788761409536026565516041574063347346955087248316436555574598462315773196047662837978913145847497199871623320096254145331200000000000000000000000000
112!=197450685722107402353682037275992488341277868034975337796656295094902858969771811440894224355027779366597957338237853638272334919686385621811850780464277094400000000000000000000000000
113!=22311927486598136465966070212187151182564399087952213171022161345724023063584214692821047352118139068425569179220877461124773845924561575264739138192463311667200000000000000000000000000
114!=2543559733472187557120132004189335234812341496026552301496526393412538629248600474981599398141467853800514886431180030568224218435400019580180261753940817530060800000000000000000000000000
115!=292509369349301569068815180481773552003419272043053514672100535242441942363589054622883930786268803187059211939585703515345785120071002251720730101703194015956992000000000000000000000000000
116!=33931086844518982011982560935885732032396635556994207701963662088123265314176330336254535971207181169698868584991941607780111073928236261199604691797570505851011072000000000000000000000000000
117!=3969937160808720895401959629498630647790406360168322301129748464310422041758630649341780708631240196854767624444057168110272995649603642560353748940315749184568295424000000000000000000000000000
118!=468452584975429065657431236280838416439267950499862031533310318788629800927518416622330123618486343228862579684398745837012213486653229822121742374957258403779058860032000000000000000000000000000
119!=55745857612076058813234317117419771556272886109483581752463927935846946310374691578057284710599874844234646982443450754604453404911734348832487342619913750049708004343808000000000000000000000000000
120!=6689502913449127057588118054090372586752746333138029810295671352301633557244962989366874165271984981308157637893214090552534408589408121859898481114389650005964960521256960000000000000000000000000000
121!=809429852527344373968162284544935082997082306309701607045776233628497660426640521713391773997910182738287074185078904956856663439318382745047716214841147650721760223072092160000000000000000000000000000
122!=98750442008336013624115798714482080125644041369783596059584700502676714572050143649033796427745042294071023050579626404736512939596842694895821378210620013388054747214795243520000000000000000000000000000
123!=12146304367025329675766243241881295855454217088483382315328918161829235892362167668831156960612640202170735835221294047782591091570411651472186029519906261646730733907419814952960000000000000000000000000000
124!=1506141741511140879795014161993280686076322918971939407100785852066825250652908790935063463115967385069171243567440461925041295354731044782551067660468376444194611004520057054167040000000000000000000000000000
125!=188267717688892609974376770249160085759540364871492425887598231508353156331613598866882932889495923133646405445930057740630161919341380597818883457558547055524326375565007131770880000000000000000000000000000000
126!=23721732428800468856771473051394170805702085973808045661837377170052497697783313457227249544076486314839447086187187275319400401837013955325179315652376928996065123321190898603130880000000000000000000000000000000
127!=3012660018457659544809977077527059692324164918673621799053346900596667207618480809067860692097713761984609779945772783965563851033300772326297773087851869982500270661791244122597621760000000000000000000000000000000
128!=385620482362580421735677065923463640617493109590223590278828403276373402575165543560686168588507361534030051833058916347592172932262498857766114955245039357760034644709279247692495585280000000000000000000000000000000
129!=49745042224772874403902341504126809639656611137138843145968864022652168932196355119328515747917449637889876686464600208839390308261862352651828829226610077151044469167497022952331930501120000000000000000000000000000000
130!=6466855489220473672507304395536485253155359447828049608975952322944781961185526165512707047229268452925683969240398027149120740074042105844737747799459310029635780991774612983803150965145600000000000000000000000000000000
131!=847158069087882051098456875815279568163352087665474498775849754305766436915303927682164623187034167333264599970492141556534816949699515865660644961729169613882287309922474300878212776434073600000000000000000000000000000000
132!=111824865119600430744996307607616902997562475571842633838412167568361169672820118454045730260688510087990927196104962685462595837360336094267205134948250389032461924909766607715924086489297715200000000000000000000000000000000
133!=14872707060906857289084508911813048098675809251055070300508818286592035566485075754388082124671571841702793317081960037166525246368924700537538282948117301741317436012998958826217903503076596121600000000000000000000000000000000
134!=1992942746161518876737324194182948445222558439641379420268181650403332765909000151088003004705990626788174304488982644980314383013435909872030129915047718433336536425741860482713199069412263880294400000000000000000000000000000000
135!=269047270731805048359538766214698040105045389351586221736204522804449923397715020396880405635308734616403531106012657072342441706813847832724067538531441988500432417475151165166281874370655623839744000000000000000000000000000000000
136!=36590428819525486576897272205198933454286172951815726156123815101405189582089242773975735166401987907830880230417721361838572072126683305250473185240276110436058808776620558462614334914409164842205184000000000000000000000000000000000
137!=5012888748274991661034926292112253883237205694398754483388962668892510972746226260034675717797072343372830591567227826571884373881355612819314826377917827129740056802397016509378163883274055583382110208000000000000000000000000000000000
138!=691778647261948849222819828311491035886734385827028118707676848307166514238979223884785249055995983385450621636277440066920043595627074569065446040152660143904127838730788278294186615891819670506731208704000000000000000000000000000000000
139!=96157231969410890041971956135297253988256079629956908500367081914696145479218112119985149618783441690577636407442564169301886059792163365100096999581219760002673769583579570682891939608962934200435638009856000000000000000000000000000000000
140!=13462012475717524605876073858941615558355851148193967190051391468057460367090535696797920946629681836680869097041958983702264048370902871114013579941370766400374327741701139895604871545254810788060989321379840000000000000000000000000000000000
141!=1898143759076170969428526414110767793728175011895349373797246196996101911759765533248506853474785138972002542682916216702019230820297304827075914771733278062452780211579860725280286887880928321116599494314557440000000000000000000000000000000000
142!=269536413788816277658850750803729026709400851689139611079208959973446471469886705721287973193419489734024361060974102771686730776482217285444779897586125484868294790044340222989800738079091821598557128192667156480000000000000000000000000000000000
143!=38543707171800727705215657364933250819444321791546964384326881276202845420193798918144180166658987031965483631719296696351202501036957071818603525354815944336166154976340651887541505545310130488593669331551403376640000000000000000000000000000000000
144!=5550293832739304789551054660550388117999982337982762871343070903773209740507907044212761943998894132603029642967578724274573160149321818341878907651093495984407926316593053871805976798524658790357488383743402086236160000000000000000000000000000000000
145!=804792605747199194484902925779806277109997439007500616344745281047115412373646521410850481879839649227439298230298915019813108221651663659572441609408556917739149315905992811411866635786075524601835815642793302504243200000000000000000000000000000000000
146!=117499720439091082394795827163851716458059626095095089986332811032878850206552392125984170354456588787206137541623641592892713800361142894297576474973649309989915800122274950466132528824767026591868029083847822165619507200000000000000000000000000000000000
147!=17272458904546389112034986593086202319334765035978978227990923221833190980363201642519673042105118551719302218618675314155228928653088005461743741821126448568517622617974417718521481737240752909004600275325629858346067558400000000000000000000000000000000000
148!=2556323917872865588581178015776757943261545225324888777742656636831312265093753843092911610231557545654456728355563946494973881440657024808338073789526714388140608147460213822341179297111631430532680840748193219035217998643200000000000000000000000000000000000
149!=380892263763056972698595524350736933545970238573408427883655838887865527498969322620843829924502074302514052524979028027751108334657896696442372994639480443832950613971571859528835715269633083149369445271480789636247481797836800000000000000000000000000000000000
150!=57133839564458545904789328652610540031895535786011264182548375833179829124845398393126574488675311145377107878746854204162666250198684504466355949195922066574942592095735778929325357290444962472405416790722118445437122269675520000000000000000000000000000000000000
151!=8627209774233240431623188626544191544816225903687700891564804750810154197851655157362112747789971982951943289690774984828562603780001360174419748328584232052816331406456102618328128950857189333333217935399039885261005462721003520000000000000000000000000000000000000
152!=1311335885683452545606724671234717114812066337360530535517850322123143438073451583919041137664075741408695380032997797693941515774560206746511801745944803272028082373781327597985875600530292778666649126180654062559672830333592535040000000000000000000000000000000000000
153!=200634390509568239477828874698911718566246149616161171934231099284840946025238092339613294062603588435530393145048663047173051913507711632216305667129554900620296603188543122491838966881134795135997316305640071571629943041039657861120000000000000000000000000000000000000
154!=30897696138473508879585646703632404659201907040888820477871589289865505687886666220300447285640952619071680544337494109264649994680187591361311072737951454695525676891035640863743200899694758450943586711068571022031011228320107310612480000000000000000000000000000000000000
155!=4789142901463393876335775239063022722176295591337767174070096339929153381622433264146569329274347655956110484372311586936020749175429076661003216274382475477806479918110524333880196139452687559896255940215628508414806740389616633144934400000000000000000000000000000000000000
156!=747106292628289444708380937293831544659502112248691679154935029028947927533099589206864815366798234329153235562080607562019236871366935959116501738803666174537810867225241796085310597754619259343815926673638047312709851500780194770609766400000000000000000000000000000000000000
157!=117295687942641442819215807155131552511541831623044593627324799557544824622696635505477776012587322789677057983246655387237020188804608945581290772992175589402436306154362961985393763847475223716979100487761173428095446685622490578985733324800000000000000000000000000000000000000
158!=18532718694937347965436097530510785296823609396441045793117318330092082290386068409865488609988797000768975161352971551183449189831128213401843942132763743125584936372389347993692214687901085347282697877066265401639080576328353511479745865318400000000000000000000000000000000000000
159!=2946702272495038326504339507351214862194953894034126281105653614484641084171384877168612688988218723122267050655122476638168421183149385930893186799109435156968004883209906330997062135376272570217948962453536198860613811636208208325279592585625600000000000000000000000000000000000000
160!=471472363599206132240694321176194377951192623045460204976904578317542573467421580346978030238114995699562728104819596262106947389303901748942909887857509625114880781313585012959529941660203611234871833992565791817698209861793313332044734813700096000000000000000000000000000000000000000
161!=75907050539472187290751785709367294850142012310319093001281637109124354328254874435863462868336514307629599224875954998199218529677928181579808491945059049643495805791487187086484320607292781408814365272803092482649411787748723446459202305005715456000000000000000000000000000000000000000
162!=12296942187394494341101789284917501765723005994271693066207625211678145401177289658609880984670515317835995074429904709708273401807824365415928975695099566042246320538220924308010459938381430588227927174194100982189204709615293198326390773410925903872000000000000000000000000000000000000000
163!=2004401576545302577599591653441552787812849977066285969791842909503537700391898214353410600501293996807267197132074467682448564494675371562796423038301229264886150247730010662205704969956173185881152129393638460096840367667292791327201696065980922331136000000000000000000000000000000000000000
164!=328721858553429622726333031164414657201307396238870899045862237158580182864271307153959338482212215476391820329660212699921564577126760936298613378281401599441328640627721748601735615072812402484508949220556707455881820297436017777661078154820871262306304000000000000000000000000000000000000000
165!=54239106661315887749844950142128418438215720379413698342567269131165730172604765680403290849565015553604650354393935095487058155225915554489271207416431263907819225703574088519286376487014046409943976621391856730220500349076942933314077895545443758280540160000000000000000000000000000000000000000
166!=9003691705778437366474261723593317460743809582982673924866166675773511208652391102946946281027792581898371958829393225850851653767501982045219020431127589808697991466793298694201538496844331704050700119151048217216603057946772526930136930660543663874569666560000000000000000000000000000000000000000
167!=1503616514864999040201201707840084015944216200358106545452649834854176371844949314192140028931641361177028117124508668717092226179172831001551576411998307498052564574954480881931656928973003394576466919898225052275172710677111011997332867420310791867053134315520000000000000000000000000000000000000000
168!=252607574497319838753801886917134114678628321660161899636045172255501630469951484784279524860515748677740723676917456344471493998101035608260664837215715659672830848592352788164518364067464570288846442542901808782229015393754650015551921726612213033664926565007360000000000000000000000000000000000000000
169!=42690680090047052749392518888995665380688186360567361038491634111179775549421800928543239701427161526538182301399050122215682485679075017796052357489455946484708413412107621199803603527401512378815048789750405684196703601544535852628274771797464002689372589486243840000000000000000000000000000000000000000
170!=7257415615307998967396728211129263114716991681296451376543577798900561843401706157852350749242617459511490991237838520776666022565442753025328900773207510902400430280058295603966612599658257104398558294257568966313439612262571094946806711205568880457193340212661452800000000000000000000000000000000000000000
171!=1241018070217667823424840524103103992616605577501693185388951803611996075221691752992751978120487585576464959501670387052809889858690710767331242032218484364310473577889968548278290754541561964852153468318044293239598173696899657235903947616152278558180061176365108428800000000000000000000000000000000000000000
172!=213455108077438865629072570145733886730056159330291227886899710221263324938130981514753340236723864719151973034287306573083301055694802251980973629541579310661401455397074590303866009781148657954570396550703618437210885875866741044575478989978191912006970522334798649753600000000000000000000000000000000000000000
173!=36927733697396923753829554635211962404299715564140382424433649868278555214296659802052327860953228596413291334931704037143411082635200789592708437910693220744422451783693904122568819692138717826140678603271725989637483256524946200711557865266227200777205900363920166407372800000000000000000000000000000000000000000
174!=6425425663347064733166342506526881458348150508160426541851455077080468607287618805557105047805861775775912692278116502462953528378524937389131268196460620409529506610362739317326974626432136901748478076969280322196922086635340638923811068556323532935233826663322108954882867200000000000000000000000000000000000000000
175!=1124449491085736328304109938642204255210926338928074644824004638489082006275333290972493383366025810760784721148670387931016867466241864043097971934380608571667663656813479380532220559625623957805983663469624056384461365161184611811666936997356618263665919666081369067104501760000000000000000000000000000000000000000000
176!=197903110431089593781523349201027948917123035651341137489024816374078433104458659211158835472420542693898110922165988275858968674058568071585243060450987108613508803599172370973670818494109816573853124770653833923665200268368491678853380911534764814405201861230320955810392309760000000000000000000000000000000000000000000
177!=35028850546302858099329632808581946958330777310287381335557392498211882659489182680375113878618436056819965633223379924827037455308366548670588021699824718224591058237053509662339734873457437533572003084405728604488740447501223027157048421341653372149720729437766809178439438827520000000000000000000000000000000000000000000
178!=6235135397241908741680674639927586558582878361231153877729215864681715113389074517106770270394081618113953882713761626619212667044889245663364667862568799843977208366195524719896472807475423880975816549024219691598995799655217698833954618998814300242650289839922492033762220111298560000000000000000000000000000000000000000000
179!=1116089236106301664760840760547037993986335226660376544113529639778027005296644338562111878400540609642397745005763331164839067401035174973742275547399815172071920297548998924861468632538100874694671162275335324796220248138283968091277876800787759743434401881346126074043437399922442240000000000000000000000000000000000000000000
180!=200896062499134299656951336898466838917540340798867777940435335160044860953395980941180138112097309735631594101037399609671032132186331495273609598531966730972945653558819806475064353856858157445040809209560358463319644664891114256430017824141796753818192338642302693327818731986039603200000000000000000000000000000000000000000000
181!=36362187312343308237908191978622497844074801684595067807218795663968119832564672550353604998289613062149318532287769329350456815925726000644523337334285978306103163294146384971986648048091326497552386466930424881860855684345291680413833226169665212441092813294256787492335190489473168179200000000000000000000000000000000000000000000
182!=6617918090846482099299290940109294607621613906596302340913820810842197809526770404164356109688709577311175972876374017941783140498482132117303247394840048051710775719534642064901569944752621422554534336981337328498675734550843085835317647162879068664278892019554735323605004669084116608614400000000000000000000000000000000000000000000
183!=1211079010624906224171770242040000913194755344907123328387229208384122199143398983962077168073033852647945203036376445283346314711222230177466494273255728793463071956674839497876987299889729720327479783667584731115257659422804284707863129430806869565563037239578516564219715854442393339376435200000000000000000000000000000000000000000000
184!=222838537954982745247605724535360168027834983462910692423250174342678484642385413049022198925438228887221917358693265932135721906864890352653834946279054097997205240028170467609365663179710268540256280194835590525207409333795988386246815815268464000063598852082447047816427717217400374445264076800000000000000000000000000000000000000000000
185!=41225129521671807870807059039041631085149471940638478098301282253395519658841301414069106801206072344136054711358254197445108552770004715240959465061625008129482969405211536507732647688246399679947411836044584247163370726752257851455660925824665840011765787635252703846039127685219069272373854208000000000000000000000000000000000000000000000
186!=7667874091030956263970112981261743381837801780958756926284038499131566656544482063016853865024329456009306176312635280724790190815220877034818460501462251512083832309369345790438272470013830340470218601504292669972386955175919960370752932203387846242188436500157002915363277749450746884661536882688000000000000000000000000000000000000000000000
187!=1433892455022788821362411127495946012403668933039287545215115199337602964773818145784151672759549608273740254970462797495535765682446304005511052113773441032759676641852067662811956951892586273667930878481302729284836360617897032589330798322033527247289237625529359545172932939147289667431707397062656000000000000000000000000000000000000000000000
188!=269571781544284298416133291969237850331889759411386058500441657475469357377477811407420514478795326355463167934447005929160723948299905153036077797389406914158819208668188720608647906955806219449571005154484913105549235796164642126794190084542303122490376673599519594492511392559690457477160990647779328000000000000000000000000000000000000000000000
189!=50949066711869732400649192182185953712727164528751965056583473262863708544343306356002477236492316681182538739610484120611376826228682073923818703706597906776016830438287668195034454414647375475968919974197648576948805565475117361964101925978495290150681191310309203359084653193781496463183427232430292992000000000000000000000000000000000000000000000
190!=9680322675255249156123346514615331205418161260462873360750859919944104623425228207640470674933540169424682360525991982916161596983449594045525553704253602287443197783274656957056546338783001340434094795097553229620273057440272298773179365935914105128629426348958748638226084106818484328004851174161755668480000000000000000000000000000000000000000000000
191!=1848941630973752588819559184291528260234868800748408811903414244709323983074218587659329898912306172360114330860464468736986865023838872462695380757512438036901650776605459478797800350707553256022912105863632666857472153971092009065677258893759594079568220432651120989901182064402330506648926574264895332679680000000000000000000000000000000000000000000000
192!=354996793146960497053355363383973425965094809743694491885455534984190204750249968830591340591162785093141951525209177997501478084577063512837513105442388103085116949108248219929177667335850225156399124325817472036634653562449665740610033707601842063277098323069015230061026956365247457276593902258859903874498560000000000000000000000000000000000000000000000
193!=68514381077363375931297585133106871211263298280533036933892918251948709516798243984304128734094417522976396644365371353517785270323373257977640029350380903895427571177891906446331289795819093455185030994882772103070488137552785487937736505567155518212479976352319939401778202578492759254382623135959961447778222080000000000000000000000000000000000000000000000
194!=13291789929008494930671731515822733014985079866423409165175226140878049646258859332955000974414316999457420949006882042582450342442734412047662165693973895355712948808511029850588270220388904130305896013007257787995674698685240384659920882080028170533221115412350068243944971300227595295350228888376232520868975083520000000000000000000000000000000000000000000000
195!=2591899036156656511480987645585432937922090573952564787209169097471219681020477569926225190010791814894197085056341998303577816776333210349294122310324909594364025017659650820864712692975836305409649722536415268659156566243621875008684572005605493253978117505408263307569269403544381082593294633233365341569450141286400000000000000000000000000000000000000000000000
196!=508012211086704676250273578534744855832729752494702698292997143104359057480013603705540137242115195719262628671043031667501252088161309228461647972823682280495348903461291560889483687823263915860291345617137392657194686983749887501702176113098676677779711031060019608283576803094698692188285748113739606947612227692134400000000000000000000000000000000000000000000000
197!=100078405584080821221303894971344736599047761241456431563720437191558734323562679929991407036696693556694737848195477238497746661367777918006944650646265409257583733981874437495228286501182991424477395086576066353467353335798727837835328694280439305522603073118823862831864630209655642361092292378406702568679608855350476800000000000000000000000000000000000000000000000
198!=19815524305648002601818171204326257846611456725808373449616646563928629396065410626138298593265945324225558093942704493222553838950820027765375040827960551033001579328411138624055200727234232302046524227142061137986535960488148111891395081467526982493475408477527124840709196781511817187496273890924527108598562553359394406400000000000000000000000000000000000000000000000
199!=3943289336823952517761816069660925311475679888435866316473712666221797249817016714601521420059923119520886060694598194151288213951213185525309633124764149655567314286353816586186984944719612228107258321201270166459320656137141474266387621212037869516201606287027897843301130159520851620311758504293980894611113948118519486873600000000000000000000000000000000000000000000000
200!=788657867364790503552363213932185062295135977687173263294742533244359449963403342920304284011984623904177212138919638830257642790242637105061926624952829931113462857270763317237396988943922445621451664240254033291864131227428294853277524242407573903240321257405579568660226031904170324062351700858796178922222789623703897374720000000000000000000000000000000000000000000000000
201!=158520231340322891214025006000369197521322331515121825922243249182116249442644071926981161086408909404739619639922847404881786200838770058117447251615518816153806034311423426764716794777728411569911784512291060691664690376713087265508782372723922354551304572738521493300705432412738235136532691872618031963366780714364483372318720000000000000000000000000000000000000000000000000
202!=32021086730745224025233051212074577899307110966054608836293136334787482387414102529250194539454599699757403167264415175786120812569431551739724344826334800863068818930907532206472792545101139137122180471482794259716267456096043627632774039290232315619363523693181341646742497347373123497579603758268842456600089704301625641208381440000000000000000000000000000000000000000000000000
203!=6500280606341280477122309396051139313559343526109085593767506675961858924645062813437789491509283739050752842954676280684582524951594605003164041999745964575202970242974229037913976886655531244835802635711007234722402293587496856409453129975917160070730795309715812354288726961516744070008659562928575018689818209973230005165301432320000000000000000000000000000000000000000000000000
204!=1326057243693621217332951116794432419966106079326253461128571361896219220627592813941309056267893882766353579962753961259654835090125299420645464567948176773341405929566742723734451284877728373946503737685045475883370067891849358707528438515087100654429082243182025720274900300149415790281766550837429303812722914834538921053721492193280000000000000000000000000000000000000000000000000
205!=271841734957192349553254978942858646093051746261881959531357129188724940228656526857968356534918245967102483892364562058229241193475686381232320236429376238534988215561182258365562513399934316659033266225434322556090863917829118535043329895592855634157961859852315272656354561530630237007762142921673007281608197541080478816012905899622400000000000000000000000000000000000000000000000000
206!=55999397401181624007970525662228881095168659729947683663459568612877337687103244532741481446193158669223111681827099783995223685855991394533857968704451505138207572405603545223305877760386469231760852842439470446554717967072798418218925958492128260636540143129576946167209039675309828823599001441864639500011288693462578636098658615322214400000000000000000000000000000000000000000000000000
207!=11591875262044596169649898812081378386699912564099170518336130702865608901230371618277486659361983844529184118138209655287011302972190218668508599521821461563608967487959933861224316696399999130974496538384970382436826619184069272571317673407870549951763809627822427856612271212789134566484993298465980376502336759546753777672422333371698380800000000000000000000000000000000000000000000000000
208!=2411110054505276003287178952912926704433581813332627467813915186196046651455917296601717225147292639662070296572747608299698351018215565483049788700538864005230665237495666243134657872851199819242695279984073839546859936790286408694834076068837074389966872402587064994175352412260139989828878606080923918312486045985724785755863845341313263206400000000000000000000000000000000000000000000000000
209!=503922001391602684687020401158801681226618598986519140773108273914973750154286714989758900055784161689372691983704250134636955362807053185957405838412622577093209034636594244815143495425900762221723313516671432465293726789169859417220321898386948547503076332140696583782648654162369257874235628670913098927309583611016480222975543676334472010137600000000000000000000000000000000000000000000000000
210!=105823620292236563784274284243348353057589905787169019562352737522144487532400210147849369011714673954768265316577892528273760626189481169051055226066650741189573897273684791411180134039439160066561895838501000817711682625725670477616267598661259194975646029749546282594356217374097544153589482020891750774735012558313460846824864172030239122128896000000000000000000000000000000000000000000000000000
211!=22328783881661914958481873975346502495151470121092663127656427617172486869336444341196216861471796204456103981797935323465763492125980526669772652700063306391000092324747490987759008282321662774044560021923711172537165034028116470777032463317525690139861312277154265627409161865934581816407380706408159413469087649804140238680046340298380454769197056000000000000000000000000000000000000000000000000000
212!=4733702182912325971198157282773458528972111665671644583063162654840567216299326200333597974632020795344694044141162288574741860330707871653991802372413420954892019572846468089404909755852192508097446724647826768577878987213960691804730882223315446309650598202756704313010742315578131345078364709758529795655446581758477730600169824143256656411069775872000000000000000000000000000000000000000000000000000
213!=1008278564960325431865207501230746666671059784788060296192453645481040817071756480671056368596620429408419831402067567466420016250440776662300253905324058663392000169016297703043245777996517004224756152349987101707088224276573627354407677913566190063955577417187178018671288113218141976501691683178566846474610121914555756617836172542513667815557862260736000000000000000000000000000000000000000000000000000
214!=215771612901509642419154405263379786667606793944644903385185080132942734853355886863606062879676771893401843920042459437813883477594326205732254335739348553965888036169487708451254596491254638904097816602897239765316879995186756253843243073503164673686493567278056095995655656228682382971362020200213305145566566089714931916216940924097924912529382523797504000000000000000000000000000000000000000000000000000
215!=46390896773824573120118197131626654133535460698098654227814792228582687993471515675675303519130505957081396442809128779129984947682780134232434682183959939102665927776439857317019738245619747364381030569622906549543129198965152594576297260803180404842596116964782060639065966089166712338842834343045860606296811709288710361986642298681053856193817242616463360000000000000000000000000000000000000000000000000000
216!=10020433703146107793945530580431357292843659510789309313207995121373860606589847385945865560132189286729581631646771816292076748699480508994205891351735346846175840399711009180476263461053865430706302603038547814701315906976472960428480208333486967446000761264392925098038248675260009865190052218097905890960111329206361438189114736515107632937864524405156085760000000000000000000000000000000000000000000000000000
217!=2174434113582705391286180135953604532547074113841280120966134941338127751629996882750252826548685075220319214067349484135380654467787270451742678423326570265620157366737288992163349171048688798463267664859364875790185551813894632412980205208366671935782165194373264746274299962531422140746241331327245578338344158437780432087037897823778356347516601795918870609920000000000000000000000000000000000000000000000000000
218!=474026636761029775300387269637885788095262156817399066370617417211711849855339320439555116187613346398029588666682187541512982673977624958479903896285192317905194305948729000291610119288614158064992350939341542922260450295429029866029684735423934482000512012373371714687797391831850026682680610229339536077759026539436134194974261725583681683758619191510313792962560000000000000000000000000000000000000000000000000000
219!=103811833450665520790784812050696987592862412343010395535165214369364895118319311176262570445087322861168479918003399071591343205601099865907098953286457117621237553002771651063862616124206500616233324855715797899975038614698957540660500957057841651558112130709768405516627628811175155843507053640225358401029226812136513388699363317902826288743137602940758720658800640000000000000000000000000000000000000000000000000000
220!=22838603359146414573972658651153337270429730715462287017736347161260276926030248458777765497919211029457065581960747795750095505232241970499561769723020565876672261660609763234049775547325430135571331468257475537994508495233770658945310210552725163342784668756149049213658078338458534285571551800849578848226429898670032945513859929938621783523490272646966918544936140800000000000000000000000000000000000000000000000000000
221!=5047331342371357620847957561904887536764970488117165430919732722638521200652684909389886175040145637510011493613325262860771106656325475480403151108787545058744569826994757674725000395958920059961264254484902093896786377446663315626913556532152261098755411795108939876218435312799336077111312947987756925458041007606077280958563044516435414158691350254979688998430887116800000000000000000000000000000000000000000000000000000
222!=1120507558006441391828246578742885033161823448362010725664180664425751706544896049884554730858912331527222551582158208355091185677704255556649499546150835003041294501592836203788950087902880253311400664495648264845086575793159256069174809550137801963923701418514184652520492639441452609118711474453282037451685103688549156372800995882648661943229479756605490957651656939929600000000000000000000000000000000000000000000000000000
223!=249873185435436430377698987059663362395086628984728391823112288166942630559511819124255704981537449930570629002821280463185334406128048989132838398791636205678208673855202473444935869602342296488442348182529563060454306401874514103425982529680729837954985416328663177512069858595443931833472658803081894351725778122546461871134622081830651613340173985723024483556319497604300800000000000000000000000000000000000000000000000000000
224!=55971593537537760404604573101364593176499404892579159768377152549395149245330647483833277915864388784447820896631966823753514906972682973565755801329326510071918742943565354051665634790924674413411085992886622125541764634019891159167420086648483483701916733257620551762703648325379440730697875571890344334786574299450407459134155346330065961388198972801957484316615567463363379200000000000000000000000000000000000000000000000000000
225!=12593608545945996091036028947807033464712366100830310947884859323613908580199395683862487531069487476500759701742192535344540854068853669052295055299098464766181717162302204661624767827958051743017494348399489978246897042654475510812669519495908783832931264982964624146608320873210374164407022003675327475326979217376341678305184952924264841312344768880440433971238502679256760320000000000000000000000000000000000000000000000000000000
226!=2846155531383795116574142542204389563024994738787650274221978207136743339125063424552922182021704169689171692593735512987866233019560929205818682497596253037157068078680298253527197529118519693921953722738284735083798731639911465443663311406075385146242465886150005057133480517345544561155986972830624009423897303127053219296971799360883854136589917766979538077499901605512027832320000000000000000000000000000000000000000000000000000000
227!=646077305624121491462330357080396430806673805704796612248389053020040737981389397373513335318926846519441974218777961448245634895440330929720840926954349439434654453860427703550673839109903970520283495061590634864022312082259902655711571689179112428197039756156051147969300077437438615382409042832551650139224687809841080780412598454920634889005911333104355143592477664451230317936640000000000000000000000000000000000000000000000000000000
228!=147305625682299700053411321414330386223921627700693627592632704088569288259756782601161040452715321006432770121881375210200004756160395451976351731345591672191101215480177516409553635317058105278624636874042664748997087154755257805502238345132837633628925064403579661737000417655736004307189261765821776231743228820643766417934072447721904754693347783947792972739084907494880512489553920000000000000000000000000000000000000000000000000000000
229!=33732988281246631312231192603881658445278052743458840718712889236282367011484303215665878263671808510473104357910834923135801089160730558502584546478140492931762178344960651257787782487606306108805041844155770227520332958438954037460012581035419818101023839748419742537773095643163544986346340944373186757069199399927422509706902590528316188824776642524044590757250443816327637360107847680000000000000000000000000000000000000000000000000000000
230!=7758587304686725201813174298892781442413952130995533365303964524344944412641389739603152000644515957408814002319492032321234250506968028455594445689972313374305301019340949789291189972149450405025159624155827152329676580440959428615802893638146558163235483142136540783687811997927615346859658417205832954125915861983307177232587595821512723429698627780530255874167602077755356592824804966400000000000000000000000000000000000000000000000000000000
231!=1792233667382633521618843263044232513197622942259968207385215805123682159320161029848328112148883186161436034535802659466205111867109614573242316954383604389464524535467759401326264883566523043560811873179996072188155290081861628010250468430411854935707396605833540921031884571521279145124581094374547412403086564118143957940727734634769439112260383017302489106932716079961487372942529947238400000000000000000000000000000000000000000000000000000000
232!=415798210832770977015571637026261943061848522604312624113370066788694260962277358924812122018540899189453160012306216996159585953169430580992217533416996218355769692228520181107693452987433346106108354577759088747652027298991897698378108675855550345084116012553381493679397220592936761668902813894894999677516082875409398242248834435266509874044408860014177472808390130551065070522666947759308800000000000000000000000000000000000000000000000000000000
233!=96880983124035637644628191427119032733410705766804841418415225561765762804210624629481224430320029511142586282867348560105183527088477325371186685286160118876894338289245202198092574546071969642723246616617867678202922360665112163722099321474343230404599030924937888027299552398154265468854355637510534924861247309970389790443978423417096800652347264383303351164354900418398161431781398827918950400000000000000000000000000000000000000000000000000000000
234!=22670150051024339208842996793945853659618105149432332891909162781453188496185286163298606516694886905607365190190959563064612945338703694136857684356961467817193275159683377314353662443780840896397239708288581036699483832395636246310971241224996315914676173236435465798388095261168098119711919219177465172417531870533071210963890951079600651352649259865692984172459046697905169775036847325733034393600000000000000000000000000000000000000000000000000000000
235!=5327485261990719714078104246577275610010254710116598229598653253641499296603542248375172531423298422817730819694875497320184042154595368122161555823885944937040419662525593668873110674288497610653351331447816543624378700612974517883078241687874134239948900710562334462621202386374503058132301016506704315518119989575271734576514373503706153067872576068437851280527875974007714897133659121547263082496000000000000000000000000000000000000000000000000000000000
236!=1257286521829809852522432602192237043962420111587517182185282167859393833998435970616540717415898427784984473447990617367563433948484506876830127174437083005141539040356040105854054119132085436114190914221684704295353373344661986220406465038338295680627940567692710933178603763184382721719223039895582218462276317539764129360057392146874652124017927952151332902204578729865820715723543552685154087469056000000000000000000000000000000000000000000000000000000000
237!=297976905673664935047816526719560179419093566446241572177911873782676338657629325036120150027567927385041320207173776316112533845790828129808740140341588672218544752564381505087410826234304248359063246670539274917998749482684890734236332214086176076308821914543172491163329091874698705047455860455252985775559487256924098658333601938809292553392248924659865897822485158978199509626479821986381518730166272000000000000000000000000000000000000000000000000000000000
238!=70918503550332254541380333359255322701744268814205494178343025960276968600515779358596595706561166717639834209307358763234783055298217094894480153401298103988013651110322798210803776643764411109457052707588347430483702376879003994748247066952509906161499615661275052896872323866178291801294494788350210614583157967147935480683397261436611627707355244069048083681751467836811483291102197632758801457779572736000000000000000000000000000000000000000000000000000000000
239!=16949522348529408835389899672862022125716880246595113108623983204506195495523271266704586373868118845515920376024458744413113150216273885679780756662910246853135262615367148772382102617859694255160235597113615035885604868074081954744831049001649867572598408143044737642352485404016611740509384254415700336885374754148356579883331945483350179022057903332502491999938600812997944506573425234229353548409317883904000000000000000000000000000000000000000000000000000000000
240!=4067885363647058120493575921486885310172051259182827146069755969081486918925585104009100729728348522923820890245870098659147156051905732563147381599098459244752463027688115705371704628286326621238456543307267608612545168337779669138759451760395968217423617954330737034164596496963986817722252221059768080852489940995605579171999666916004042965293896799800598079985264195119506681577622056215044851618236292136960000000000000000000000000000000000000000000000000000000000
241!=980360372638941007038951797078339359751464353463061342202811188548638347461066010066193275864531994024640834549254693776854464608509281547718518965382728677985343589672835884994580815417004715718468026937051493675623385569404900262441027874255428340399091926993707625233667755768320823071062785275404107485450075779940944580451919726756974354635829128751944137276448671023801110260206915547825809239994946405007360000000000000000000000000000000000000000000000000000000000
242!=237247210178623723703426334892958125059854373538060844813080307628770480085577974436018772759216742553963081960919635893998780435259246134547881589622620340072453148700826284168688557330915141203869262518766461469500859307795985863510728745569813658376580246332477245306547596895933639183197194036647794011478918338745708588469364573875187793821870649157970481220900578387759868682970073562573845836078777030011781120000000000000000000000000000000000000000000000000000000000
243!=57651072073405564859932599378988824389544612769748785289578514753791226660795447787952561780489668440613028916503471522241703645767996810695135226278296742637606115134300787052991319431412379312540230792060250137088708811794424564833107085173464718985508999858791970609491066045711874321516918150905413944789377156315207186998055591451670633898714567745386826936678840548225648089961727875705444538167142818292862812160000000000000000000000000000000000000000000000000000000000
244!=14066861585910957825823554248473273151048885515818703610657157599925059305234089260260425074439479099509579055626847051426975689567391221809612995211904405203575892092769392040929881941264620552259816313262701033449644950077839593819278128782325391432464195965545240828715820115153697334450128028820921002528608026140910553627525564314207634671286354529874385772549637093767058133950661601672128467312782847663458526167040000000000000000000000000000000000000000000000000000000000
245!=3446381088548184667326770790875951922006976951375582384611003611981639529782351868763804143237672379379846868628577527599609043944010849343355183826916579274876093562728501050027821075609832035303654996749361753195163012769070700485723141551669720900953728011558584003035375928212655846940281367061125645619508966404523085638743763256980870494465156859819224514274661087972929242817912092409671474491631797677547338910924800000000000000000000000000000000000000000000000000000000000
246!=847809747782853428162385614555484172813716330038393266614306888547483324326458559715895819236467405327442329682630071789503824810226668938465375221421478501619519016431211258306843984600018680684699129200342991286010101141191392319487892821710751341634617090843411664746702478340313338347309216297036908822399205735512679067130965761217294141638428587515529230511566627641340593733206374732779182724941422228676645372087500800000000000000000000000000000000000000000000000000000000000
247!=209409007702364796756109246795204590684987933519483136853733801471228381108635264249826267351407449115878255431609627732007444728125987227800947679691105189900021197058509180801790464196204614129120684912484718847644494981874273902913509526962555581383750421438322681192435512150057394571785376425368116479132603816671631729581348543020671652984691861116335719936356957027411126652101974558996458133060531290483131406905612697600000000000000000000000000000000000000000000000000000000000
248!=51933433910186469595515093205210738489877007512831817939725982764864638514941545533956914303149047380737807347039187677537846292575244832494635024563394087095205256870510276838844035120658744304021929858296210274215834755504819927922550362686713784183170104516704024935724007013214233853802773353491292886824885746534564668936174438669126569940203581556851258544216525342797959409721289690631121616999011760039816588912591949004800000000000000000000000000000000000000000000000000000000000
249!=12931425043636430929283258208097473883979374870695122666991769708451294990220444837955271661484112797803714029412757731706923726851235963291164121116285127686706108960757058932872164745044027331701460534715756358279742854120700162052715040308991732261609356024659302208995277746290344229596890565019331928819396550887106602565107435228612515915110691807655963377509914810356691893020601132967149282632753928249914330639235395302195200000000000000000000000000000000000000000000000000000000000
250!=3232856260909107732320814552024368470994843717673780666747942427112823747555111209488817915371028199450928507353189432926730931712808990822791030279071281921676527240189264733218041186261006832925365133678939089569935713530175040513178760077247933065402339006164825552248819436572586057399222641254832982204849137721776650641276858807153128978777672951913990844377478702589172973255150283241787320658188482062478582659808848825548800000000000000000000000000000000000000000000000000000000000000
251!=811446921488186040812524452558116486219705773136118947353733549205318760636332913581693296758128078062183055345650547664609463859915056696520548600046891762340808337287505448037728337751512715064266648553413711482053864096073935168807868779389231199415987090547371213614453678579719100407204882954963078533417133568165939310960491560595435373673195910930411701938747154349882416287042721093688617485205308997682124247612021055212748800000000000000000000000000000000000000000000000000000000000000
252!=204484624215022882284756162044645354527365854830301974733140854399740327680355894222586710783048275671670129947103938011481584892698594287523178247211816724109883700996451372905507541113381204196195195435460255293477573752210631662539582932406086262252828746817937545830842327002089213302615630504650695790421117659177816706362043873270049714165645369554463748888564282896170368904334765715609531606271737867415895310398229305913612697600000000000000000000000000000000000000000000000000000000000000
253!=51734609926400789218043308997295274695423561272066399607484636163134302903130041238314437828111213744932542876617296316904840977852744354743364096544589631199800576352102197345093407901685444661637384445171444589249826159309289810622514481898739824349965672944938199095203108731528570965561754517676626034976542767771987626709597099937322577683908278497279328468806763572731103332796695726049211496386749680456221513530752014396144012492800000000000000000000000000000000000000000000000000000000000000
254!=13140590921305800461383000485312999772637584563104865500301097585436112937395030474531867208340248291212865890660793264493829608374597066104814480522325766324749346393433958125653725607028102944055895649073546925669455844464559611898118678402279915384891280928014302570181589617808257025252685647489863012884041863014084857184237663384079934731712702738308949431076917947473700246530360714416499720082234418835880264436811011656620579173171200000000000000000000000000000000000000000000000000000000000000
255!=3350850684932979117652665123754814942022584063591740702576779884286208799035732771005626138126763314259280802118502282445926550135522251856727692533193070412811083330325659322041700029792166250734253390513754466045711240338462701034020262992581378423147276636643647155396305352541105541439434840109915068285430675068591638581980604162940383356586739198268782104924614076605793562865241982176207428620969776803149467431386807972438247689158656000000000000000000000000000000000000000000000000000000000000000
Таблица факториалов натуральных чисел n от 1 до 100 Факториал натурального числа n (обозначение – “n! “) равен произведению всех натуральных чисел от 1 до n включительно.
n! = 1 * 2 * 3 * 4 … * n
Ниже представлены таблицы с факториалами чисел от 1 до 20 (точные значения) и от 21 до 100 (приближенные значения).
1. Факториалы чисел от 1 до 20 Факториал числа n Значение 1! 1 2! 2 3! 6 4! 24 5! 120 6! 720 7! 5040 8! 40320 9! 362880 10! 3628800 11! 39916800 12! 479001600 13! 6227020800 14! 87178291200 15! 1307674368000 16! 20922789888000 17! 355687428096000 18! 6402373705728000 19! 121645100408832000 20! 2432902008176640000
microexcel.
2. Факториалы чисел от 21 до 100 Факториал – это быстрорастущая функция, и начиная с определенного n значения достаточно велики. Поэтому в математических вычислениях удобнее пользоваться приближенными значениями для больших чисел.
Факториал числа n Приближенное значение 21! 5,10909 ⋅ 1019 22! 1,124 ⋅ 1021 23! 2,5852 ⋅ 1022 24! 6,20448 ⋅ 1023 25! 1,55112 ⋅ 1025 26! 4,03291 ⋅ 1026 27! 1,08889 ⋅ 1028 28! 3,04888 ⋅ 1029 29! 8,84176 ⋅ 1030 30! 2,65253 ⋅ 1032 31! 8,22284 ⋅ 1033 32! 2,63131 ⋅ 1035 33! 8,68332 ⋅ 1036 34! 2,95233 ⋅ 1038 35! 1,03331 ⋅ 1040 36! 3,71993 ⋅ 1041 37! 1,37638 ⋅ 1043 38! 5,23023 ⋅ 1044 39! 2,03979 ⋅ 1046 40! 8,15915 ⋅ 1047 41! 3,34525 ⋅ 1049 42! 1,40501 ⋅ 1051 43! 6,04153 ⋅ 1052 44! 2,65827 ⋅ 1054 45! 1,19622 ⋅ 1056 46! 5,50262 ⋅ 1057 47! 2,58623 ⋅ 1059 48! 1,24139 ⋅ 1061 49! 6,08282 ⋅ 1062 50! 3,04141 ⋅ 1064 51! 1,55112 ⋅ 1066 52! 8,06582 ⋅ 1067 53! 4,27488 ⋅ 1069 54! 2,30844 ⋅ 1071 55! 1,26964 ⋅ 1073 56! 7,10999 ⋅ 1074 57! 4,05269 ⋅ 1076 58! 2,35056 ⋅ 1078 59! 1,38683 ⋅ 1080 60! 8,32099 ⋅ 1081 61! 5,0758 ⋅ 1083 62! 3,147 ⋅ 1085 63! 1,98261 ⋅ 1087 64! 1,26887 ⋅ 1089 65! 8,24765 ⋅ 1090 66! 5,44345 ⋅ 1092 67! 3,64711 ⋅ 1094 68! 2,48004 ⋅ 1096 69! 1,71122 ⋅ 1098 70! 1,1979 ⋅ 10100 71! 8,5048 ⋅ 10101 72! 6,1234 ⋅ 10103 73! 4,4701 ⋅ 10105 74! 3,3079 ⋅ 10107 75! 2,4809 ⋅ 10109 76! 1,8855 ⋅ 10111 77! 1,4518 ⋅ 10113 78! 1,1324 ⋅ 10115 79! 8,9462 ⋅ 10116 80! 7,1569 ⋅ 10118 81! 5,7971 ⋅ 10120 82! 4,7536 ⋅ 10122 83! 3,9455 ⋅ 10124 84! 3,3142 ⋅ 10126 85! 2,8171 ⋅ 10128 86! 2,4227 ⋅ 10130 87! 2,1078 ⋅ 10132 88! 1,8548 ⋅ 10134 89! 1,6508 ⋅ 10136 90! 1,4857 ⋅ 10138 91! 1,352 ⋅ 10140 92! 1,2438 ⋅ 10142 93! 1,1568 ⋅ 10144 94! 1,0874 ⋅ 10146 95! 1,033 ⋅ 10148
Как найти факториал? [закрытый] зачем делать это в C, когда вы можете сделать это в Haskell:
Новичок в Haskell программист
fac n = if n == 0
then 1
else n * fac (n-1)
второкурсник Хаскелл программист, MIT
fac = (\(n) ->
(if ((==) n 0)
then 1
else ((*) n (fac ((-) n 1)))))
младший программист Haskell
fac 0 = 1
fac (n+1) = (n+1) * fac n
другой младший программист Haskell
fac 0 = 1
fac n = n * fac (n-1)
старший программист Haskell
fac n = foldr (*) 1 [1.другой старший программист Haskell
fac n = foldl (*) 1 [1..n]
еще один старший программист Haskell
-- using foldr to simulate foldl
fac n = foldr (\x g n -> g (x*n)) id [1..n] 1
Memoizing программист Haskell
facs = scanl (*) 1 [1..]
fac n = facs !! n
бессмысленно (ГМ) » очки-бесплатно» Программатор Haskell
fac = foldr (*) 1 . enumFromTo 1
итеративный программист Haskell
fac n = result (for init next done)
where init = (0,1)
next (i,m) = (i+1, m * (i+1))
done (i,_) = i==n
result (_,m) = m
for i n d = until d n i
итеративный однострочный программист Haskell
fac n = snd (until ((>n) .накопление программиста Haskell
facAcc a 0 = a
facAcc a n = facAcc (n*a) (n-1)
fac = facAcc 1
продолжение-передача программиста Haskell
facCps k 0 = k 1
facCps k n = facCps (k . (n *)) (n-1)
fac = facCps id
Бойскаут Хаскелл программист
y f = f (y f)
fac = y (\f n -> if (n==0) then 1 else n * f (n-1))
комбинаторный программист Haskell
s f g x = f x (g x)
k x y = x
b f g x = f (g x)
c f g x = f x g
y f = f (y f)
cond p f g x = if p x then f x else g x
fac = y (b (cond ((==) 0) (k 1)) (b (s (*)) (c b pred)))
список-кодирование программиста Haskell
arb = () -- "undefined" is also a good RHS, as is "arb" :)
listenc n = replicate n arb
listprj f = length .интерпретирующий программист Haskell
-- a dynamically-typed term language
data Term = Occ Var
| Use Prim
| Lit Integer
| App Term Term
| Abs Var Term
| Rec Var Term
type Var = String
type Prim = String
-- a domain of values, including functions
data Value = Num Integer
| Bool Bool
| Fun (Value -> Value)
instance Show Value where
show (Num n) = show n
show (Bool b) = show b
show (Fun _) = ""
prjFun (Fun f) = f
prjFun _ = error "bad function value"
prjNum (Num n) = n
prjNum _ = error "bad numeric value"
prjBool (Bool b) = b
prjBool _ = error "bad boolean value"
binOp inj f = Fun (\i -> (Fun (\j -> inj (f (prjNum i) (prjNum j)))))
-- environments mapping variables to values
type Env = [(Var, Value)]
getval x env = case lookup x env of
Just v -> v
Nothing -> error ("no value for " ++ x)
-- an environment-based evaluation function
eval env (Occ x) = getval x env
eval env (Use c) = getval c prims
eval env (Lit k) = Num k
eval env (App m n) = prjFun (eval env m) (eval env n)
eval env (Abs x m) = Fun (\v -> eval ((x,v) : env) m)
eval env (Rec x m) = f where f = eval ((x,f) : env) m
-- a (fixed) "environment" of language primitives
times = binOp Num (*)
minus = binOp Num (-)
equal = binOp Bool (==)
cond = Fun (\b -> Fun (\x -> Fun (\y -> if (prjBool b) then x else y)))
prims = [ ("*", times), ("-", minus), ("==", equal), ("if", cond) ]
-- a term representing factorial and a "wrapper" for evaluation
facTerm = Rec "f" (Abs "n"
(App (App (App (Use "if")
(App (App (Use "==") (Occ "n")) (Lit 0))) (Lit 1))
(App (App (Use "*") (Occ "n"))
(App (Occ "f")
(App (App (Use "-") (Occ "n")) (Lit 1))))))
fac n = prjNum (eval [] (App facTerm (Lit n)))
статический Программатор Haskell
-- static Peano constructors and numerals
data Zero
data Succ n
type One = Succ Zero
type Two = Succ One
type Three = Succ Two
type Four = Succ Three
-- dynamic representatives for static Peanos
zero = undefined :: Zero
one = undefined :: One
two = undefined :: Two
three = undefined :: Three
four = undefined :: Four
-- addition, a la Prolog
class Add a b c | a b -> c where
add :: a -> b -> c
instance Add Zero b b
instance Add a b c => Add (Succ a) b (Succ c)
-- multiplication, a la Prolog
class Mul a b c | a b -> c where
mul :: a -> b -> c
instance Mul Zero b Zero
instance (Mul a b c, Add b c d) => Mul (Succ a) b d
-- factorial, a la Prolog
class Fac a b | a -> b where
fac :: a -> b
instance Fac Zero One
instance (Fac n k, Mul (Succ n) k m) => Fac (Succ n) m
-- try, for "instance" (sorry):
--
-- :t fac four
начинающий выпускник Haskell программист
-- the natural numbers, a la Peano
data Nat = Zero | Succ Nat
-- iteration and some applications
iter z s Zero = z
iter z s (Succ n) = s (iter z s n)
plus n = iter n Succ
mult n = iter Zero (plus n)
-- primitive recursion
primrec z s Zero = z
primrec z s (Succ n) = s n (primrec z s n)
-- two versions of factorial
fac = snd .Cartesianally-склонный программист Haskell
-- (product-based, list) catamorphisms and an application
cata (n,c) [] = n
cata (n,c) (x:xs) = c (x, cata (n,c) xs)
mult = uncurry (*)
prod = cata (1, mult)
-- (co-product-based, list) anamorphisms and an application
ana f = either (const []) (cons .PH. D. Haskell программист
-- explicit type recursion based on functors
newtype Mu f = Mu (f (Mu f)) deriving Show
in x = Mu x
out (Mu x) = x
-- cata- and ana-morphisms, now for *arbitrary* (regular) base functors
cata phi = phi . fmap (cata phi) . out
ana psi = in . fmap (ana psi) . psi
-- base functor and data type for natural numbers,
-- using a curried elimination operator
data N b = Zero | Succ b deriving Show
instance Functor N where
fmap f = nelim Zero (Succ .профессор штатный
fac n = product [1..n]
ООО «ФАКТОРИАЛ-99» (ИНН: 6164070600) Любой городМоскваАбазаАбаканАбдулиноАбинскАгидельАгрызАдлерАдыгейскАзнакаевоАзовАк-довуракАксайАлагирАлапаевскАлатырьАлданАлейскАлександровАлександровскАлександровск-сахалинскийАлексеевкаАлексинАлзамайАлуштаАльметьевскАмурскАнадырьАнапаАнгарскАндреапольАнжеро-судженскАниваАпатитыАпрелевкаАпшеронскАрамильАргунАрдатовАрдонАрзамасАркадакАрмавирАрмянскАрсеньевАрскАртемАртемовскАртемовскийАрхангельскАсбестАсиноАстраханьАткарскАхтубинскАхтубинск-7АчинскАшаБабаевоБабушкинБавлыБагратионовскБайкальскБайконурБайконурБаймакБакалБаксанБалабановоБалаковоБалахнаБалашихаБалашовБалейБалтийскБарабинскБарнаулБарышБатайскБахчисарайБеднодемьяновскБежецкБелая калитваБелая холуницаБелгородБелебейБелевБелинскийБеловоБелогорскБелозерскБелокурихаБеломорскБелорецкБелореченскБелоусовоБелоярскийБелыйБердскБерезникиБерезовскийБесланБийскБикинБилибиноБиробиджанБирскБирюсинскБирючБлаговещенскБлагодарныйБобровБогдановичБогородицкБогородскБоготолБогучарБодайбоБокситогорскБолгарБологоеБолотноеБолоховоБолховБольшой каменьБорБорзяБорисоглебскБоровичиБоровскБоровск-1БородиноБорокБратскБронницыБрянскБугульмаБугурусланБуденновскБузулукБуинскБуйБуйнакскБутовоБутурлиновкаВалдайВалуйкиВелижВеликие лукиВеликие луки-1Великий новгородВеликий устюгВельскВеневВерещагиноВереяВерх-тулинский с/сВерхнеуральскВерхний тагилВерхний уфалейВерхняя пышмаВерхняя салдаВерхняя тураВерхотурьеВерхоянскВесьегонскВетлугаВидноеВилюйскВилючинскВихоревкаВичугаВладивостокВладикавказВладимирВолгоградВолгодонскВолгореченскВолжскВолжскийВологдаВолодарскВолоколамскВолосовоВолховВолчанскВольскВоркутаВоронежВоронеж-45ВорсмаВоскресенскВоткинскВсеволожскВуктылВыборгВыксаВысоковскВысоцкВытеграВышний волочекВяземскийВязникиВязьмаВятские поляныГ.
Факториал числа.
Вам могут также быть полезны следующие сервисы Калькуляторы (Комбинаторика) Калькулятор нахождения числа перестановок из n элементов Калькулятор нахождения числа сочетаний из n элементов Калькулятор нахождения числа размещений из n элементов Калькуляторы линейная алгебра и аналитическая геометрия Калькулятор сложения и вычитания матриц Калькулятор умножения матриц Калькулятор транспонирование матрицы Калькулятор нахождения определителя (детерминанта) матрицы Калькулятор нахождения обратной матрицы Длина отрезка. Онлайн калькулятор нахождения координат вектора по двум точкам Калькулятор нахождения модуля (длины) вектора Калькулятор сложения и вычитания векторов Калькулятор скалярного произведения векторов через длину и косинус угла между векторами Калькулятор скалярного произведения векторов через координаты Калькулятор векторного произведения векторов через координаты Калькулятор смешанного произведения векторов Калькулятор умножения вектора на число Калькулятор нахождения угла между векторами Калькулятор проверки коллинеарности векторов Калькулятор проверки компланарности векторов Калькуляторы систем счисления Калькулятор перевода чисел из арабских в римские и из римских в арабские Калькулятор перевода чисел в различные системы счисления Калькулятор сложения, вычитания, умножения и деления двоичных чисел Системы счисления теория N2 | Двоичная система счисления N3 | Троичная система счисления N4 | Четырехичная система счисления N5 | Пятеричная система счисления N6 | Шестеричная система счисления N7 | Семеричная система счисления N8 | Восьмеричная система счисления N9 | Девятеричная система счисления N11 | Одиннадцатиричная система счисления N12 | Двенадцатеричная система счисления N13 | Тринадцатеричная система счисления N14 | Четырнадцатеричная система счисления N15 | Пятнадцатеричная система счисления N16 | Шестнадцатеричная система счисления N17 | Семнадцатеричная система счисления N18 | Восемнадцатеричная система счисления N19 | Девятнадцатеричная система счисления N20 | Двадцатеричная система счисления N21 | Двадцатиодноричная система счисления N22 | Двадцатидвухричная система счисления N23 | Двадцатитрехричная система счисления N24 | Двадцатичетырехричная система счисления N25 | Двадцатипятеричная система счисления N26 | Двадцатишестеричная система счисления N27 | Двадцатисемеричная система счисления N28 | Двадцативосьмеричная система счисления N29 | Двадцатидевятиричная система счисления N30 | Тридцатиричная система счисления N31 | Тридцатиодноричная система счисления N32 | Тридцатидвухричная система счисления N33 | Тридцатитрехричная система счисления N34 | Тридцатичетырехричная система счисления N35 | Тридцатипятиричная система счисления N36 | Тридцатишестиричная система счисления Дроби Калькулятор интервальных повторений Учим дроби наглядно Калькулятор сокращения дробей Калькулятор преобразования неправильной дроби в смешанную Калькулятор преобразования смешанной дроби в неправильную Калькулятор сложения, вычитания, умножения и деления дробей Калькулятор возведения дроби в степень Калькулятор перевода десятичной дроби в обыкновенную Калькулятор перевода обыкновенной дроби в десятичную Калькулятор сравнения дробей Калькуляторы (тригонометрия) Калькулятор синуса угла Калькулятор косинуса угла Калькулятор тангенса угла Калькулятор котангенса угла Калькулятор секанса угла Калькулятор косеканса угла Калькулятор арксинуса угла Калькулятор арккосинуса угла Калькулятор арктангенса угла Калькулятор арккотангенса угла Калькулятор арксеканса угла Калькулятор арккосеканса угла Калькуляторы (Теория чисел) Калькулятор со скобками Калькулятор разложения числа на простые множители Калькулятор НОД и НОК Калькулятор НОД и НОК по алгоритму Евклида Представление многозначных чисел в виде суммы разрядных слагаемых Калькулятор деления числа в данном отношении Калькулятор процентов Калькулятор перевода числа с Е в десятичное Калькулятор нахождения факториала числа Калькулятор нахождения логарифма числа Калькулятор квадратных уравнений Калькулятор остатка от деления Калькулятор корней с решением Калькулятор нахождения периода десятичной дроби Калькуляторы площади геометрических фигур Площадь квадрата Площадь прямоугольника Генератор Pdf с примерами Тренажёры решения примеров Тренажер сложения Тренажёр вычитания Тренажёр умножения Тренажёр деления Тренажёр таблицы умножения Тренажер счета для дошкольников Тренажер счета на внимательность для дошкольников Тренажер решения примеров на сложение, вычитание, умножение, деление. Тренажер решения примеров с разными действиями Тренажёры решения столбиком Тренажёр сложения столбиком Тренажёр вычитания столбиком Тренажёр умножения столбиком Тренажёр деления столбиком с остатком Калькуляторы решения столбиком Калькулятор сложения, вычитания, умножения и деления столбиком Калькулятор деления столбиком с остатком Конвекторы величин Конвертер единиц длины Калькуляторы (физика) Механика
Калькулятор вычисления скорости, времени и расстояния Калькулятор вычисления ускорения, скорости и перемещения Калькулятор вычисления времени движения Калькулятор времени Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. Импульс тела. Калькулятор вычисления импульса, массы и скорости Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения Оптика
Калькулятор отражения и преломления света Электричество и магнетизм
Калькулятор Закона Ома Калькулятор Закона Кулона Калькулятор напряженности E электрического поля Калькулятор нахождения точечного электрического заряда Q Калькулятор нахождения силы F действующей на заряд q Калькулятор вычисления расстояния r от заряда q Калькулятор вычисления потенциальной энергии W заряда q Калькулятор вычисления потенциала φ электростатического поля Калькулятор вычисления электроемкости C проводника и сферы Конденсаторы
Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе Калькулятор вычисления энергии W заряженного конденсатора
Калькуляторы по астрономии Вес тела на других планетах Ускорение свободного падения на планетах Солнечной системы и их спутниках Генераторы Генератор примеров по математике Генератор случайных чисел Генератор паролей
Факториальный калькулятор n! — Онлайн факторный калькулятор
Онлайн калькуляторы> Математические калькуляторы> Факториальный калькулятор
Факториал Калькулятор вычисляет факториал числа. Онлайн факториал вычислить, чтобы вычислить n! быстро и легко.
Онлайн-факторный калькулятор Номер:
Факториальный калькулятор Результаты Факториал:
Факториальная формула Ниже приводится формула факториала , которая показывает, как вычислить факториал числа.
Например, факториал 5 равен
Номер Факториал 1 1 2 2 3 6 4 24 5 120 6 720 7 5040 8 40320 9 362880 10 3628800 11 39916800 12 47 00
13 6227020800 14 871782 15 1.307674368E + 12 16 2.0922789888E + 13 17 3,55687428096E + 14 18 6.40237370573E + 15 19 1. 20 2.432 818E + 18 21 5.101717E + 19
22 1.12400072778E + 21 23 2.58520167389E + 22 24 6.20448401733E + 23 25 1.55112100433E + 25 26 4.032 127E + 26
27 1.08888694504E + 28 28 3.04888344612E + 29 29 8.84176199374E + 30 30 2.65252859812E + 32 31 8.22283865418E + 33 32 2,63130836934E + 35 33 8.68331761881E + 36 34 2.9523279904E + 38 35 1.03331479664E + 40 36 3,7199332679E + 41 37 1,37637530912E + 43 38 5. 39 2.03978820812E + 46 40 8.15 3248E + 47 41 3.34525266132E + 49 42 1.40500611775E + 51 43 6.04152630634E + 52 44 2.65827157479E + 54 45 1.19622220865E + 56 46 5.50262215981E + 57 47 2.58623241511E + 59 48 1,2413 25E + 61
49 6.08281864034E + 62 50 3.04140932017E + 64 51 1.55111875329E + 66 52 8.06581751709E + 67 53 4,27488328406E + 69 54 2.30843697339E + 71 55 1.26964033537E + 73 56 7. 57 4.05269195049E + 76 58 2.35056133128E + 78 59 1,38683118546E + 80 60 8,32098711274E + 81 61 5.07580213877E + 83 62 3.14699732604E + 85 63 1.9826083154E + 87 64 1,26886932186E + 89 65 8,24765059208E + 90 66 5.44344939077E + 92 67 3.64711109182E + 94 68 2.48003554244E + 96 69 1.71122452428E + 98 70 1.197857167E + 100 71 8.50478588568E + 101 72 6.12344583769E + 103 73 4.47011546151E + 105 74 3. 75 2.480 114E + 109 76 1.88549470167E + 111 77 1.45183092028E + 113 78 1.13242811782E + 115 79 8.94618213078E + 116 80 7.15694570463E + 118 81 5.79712602075E + 120 82 4,75364333701E + 122 83 3.94552396972E + 124 84 3.31424013457E + 126 85 2,81710411438E + 128 86 2.42270953837E + 130 87 2.10775729838E + 132 88 1.85482642257E + 134 89 1.65079551609E + 136 90 1.48571596448E + 138 91 1.35200152768E + 140 92 1. 93 1.15677250708E + 144 94 1.08736615666E + 146 95 1.03299784882E + 148 96 9.91677934871E + 149 97 9,61927596825E + 151 98 9.4268 88E + 153
99 9,33262154439E + 155 100 9.33262154439E + 157
кратное 1
Финансовые калькуляторы
надбавок за TV
Математические калькуляторы
Калькуляторы здоровья
преобразование
в Feet 9000 MM в дюймах
Другое
Stat-Ease »v11» Руководства »Двухуровневый Factorial Введение В этом руководстве демонстрируется использование программного обеспечения Design-Expert® для двухуровневой
Примечание
Основные возможности программы : Прежде чем идти
Данные, которые вы сейчас проанализируете, взяты из учебника Дугласа Монтгомери, Design. , опубликованный John Wiley and Sons, Нью-Йорк.А
Коэффициенты и уровни для примера полного факторного расчета
При каждой комбинации этих настроек процесса экспериментаторы записывали
Примечание
Что делать, если такой фактор, как температура, трудно изменить :
Создай эксперимент Запустите программу и щелкните New Design .
Теперь вы видите четыре ветви слева от экрана. Оставайтесь с Факториалом Рандомизированный регулярный двухфакторный .
Двухуровневый конструктор факторного проектирования
Примечание
Разработчик дизайна
Design-Expert предлагает k прогонов для k ( Tips , Screen Tips ) и щелкните тему 1: « Какой тип информации ”
Давайте перейдем к делу — полнофакторному дизайну. Щелкните белый 2 4 в столбце 4 (количество факторов) в строке прогонов
Выбор полного двухуровневого дизайна по четырем факторам, что дает 16 прогонов
Нажмите кнопку Далее . Вы также можете просто дважды щелкнуть дизайн, чтобы выбрать Имя , Единицы , Низкий и Высокий уровни показаны на снимке экрана ниже.
Факторы — после ввода имени, единиц и уровней
Примечание
Как вводить буквенно-цифровые уровни : Факторов может быть два
Теперь щелкните Далее , чтобы открыть диалоговое окно «Ответы». Со стрелкой списка вы Скорость фильтрации ) галлонов / час ), как показано ниже.
Введены значения ответа
Теперь хорошо оценить силу вашего плана эксперимента.В этом случае, 10 галлонов в час 5 (изменчивость процесса). Введите эти
Мастер питания — введены необходимые вводы
Нажмите Далее , чтобы увидеть положительный результат — мощность превышает 80 процентов.
Результаты расчета мощности
Щелкните Finish , чтобы принять эти данные и создать окно макета дизайна.
Вы завершили первую фазу DOE — проектирование. Обратите внимание, что это
Примечание
Щелкните узел «Примечания», чтобы увидеть, что там написано
Примечания к файлу данных
Закройте страницу заметок, щелкнув узел «Дизайн». (Обратите внимание, что узел выглядит как
Вы поработали на этом этапе, поэтому сейчас хорошее время, чтобы сэкономить. В
Введите данные ответа На этом этапе вы обычно распечатываете рабочий лист, проводите эксперименты, Справка, учебные данные -> Скорость фильтрации .
Дважды щелкните заголовок столбца Std (на сером квадрате с надписью Std) для сортировки
Сортировка стандартным (Std) порядком
Теперь ваши данные должны соответствовать снимку экрана, показанному ниже, за исключением разных .(Проводя собственные эксперименты, всегда проводите их в случайном порядке.
Дизайн-макет в стандартном порядке — ввод данных ответа (посредством моделирования)
Примечание
Как отрегулировать ширину столбца : Обратите внимание, что заголовок столбца
Теперь, когда у вас есть записанные ответы, настало еще время сохранить
Примечание
Как изменить числовые форматы : Данные ответа пришли в Response (вверху Design Properties слева от Format , и вы увидите, что рядом с ним появится стрелка вниз. Общий . Щелкните стрелку вниз и выберите 0,0
.
Изменение формата
Используя панель свойств проекта, вы также можете изменить формат входных факторов,
Design-Expert предоставляет два метода отображения уровней факторов в
Фактические уровни факторов. Кодируется как -1 для низких уровней и +1 для высоких уровней. Формат проекта по умолчанию — это фактические уровни факторов в порядке выполнения.
Примечание
Чтобы просмотреть проект в кодированных значениях, щелкните Параметры отображения на Process Factors — Coded . Теперь ваш экран должен выглядеть
Дизайн-макет — уровни закодированных факторов (порядок выполнения может отличаться)
Обратите внимание, что узел «Дизайн» теперь отображается «закодировано» в скобках — Дизайн .Это может быть полезно, чтобы сразу увидеть, изменил ли кто-нибудь какие-либо
Теперь верните коэффициенты к их исходным значениям, щелкнув Display. в строке меню и выбор Факторы процесса — Фактический .
Предварительный анализ эффектов с помощью сортировки данных и простых точечных диаграмм Design-Expert предоставляет вам различные способы получить общее представление о ваших данных
Чтобы увидеть это, наведите указатель мыши на верхнюю часть столбца Коэффициент 1 (A: Температура)
Сортировка дизайна по коэффициенту
Теперь вы более четко увидите влияние температуры на отклик.Лучше
Посмотрите на график, как температура оказывает большое влияние на
Легенда для столбцов графика по умолчанию на данных фильтрации
Еще одним показателем сильной связи температуры со скоростью фильтрации является
Сетка корреляции — график переключения с фактора A (слева) на B (справа)
Чтобы увидеть влияние следующего фактора, B, щелкните следующий квадрат справа, как показано
Примечание
Как использовать функцию «Цвет по» : A в сравнении со скоростью фильтрации .По умолчанию Цвет по и C: Concentration , как показано ниже.
Графические столбцы зависимости температуры от скорости фильтрации, окрашенные
Вы видите, как два цвета расслаиваются на каждом уровне температуры — но
Вы можете задаться вопросом, почему на этом графике рядом с несколькими точками появляется цифра «2».
Скоро появится, и вы будете использовать мощные функции анализа в Design-Expert.
Анализируйте результаты Чтобы начать анализ проекта, щелкните узел ответа Filtration Rate на
Вкладка Transform изначально выделена, как показано ниже.
Factorial — видеоурок по C ++ Обзор
Стенограммы
Файлы упражнений
Просмотр в автономном режиме
Детали курса Функциональное программирование позволяет писать более сжатый код, который легче читать, отлаживать и поддерживать.Он вращается вокруг мощных математических функций, которые говорят компьютеру, что делать, а не как это делать. Разработчику не нужно беспокоиться о порядке выполнения, циклах или условиях. Вы просто определяете желаемый результат; обо всем остальном позаботится компьютер. Этот курс знакомит с преимуществами и функциями функционального программирования и показывает, как использовать различные методы и библиотеки в C ++, чтобы сделать код более функциональным. Инструктор Трой Майлз рассматривает встроенные функции, такие как преобразование, копирование, накопление и связывание, и показывает, как преобразовать операторы в более функциональные выражения с помощью лямбда-функций C ++.Кроме того, изучите метапрограммирование шаблонов с помощью шаблонов C ++ и библиотек STL и Boost.Hana, а также функциональное реактивное программирование с помощью библиотеки RxCpp Reactive Extensions для C ++.
Инструктор Трой Майлз
Трой Майлз — отмеченный наградами инженер-программист, спикер и автор.
Трой начал свою карьеру с написания игр на платформе 6502 и сборки x86 для ранних компьютеров, таких как Commodore 64, Apple II и IBM PC. В наши дни он пишет веб-приложения и мобильные приложения для автомобильной оценочной и информационной компании из Южной Калифорнии. Он повесил шляпу на ассемблере, но свободно владеет JavaScript, C #, C ++, Java, Kotlin и Clojure.
Узнать больше
Видеть меньше
Навыки, описанные в этом курсе Зрители этого курса Этот курс смотрели 8754 человека
Связанные курсы Факториалы 1 1 2 2 3 6 4 24 5 120 6 720 7 5040 8 40320 9 362880 10 3628800 11 39916800 12 47 00
13 6227020800 14 871782 15 1307674368000 16 20922789888000 17 35568742809612 19 121645100408832000 20 2432 8176640000 21 510171709400000
22 1124000727777610000000 23 +25852016738885000000000 24 620448401733240000000000 25 +15511210043331000000000000 26 4032 126606000000000000
27 10888869450418400000000000000 28 304888344611714000000000000000 29 8841761993739700000000000000000 30 2652528598121000000000000000
31 8222838654177920000000000000000000 32 263130836933694000000000000000000000 33 86833176188118000000000000000000 34 29523279 04000000000000000000000000
35 10333147966386100000000000000000000000000 36 371993326789 0000000000000000000000000
37 137637530 300000000000000000000000000000 38 523022617466601000000000000000000000000000000 39 20397882081197400000000000000000000000000000000 40 815 3247898000000000000000000000000000000000 41 33452526613163800000000000000000000000000000000000 42 1405006117752880000000000000000000000000000000000000 43 60415263063373800000000000000000000000000000000000000 9 0012
44 2658271574788450000000000000000000000000000000000000000 45 119622220865480000000000000000000000000000000000000000000 46 55026221598120000000000000000000000000000000000000000 47 258623241511168000000000000000000000000000000000000000000000 48 12413 2536100000000000000000000000000000000000000000000000
49 608281864034268000000000000000000000000000000000000000000000000 50 30414093201713400000000000000000000000000000000000000000000000000 51 155111875328738000000000000000000000000000000000000000000000000 52 52 8065817517094300000000000000000000000000000000000000016 74883284060020000000000000000000000000000000000000000000000000000000 54 230843697339241000000000000000000000000000000000000000000000000000000000 55 12696403353658300000000000000000000000000000000000000000000000000000000000 56 710998587804863000000000000000000000000000000000000000000000000000000000000 57 40526919504877200000000000000000000000000000000000000000000000000000000000000 58 2350561331282880000000000000000000000000000000000000000000000000000000000000000 59 1386831185456000000000000000000000000000000000000000000000000000000000000000 60 8320987112741300000000000000000000000000000000000000000000000000000000000 61 507580213877225000000000 000000000000000000000000000000000000000000000000000000000000 62 314699732603870000000000000000000000000000000000000000000000000000000000000000000 63 1982608315404440000000000000000000000000000000000000000000000000000000000000000000000000 64 126886932185884000000000000000000000000000000000000000000000000000000000000000000000000000 65 8247650592082470000000000000000000000000000000000000000000000000000000000000000000000000000 66 5443449343000000000000000000000000000000000000000000000000000000000000000000000000000000 67 36471110918188700000000000000000000000000000000000000000000000000000000000000000000000000000000 68 24800355424368300000000000000000000000000000000000000000000000000000000 0000000000000000000000 69 171122452428141000000000000000000000000000000000000000000000000000000000000000000000000000000000000 70 119785716699690000000000000000000000000000000000000000000000000000000000000000000000000000000000 71 850478588567862000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 72 61234458376886100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 73 44701154615126000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 74 3307885441519300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 75 2480 113954000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000000000000 76 1885494701666050000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 77 145183092028286000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 78 11324281178206300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 79 894618213078298000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 80 71569457046263800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 81 579712602074737000000000000000000000000000000000000000000000000000000000 0000000000000000000000000000000000000000000000000 82 475364333701284000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 83 39455239697206600000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 84 3314240134565350000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 85 281710411438055000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 86 24227095383672700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 87 2107757298379530000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 88 185482642257398000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 89 165079551600000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
90 1485715964481760000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 91 135200152767840000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 92 12438414054641300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 000000000000000000 93 1156772507081640000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 94 108736615665674000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 95 103299784882300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
96 9916779348709400000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 97 96192759682482200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 98 94268 883250000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
99 933262154439442000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 100 93326215443944200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
.
Навигация по записям

 ru
ru .n]
.n]
 fst) (\(i,m) -> (i+1, i*m)) (1,1))
fst) (\(i,m) -> (i+1, i*m)) (1,1))
 f . listenc
listprod xs ys = [ i (x,y) | x<-xs, y<-ys ]
where i _ = arb
facl [] = listenc 1
facl n@(_:pred) = listprod n (facl pred)
fac = listprj facl
f . listenc
listprod xs ys = [ i (x,y) | x<-xs, y<-ys ]
where i _ = arb
facl [] = listenc 1
facl n@(_:pred) = listprod n (facl pred)
fac = listprj facl
 iter (one, one) (\(a,b) -> (Succ a, mult a b))
fac' = primrec one (mult . Succ)
-- for convenience and testing (try e.g. "fac five")
int = iter 0 (1+)
instance Show Nat where
show = show . int
(zero : one : two : three : four : five : _) = iterate Succ Zero
Origamist Haskell programmer
(always starts out with the “basic Bird fold”)
-- (curried, list) fold and an application
fold c n [] = n
fold c n (x:xs) = c x (fold c n xs)
prod = fold (*) 1
-- (curried, boolean-based, list) unfold and an application
unfold p f g x =
if p x
then []
else f x : unfold p f g (g x)
downfrom = unfold (==0) id pred
-- hylomorphisms, as-is or "unfolded" (ouch! sorry ...)
refold c n p f g = fold c n . unfold p f g
refold' c n p f g x =
if p x
then n
else c (f x) (refold' c n p f g (g x))
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = refold (*) 1 (==0) id pred
fac'' = refold' (*) 1 (==0) id pred
iter (one, one) (\(a,b) -> (Succ a, mult a b))
fac' = primrec one (mult . Succ)
-- for convenience and testing (try e.g. "fac five")
int = iter 0 (1+)
instance Show Nat where
show = show . int
(zero : one : two : three : four : five : _) = iterate Succ Zero
Origamist Haskell programmer
(always starts out with the “basic Bird fold”)
-- (curried, list) fold and an application
fold c n [] = n
fold c n (x:xs) = c x (fold c n xs)
prod = fold (*) 1
-- (curried, boolean-based, list) unfold and an application
unfold p f g x =
if p x
then []
else f x : unfold p f g (g x)
downfrom = unfold (==0) id pred
-- hylomorphisms, as-is or "unfolded" (ouch! sorry ...)
refold c n p f g = fold c n . unfold p f g
refold' c n p f g x =
if p x
then n
else c (f x) (refold' c n p f g (g x))
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = refold (*) 1 (==0) id pred
fac'' = refold' (*) 1 (==0) id pred
 pair (id, ana f)) . f
cons = uncurry (:)
downfrom = ana uncount
uncount 0 = Left ()
uncount n = Right (n, n-1)
-- two variations on list hylomorphisms
hylo f g = cata g . ana f
hylo' f (n,c) = either (const n) (c . pair (id, hylo' f (c,n))) . f
pair (f,g) (x,y) = (f x, g y)
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = hylo uncount (1, mult)
fac'' = hylo' uncount (1, mult)
pair (id, ana f)) . f
cons = uncurry (:)
downfrom = ana uncount
uncount 0 = Left ()
uncount n = Right (n, n-1)
-- two variations on list hylomorphisms
hylo f g = cata g . ana f
hylo' f (n,c) = either (const n) (c . pair (id, hylo' f (c,n))) . f
pair (f,g) (x,y) = (f x, g y)
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = hylo uncount (1, mult)
fac'' = hylo' uncount (1, mult)
 f)
nelim z s Zero = z
nelim z s (Succ n) = s n
type Nat = Mu N
-- conversion to internal numbers, conveniences and applications
int = cata (nelim 0 (1+))
instance Show Nat where
show = show . int
zero = in Zero
suck = in . Succ -- pardon my "French" (Prelude conflict)
plus n = cata (nelim n suck )
mult n = cata (nelim zero (plus n))
-- base functor and data type for lists
data L a b = Nil | Cons a b deriving Show
instance Functor (L a) where
fmap f = lelim Nil (\a b -> Cons a (f b))
lelim n c Nil = n
lelim n c (Cons a b) = c a b
type List a = Mu (L a)
-- conversion to internal lists, conveniences and applications
list = cata (lelim [] (:))
instance Show a => Show (List a) where
show = show . list
prod = cata (lelim (suck zero) mult)
upto = ana (nelim Nil (diag (Cons . suck)) . out)
diag f x = f x x
fac = prod . upto
Post-doc Haskell programmer
(from Uustalu, Vene and Pardo’s “Recursion Schemes from Comonads” [4])
-- explicit type recursion with functors and catamorphisms
newtype Mu f = In (f (Mu f))
unIn (In x) = x
cata phi = phi .
f)
nelim z s Zero = z
nelim z s (Succ n) = s n
type Nat = Mu N
-- conversion to internal numbers, conveniences and applications
int = cata (nelim 0 (1+))
instance Show Nat where
show = show . int
zero = in Zero
suck = in . Succ -- pardon my "French" (Prelude conflict)
plus n = cata (nelim n suck )
mult n = cata (nelim zero (plus n))
-- base functor and data type for lists
data L a b = Nil | Cons a b deriving Show
instance Functor (L a) where
fmap f = lelim Nil (\a b -> Cons a (f b))
lelim n c Nil = n
lelim n c (Cons a b) = c a b
type List a = Mu (L a)
-- conversion to internal lists, conveniences and applications
list = cata (lelim [] (:))
instance Show a => Show (List a) where
show = show . list
prod = cata (lelim (suck zero) mult)
upto = ana (nelim Nil (diag (Cons . suck)) . out)
diag f x = f x x
fac = prod . upto
Post-doc Haskell programmer
(from Uustalu, Vene and Pardo’s “Recursion Schemes from Comonads” [4])
-- explicit type recursion with functors and catamorphisms
newtype Mu f = In (f (Mu f))
unIn (In x) = x
cata phi = phi . fmap (cata phi) . unIn
-- base functor and data type for natural numbers,
-- using locally-defined "eliminators"
data N c = Z | S c
instance Functor N where
fmap g Z = Z
fmap g (S x) = S (g x)
type Nat = Mu N
zero = In Z
suck n = In (S n)
add m = cata phi where
phi Z = m
phi (S f) = suck f
mult m = cata phi where
phi Z = zero
phi (S f) = add m f
-- explicit products and their functorial action
data Prod e c = Pair c e
outl (Pair x y) = x
outr (Pair x y) = y
fork f g x = Pair (f x) (g x)
instance Functor (Prod e) where
fmap g = fork (g . outl) outr
-- comonads, the categorical "opposite" of monads
class Functor n => Comonad n where
extr :: n a -> a
dupl :: n a -> n (n a)
instance Comonad (Prod e) where
extr = outl
dupl = fork id outr
-- generalized catamorphisms, zygomorphisms and paramorphisms
gcata :: (Functor f, Comonad n) =>
(forall a. f (n a) -> n (f a))
-> (f (n c) -> c) -> Mu f -> c
gcata dist phi = extr .
fmap (cata phi) . unIn
-- base functor and data type for natural numbers,
-- using locally-defined "eliminators"
data N c = Z | S c
instance Functor N where
fmap g Z = Z
fmap g (S x) = S (g x)
type Nat = Mu N
zero = In Z
suck n = In (S n)
add m = cata phi where
phi Z = m
phi (S f) = suck f
mult m = cata phi where
phi Z = zero
phi (S f) = add m f
-- explicit products and their functorial action
data Prod e c = Pair c e
outl (Pair x y) = x
outr (Pair x y) = y
fork f g x = Pair (f x) (g x)
instance Functor (Prod e) where
fmap g = fork (g . outl) outr
-- comonads, the categorical "opposite" of monads
class Functor n => Comonad n where
extr :: n a -> a
dupl :: n a -> n (n a)
instance Comonad (Prod e) where
extr = outl
dupl = fork id outr
-- generalized catamorphisms, zygomorphisms and paramorphisms
gcata :: (Functor f, Comonad n) =>
(forall a. f (n a) -> n (f a))
-> (f (n c) -> c) -> Mu f -> c
gcata dist phi = extr . cata (fmap phi . dist . fmap dupl)
zygo chi = gcata (fork (fmap outl) (chi . fmap outr))
para :: Functor f => (f (Prod (Mu f) c) -> c) -> Mu f -> c
para = zygo In
-- factorial, the *hard* way!
fac = para phi where
phi Z = suck zero
phi (S (Pair f n)) = mult f (suck n)
-- for convenience and testing
int = cata phi where
phi Z = 0
phi (S f) = 1 + f
instance Show (Mu N) where
show = show . int
cata (fmap phi . dist . fmap dupl)
zygo chi = gcata (fork (fmap outl) (chi . fmap outr))
para :: Functor f => (f (Prod (Mu f) c) -> c) -> Mu f -> c
para = zygo In
-- factorial, the *hard* way!
fac = para phi where
phi Z = suck zero
phi (S (Pair f n)) = mult f (suck n)
-- for convenience and testing
int = cata phi where
phi Z = 0
phi (S f) = 1 + f
instance Show (Mu N) where
show = show . int
 зеленоградГаврилов посадГаврилов-ямГагаринГаджиевоГайГаличГатчинаГвардейскГдовГеленджикГеоргиевскГлазовГолицыноГорбатовГорно-алтайскГорнозаводскГорнякГородецГородищеГородовиковскГородское поселение апрелевкаГородской округ черноголовкаГороховецГорькийГорячий ключГрайворонГремячинскГрозныйГрязиГрязовецГубахаГубкинГубкинскийГудермесГуковоГулькевичиГурьевскГусевГусиноозерскГусь-хрустальныйДавлекановоДагестанские огниДалматовоДальнегорскДальнереченскДаниловДанковДегтярскДедовскДемидовДербентДесногорскДжанкойДзержинскДзержинскийДивногорскДигораДимитровградДмитриевДмитриев-льговскийДмитровДмитровскДмитровск-орловскийДноДобрянкаДолгопрудныйДолинскДомодедовоДонецкДонскойДорогобужДрезнаДубнаДубовкаДудинкаДуховщинаДюртюлиДятьковоЕвпаторияЕгорьевскЕйскЕкатеринбургЕлабугаЕлецЕлизовоЕльняЕманжелинскЕмваЕнисейскЕрмолиноЕршовЕссентукиЕфремовЖелезноводскЖелезногорскЖелезногорск-илимскийЖелезнодорожныйЖердевкаЖигулевскЖиздраЖирновскЖуковЖуковкаЖуковскийЗавитинскЗаводоуковскЗаволжскЗаволжьеЗадонскЗаинскЗакаменскЗаозерныйЗаозерскЗападная двинаЗаполярныйЗарайскЗаречныйЗаринскЗвениговоЗвенигородЗверевоЗеленогорскЗеленоградЗеленоградскЗеленодольскЗеленокумскЗерноградЗеяЗимаЗлатоустЗлынкаЗмеиногорскЗнаменскЗубцовЗуевкаИвангородИвановоИвантеевкаИвдельИгаркаИжевскИзбербашИзобильныйИланскийИнзаИнкерманИннополисИнсарИнтаИпатовоИрбитИркутскИркутск-45ИсилькульИскитимИстраИстра-1Истра-2ИшимИшимбайЙошкар-олаКадниковКазаньКайерканКалачКалач-на-донуКалачинскКалининКалининградКалининскКалтанКалугаКалязинКамбаркаКаменкаКаменногорскКаменск-уральскийКаменск-шахтинскийКамень-на-обиКамешковоКамызякКамышинКамышловКанашКандалакшаКанскКарабановоКарабашКарабулакКарасукКарачаевскКарачевКаргатКаргопольКарпинскКарталыКасимовКаслиКаспийскКатав-ивановскКатайскКачканарКашинКашираКедровыйКемеровоКемьКерчьКизелКизилюртКизлярКимовскКимрыКингисеппКинельКинешмаКиреевскКиренскКиржачКирилловКиришиКировКировградКирово-чепецкКировскКирсКирсановКиселевскКисловодскКлимовскКлинКлинцыКлючиКлючи-1КнягининоКовдорКовровКовылкиноКогалымКодинскКозельскКозловкаКозьмодемьянскКолаКологривКоломнаКолпашевоКолпиноКольчугиноКоммунарКомсомольскКомсомольск-на-амуреКонаковоКондопогаКондровоКонстантиновскКопейскКораблиноКореновскКоркиноКоролевКорочаКорсаковКоряжмаКостеревоКостомукшаКостромаКотельникиКотельниковоКотельничКотласКотовоКотовскКохмаКрасавиноКрасноармейскКрасновишерскКрасногорскКраснодарКрасное селоКраснозаводскКраснознаменскКраснокаменскКраснокамскКрасноперекопскКраснослободскКраснотурьинскКрасноуральскКрасноуфимскКрасноярскКрасный кутКрасный сулинКрасный холмКременкиКронштадтКропоткинКрымскКстовоКубинкаКувандыкКувшиновоКудровоКудымкарКузнецкКуйбышевКукморКулебакиКумертауКунгурКупиноКурганКурганинскКурильскКурловоКуровскоеКурскКуртамышКурчатовКусаКушваКызылКыштымКяхтаЛабинскЛабытнангиЛаганьЛадушкинЛаишевоЛакинскЛангепасЛахденпохьяЛебедяньЛенинградЛениногорскЛенинскЛенинск-кузнецкийЛенскЛермонтовЛеснойЛесозаводскЛесосибирскЛивныЛикино-дулевоЛипецкЛипкиЛискиЛихославльЛобняЛодейное полеЛомоносовЛосино-петровскийЛугаЛузаЛукояновЛуховицыЛысковоЛысьваЛыткариноЛьговЛюбаньЛюберцыЛюбимЛюдиновоЛянторМагаданМагасМагнитогорскМайкопМайскийМакаровМакарьевМакушиноМалая вишераМалгобекМалмыжМалоархангельскМалоярославецМамадышМамоновоМантуровоМариинскМариинский посадМарксМахачкалаМглинМегионМедвежьегорскМедногорскМедыньМежгорьеМеждуреченскМезеньМеленкиМелеузМенделеевскМензелинскМещовскМиассМикуньМиллеровоМинеральные водыМинусинскМиньярМирныйМихайловМихайловкаМихайловскМичуринскМогочаМожайскМожаскМожгаМоздокМончегорскМорозовскМоршанскМосальскМоскваМоскваМосковскийМуравленкоМурашиМурманскМуромМценскМыскиМытищиМышкинНабережные челныНавашиноНаволокиНадымНазаровоНазраньНазываевскНальчикНаримановНаро-фоминскНарткалаНарьян-марНаходкаНевельНевельскНевинномысскНевьянскНелидовоНеманНерехтаНерчинскНерюнгриНестеровНефтегорскНефтекамскНефтекумскНефтеюганскНеяНижневартовскНижнекамскНижнеудинскНижние сергиНижний ломовНижний новгородНижний тагилНижняя салдаНижняя тураНиколаевскНиколаевск-на-амуреНикольскНикольскоеНовая ладогаНовая ляляНовоалександровскНовоалтайскНовоаннинскийНововоронежНоводвинскНовозыбковНовокубанскНовокузнецкНовокуйбышевскНовомичуринскНовомосковскНовопавловскНоворжевНовороссийскНовосибирскНовосиль
зеленоградГаврилов посадГаврилов-ямГагаринГаджиевоГайГаличГатчинаГвардейскГдовГеленджикГеоргиевскГлазовГолицыноГорбатовГорно-алтайскГорнозаводскГорнякГородецГородищеГородовиковскГородское поселение апрелевкаГородской округ черноголовкаГороховецГорькийГорячий ключГрайворонГремячинскГрозныйГрязиГрязовецГубахаГубкинГубкинскийГудермесГуковоГулькевичиГурьевскГусевГусиноозерскГусь-хрустальныйДавлекановоДагестанские огниДалматовоДальнегорскДальнереченскДаниловДанковДегтярскДедовскДемидовДербентДесногорскДжанкойДзержинскДзержинскийДивногорскДигораДимитровградДмитриевДмитриев-льговскийДмитровДмитровскДмитровск-орловскийДноДобрянкаДолгопрудныйДолинскДомодедовоДонецкДонскойДорогобужДрезнаДубнаДубовкаДудинкаДуховщинаДюртюлиДятьковоЕвпаторияЕгорьевскЕйскЕкатеринбургЕлабугаЕлецЕлизовоЕльняЕманжелинскЕмваЕнисейскЕрмолиноЕршовЕссентукиЕфремовЖелезноводскЖелезногорскЖелезногорск-илимскийЖелезнодорожныйЖердевкаЖигулевскЖиздраЖирновскЖуковЖуковкаЖуковскийЗавитинскЗаводоуковскЗаволжскЗаволжьеЗадонскЗаинскЗакаменскЗаозерныйЗаозерскЗападная двинаЗаполярныйЗарайскЗаречныйЗаринскЗвениговоЗвенигородЗверевоЗеленогорскЗеленоградЗеленоградскЗеленодольскЗеленокумскЗерноградЗеяЗимаЗлатоустЗлынкаЗмеиногорскЗнаменскЗубцовЗуевкаИвангородИвановоИвантеевкаИвдельИгаркаИжевскИзбербашИзобильныйИланскийИнзаИнкерманИннополисИнсарИнтаИпатовоИрбитИркутскИркутск-45ИсилькульИскитимИстраИстра-1Истра-2ИшимИшимбайЙошкар-олаКадниковКазаньКайерканКалачКалач-на-донуКалачинскКалининКалининградКалининскКалтанКалугаКалязинКамбаркаКаменкаКаменногорскКаменск-уральскийКаменск-шахтинскийКамень-на-обиКамешковоКамызякКамышинКамышловКанашКандалакшаКанскКарабановоКарабашКарабулакКарасукКарачаевскКарачевКаргатКаргопольКарпинскКарталыКасимовКаслиКаспийскКатав-ивановскКатайскКачканарКашинКашираКедровыйКемеровоКемьКерчьКизелКизилюртКизлярКимовскКимрыКингисеппКинельКинешмаКиреевскКиренскКиржачКирилловКиришиКировКировградКирово-чепецкКировскКирсКирсановКиселевскКисловодскКлимовскКлинКлинцыКлючиКлючи-1КнягининоКовдорКовровКовылкиноКогалымКодинскКозельскКозловкаКозьмодемьянскКолаКологривКоломнаКолпашевоКолпиноКольчугиноКоммунарКомсомольскКомсомольск-на-амуреКонаковоКондопогаКондровоКонстантиновскКопейскКораблиноКореновскКоркиноКоролевКорочаКорсаковКоряжмаКостеревоКостомукшаКостромаКотельникиКотельниковоКотельничКотласКотовоКотовскКохмаКрасавиноКрасноармейскКрасновишерскКрасногорскКраснодарКрасное селоКраснозаводскКраснознаменскКраснокаменскКраснокамскКрасноперекопскКраснослободскКраснотурьинскКрасноуральскКрасноуфимскКрасноярскКрасный кутКрасный сулинКрасный холмКременкиКронштадтКропоткинКрымскКстовоКубинкаКувандыкКувшиновоКудровоКудымкарКузнецкКуйбышевКукморКулебакиКумертауКунгурКупиноКурганКурганинскКурильскКурловоКуровскоеКурскКуртамышКурчатовКусаКушваКызылКыштымКяхтаЛабинскЛабытнангиЛаганьЛадушкинЛаишевоЛакинскЛангепасЛахденпохьяЛебедяньЛенинградЛениногорскЛенинскЛенинск-кузнецкийЛенскЛермонтовЛеснойЛесозаводскЛесосибирскЛивныЛикино-дулевоЛипецкЛипкиЛискиЛихославльЛобняЛодейное полеЛомоносовЛосино-петровскийЛугаЛузаЛукояновЛуховицыЛысковоЛысьваЛыткариноЛьговЛюбаньЛюберцыЛюбимЛюдиновоЛянторМагаданМагасМагнитогорскМайкопМайскийМакаровМакарьевМакушиноМалая вишераМалгобекМалмыжМалоархангельскМалоярославецМамадышМамоновоМантуровоМариинскМариинский посадМарксМахачкалаМглинМегионМедвежьегорскМедногорскМедыньМежгорьеМеждуреченскМезеньМеленкиМелеузМенделеевскМензелинскМещовскМиассМикуньМиллеровоМинеральные водыМинусинскМиньярМирныйМихайловМихайловкаМихайловскМичуринскМогочаМожайскМожаскМожгаМоздокМончегорскМорозовскМоршанскМосальскМоскваМоскваМосковскийМуравленкоМурашиМурманскМуромМценскМыскиМытищиМышкинНабережные челныНавашиноНаволокиНадымНазаровоНазраньНазываевскНальчикНаримановНаро-фоминскНарткалаНарьян-марНаходкаНевельНевельскНевинномысскНевьянскНелидовоНеманНерехтаНерчинскНерюнгриНестеровНефтегорскНефтекамскНефтекумскНефтеюганскНеяНижневартовскНижнекамскНижнеудинскНижние сергиНижний ломовНижний новгородНижний тагилНижняя салдаНижняя тураНиколаевскНиколаевск-на-амуреНикольскНикольскоеНовая ладогаНовая ляляНовоалександровскНовоалтайскНовоаннинскийНововоронежНоводвинскНовозыбковНовокубанскНовокузнецкНовокуйбышевскНовомичуринскНовомосковскНовопавловскНоворжевНовороссийскНовосибирскНовосиль Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ.
 Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов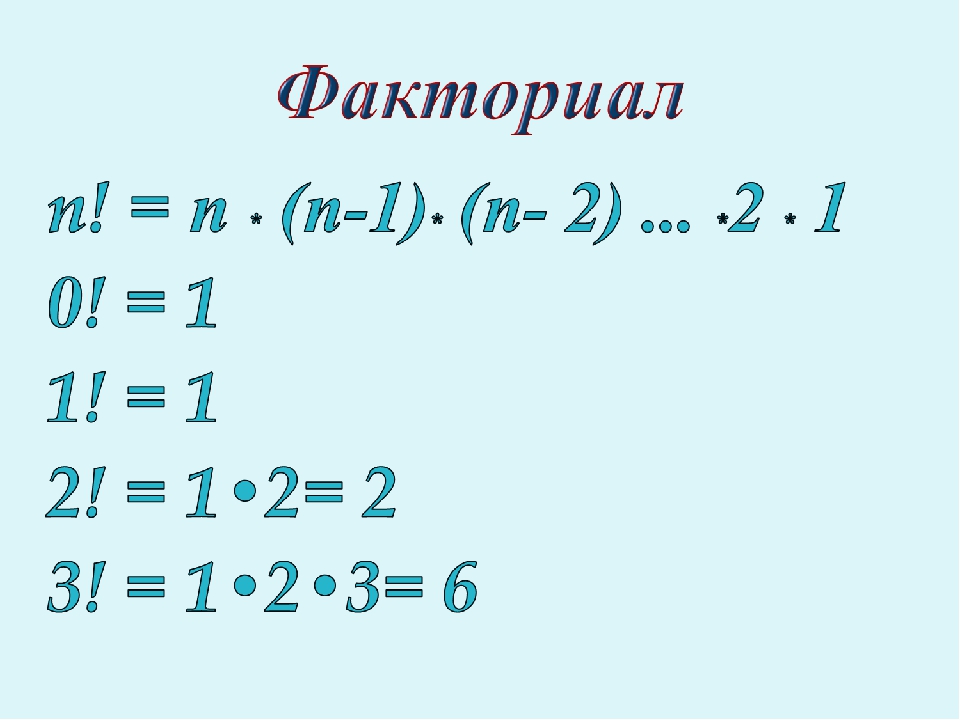 Эти дизайны помогут вам выявить множество факторов.
Эти дизайны помогут вам выявить множество факторов.
 Прежде чем приступить к разделению сюжета, пройдите «Обзорный тур», чтобы получить
Прежде чем приступить к разделению сюжета, пройдите «Обзорный тур», чтобы получить Для быстрого
Для быстрого

 Д.).
Д.).


 Например, вы можете быстро отсортировать
Например, вы можете быстро отсортировать .n]
.n]
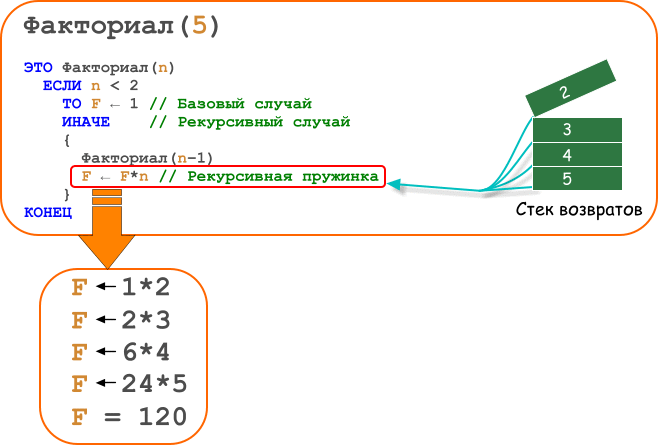 fst) (\(i,m) -> (i+1, i*m)) (1,1))
fst) (\(i,m) -> (i+1, i*m)) (1,1))
 f . listenc
listprod xs ys = [ i (x,y) | x<-xs, y<-ys ]
where i _ = arb
facl [] = listenc 1
facl n@(_:pred) = listprod n (facl pred)
fac = listprj facl
f . listenc
listprod xs ys = [ i (x,y) | x<-xs, y<-ys ]
where i _ = arb
facl [] = listenc 1
facl n@(_:pred) = listprod n (facl pred)
fac = listprj facl
 iter (one, one) (\(a,b) -> (Succ a, mult a b))
fac' = primrec one (mult . Succ)
-- for convenience and testing (try e.g. "fac five")
int = iter 0 (1+)
instance Show Nat where
show = show . int
(zero : one : two : three : four : five : _) = iterate Succ Zero
Origamist Haskell programmer
(always starts out with the “basic Bird fold”)
-- (curried, list) fold and an application
fold c n [] = n
fold c n (x:xs) = c x (fold c n xs)
prod = fold (*) 1
-- (curried, boolean-based, list) unfold and an application
unfold p f g x =
if p x
then []
else f x : unfold p f g (g x)
downfrom = unfold (==0) id pred
-- hylomorphisms, as-is or "unfolded" (ouch! sorry ...)
refold c n p f g = fold c n . unfold p f g
refold' c n p f g x =
if p x
then n
else c (f x) (refold' c n p f g (g x))
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = refold (*) 1 (==0) id pred
fac'' = refold' (*) 1 (==0) id pred
iter (one, one) (\(a,b) -> (Succ a, mult a b))
fac' = primrec one (mult . Succ)
-- for convenience and testing (try e.g. "fac five")
int = iter 0 (1+)
instance Show Nat where
show = show . int
(zero : one : two : three : four : five : _) = iterate Succ Zero
Origamist Haskell programmer
(always starts out with the “basic Bird fold”)
-- (curried, list) fold and an application
fold c n [] = n
fold c n (x:xs) = c x (fold c n xs)
prod = fold (*) 1
-- (curried, boolean-based, list) unfold and an application
unfold p f g x =
if p x
then []
else f x : unfold p f g (g x)
downfrom = unfold (==0) id pred
-- hylomorphisms, as-is or "unfolded" (ouch! sorry ...)
refold c n p f g = fold c n . unfold p f g
refold' c n p f g x =
if p x
then n
else c (f x) (refold' c n p f g (g x))
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = refold (*) 1 (==0) id pred
fac'' = refold' (*) 1 (==0) id pred
 pair (id, ana f)) . f
cons = uncurry (:)
downfrom = ana uncount
uncount 0 = Left ()
uncount n = Right (n, n-1)
-- two variations on list hylomorphisms
hylo f g = cata g . ana f
hylo' f (n,c) = either (const n) (c . pair (id, hylo' f (c,n))) . f
pair (f,g) (x,y) = (f x, g y)
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = hylo uncount (1, mult)
fac'' = hylo' uncount (1, mult)
pair (id, ana f)) . f
cons = uncurry (:)
downfrom = ana uncount
uncount 0 = Left ()
uncount n = Right (n, n-1)
-- two variations on list hylomorphisms
hylo f g = cata g . ana f
hylo' f (n,c) = either (const n) (c . pair (id, hylo' f (c,n))) . f
pair (f,g) (x,y) = (f x, g y)
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = hylo uncount (1, mult)
fac'' = hylo' uncount (1, mult)
 f)
nelim z s Zero = z
nelim z s (Succ n) = s n
type Nat = Mu N
-- conversion to internal numbers, conveniences and applications
int = cata (nelim 0 (1+))
instance Show Nat where
show = show . int
zero = in Zero
suck = in . Succ -- pardon my "French" (Prelude conflict)
plus n = cata (nelim n suck )
mult n = cata (nelim zero (plus n))
-- base functor and data type for lists
data L a b = Nil | Cons a b deriving Show
instance Functor (L a) where
fmap f = lelim Nil (\a b -> Cons a (f b))
lelim n c Nil = n
lelim n c (Cons a b) = c a b
type List a = Mu (L a)
-- conversion to internal lists, conveniences and applications
list = cata (lelim [] (:))
instance Show a => Show (List a) where
show = show . list
prod = cata (lelim (suck zero) mult)
upto = ana (nelim Nil (diag (Cons . suck)) . out)
diag f x = f x x
fac = prod . upto
Post-doc Haskell programmer
(from Uustalu, Vene and Pardo’s “Recursion Schemes from Comonads” [4])
-- explicit type recursion with functors and catamorphisms
newtype Mu f = In (f (Mu f))
unIn (In x) = x
cata phi = phi .
f)
nelim z s Zero = z
nelim z s (Succ n) = s n
type Nat = Mu N
-- conversion to internal numbers, conveniences and applications
int = cata (nelim 0 (1+))
instance Show Nat where
show = show . int
zero = in Zero
suck = in . Succ -- pardon my "French" (Prelude conflict)
plus n = cata (nelim n suck )
mult n = cata (nelim zero (plus n))
-- base functor and data type for lists
data L a b = Nil | Cons a b deriving Show
instance Functor (L a) where
fmap f = lelim Nil (\a b -> Cons a (f b))
lelim n c Nil = n
lelim n c (Cons a b) = c a b
type List a = Mu (L a)
-- conversion to internal lists, conveniences and applications
list = cata (lelim [] (:))
instance Show a => Show (List a) where
show = show . list
prod = cata (lelim (suck zero) mult)
upto = ana (nelim Nil (diag (Cons . suck)) . out)
diag f x = f x x
fac = prod . upto
Post-doc Haskell programmer
(from Uustalu, Vene and Pardo’s “Recursion Schemes from Comonads” [4])
-- explicit type recursion with functors and catamorphisms
newtype Mu f = In (f (Mu f))
unIn (In x) = x
cata phi = phi . fmap (cata phi) . unIn
-- base functor and data type for natural numbers,
-- using locally-defined "eliminators"
data N c = Z | S c
instance Functor N where
fmap g Z = Z
fmap g (S x) = S (g x)
type Nat = Mu N
zero = In Z
suck n = In (S n)
add m = cata phi where
phi Z = m
phi (S f) = suck f
mult m = cata phi where
phi Z = zero
phi (S f) = add m f
-- explicit products and their functorial action
data Prod e c = Pair c e
outl (Pair x y) = x
outr (Pair x y) = y
fork f g x = Pair (f x) (g x)
instance Functor (Prod e) where
fmap g = fork (g . outl) outr
-- comonads, the categorical "opposite" of monads
class Functor n => Comonad n where
extr :: n a -> a
dupl :: n a -> n (n a)
instance Comonad (Prod e) where
extr = outl
dupl = fork id outr
-- generalized catamorphisms, zygomorphisms and paramorphisms
gcata :: (Functor f, Comonad n) =>
(forall a. f (n a) -> n (f a))
-> (f (n c) -> c) -> Mu f -> c
gcata dist phi = extr .
fmap (cata phi) . unIn
-- base functor and data type for natural numbers,
-- using locally-defined "eliminators"
data N c = Z | S c
instance Functor N where
fmap g Z = Z
fmap g (S x) = S (g x)
type Nat = Mu N
zero = In Z
suck n = In (S n)
add m = cata phi where
phi Z = m
phi (S f) = suck f
mult m = cata phi where
phi Z = zero
phi (S f) = add m f
-- explicit products and their functorial action
data Prod e c = Pair c e
outl (Pair x y) = x
outr (Pair x y) = y
fork f g x = Pair (f x) (g x)
instance Functor (Prod e) where
fmap g = fork (g . outl) outr
-- comonads, the categorical "opposite" of monads
class Functor n => Comonad n where
extr :: n a -> a
dupl :: n a -> n (n a)
instance Comonad (Prod e) where
extr = outl
dupl = fork id outr
-- generalized catamorphisms, zygomorphisms and paramorphisms
gcata :: (Functor f, Comonad n) =>
(forall a. f (n a) -> n (f a))
-> (f (n c) -> c) -> Mu f -> c
gcata dist phi = extr . cata (fmap phi . dist . fmap dupl)
zygo chi = gcata (fork (fmap outl) (chi . fmap outr))
para :: Functor f => (f (Prod (Mu f) c) -> c) -> Mu f -> c
para = zygo In
-- factorial, the *hard* way!
fac = para phi where
phi Z = suck zero
phi (S (Pair f n)) = mult f (suck n)
-- for convenience and testing
int = cata phi where
phi Z = 0
phi (S f) = 1 + f
instance Show (Mu N) where
show = show . int
cata (fmap phi . dist . fmap dupl)
zygo chi = gcata (fork (fmap outl) (chi . fmap outr))
para :: Functor f => (f (Prod (Mu f) c) -> c) -> Mu f -> c
para = zygo In
-- factorial, the *hard* way!
fac = para phi where
phi Z = suck zero
phi (S (Pair f n)) = mult f (suck n)
-- for convenience and testing
int = cata phi where
phi Z = 0
phi (S f) = 1 + f
instance Show (Mu N) where
show = show . int
 Онлайн калькулятор
Онлайн калькулятор
 21645100409E + 17
21645100409E + 17 23022617467E + 44
23022617467E + 44 10998587805E + 74
10998587805E + 74 30788544152E + 107
30788544152E + 107 24384140546E + 142
24384140546E + 142