Матрицы в математике: Матрицы в математике: определения и применение
Матрица, ее история и применение
Матрица, её история и применение
Термин « матрица » имеет много значений. Например, в математике матрицей называется система элементов, имеющая вид прямоугольной таблицы, в программировании матрица – это двумерный массив, в электронике – набор проводников, которые можно замкнуть в точках их пересечений. Покерные фишки также имеют непосредственное отношение к матрице. Фишки для покера изготавливаются из высококачественного композиционного материала, зачастую с металлической сердцевиной. В свою очередь композиционный материал или композит имеет матрицу и включенные в нее армирующие элементы (исключение составляют слоистые композиты).
Матрица в фотографии – это интегральная микросхема (аналоговая или цифро-аналоговая), которая состоит из фотодиодов (светочувствительных элементов). Благодаря светочувствительной матрице происходит преобразование спроецированного на нее оптического изображения в электрический сигнал аналогового типа, а при наличии в составе матрицы АЦП, то преобразование происходит в поток цифровых данных.
Матрица – основной элемент цифровых фотоаппаратов, всех современных видео- и телекамер, фотокамер, встроенных в мобильный телефон и системы видеонаблюдения.
Основное значение термин «матрица» имеет в математике.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Так же, волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения ма
Матрицы. Определение, виды и основные понятия | Математика
Определение, виды и основные понятия | Математика
Определение матрицы
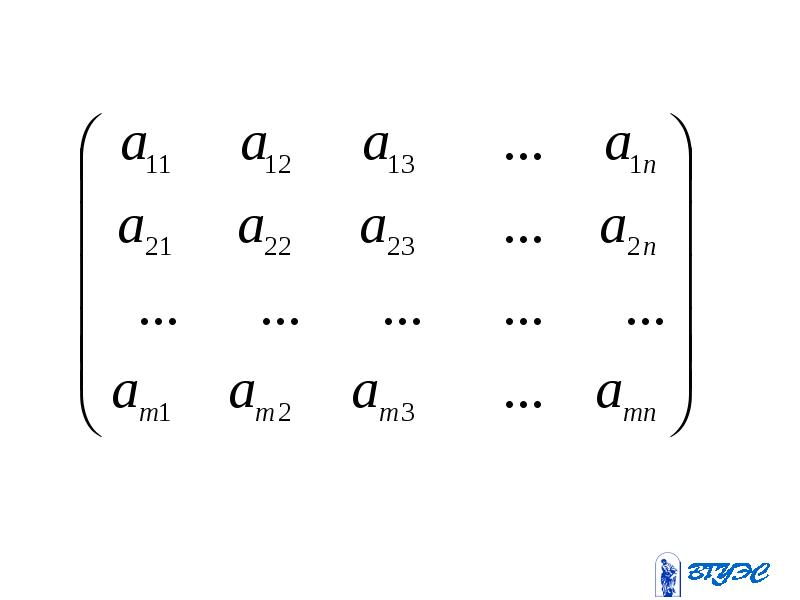
Матрицей называется прямоугольная таблица, составленная из чисел. Для обозначения матрицы применяются круглые скобки и прописные буквы А, В, С и так далее.
Например,
| (1.1) |
есть общий вид записи матрицы из чисел.
Числа составляющие матрицу, называются ее элементами.
Получить решение
Горизонтальные ряды матрицы называются строками матрицы, вертикальные — столбцами.
Индексы у элемента , где
означают, что этот элемент расположен в i-й строке и j-м столбце.
Например, элемент расположен во второй строке и в третьем столбце.
Числа и , указывающие количество строк и столбцов матрицы, называются размерами матрицы.
Наряду с обозначением (1.1) матрица обозначается также в форме:
(1. 2) 2) |
,где
Виды матриц
Матрица, у которой число строк равно числу ее столбцов называется квадратной матрицей. При этом число ее строк (столбцов) называется порядком матрицы.
Например, матрица есть квадратная матрица третьего порядка.
Квадратная матрица n-го порядка записывается в виде
| (1.3) |
В квадратной матрице (1.3) числа образуют главную диагональ матрицы, а числа побочную диагональ.
Квадратная матрица, у которой все числа, не стоящие на главной диагонали, равны нулю, называется диагональной матрицей.
Например, матрица есть диагональная матрица второго порядка.
Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Единичную матрицу обозначают прописной буквой Е.
Например, матрица есть единичная матрица второго порядка.
Матрица, состоящая только из одной строки, называется матрицей-строкой, состоящая только из одного столбца матрицей — столбцом.
Например, матрица А=(2 О 5 4) есть матрица — строка.
Матрица называется транспонированной по отношению к матрице А, если столбцы (строки) матрицы являются соответствующими строчками (столбцами) матрицы .
Например, если матрица равна
, то
Матрицы в математике, основные понятия и определения
При этом говорят, что эта матрица имеет размер .
Способы обозначения матриц
Матрицы обозначают:
Виды матриц
В зависимости от размера матрицы, вида и размещения элементов выделяют такие виды матриц:
- если число строк и столбцов в матрице совпадает и равно то такая матрица называется квадратной порядка ;
- если число строк не совпадает с числом столбцов, то матрица называется прямоугольной;
- если матрица состоит из одной строки, то её называют вектор-строка;
- если матрица состоит из одного столбца, то её называют вектор-столбец;
- матрицу размером называют скаляром;
- если все элементы квадратной матрицы, кроме элементов стоящих на главной диагонали, равны нулю, то такая матрица называется диагональной:
- диагональная матрица, у которой все элементы главной диагонали – единицы, называется единичной и обозначается буквой
- если все элементы матрицы нули, то её называют нулевой матрицей;
- квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю, называется треугольной.
 Если нули расположены ниже главной диагонали, то матрица верхнетреугольная, а если выше – нижнетреугольная.
Если нули расположены ниже главной диагонали, то матрица верхнетреугольная, а если выше – нижнетреугольная.
Равные матрицы
Две матрицы и равны, если
- обе они имеют одинаковый размер;
- их соответствующие элементы равны.
|
Понравился сайт? Расскажи друзьям! |
| ||
Матрицы — Введение
Каталин Дэвид
Матрица — это прямоугольная таблица, состоящая из строк и столбцов, содержащих числа.
Общий вид матрицы выглядит таким образом:
Элементы матрицы обозначаются $a_{n,m}$, где m — номер строки, а n — номер столбца, на пересечении которых находится данный элемент.
Пример 1
$A= \begin{pmatrix} 1 & 0 & 2\\ 3 & 1 & 4\\ \end{pmatrix} $
A — матрица из 2 строк и 3 столбцов, в которой число 2 стоит в первой строке, третьем столбце.
Пример 2
$A= \begin{pmatrix} 1 & 5 & 2\\ 8 & 7 & 3\\ \end{pmatrix} $
B — матрица из 3 строк и 2 столбцов, в которой число 8 стоит во второй строке, втором столбце.
Матрица с равным числом строк и столбцов называется квадратной матрицей.
Пример 3 $A= \begin{pmatrix} 1 & 2 & 3\\ 2 & 5 & 1\\ \end{pmatrix} $
C — матрица из 3 строк и 3 столбцов
D — общий вид квадратной матрицы.
$D= \begin{pmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3} & . & . & \color{blue}{a_{1,n}}\\ a_{2,1} & \color{red}{a_{2,2}} & a_{2,3} & . & \color{blue}{a_{2,n-1}} & a_{2,n}\\ a_{3,1} & a_{3,2} & \color{red}{a_{3, \color{blue}{3}}} & . & . & a_{3,n}\\ . & \color{blue}{a_{n-1,2}} & . {T}=\begin{pmatrix} 1 & 5\\ 3 & 9 \end{pmatrix}$
{T}=\begin{pmatrix} 1 & 5\\ 3 & 9 \end{pmatrix}$
Что такое матрицы и что с ними делать? *
Первым и, пожалуй, одним из простых понятий, встречающихся в математической науке, является матрица. В нашей статье речь пойдет не о знаменитом одноименном фильме, а о математической единице. Сегодня мы расскажем: что это такое и с чем это «есть», как применять на практике.
Что такое матрица?
Впервые с этим понятием сталкиваются студенты 1-2 курсов независимо от факультета и выбранной специальности. В общем виде матрица представляет собой прямоугольную таблицу с числами, притом каждое из них занимает определенное место и положение, имеет собственное обозначение.
Каждая матрица имеет свое имя. Оно обозначается заглавными буквами латинского алфавита: А, В, С и пр.
У каждой матрицы есть свой размер. Одежду подбирать ей не придется, но вот учитывать это параметр при действиях над матрицей нужно обязательно. Размер матрицы определяется, исходя из количества строк и столбцов, которые обозначают m и n соответственно.
Пример матрицы
Все числа, образующие таблицу (непосредственно матрицу), называют элементами матрицы. У каждого из них есть свое обозначение с учетом местоположения (строка+столбец). Например, элемент, находящийся в первой строке и первом столбце обозначают а11, а элемент в первой строке и втором столбце – а12.
Возникли сложности?
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Какие действия можно выполнять над матрицами?
Матрицы, как математическая единица, поддаются всем основным действиям: сложение, вычитание, умножение и даже деление. Каждая из операций будет иметь определенный порядок действий и потребует соблюдение конкретных условий.
Особенности сложения и вычитания матриц
Одним из важнейших требований в данном случае является соразмерность матриц. Оно означает, что размер матриц должен быть одинаковым. В противном случае сложить или вычесть один элемент из другого не удастся. При разном количестве элементов произвести необходимые действия не представляется возможным.
Сложение и вычитание соразмерных м
Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.
Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.
Матрицы (и соответственно математический раздел — матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин «матрица» появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.
Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m — строк и n — столбцов.
Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ.
Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,. .., ann .
.., ann .
Равенство матриц.
A=B, если порядки матриц A и B одинаковы и aij=bij (i=1,2,…,m; j=1,2,…,n)
Действия над матрицами.
1. Сложение матриц — поэлементная операция
2. Вычитание матриц — поэлементная операция
3. Произведение матрицы на число — поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сijматрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
Покажем операцию умножения матриц на примере
5. Возведение в степень
m>1 целое положительное число. А — квадратная матрица (m=n) т.е. актуально только для квадратных матриц
А — квадратная матрица (m=n) т.е. актуально только для квадратных матриц
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A’
Строки и столбцы поменялись местами
Пример
Свойства опрераций над матрицами
A+B=B+A
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
(A’)’=A
(λA)’=λ(A)’
(A+B)’=A’+B’
(AB)’=B’A’
Виды матриц
1. Прямоугольные: m и n — произвольные положительные целые числа
2. Квадратные: m=n
3. Матрица строка: m=1. Например, (1 3 5 7 ) — во многих практических задачах такая матрица называется вектором
4. Матрица столбец: n=1. Например
Матрица столбец: n=1. Например
5. Диагональная матрица: m=n и aij=0, если i≠j. Например
6. Единичная матрица: m=n и
7. Нулевая матрица: aij=0, i=1,2,…,m
j=1,2,…,n
8. Треугольная матрица: все элементы ниже главной диагонали равны 0.
Пример.
9. Симметрическая матрица: m=n и aij=aji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A
Например,
10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем aii=-aii)
Пример.
Ясно, A’=-A
11. Эрмитова матрица: m=n и aii=-ãii (ãji— комплексно — сопряженное к aji, т.е. если A=3+2i, то комплексно — сопряженное Ã=3-2i)
Пример
Матрица (математика) Факты для детей
Для ссылок на конкретные элементы матрицы часто используются пары нижних индексов для чисел в каждой из строк и столбцов .
В математике матрица (во множественном числе: матрицы ) представляет собой прямоугольник чисел, расположенный в строках и столбцах . Каждая строка располагается слева направо (горизонтально), а столбцы идут сверху вниз (вертикально). Левая верхняя ячейка находится в строке 1, столбце 1 (см. Диаграмму справа) .
Матрицы часто представлены заглавными латинскими буквами, такими как [math] A [/ math], [math] B [/ math] и [math] C [/ math], [1] , и существуют правила сложения , вычитание и «умножение» матриц вместе, но правила другие, чем для чисел. [2] Например, произведение [math] AB [/ math] не всегда дает тот же результат, что и [math] BA [/ math], что имеет место при умножении обычных чисел. [3] Матрица может иметь более двух измерений, например трехмерная матрица.Кроме того, матрица может быть одномерной в виде одной строки или одного столбца.
[2] Например, произведение [math] AB [/ math] не всегда дает тот же результат, что и [math] BA [/ math], что имеет место при умножении обычных чисел. [3] Матрица может иметь более двух измерений, например трехмерная матрица.Кроме того, матрица может быть одномерной в виде одной строки или одного столбца.
Многие естественные науки довольно часто используют матрицы. Во многих университетах курсы по матрицам (обычно называемые линейной алгеброй) преподаются очень рано, иногда даже на первом году обучения. Матрицы также очень распространены в информатике, инженерии, физике, экономике и статистике. [4]
Определения и обозначения
Горизонтальные линии в матрице называются строками , а вертикальные линии называются столбцами .Матрица с м строк и n столбцов называется матрицей м на n (или матрицей м × n ), а м и n называются ее размерами .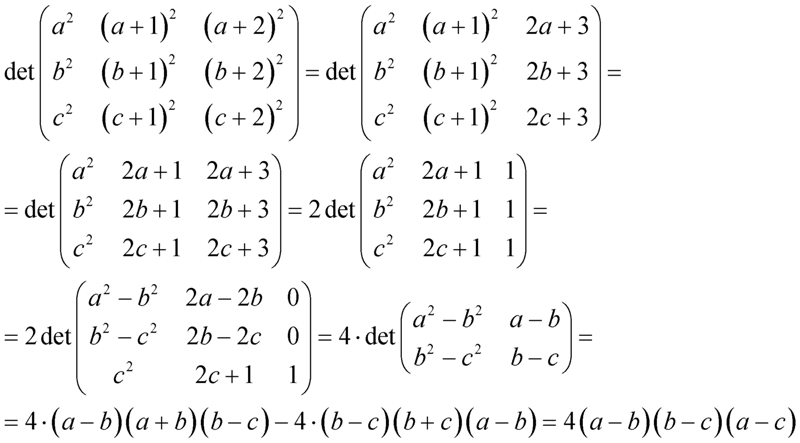
Места в матрице, где находятся числа, называются записями . [2] Запись матрицы A , которая находится в строке номер i и номер столбца j , называется записью i, j A .Это записывается как A [ i, j ] или a i, j .
Мы пишем [math] A: = (a_ {ij}) _ {m \ times n} [/ math], чтобы определить матрицу m × n A , с каждой записью в матрице, называемой a i, j для всех 1 ≤ i ≤ м и 1 ≤ j ≤ n .
Пример
Матрица
- [математика] \ begin {bmatrix}
1 и 2 и 3 \\
1 и 2 и 7 \\
4 и 9 и 2 \\
6 & 1 & 5 \ end {bmatrix} [/ math]
— это матрица 4 × 3.Эта матрица имеет m = 4 строки и n = 3 столбца.
Элемент A [2,3] или a 2,3 равен 7.
Операции
Дополнение
Основная статья: Добавление матрицы
Сумма двух матриц — это матрица, в которой ( i , j ) -я запись равна сумме ( i , j ) -й записи двух матриц:
- [математика]
\ begin {bmatrix}
1 и 3 и 2 \\
1 & 0 & 0 \\
1 и 2 и 2
\ end {bmatrix}
+
\ begin {bmatrix}
0 & 0 & 5 \\
7 и 5 и 0 \\
2 и 1 и 1
\ end {bmatrix}
знак равно
\ begin {bmatrix}
1 + 0 и 3 + 0 и 2 + 5 \\
1 + 7 & 0 + 5 & 0 + 0 \\
1 + 2 и 2 + 1 и 2 + 1
\ end {bmatrix}
знак равно
\ begin {bmatrix}
1 и 3 и 7 \\
8 и 5 и 0 \\
3 и 3 и 3
\ end {bmatrix}
[/ math]
Две матрицы имеют одинаковые размеры.Здесь [math] A + B = B + A [/ math] верно (и верно в целом для матриц одинаковых размеров).
Умножение двух матриц
Основная статья: Умножение матриц
Умножение двух матриц немного сложнее:
- [математика]
\ begin {bmatrix}
а1 и а2 \\
а3 и а4 \\
\ end {bmatrix}
\ cdot
\ begin {bmatrix}
b1 и b2 \\
b3 & b4 \\
\ end {bmatrix}
знак равно
\ begin {bmatrix}
(a1 \ cdot b1 + a2 \ cdot b3) &
(a1 \ cdot b2 + a2 \ cdot b4) \\
(a3 \ cdot b1 + a4 \ cdot b3) &
(a3 \ cdot b2 + a4 \ cdot b4) \\
\ end {bmatrix}[/ math]
Итак, с числами:
- [математика]
\ begin {bmatrix}
3 и 5 \\
1 и 4 \\
\ end {bmatrix}
\ cdot
\ begin {bmatrix}
2 и 3 \\
5 & 0 \\
\ end {bmatrix}
знак равно
\ begin {bmatrix}
(3 \ cdot 2 + 5 \ cdot 5) и
(3 \ cdot 3 + 5 \ cdot 0) \\
(1 \ cdot 2 + 4 \ cdot 5) и
(1 \ cdot 3 + 4 \ cdot 0) \\
\ end {bmatrix}
знак равно
\ begin {bmatrix}
31 и 9 \\
22 и 3 \\
\ end {bmatrix}[/ math]
- Две матрицы можно перемножать друг с другом, даже если они имеют разные размеры, при условии, что количество столбцов в первой матрице равно количеству строк во второй матрице. [3]
- Результатом умножения, называемым произведением, является другая матрица с тем же количеством строк, что и первая матрица, и тем же количеством столбцов, что и вторая матрица.
- Умножение матриц не является коммутативным, что означает, что в общем случае [math] AB \ neq BA [/ math]. [4]
- Умножение матриц является ассоциативным, что означает, что [math] (AB) C = A (BC) [/ math]. [4]
Специальные матрицы
Есть несколько специальных матриц.
Квадратная матрица
Квадратная матрица имеет такое же количество строк, как и столбцов, поэтому m = n. [5]
Пример квадратной матрицы:
- [математика] \ begin {bmatrix}
5 и -2 и 4 \\
0 и 9 и 1 \\
-7 и 6 и 8 \\
\ end {bmatrix} [/ math]
В этой матрице 3 строки и 3 столбца: m = n = 3.
Личность
Основная статья: Матрица идентичности
Каждый квадратный набор размерностей матрицы имеет специальный аналог, называемый «единичной матрицей», представленный символом [math] I [/ math]. [1] В единичной матрице нет ничего, кроме нулей, кроме главной диагонали, где все единицы. Например:
- [математика] \ begin {bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\ end {bmatrix} [/ math]
— единичная матрица. Для каждого квадратного набора измерений существует ровно , одна единичная матрица . Идентичная матрица является особенной, потому что при умножении любой матрицы на единичную матрицу результатом всегда будет исходная матрица без изменений.
Обратная матрица
Основная статья: Обратимая матрица
Обратная матрица — это матрица, которая при умножении на другую матрицу равна единичной матрице. Например:
- [математика] \ begin {bmatrix}
7 и 8 \\
6 и 7 \\
\ end {bmatrix}
\ cdot
\ begin {bmatrix}
7 & -8 \\
-6 и 7 \\
\ end {bmatrix}
знак равно
\ begin {bmatrix}
1 & 0 \\
0 и 1 \\
\ end {bmatrix} [/ math]
[math] \ begin {bmatrix}
7 & -8 \\
-6 и 7 \\
\ end {bmatrix} [/ math] является обратным
[математика] \ begin {bmatrix}
7 и 8 \\
6 и 7 \\
\ end {bmatrix} [/ math].
Формула, обратная матрице 2×2, [math] \ begin {bmatrix} x & y \\ z & v \ end {bmatrix} [/ math]:
[математика] \ left (\ frac {1} {\ det} \ right) \ begin {bmatrix} v & -y \\ -z & x \ end {bmatrix} [/ math]
Где [math] \ det [/ math] — определитель матрицы. В матрице 2×2 определитель равен:
[математика] {xv-yz} [/ математика]
Матрица с одним столбцом
Матрица, в которой много строк, но только один столбец, называется вектором-столбцом.
Детерминанты
Определитель берет квадратную матрицу и вычисляет простое число, скаляр. Чтобы понять, что означает это число, возьмите каждый столбец матрицы и нарисуйте его как вектор. Параллелограмм, нарисованный этими векторами, имеет площадь, которая является определяющей. Для всех матриц 2×2 формула очень проста:
[математика] \ det \ left (
\ begin {bmatrix}
а & б \\
CD \\
\ end {bmatrix} \ right)
= ad — bc [/ math]
Для матриц 3×3 формула более сложная:
[математика] \ det \ left (
\ begin {bmatrix}
a_1 и b_1 и c_1 \\
a_2 и b_2 и c_2 \\
a_3 & b_3 & c_3 \\
\ end {bmatrix} \ right)
= a_1 (b_2 c_3 — c_2 b_3) — a_2 (b_1 c_3 — c_1 b_3) + a_3 (b_1 c_2 — c_1 b_2) [/ математика]
Не существует простых формул для определителей больших матриц, и многие программисты изучают, как заставить компьютеры быстро находить большие детерминанты.
Свойства детерминантов
Все детерминанты подчиняются трем правилам. Это:
ATAR и масштабирование Часть 2: масштабирование меток HSC
Масштабирование меток HSC
Что подразумевается под масштабированием HSC? Второй шаг в определении вашего ATAR — это преобразование меток HSC в масштабированные метки.
После того, как ваши оценки HSC будут определены NESA, они будут отправлены в приемный центр университетов (UAC) для преобразования в масштабированные оценки. UAC преобразует ваши метки HSC в масштабированные метки с помощью процесса, называемого «масштабирование».
Давайте посмотрим, что это значит для вас. В таблице ниже показаны оценки HSC и шкалы для различных курсов ATAR. Помните, что масштабированные метки отличаются от меток HSC.
| Таблица: Масштабирование меток HSC | ||||||||
| Тема | Единицы | HSC Mark | Scaled Mark | |||||
| Английский Расширенный | 2 Английский язык Продвинутый | 2 Математика Продвинутый уровень | 2 | 94 | 86 | |||
| Бизнес-исследования | 2 | 88 | 76 | |||||
| Химия | 2 | 89 | 80 | |||||
| Расширение истории 1 | 1 | 46 | 42 | |||||
Что такое масштабирование?
Масштабирование оценок HSC — это процесс « стандартизации » исходных оценок (помните, ваша оценка HSC — это среднее значение оценки за экзамен HSC и оценочной оценки средней школы), предоставляемых NESA, а затем оценки того, какими были бы эти оценки, если бы все курсы были изучены всеми студентами.
В конце этого процесса масштабирования разные оценки по разным предметам преобразуются в единую оценку UAC (также известную как «совокупность») для каждого предмета. Хотя шкала оценок обычно отличается от исходных оценок, на основе которых они получены, рейтинг студентов в рамках курса не меняется.
Масштабирование похоже на преобразование иностранной валюты в австралийскую валюту.
Вы можете сравнить масштабирование с конвертацией иностранной валюты (HSC-марка предмета) в австралийскую валюту (масштабированная марка предмета).Поскольку к разным валютам применяются разные обменные курсы, разных коэффициента конверсии применяются к оценкам HSC разных предметов , когда они конвертируются в масштабированные оценки для сравнения.
Зачем необходимо масштабирование
Как вы сравниваете одного ученика, получившего 90 баллов по дополнительному модулю математики 2, с другим учащимся, получившим 90 баллов по углубленному направлению математики? Без масштабирования меток такое сравнение провести невозможно!
Например, в таблице ниже показано, что оценки HSC в Maths Ext 2 и Maths ADV можно справедливо сравнить только с использованием масштабированных оценок.
| Таблица: Масштабирование математики Advanced и Extension 2 | ||||||
| Subject | HSC Mark | Scaled Mark | ||||
| Mathematics Advanced | 93 | 93 | ||||
Поскольку каждый ученик изучает разную комбинацию предметов, их успеваемость по одному предмету не обязательно будет отражать их способности по разным предметам.
Одинаковые оценки на разных курсах не обязательно равны: так же, как разные валюты сравниваются с использованием обменного курса, масштабирование используется для сравнения оценок на разных курсах.
Масштабирование позволяет сравнивать оценки по «сложным» и «легким» предметам. Основополагающий принцип масштабирования состоит в том, что студент не должен ни иметь преимущества, ни ставить в невыгодное положение, выбирая один курс HSC перед другим.
Графики масштабирования для предметов HSC
Ниже представлены графики масштабирования для следующих предметов HSC:
- Курсы английского языка
- Курсы математики
- Естественные курсы
- Гуманитарные курсы
- Языковые курсы
На графике масштабирования изображены взаимосвязь между шкалой и пенсионным рангом.Вертикальная ось представляет масштабную метку, которая представляет собой оценку UAC, преобразованную из оценки HSC. Горизонтальная ось представляет процентили, которые представляют собой рейтинг студента по курсу.
Вы также можете использовать калькулятор Matrix ATAR, чтобы определить ваши оценки HSC, процентили и шкалы для каждого курса.
Курсы английского языка
График масштабирования для английского языка
График масштабирования для курсов английского языка показан ниже.
На графике масштабирования английского языка мы видим:
- Учащийся, попавший в 90-й процентиль, получит оценку по шкале:
- ESL на английском языке: 37.5/50 или 75/100
- Английский Стандартный: 27,6 / 50 или 55/100
- Английский Продвинутый: 42,5 / 50 или 85/100
- Английский Расширенный 1: 43/50
- Английский Расширенный 2: 44/50
- Учащийся, попавший в 70-й процентиль (первые 30%) по английскому продвинутому, получит ту же оценку по шкале, что и ученик из 99-го процентиля (лучший 1%) по английскому стандарту.
Insights from English Scaling Graph
Если вы можете пройти углубленный английский в качестве одного из ваших курсов ATAR, то вам следует избегать изучения стандартного английского языка, так как этот предмет плохо масштабируется.
Если вы хорошо владеете английским языком, выберите Advanced или Extension English
Английский язык является единственным обязательным предметом, и поэтому при определении вашего ATAR учитываются две ваши лучшие единицы английского языка. Поэтому английский играет важную роль в определении того, получите ли вы хороший ATAR или исключительный ATAR.
Наверх
Курсы математики
График масштабирования для математики
График масштабирования для курсов математики показан ниже.
На графике масштабирования математики мы видим:
- Учащийся, попавший в 90-й процентиль, получит оценку по шкале:
- Общая математика: 35/50 или 70/100
- Математика продвинутый: 42/50 или 84 / 100
- Расширение 1 по математике: 47/50 или 94/100
- Расширение 2 по математике: 48/50 или 98/100
- Учащийся, находящийся в 70-м процентиле (первые 30%) по дополнительному направлению 1 по математике, получит такая же шкала, как и у учащегося, занявшего 99 место.9-й процентиль (верхние 0,1%) по общей математике.
Масштабный график математики
Если вы способный студент-математик и выбираете между расширением 1 и расширением 2 по математике, вам все равно следует пройти Расширение 2 по математике.
Если вы хорошо разбираетесь в математике, рассмотрите дополнительный 1 или 2 экстренный курс по математике.
Математика Расширения 1 и 2 очень хорошо масштабируются. Учащийся по математике 1 и 2 должен быть ранжирован в 76-й процентиль (лучшие 24%) и 52-й процентиль (лучшие 48%), чтобы получить оценку по шкале 45/50 или 90/100, тогда как ученику математического продвинутого уровня потребуется быть в 98-м процентиле (верхние 2%) и получить такую же оценку по шкале.
Если вы выберете общую математику, вы должны получить ее.
Наверх
Естественные курсы
Графики масштабирования для естественных наук
График масштабирования для курсов естественных наук показан ниже.
На графике шкалы естественных наук мы видим:
- Учащийся с 90-м процентилем получит оценку по шкале:
- Биология: 39/50 или 78/100
- Химия: 41/50 или 82/100
- Физика: 40/50 или 80/100
- Старшая наука: 33/50 или 66/100
- Студент, занявший 70-й процентиль (лучшие 30%) по химии, получит такую же оценку по шкале, как и студент входит в 97-й процентиль (3% лучших) по науке для старших классов.
Масштабный график Insights from Science
Химия и физика немного лучше, чем биология.
Если вы хорошо разбираетесь в науке, предпочтите химию и физику или биологию.
Таким образом, студенты-биологи должны иметь более высокий рейтинг, чтобы получить такую же оценку по шкале, как студенты-физики и химики.
Наверх
Гуманитарные курсы
Графики масштабирования для гуманитарных наук
Графики масштабирования для гуманитарных курсов показаны ниже.
Анализ графов для гуманитарных наук
Экономика масштабируется лучше, чем бизнес-исследования или юридические исследования . Студенту-экономисту нужно только попасть в 80-й процентиль, чтобы получить оценку по шкале 40/50, тогда как студенту, изучающему бизнес, нужно будет попасть в 95-й процентиль, чтобы получить оценку 40/50.
Современная история масштабируется лучше, чем древняя история. Дополнительные предметы, такие как History Extension, всегда хорошо масштабируются.
Если вы действительно разбираетесь в музыке, подумайте о Music 2 или даже Music Extension over Music 1.
Наверх
Языковые курсы
Графики масштабирования для языков
Графики масштабирования для языковых курсов показаны ниже.
Выводы из графиков масштабирования языка
Курсы для продолжающих масштабируются лучше, чем для курсов для начинающих. Например, у японцев, продолжающих обучение, лучше весы, чем у начинающих японцев.
Если вы хорошо владеете языками, подумайте о курсе Continuers по сравнению с курсом для начинающих.
Latin Continuers и Latin Extension — лучшие курсы повышения квалификации для языков.
Вернуться к началу
Выбор правильных предметов HSC
При выборе предметов для 11 и 12 классов ученики не должны выбирать свои предметы по шкале . Однако следует использовать масштабирование для определения процентиля, необходимого для достижения желаемой оценки по шкале для каждого курса.
Студентам рекомендуется рассмотреть следующие вопросы при выборе предметов для 11 и 12 классов.
- Считаю ли я предмет интересным и / или мне он нравится? Например, считаю ли я естественные предметы более интересными, чем гуманитарные?
- Я ясно понимаю, о чем идет речь? Например, младшие науки сильно отличаются от химии, физики и биологии.
- Является ли данный предмет предварительным условием или рекомендуемым для университетского курса, которым я надеюсь заниматься в будущем? Например, если я хочу пройти медицинский курс в университете, следует ли мне рассмотреть возможность изучения и химии, и биологии?
- Я понимаю масштабирование сабжа? Выбор темы не должен зависеть только от масштабирования каждой темы. Независимо от того, насколько хорошо масштабируется объект, если вы не справляетесь с ним, масштабирование не поможет.
Хотите узнать больше о масштабировании ваших оценок HSC?
Посетите наш БЕСПЛАТНЫЙ семинар по ATAR и масштабированию, чтобы узнать, как масштабирование меток HSC влияет на ваш ATAR.Узнайте больше о нашем предстоящем семинаре по ATAR и масштабированию.
© Matrix Education и www.matrix.edu.au, 2020. Несанкционированное использование и / или копирование этого материала без явного письменного разрешения автора и / или владельца этого сайта строго запрещено. Выдержки и ссылки могут быть использованы при условии, что Matrix Education и www.matrix.edu.au полностью и четко указали на исходный контент с соответствующим конкретным указанием.
Как писать матрицы латексом? матрица, pmatrix, bmatrix, vmatrix, (…)
Прежде всего, измените преамбулу, добавив *
\ usepackage {amsmath}
* Спасибо мисс Паоле Эстрада за исправление.
LateX pmatrix, bmatrix, vmatrix, Vmatrix
pmatrix, bmatrix, vmatrix, Vmatrix — латексные среды:
- p для скоб
- b для кронштейнов
- v для вертов
- B для скоб
- V для двойных вертов.
Как написать матрицу m x n в LaTeX
\ begin {уравнение *}
A_ {m, n} =
\ begin {pmatrix}
a_ {1,1} & a_ {1,2} & \ cdots & a_ {1, n} \\
a_ {2,1} & a_ {2,2} & \ cdots & a_ {2, n} \\
\ vdots & \ vdots & \ ddots & \ vdots \\
a_ {m, 1} & a_ {m, 2} & \ cdots & a_ {m, n}
\ end {pmatrix}
\ end {уравнение *}
$$
\ begin {уравнение *}
A_ {m, n} =
\ begin {pmatrix}
a_ {1,1} & a_ {1,2} & \ cdots & a_ {1, n} \\
a_ {2,1} & a_ {2,2} & \ cdots & a_ {2, n} \\
\ vdots & \ vdots & \ ddots & \ vdots \\
a_ {m, 1} и a_ {m, 2} & \ cdots & a_ {m, n}
\ end {pmatrix}
\ end {уравнение *}
$
Примеры матрицы 3 x 3 в LaTeX
\ begin {уравнение *}
А =
\ begin {pmatrix}
1 и 2 и 3 \\
4 и 5 и 6 \\
7 и 8 и 9
\ end {pmatrix}
\ end {уравнение *}
$$
\ begin {уравнение *}
А =
\ begin {pmatrix}
1 и 2 и 3 \\
4 и 5 и 6 \\
7 и 8 и 9
\ end {pmatrix}
\ end {уравнение *}
$
\ begin {уравнение *}
В =
\ begin {bmatrix}
a & b & c \\
д & е & ф \\
g & h & i
\ end {bmatrix}
\ end {уравнение *}
$$
\ begin {уравнение *}
B =
\ begin {bmatrix}
а & b & c \\
d & e & f \\
g & h & i
\ end {bmatrix}
\ end {уравнение *}
$
Матрица LateX без кронштейна
\ begin {Equation}
\ begin {matrix}
а_ {11} и а_ {12} и а_ {13} \\
а_ {21} и а_ {22} и а_ {23} \\
а_ {31} и а_ {32} и а_ {33} \\
\ end {matrix}
\ end {Equation}
$$
\ begin {уравнение}
\ begin {matrix}
а_ {11} и а_ {12} и а_ {13} \\
а_ {21} и а_ {22} и а_ {23} \\
а_ {31} и а_ {32} и а_ {33} \\
\ end {матрица}
\ end {уравнение}
$
Определитель матрицы LateX / кронштейн для вертикальной балки
\ begin {Equation}
\ begin {vmatrix}
а_ {11} и а_ {12} и а_ {13} \\
а_ {21} и а_ {22} и а_ {23} \\
а_ {31} и а_ {32} и а_ {33} \\
\ end {vmatrix}
\ end {Equation}
$$
\ begin {уравнение}
\ begin {vmatrix}
а_ {11} и а_ {12} и а_ {13} \\
а_ {21} и а_ {22} и а_ {23} \\
а_ {31} и а_ {32} и а_ {33} \\
\ end {vmatrix}
\ end {уравнение}
$
Матрица латексная с фигурными скобками
\ begin {Equation}
\ begin {Bmatrix}
а_ {11} и а_ {12} и а_ {13} \\
а_ {21} и а_ {22} и а_ {23} \\
а_ {31} и а_ {32} и а_ {33} \\
\ end {Bmatrix}
\ end {Equation}
$$
\ begin {уравнение}
\ begin {Bmatrix}
а_ {11} и а_ {12} и а_ {13} \\
а_ {21} и а_ {22} и а_ {23} \\
а_ {31} и а_ {32} и а_ {33} \\
\ end {Bmatrix}
\ end {уравнение}
$
Латексная матрица с двойными вертикальными балками
\ begin {Equation}
\ begin {Vmatrix}
а_ {11} и а_ {12} и а_ {13} \\
а_ {21} и а_ {22} и а_ {23} \\
а_ {31} и а_ {32} и а_ {33} \\
\ end {Vmatrix}
\ end {Equation}
$$
\ begin {уравнение}
\ begin {Vmatrix}
а_ {11} и а_ {12} и а_ {13} \\
а_ {21} и а_ {22} и а_ {23} \\
а_ {31} и а_ {32} и а_ {33} \\
\ end {Vmatrix}
\ end {уравнение}
$
Малая линейная матрица из латекса
Использовать среду smallmatrix
Я люблю маленькие матрицы, такие как $ \ big (\ begin {smallmatrix} a & b \\ c & d \ end {smallmatrix} \ big) $
Я люблю маленькие матрицы, такие $ \ big (\ begin {smallmatrix} a & b \\ c & d \ end {smallmatrix} \ big) $
Примеры матрицы 2 x 2 в LaTeX
Вот примеры с матрицей 2×2 со средами pmatrix, bmatrix, vmatrix, Vmatrix:
\ begin {matrix}
а & б \\
c & d
\ end {matrix}
\ quad
\ begin {pmatrix}
а & б \\
c & d
\ end {pmatrix}
\ quad
\ begin {bmatrix}
а & б \\
c & d
\ end {bmatrix}
\ quad
\ begin {vmatrix}
а & б \\
c & d
\ end {vmatrix}
\ quad
\ begin {Vmatrix}
а & б \\
c & d
\ end {Vmatrix}
$$
\ begin {matrix}
а & б \\
CD
\ end {матрица}
\ quad
\ begin {pmatrix}
а & б \\
CD
\ end {pmatrix}
\ quad
\ begin {bmatrix}
а & б \\
CD
\ end {bmatrix}
\ quad
\ begin {vmatrix}
а & б \\
CD
\ end {vmatrix}
\ quad
\ begin {Vmatrix}
а & б \\
CD
\ end {Vmatrix}
$
Транспонирование и соединение матриц — MathsTips.com
Транспонирование матрицы
Матрица, полученная из данной матрицы A путем перестановки ее строк и столбцов, называется транспонированием матрицы A. Транспонирование матрицы A обозначается A ’или. Если A имеет порядок m * n, то A ’имеет порядок n * m. Ясно, что транспонирование транспонированной матрицы A — это сама матрица A, т.е. (A ’)’ = A.
Рассмотрим матрицу Если A = || порядка m * n, тогда = || порядка n * m. Так, .
Пример 1: Рассмотрим матрицу. Сделайте транспонирование матрицы.
Решение: Это порядок 2 * 3. Записав другую матрицу B из A, записав строки A как столбцы B. Мы имеем:. Матрица B называется транспонированной матрицей A.
Пример 2: Рассмотрим матрицу. Сделайте транспонирование матрицы.
Решение: Транспонирование матрицы A путем перестановки строк и столбцов равно.
Свойства транспонирования
- Транспонирование транспонированной матрицы состоит в том, что сама матрица = = A
- Транспонирование сложения двух матриц аналогично сумме их транспонирования =
- Когда скалярная матрица умножается на матрицу, порядок транспонирования не имеет значения =
- Транспонирование произведения матриц 2 аналогично произведению их транспонирования в обратном порядке =
Примыкание к матрице
Для квадратной матрицы A транспонированная матрица кофактора A называется присоединенной к A и обозначается adj A.Сопряженная матрица также называется сопряженной матрицей. Другими словами, мы можем сказать, что матрица A — это еще одна матрица, сформированная путем замены каждого элемента текущей матрицы его соответствующим кофактором и последующего транспонирования новой сформированной матрицы.
Предположим, тогда Adj A =
Пример 1: Рассмотрим матрицу Find the Adj of A.
Решение: Сначала нужно найти минор и сомножитель матрицы: = 2 = 2, = 2 = -2, = -1 = +1, = 5 = 5.
Матрица сомножителей = и Adj A =
Пример 2: Рассмотрим матрицу Find the Adj of A.
Решение: = 7 = 7, = 18 = -18, = 30 = 30, = 1 = -1, = 6 = 6, = 10 = -10, = 1 = 1, = 8 = -8, = 26 = 26.
Матрица сомножителей = и Adj A =.
Упражнение
- Найдите сопряженный к матрице.
- Найдите сопряженный к матрице.
- Найдите сопряженный к матрице.
- Найдите сопряженный к матрице.
 Определение, виды и основные понятия | Математика
Определение, виды и основные понятия | Математика Если нули расположены ниже главной диагонали, то матрица верхнетреугольная, а если выше – нижнетреугольная.
Если нули расположены ниже главной диагонали, то матрица верхнетреугольная, а если выше – нижнетреугольная.