Метод сжатия: Методы сжатия данных / Хабр
Форматы сжатия данных — Время электроники
В статье рассматриваются основные методы сжатия данных, приводится классификация наиболее известных алгоритмов, и на простых примерах обсуждаются механизмы работы методов CS&Q, RLE-кодирования, Хаффмана, LZW, дельта-кодирования, JPEG и MPEG. Статья представляет собой авторизованный перевод [1].
Передача данных и их хранение стоят определенных денег. Чем с большим количеством информации приходится иметь дело, тем дороже обходится ее хранение и передача. Зачастую данные хранятся в наиболее простом виде, например в коде ASCII (American Standard Code for Information Interchange — американский стандартный код для обмена информацией) текстового редактора, в исполняемом на компьютере двоичном коде, в отдельных файлах, полученных от систем сбора данных и т.д. Как правило, при использовании этих простых методов кодирования объем файлов данных примерно в два раза превышает действительно необходимый размер для представления информации.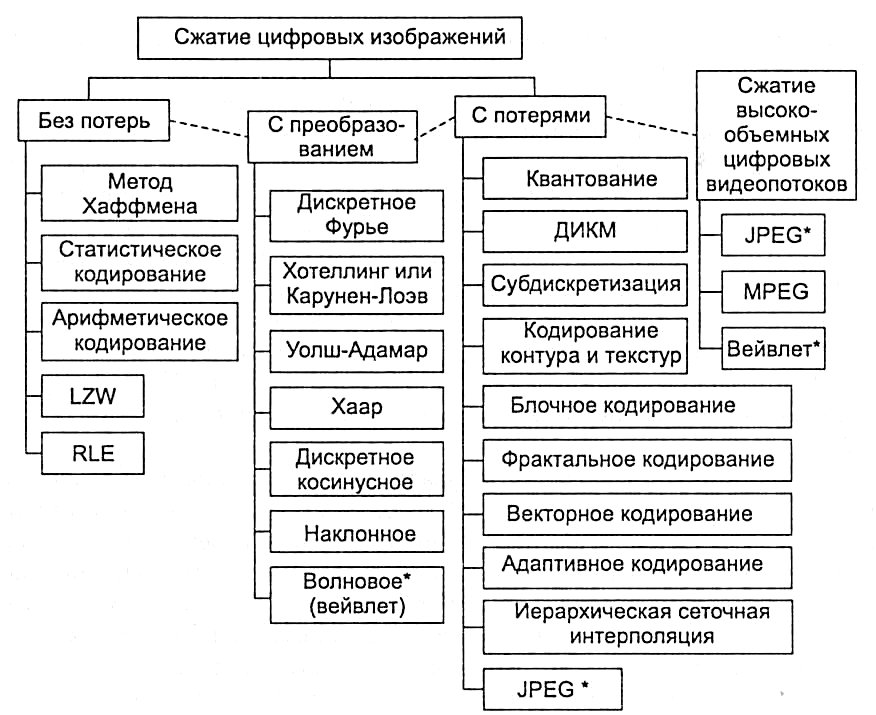 Ее сжатие с помощью алгоритмов и программ позволяет решить эту задачу. Программа сжатия используется для преобразования данных из простого формата в оптимизированный по компактности. Наоборот, программа распаковки возвращает данные в исходный вид. Мы обсудим шесть методов сжатия данных в этом разделе. Первые три из них являются простыми методами кодирования: кодирование длин серий с передачей информации об их начале и длительности; кодирование Хаффмана и дельта-кодирование. Последние три метода являются сложными процедурами сжатия данных, которые стали промышленными стандартами: LZW, форматы JPEG и MPEG.
Ее сжатие с помощью алгоритмов и программ позволяет решить эту задачу. Программа сжатия используется для преобразования данных из простого формата в оптимизированный по компактности. Наоборот, программа распаковки возвращает данные в исходный вид. Мы обсудим шесть методов сжатия данных в этом разделе. Первые три из них являются простыми методами кодирования: кодирование длин серий с передачей информации об их начале и длительности; кодирование Хаффмана и дельта-кодирование. Последние три метода являются сложными процедурами сжатия данных, которые стали промышленными стандартами: LZW, форматы JPEG и MPEG.
Методы сжатия данных
В таблице 1 показаны два разных способа распределения алгоритмов сжатия по категориям. К категории (а) относятся методы, определяемые как процедуры сжатия без потерь и с потерями. При использовании метода сжатия без потерь восстановленные данные идентичны исходным. Этот метод применяется для обработки многих типов данных, например для исполняемого кода, текстовых файлов, табличных данных и т. д. При этом не допускается потеря ни одного бита информации. В то же время файлы данных, представляющие изображения и другие полученные сигналы, нет необходимости хранить и передавать без потерь. Любой электрический сигнал содержит шум. Если изменения в этих сигналах схожи с небольшим количеством дополнительного шума, вреда не наносится. Алгоритм, применение которого приводит к некоторому ухудшение параметров сигнала, называется сжатием с потерями. Методы сжатия с потерями намного эффективнее методов кодирования без потерь. Чем выше коэффициент сжатия, тем больше шума добавляется в данные.
д. При этом не допускается потеря ни одного бита информации. В то же время файлы данных, представляющие изображения и другие полученные сигналы, нет необходимости хранить и передавать без потерь. Любой электрический сигнал содержит шум. Если изменения в этих сигналах схожи с небольшим количеством дополнительного шума, вреда не наносится. Алгоритм, применение которого приводит к некоторому ухудшение параметров сигнала, называется сжатием с потерями. Методы сжатия с потерями намного эффективнее методов кодирования без потерь. Чем выше коэффициент сжатия, тем больше шума добавляется в данные.
| Табл. 1. Классификация методов сжатия: без потерь и с потерями | ||||||||||
|
Передаваемые по интернету изображения служат наглядным примером того, почему необходимо сжатие данных. Предположим, что требуется загрузить из интернета цифровую цветную фотографию с помощью 33,6-Кбит/с модема. Если изображение не сжато (например, это файл TIFF-формата), его объем составит около 600 Кбайт. При сжатии фото без потерь (в файл GIF-формата) его размер уменьшится примерно до 300 Кбайт. Метод сжатия с потерями (JPEG-формат) позволит уменьшить размер файла до 50 Кбайт. Время загрузки этих трех файлов составляет 142, 72 и 12 с, соответственно. Это большая разница. JPEG идеально подходит для работы с цифровыми фотографиями, тогда как GIF используется только для рисованных изображений.
Предположим, что требуется загрузить из интернета цифровую цветную фотографию с помощью 33,6-Кбит/с модема. Если изображение не сжато (например, это файл TIFF-формата), его объем составит около 600 Кбайт. При сжатии фото без потерь (в файл GIF-формата) его размер уменьшится примерно до 300 Кбайт. Метод сжатия с потерями (JPEG-формат) позволит уменьшить размер файла до 50 Кбайт. Время загрузки этих трех файлов составляет 142, 72 и 12 с, соответственно. Это большая разница. JPEG идеально подходит для работы с цифровыми фотографиями, тогда как GIF используется только для рисованных изображений.
Второй способ классификации методов сжатия данных проиллюстрирован в таблице 2. Большинство программ сжатия работает с группами данных, которые берутся из исходного файла, сжимаются и записываются в выходной файл. Например, одним из таких методов является CS&Q (Coarser Sampling and Quantization — неточные выборка и дискретизация). Предположим, что сжимается цифровой сигнал, например звуковой сигнал, который оцифрован с разрядностью 12 бит. Можно прочесть две смежные выборки из исходного файла (24 бит), отбросить одну выборку полностью, отбросить наименее значащие 4 бита из другой выборки, затем записать оставшиеся 8 битов в выходной файл. При 24 входных битах и 8 выходных коэффициент сжатия алгоритма с потерями равен 3:1. Этот метод высокоэффективен при использовании сжатия с преобразованием, составляющего основу алгоритма JPEG.
Можно прочесть две смежные выборки из исходного файла (24 бит), отбросить одну выборку полностью, отбросить наименее значащие 4 бита из другой выборки, затем записать оставшиеся 8 битов в выходной файл. При 24 входных битах и 8 выходных коэффициент сжатия алгоритма с потерями равен 3:1. Этот метод высокоэффективен при использовании сжатия с преобразованием, составляющего основу алгоритма JPEG.
| Табл. 2. Классификация методов сжатия: фиксированный и переменный размер группы | |||||||||||||||||
| |||||||||||||||||
В методе CS&Q из входящего файла читается фиксированное число битов, и меньшее фиксированное число записывается в выходной файл. Другие методы сжатия позволяют создавать переменное число битов для чтения или записи. Причина того, почему в таблицу не вошли форматы JPEG и MPEG, в том, что это составные алгоритмы, в которых совмещено множество других методов.
Другие методы сжатия позволяют создавать переменное число битов для чтения или записи. Причина того, почему в таблицу не вошли форматы JPEG и MPEG, в том, что это составные алгоритмы, в которых совмещено множество других методов.
RLE-кодирование
Файлы данных содержат одни и те же символы, повторяющиеся множество раз в одном ряду. Например, в текстовых файлах используются пробелы для разделения предложений, отступы, таблицы и т.д. Цифровые сигналы также содержат одинаковые величины, указывающие на то, что сигнал не претерпевает изменений. Например, изображение ночного неба может содержать длинные серии символов, представляющих темный фон, а цифровая музыка может иметь длинную серию нулей между песнями. RLE-кодирование (Run-length encoding — кодирование по длинам серий) представляет собой метод сжатия таких типов файлов.
На рисунке 1 проиллюстрирован принцип этого кодирования для последовательности данных с частым повторением серии нулей. Всякий раз, когда нуль встречается во входных данных, в выходной файл записываются два значения: нуль, указывающий на начало кодирования, и число нулей в серии. Если среднее значение длины серии больше двух, происходит сжатие. С другой стороны, множество одиночных нулей в данных может привести к тому, что кодированный файл окажется больше исходного.
Если среднее значение длины серии больше двух, происходит сжатие. С другой стороны, множество одиночных нулей в данных может привести к тому, что кодированный файл окажется больше исходного.
Рис. 1. Пример RLE-кодирования |
Входные данные можно рассматривать и как отдельные байты, или группы, например числа с плавающей запятой. RLE-кодирование можно использовать только в случае одного знака (как в случае в нулем в примере выше), нескольких знаков или всех знаков.
Кодирование Хаффмана
Этот метод был разработан Хаффманом в 1950-х гг. Метод основан на использовании относительной частоты встречаемости индивидуальных элементов. Часто встречающиеся элементы кодируются более короткой последовательностью битов. На рисунке 2 представлена гистограмма байтовых величин большого файла ASCII. Более 96% этого файла состоит из 31 символа: букв в нижнем регистре, пробела, запятой, точки и символа возврата каретки.
Алгоритм, назначающий каждому из этих стандартных символов пятибитный двоичный код по схеме 00000 = a, 00001 = b, 00010 = c и т.д., позволяет 96% этого файла уменьшить на 5/8 объема. Последняя комбинация 11111 будет указывать на то, что передаваемый символ не входит в группу из 31 стандартного символа. Следующие восемь битов в этом файле указывают, что представляет собой символ в соотоветствии со стандартом присвоения ASCII. Итак, 4% символов во входном файле требуют для представления 5 + 8 = 13 бит.
Принцип этого алгоритма заключается в присвоении часто употребляемым символам меньшего числа битов, а редко встречающимся символам — большего количества битов. В данном примере среднее число битов, требуемых из расчета на исходный символ, равно 0,96 . 5 + 0,04 . 13 = 5,32. Другими словами, суммарный коэффициент сжатия составляет 8 бит/5,32 бит, или 1,5 : 1.
Рис. 2. Гистограмма значений ASCII фрагмента текста из этой статьи |
На рисунке 3 представлена упрощенная схема кодирования Хаффмана. В таблице кодирования указана вероятность употребления символов с A по G, имеющихся в исходной последовательности данных, и их соответствия. Коды переменной длины сортируются в стандартные восьмибитовые группы. При распаковке данных все группы выстраиваются в последовательность нулей и единиц, что позволяет разделять поток данных без помощи маркеров. Обрабатывая поток данных, программа распаковки формирует достоверный код, а затем переходит к следующему символу. Такой способ формирования кода обеспечивает однозначное чтение данных.
В таблице кодирования указана вероятность употребления символов с A по G, имеющихся в исходной последовательности данных, и их соответствия. Коды переменной длины сортируются в стандартные восьмибитовые группы. При распаковке данных все группы выстраиваются в последовательность нулей и единиц, что позволяет разделять поток данных без помощи маркеров. Обрабатывая поток данных, программа распаковки формирует достоверный код, а затем переходит к следующему символу. Такой способ формирования кода обеспечивает однозначное чтение данных.
| |||||||||||||||||||||||||
Рис. |
Дельта-кодирование
Термин «дельта-кодирование» обозначает несколько методов сохранения или передачи данных в форме разности между последующими выборками (или символами), а не сохранение самих выборок. На рисунке 4 приводится пример работы этого механизма. Первое значение в кодируемом файле является совпадает с исходным. Все последующие значения в кодируемом файле равны разности между соответствующим и предыдущим значениями входного файла.
Рис. 4. Пример дельта-кодирования |
Дельта-кодирование используется для сжатия данных, если значения исходного файла изменяются плавно, т.е. разность между следующими друг за другом величинами невелика. Это условие не выполняется для текста ASCII и исполняемого кода, но является общим случаем, когда информация поступает в виде сигнала. Например, на рисунке 5а показан фрагмент аудиосигнала, оцифрованного с разрядностью 8 бит, причем все выборки принимают значения в диапазоне –127–127. На рисунке 5б представлен кодированный вариант этого сигнала, основное отличие которого от исходного сигнала заключается в меньшей амплитуде. Другими словами, дельта-кодирование увеличивает вероятность того, что каждое значение выборки находится вблизи нуля, а вероятность того, что оно значительно больше этой величины, невелика. С неравномерным распределением вероятности работает метод Хаффмана. Если исходный сигнал не меняется или меняется линейно, в результате дельта-кодирования появятся серии выборок с одинаковыми значениями, с которыми работает RLE-алгоритм. Таким образом, в стандартном методе сжатия файлов используется дельта-кодирование с последующим применением метода Хаффмана или RLE-кодирования.
На рисунке 5б представлен кодированный вариант этого сигнала, основное отличие которого от исходного сигнала заключается в меньшей амплитуде. Другими словами, дельта-кодирование увеличивает вероятность того, что каждое значение выборки находится вблизи нуля, а вероятность того, что оно значительно больше этой величины, невелика. С неравномерным распределением вероятности работает метод Хаффмана. Если исходный сигнал не меняется или меняется линейно, в результате дельта-кодирования появятся серии выборок с одинаковыми значениями, с которыми работает RLE-алгоритм. Таким образом, в стандартном методе сжатия файлов используется дельта-кодирование с последующим применением метода Хаффмана или RLE-кодирования.
а) | б) |
Рис. 5. Пример дельта-кодирования |
Механизм дельта-кодирования можно расширить до более полного метода под названием кодирование с линейным предсказанием (Linear Predictive Coding, LPC).
Чтобы понять суть этого метода, представим, что уже были закодированы первые 99 выборок из входного сигнала и необходимо произвести выборку под номером 100. Мы задаемся вопросом о том, каково наиболее вероятное ее значение? В дельта-кодировании ответом на данный вопрос является предположение, что это значение предыдущей, 99-й выборки. Это ожидаемое значение используется как опорная величина при кодировании выборки 100. Таким образом, разность между значением выборки и ожиданием помещается в кодируемый файл. Метод LPC устанавливает наиболее вероятную величину на основе нескольких последних выборок. В используемых при этом алгоритмах применяется z-преобразование и другие математические методы.
Алгоритм LZW
LZW-сжатие — наиболее универсальный метод сжатия данных, получивший распространение благодаря своей простоте и гибкости. Этот алгоритм назван по имени его создателей (Lempel-Ziv-Welch encoding — сжатие данных методом Лемпела-Зива-Велча). Исходный метод сжатия Lempel-Ziv был впервые заявлен в 1977 г. , а усовершенствованный Велчем вариант — в 1984 г. Метод позволяет сжимать текст, исполняемый код и схожие файлы данных примерно вполовину. LZW также хорошо работает с избыточными данными, например табличными числами, компьютерным исходным текстом и принятыми сигналами. В этих случаях типичными значениями коэффициента сжатия являются 5:1. LZW-сжатие всегда используется для обработки файлов изображения в формате GIF и предлагается в качестве опции для форматов TIFF и PostScript.
, а усовершенствованный Велчем вариант — в 1984 г. Метод позволяет сжимать текст, исполняемый код и схожие файлы данных примерно вполовину. LZW также хорошо работает с избыточными данными, например табличными числами, компьютерным исходным текстом и принятыми сигналами. В этих случаях типичными значениями коэффициента сжатия являются 5:1. LZW-сжатие всегда используется для обработки файлов изображения в формате GIF и предлагается в качестве опции для форматов TIFF и PostScript.
Алгоритм LZW использует кодовую таблицу, пример которой представлен на рисунке 6. Как правило, в таблице указываются 4096 элементов. При этом кодированные LZW-данные полностью состоят из 12-битных кодов, каждый из которых соответствует одному табличному элементу. Распаковка выполняется путем извлечения каждого кода из сжатого файла и его преобразования с помощью таблицы. Табличные коды 0—255 всегда назначаются единичным байтам входного файла (стандартному набору символов). Например, если используются только эти первые 256 кодов, каждый байт исходного файла преобразуется в 12 бит сжатого LZW-файла, который на 50% больше исходного. При распаковке этот 12-битный код преобразуется с помощью кодовой таблицы в единичные байты.
При распаковке этот 12-битный код преобразуется с помощью кодовой таблицы в единичные байты.
Пример кодовой таблицы
| |||||||||||||||||||||||
Рис. 6. Пример сжатия в соответствии с таблицей кодирования |
Метод LZW сжимает данные с помощью кодов 256—4095, представляя последовательности байтов. Например, код 523 может представлять последовательность из трех байтов: 231 124 234. Всякий раз, когда алгоритм сжатия обнаруживает последовательность во входном файле, в кодируемый файл ставится код 523. При распаковке код 523 преобразуется с помощью таблицы в исходную последовательность из трех байтов. Чем длиннее последовательность, назначаемая единичному коду и чем чаще она повторяется, тем больше коэффициент сжатия.
Например, код 523 может представлять последовательность из трех байтов: 231 124 234. Всякий раз, когда алгоритм сжатия обнаруживает последовательность во входном файле, в кодируемый файл ставится код 523. При распаковке код 523 преобразуется с помощью таблицы в исходную последовательность из трех байтов. Чем длиннее последовательность, назначаемая единичному коду и чем чаще она повторяется, тем больше коэффициент сжатия.
Существуют два основных препятствия при использовании этого метода сжатия: 1) как определить, какие последовательности должны указываться в кодовой таблице и 2) как обеспечить программу распаковки той же таблицей, которую использует программа сжатия. Алгоритм LZW позволяет решить эти задачи.
Когда программа LZW начинает кодировать файл, таблица содержит лишь первые 256 элементов — остальная ее часть пуста. Это значит, что первые коды, поступающие в сжимаемый файл, представляют собой единичные байты исходного файла, преобразуемые в 12-бит группы. По мере продолжения кодирования LZW-алгоритм определяет повторяющиеся последовательности данных и добавляет их в кодовую таблицу. Сжатие начинается, когда последовательность обнаруживается вторично. Суть метода в том, что последовательность из входящего файла не добавляется в кодовую таблицу, если она уже была помещена в сжатый файл как отдельный символ (коды 0—255). Это важное условие, поскольку оно позволяет программе распаковки восстановить кодовую таблицу непосредственно из сжатых данных, не нуждаясь в ее отдельной передаче.
Сжатие начинается, когда последовательность обнаруживается вторично. Суть метода в том, что последовательность из входящего файла не добавляется в кодовую таблицу, если она уже была помещена в сжатый файл как отдельный символ (коды 0—255). Это важное условие, поскольку оно позволяет программе распаковки восстановить кодовую таблицу непосредственно из сжатых данных, не нуждаясь в ее отдельной передаче.
JPEG
Из множества алгоритмов сжатия с потерями кодирование с преобразованием оказалось наиболее востребованным. Наилучший пример такого метода — популярный стандарт JPEG (Joint Photographers Experts Group — Объединенная группа экспертов по машинной обработке фотографических изображений). Рассмотрим на примере JPEG работу алгоритма сжатия с потерями.
Мы уже обсудили простейший метод сжатия с потерями CS&Q, в котором уменьшается количество битов на выборку или полностью отбрасываются некоторые выборки. Оба этих приема позволяют достичь желаемого результата — файл становится меньше за счет ухудшения качества сигнала. Понятно, что эти простые методы работают не самым лучшим образом.
Понятно, что эти простые методы работают не самым лучшим образом.
Сжатие с преобразованием основано на простом условии: в трансформированном сигнале (например, с помощью преобразования Фурье) полученные значения данных не несут прежней информационной нагрузки. В частности, низкочастотные компоненты сигнала начинают играть более важную роль, чем высокочастотные компоненты. Удаление 50% битов из высокочастотных компонентов может привести, например, к удалению лишь 5% закодированной информации.
Из рисунка 7 видно, что JPEG-сжатие начинается путем разбиения изображения на группы размером 8×8 пикселов. Полный алгоритм JPEG работате с широким рядом битов на пиксел, включая информацию о цвете. В этом примере каждый пиксел является единичным байтом, градацией серого в диапазоне 0—255. Эти группы 8×8 пикселов обрабатываются при сжатии независимо друг от друга. Это значит, что каждая группа сначала представляется 64 байтами. Вслед за преобразованием и удалением данных каждая группа представляется, например, 2—20 байтами. При распаковке сжатого файла требуется такое же количество байтов для аппроксимации исходной группы 8×8. Эти аппроксимированные группы затем объединяются, воссоздавая несжатое изображение. Почему используются группы размерами 8×8, а не 16×16? Такое группирование было основано исходя из максимального возможного размера, с которым работали микросхемы на момент разработки стандарта.
При распаковке сжатого файла требуется такое же количество байтов для аппроксимации исходной группы 8×8. Эти аппроксимированные группы затем объединяются, воссоздавая несжатое изображение. Почему используются группы размерами 8×8, а не 16×16? Такое группирование было основано исходя из максимального возможного размера, с которым работали микросхемы на момент разработки стандарта.
Рис. 7. Пример применения метода сжатия JPEG. Три группы 8?8, показанные в увеличенном виде, представляют значения отдельных пикселов |
Для реализации методов сжатия было исследовано множество различных преобразований. Например, преобразование Karhunen-Loeve обеспечивает наиболее высокий коэффициент сжатия, но оно трудно осуществляется. Метод преобразования Фурье реализуется гораздо проще, но он не обеспечивает достаточно хорошего сжатия. В конце концов, выбор был сделан в пользу разновидности метода Фурье — дискретного косинусного преобразования (Discrete Cosine Transform — DCT).
На примере работы алгоритма JPEG видно, как несколько схем сжатия объединяются, обеспечивая большую эффективность. Вся процедура сжатия JPEG состоит из следующих этапов:
– изображение разбивается на группы 8×8;
– каждая группа преобразуется с помощью преобразования DCT;
– каждый спектральный элемент 8×8 сжимается путем сокращения числа битов и удаления некоторых компонентов с помощью таблицы квантования;
– видоизмененный спектр преобразуется из массива 8×8 в линейную последовательность, все высокочастотные компоненты которой помещаются в ее конец;
– серии нулей сжимаются с помощью метода RLE;
– последовательность кодируется либо методом Хаффмана, либо арифметическим методом для получения сжатого файла.
MPEG
MPEG (Moving Pictures Experts Group — Экспертная группа по кинематографии) — стандарт сжатия цифровых видеоданных. Этот алгоритм обеспечивает также сжатие звуковой дорожки к видеофильму. MPEG представляет собой еще более сложный, чем JPEG, стандарт с огромным потенциалом. Можно сказать, это ключевая технология XXI века.
Можно сказать, это ключевая технология XXI века.
У MPEG имеется несколько очень важных особенностей. Так например, он позволяет воспроизводить видеофильм в прямом и обратном направлениях, в режиме нормальной и повышенной скорости. К кодированной информации имеется прямой доступ, т.е. каждый отдельный кадр последовательности отображается как неподвижное изображение. Таким образом, фильм редактируется — можно кодировать его короткие фрагменты, не используя всю последовательность в качестве опорной. MPEG также устойчив к ошибкам, что позволяет избегать цифровых ошибок, приводящих к нежелательному прерыванию воспроизведения.
Используемый в этом стандарте метод можно классифицировать по двум типам сжатия: внутрикадровое и межкадровое. При сжатии по первому типу отдельные кадры, составляющие видеопоследовательность, кодируются так, как если бы они были неподвижными изображениями. Такое сжатие выполняется с помощью JPEG-стандарта с несколькими вариациями. В терминологии MPEG кадр, закодированный таким образом, называется внутрикодированным, или I-picture.
В терминологии MPEG кадр, закодированный таким образом, называется внутрикодированным, или I-picture.
Наибольшая часть пикселов в видеопоследовательности изменяется незначительно от кадра к кадру. Если камера не движется, наибольшая часть изображения состоит из фона, который не меняется на протяжении некоторого количества кадров. MPEG использует это обстоятельство, сжимая избыточную информацию между кадрами с помощью дельта-кодирования. После сжатия одного из кадров в виде I-picture последующие кадры кодируются как изображения с предсказанием, или P-pictures, т.е. кодируются только изменившиеся пикселы, т.к. кадры I-picture включены в P-picture.
Эти две схемы сжатия составляют основу MPEG, тогда как практическая реализация данного метода намного сложнее описанной. Например, кадры P-picture могут использовать изображение I-picture как опорное, которое претерпело изменение при перемещении объектов в последовательности изображений. Существуют также двунаправленные предиктивно-кодированные изображения, или B-pictures. Эти видеокадры формируются способом предсказания «вперед» и «назад» на основе I-picture. При этом обрабатываются участки изображения, которые постепенно меняются на протяжении множества кадров. Отдельные кадры также хранятся без соблюдения последовательности в сжатых данных, чтобы облегчить упорядочение изображений I-, P- и B-pictures. Наличие цвета и звука еще больше усложняет реализацию этого алгоритма.
Эти видеокадры формируются способом предсказания «вперед» и «назад» на основе I-picture. При этом обрабатываются участки изображения, которые постепенно меняются на протяжении множества кадров. Отдельные кадры также хранятся без соблюдения последовательности в сжатых данных, чтобы облегчить упорядочение изображений I-, P- и B-pictures. Наличие цвета и звука еще больше усложняет реализацию этого алгоритма.
Наибольшее искажение при использовании формата MPEG наблюдается при быстром изменении больших частей изображения. Для поддержания воспроизведения с быстро меняющимися сценами на должном уровне требуется значительный объем информации. Если скорость передачи данных ограничена, зритель в этом случае видит ступенчатообразные искажения при смене сцен. Эти искажения сводятся к минимуму в сетях с одновременной передачей данных по нескольким видеоканалам, например в сети кабельного телевидения. Внезапное увеличение объема данных, требуемое для поддержки быстро меняющейся сцены в видеоканале, компенсируется относительно статическими изображениями, передаваемыми по другим каналам.
Литература
1. Steven W. Smith, Data compression tutorial Part 1, Part 2, and Part 3.
Сжатие данных в примерах
Теория и стратегия представления данных
Девид Мертц (David Mertz)
Опубликовано 19.04.2012
Сжатие данных широко используется в самых разнообразных контекстах программирования. Все популярные операционные системы и языки программирования имеют многочисленные инструментальные средства и библиотеки для работы с различными методами сжатия данных.
Правильный выбор инструментальных средств и библиотек сжатия для конкретного приложения зависит от характеристик данных и назначения самого приложения: потоковой передачи данных или работы с файлами; ожидаемых шаблонов и закономерностей в данных; относительной важности использования ресурсов ЦП и памяти, потребностей в каналах передачи и требований к хранению и других факторов.
Что понимается под сжатием данных? Если говорить кратко, то сжатие устраняет из данных избыточность; в терминах же теории информации сжатие увеличивает энтропию сжатого текста. Однако оба этих утверждения по существу по существу верны в силу определения самих понятий. Избыточность может быть выражена в самых разных формах. Одним типом является последовательности повторяющихся битов (11111111). Вторым – последовательности повторяющихся байтов (XXXXXXXX). Однако чаще избыточность проявляется в более крупном масштабе и выражается либо закономерностями в наборе данных, взятом как единое целое, либо последовательностями различной длины, имеющими общие признаки. По существу, цель сжатия данных заключается в поиске алгоритмических преобразований представлений данных, которые позволят получить более компактные представления «типовых» наборов данных. Это описание может показаться несколько туманным, но мы постараемся раскрыть его суть на практических примерах.
По существу, цель сжатия данных заключается в поиске алгоритмических преобразований представлений данных, которые позволят получить более компактные представления «типовых» наборов данных. Это описание может показаться несколько туманным, но мы постараемся раскрыть его суть на практических примерах.
Сжатие без потерь и с потерями
Фактически существуют два в корне различающихся подхода к сжатию данных: сжатие с потерями и без потерь. Эта статья, в основном, посвящена методам сжатия без потерь, но для начала полезно изучить различия. Сжатие без потерь предусматривает преобразование представления набора данных таким образом, чтобы затем можно было в точности воспроизвести первоначальный набор данных путем обратного преобразования (распаковки). Сжатие с потерями – это представление, которое позволяет воспроизводить нечто «очень похожее» на первоначальный набор данных. Преимущество использования методов сжатия с потерями заключается в том, что они зачастую позволяют получать намного более компактные представления данных по сравнению с методами сжатия без потерь. Чаще всего методы сжатия с потерями применяются для обработки изображений, звуковых файлов и видео. Сжатие с потерями в этих областях может оказаться уместным благодаря тому, что человек воспринимает битовую комбинацию цифрового изображения/звука не с «побитовой» точностью, а скорее оценивает музыку или изображение в целом.
Чаще всего методы сжатия с потерями применяются для обработки изображений, звуковых файлов и видео. Сжатие с потерями в этих областях может оказаться уместным благодаря тому, что человек воспринимает битовую комбинацию цифрового изображения/звука не с «побитовой» точностью, а скорее оценивает музыку или изображение в целом.
С точки зрения «обычных» данных сжатие с потерями – неудачный вариант. Нам не нужна программа, которая делает «примерно» то, а не точно то, что было запрошено в действительности. То же касается и баз данных, которые должны хранить именно те данные, которые были в них загружены. По крайней мере, это не подойдет для решения большинства задач (и мне известно очень мало практических примеров использования сжатия с потерями за пределами тех данных, которые сами по себе описывают чувственное восприятие реального мира (например, изображений и звуков)).
Пример набора данных
В данной статье будет использоваться специально подготовленное гипотетическое представление данных. Приведем простой для понимания пример. В городе Гринфилд (штат Массачусетс, США) используются префиксы телефонных номеров
Приведем простой для понимания пример. В городе Гринфилд (штат Массачусетс, США) используются префиксы телефонных номеров 772-, 773- и 774-. (К сведению читателей за пределами США: в США местные телефонные номера являются семизначными и традиционно представляются в виде ###-####; префиксы назначаются в соответствии с географическим местоположением). Также предположим, что из всех трех префиксов чаще всего используется первый. Частями суффикса могут быть любые другие цифры с приблизительно равной вероятностью. Набор интересующих нас данных находится в «списке всех телефонных номеров, которые в настоящее время находятся в активном пользовании». Можно попробовать подобрать причину, почему это могло бы быть интересным с точки зрения программирования, но в данном случае это не важно.
Изначально интересующий нас набор данных имеет стандартное представление: многоколоночный отчет (возможно, сгенерированный в качестве результата выполнения какого-либо запроса или процесса компиляции). Первые несколько строк этого отчета могли бы выглядеть следующим образом:
Первые несколько строк этого отчета могли бы выглядеть следующим образом:
Таблица 1. Многоколоночный отчет
============================================================= 772-7628 772-8601 772-0113 773-3429 774-9833 773-4319 774-3920 772-0893 772-9934 773-8923 773-1134 772-4930 772-9390 774-9992 772-2314 [...]
Сжатие пустых мест
Сжатие пустых мест может быть охарактеризовано в более общем смысле как «удаление того, что нас не интересует». Даже несмотря на то, что этот метод с технической точки зрения представляет собой метод сжатия с потерями, он все равно полезен для многих типов представлений данных, с которыми мы сталкиваемся в реальном мире. Например, даже несмотря на то, что HTML намного удобнее читать в текстовом редакторе при добавлении отступов и междустрочных интервалов, ни одно из этих «пустых мест» никак не влияет на визуализацию HTML-документа в Web-браузере. Если вам точно известно, что конкретный документ HTML предназначается исключительно для Web-браузера (или для какого-либо робота/поискового агента), то, возможно, будет неплохо убрать все пустые места, чтобы документ передавался быстрее и занимал меньше места в хранилище. Все то, что мы удаляем при сжатии пустых мест, в действительности не несет никакой функциональной нагрузки.
Все то, что мы удаляем при сжатии пустых мест, в действительности не несет никакой функциональной нагрузки.
В случае с представленным примером из описанного отчета можно удалить лишь небольшую часть информации. Строка символов «=» по верхнему краю отчета не несет никакого функционального наполнения; то же самое касается символов «-» в номерах и пробелов между номерами. Все это полезно для человека, читающего исходный отчет, но не имеет никакого значения, если мы рассматриваем эти символы в качестве «данных». То, что мы удаляем, – это не совсем «пустое место» в традиционном смысле, но является им по сути.
Сжатие пустых мест крайне «дешево» с точки зрения реализации. Вопрос состоит лишь в считывании потока данных и исключении из выходного потока нескольких конкретных значений. Во многих случаях этап «распаковки» вообще не предусматривается. Однако даже если бы мы захотели воссоздать что-то близкое к оригиналу потока данных, это потребовало бы лишь небольшого объема ресурсов ЦП или памяти. Восстановленные данные не обязательно будут совпадать с исходными данными; это зависит от того, какие правила и ограничения содержались в оригинале. Страница HTML, напечатанная человеком в текстовом редакторе, вероятно, будет содержать пробелы, расставленные согласно определенным правилам. Это же относится и к автоматизированным инструментальным средствам, которые часто создают «обоснованные» отступы и интервалы в коде HTML. В случае с жестким форматом отчета, представленным в нашем примере, не существует никаких причин, по которым первоначальное представление не могло бы быть воссоздано каким-либо «форматирующим распаковщиком».
Восстановленные данные не обязательно будут совпадать с исходными данными; это зависит от того, какие правила и ограничения содержались в оригинале. Страница HTML, напечатанная человеком в текстовом редакторе, вероятно, будет содержать пробелы, расставленные согласно определенным правилам. Это же относится и к автоматизированным инструментальным средствам, которые часто создают «обоснованные» отступы и интервалы в коде HTML. В случае с жестким форматом отчета, представленным в нашем примере, не существует никаких причин, по которым первоначальное представление не могло бы быть воссоздано каким-либо «форматирующим распаковщиком».
Групповое кодирование
Групповое кодирование (RLE) является простейшим из широко используемых методов сжатия без потерь. Подобно сжатию пустых мест, оно не требует особых затрат, особенно для декодирования. Идея, стоящая за данным методом, заключается в том, что многие представления данных состоят большей частью из строк повторяющихся байтов. Наш образец отчета является одним из таких представлений данных. Он начинается со строки повторяющихся символов «=» и имеет разбросанные по отчету строки, состоящие только из пробелов. Вместо того чтобы представлять каждый символ с помощью его собственного байта, метод RLE предусматривает (иногда или всегда) указание количества повторений, за которым следует символ, который необходимо воспроизвести указанное число раз.
Он начинается со строки повторяющихся символов «=» и имеет разбросанные по отчету строки, состоящие только из пробелов. Вместо того чтобы представлять каждый символ с помощью его собственного байта, метод RLE предусматривает (иногда или всегда) указание количества повторений, за которым следует символ, который необходимо воспроизвести указанное число раз.
Если в обрабатываемом формате данных преобладают повторяющиеся байты, то может быть уместным и эффективным использование алгоритма, в котором один или несколько байтов указывают количество повторений, а затем следует повторяемый символ. Однако если имеются строки символов единичной длины, для их кодирования потребуются два (или более) байта. Другими словами, для одного символа ASCII «X» входного потока мог бы потребоваться выходной битовый поток 00000001 01011000. С другой стороны, для кодирования ста следующих друг за другом символов «X» использовалось бы то же самое количество битов: 01100100 01011000, что весьма эффективно.
В различных вариантах RLE часто применяется избирательное использование байтов для указания числа повторений, в то время как остальные байты просто представляют сами себя. Для этого должно быть зарезервировано как минимум одно однобайтовое значение, которое в случае необходимости может удаляться из выходных данных. Например, в нашем образце отчета по телефонным номерам известно, что вся информация во входном потоке состоит из простых символов ASCII. В частности, у всех таких символов первый бит ASCII-значения равен 0. Мы могли бы использовать этот первый бит ASCII для указания на то, что байт указывает число повторений, а не обычный символ. Следующие семь битов байта итератора могли бы использоваться для указания числа повторений, а в следующем байте мог бы содержаться повторяющийся символ. Так, например, мы могли бы представить строку «YXXXXXXXX» следующим образом:
"Y" Iter(8) "X" 01001111 10001000 01011000
Этот пример не объясняет, как отбрасывать значения байта итератора и не предусматривает возможности использования более 127 повторений одного символа. Однако различные вариации RLE при необходимости решают и эти задачи.
Однако различные вариации RLE при необходимости решают и эти задачи.
Кодирование по методу Хаффмана
Кодирование по методу Хаффмана рассматривает таблицу символов как целый набор данных. Сжатие достигается путем нахождения «весовых коэффициентов» каждого символа в наборе данных. Некоторые символы используются чаще других, поэтому кодирование по методу Хаффмана предполагает, что частые символы должны кодироваться меньшим количеством бит, чем более редкие символы. Существуют различные варианты кодирования по методу Хаффмана, но исходный (и чаще всего применяемый) вариант включает поиск самого распространенного символа и кодирование его одним битом, например, 1. И если в закодированной последовательности встречается 0, это значит, что на этом месте находится другой символ, закодированный большим количеством бит.
Представим, что мы применили кодирование по методу Хаффмана для кодирования нашего примера (предположим, что мы уже подвергли отчет сжатию пустых мест). Мы могли бы получить следующий результат:
Таблица 2. Результаты кодирования по методу Хаффмана
Результаты кодирования по методу Хаффмана
Encoding Symbol 1 7 010 2 011 3 00000 4 00001 5 00010 6 00011 8 00100 9 00101 0 00111 1
Исходный набор символов (состоящий из чисел) может быть легко закодирован (без сжатия) в виде 4-х битных последовательностей (полубайтов). Приведенное кодирование по методу Хаффмана будет использовать до 5 битов для символов в наихудшем случае, что очевидно хуже кодирования с помощью полубайтов. Однако в лучшем случае потребуется всего 1 бит; при этом известно, что именно лучший случай будет использоваться чаще всего (так как именно этот символ чаще всего встречается в данных). Таким образом, мы могли бы закодировать конкретный телефонный номер следующим образом:
772 7628 --> 1 1 010 1 00010 010 00011
При кодировании с помощью полубайтов представление телефонного номера заняло бы 28 бит, в нашем же случае кодирование занимает 19 бит. Пробелы добавлены в пример только для лучшего восприятия; их присутствие в кодированных символах не требуется, так как по таблице кодов всегда можно определить, достигнут конец закодированного символа или нет (правда, при этом все равно необходимо отслеживать текущую позицию в данных).
Пробелы добавлены в пример только для лучшего восприятия; их присутствие в кодированных символах не требуется, так как по таблице кодов всегда можно определить, достигнут конец закодированного символа или нет (правда, при этом все равно необходимо отслеживать текущую позицию в данных).
Кодирование по методу Хаффмана по-прежнему является очень «дешевым» для декодирования с точки зрения процессорного времени. Однако оно требует поиска в таблице кодов, поэтому не может быть столь же «дешевым», как RLE. Кодирование по методу Хаффмана является довольно затратным, так как требует полного сканирования данных и построения таблицы частот символов. В некоторых случаях при использовании кодирования по методу Хаффмана уместным является «короткий путь». Стандартное кодирование по методу Хаффмана применяется к конкретному кодируемому набору данных, при этом в выходных данных вначале следует таблица символов. Однако если передается не одиночный набор данных, а целый формат с одинаковыми закономерностями встречаемости символов, то можно использовать глобальную таблицу Хаффмана. При наличии такой таблицы мы можем жестко запрограммировать поиск в своих исполняемых файлах, что значительно «удешевит» сжатие и распаковку (за исключением начальной глобальной дискретизации и жесткого кодирования). Например, если мы знаем, что наш набор данных будет представлять собой прозу на английском языке, то частоты появления букв хорошо известны и постоянны для различных наборов данных.
При наличии такой таблицы мы можем жестко запрограммировать поиск в своих исполняемых файлах, что значительно «удешевит» сжатие и распаковку (за исключением начальной глобальной дискретизации и жесткого кодирования). Например, если мы знаем, что наш набор данных будет представлять собой прозу на английском языке, то частоты появления букв хорошо известны и постоянны для различных наборов данных.
Сжатие по алгоритму Лемпеля-Зива
Вероятно, самым значимым методом сжатия без потерь является алгоритм Лемпеля-Зива. В этой статье речь пойдет о варианте LZ78, но LZ77 и другие варианты работают схожим образом. Идея, заложенная в алгоритме LZ78, заключается в кодировании потоковой последовательности байтов с использованием некоторой динамической таблицы. В начале сжатия битового потока таблица LZ заполняется фактическим набором символов, наряду с несколькими пустыми слотами. В алгоритме применяются таблицы разных размеров, но в данном примере с телефонными номерами (со сжатием пустых мест) используется таблица из 32 элементов (этого достаточно для данного примера, но может оказаться мало для других типов данных). Вначале мы заполняем первые десять слотов символами используемого алфавита (цифрами). По мере поступления новых байтов сначала выводится значение из таблицы, соответствующее самой длинной подходящей последовательности, а затем в следующий доступный слот записывается последовательность длиной N+1. В наихудшем случае мы используем 5 битов вместо 4 для отдельного символа, однако в большинстве случаев мы сможем обойтись 5 битами на несколько символов. Рассмотрим пример работы этого алгоритма (слот таблицы указан в квадратных скобках):
Вначале мы заполняем первые десять слотов символами используемого алфавита (цифрами). По мере поступления новых байтов сначала выводится значение из таблицы, соответствующее самой длинной подходящей последовательности, а затем в следующий доступный слот записывается последовательность длиной N+1. В наихудшем случае мы используем 5 битов вместо 4 для отдельного символа, однако в большинстве случаев мы сможем обойтись 5 битами на несколько символов. Рассмотрим пример работы этого алгоритма (слот таблицы указан в квадратных скобках):
7 --> Поиск: 7 найдено --> добавлять нечего --> продолжить поиск 7 --> Поиск: 77 не найдено --> добавить '77' to [11] --> вывести [7]=00111 2 --> Поиск: 72 не найдено --> добавить '72' to [12] --> вывести [7]=00111 7 --> Поиск: 27 не найдено --> добавить '27' to [13] --> вывести [2]=00010 6 --> Поиск: 76 не найдено --> добавить '76' to [14] --> вывести [7]=00111 2 --> Поиск: 62 не найдено --> добавить '62' to [15] --> вывести [6]=00110 8 --> Поиск: 28 не найдено --> добавить '28' to [16] --> вывести [2]=00010
До сих пор мы не извлекли из этого никакой пользы, но давайте перейдем к следующему телефонному номеру:
7 --> Поиск: 87 не найдено --> добавить '87 to [17] --> вывести [8]=00100 7 --> Поиск: 77 найдено --> добавлять нечего --> продолжить поиск 2 --> Поиск: 772 не найдено --> добавить '772' to [18] --> вывести [11]=01011 8 --> Поиск: 28 найдено --> добавлять нечего --> продолжить поиск 6 --> Поиск: 286 не найдено --> добавить '286' to [19] --> вывести [16]=10000 ....
Приведенных операций должно быть достаточно для демонстрации работы модели. Хотя никакого заметного сжатия пока не достигнуто, уже видно, что мы повторно использовали слоты 11 и 16, закодировав по два символа одним выходным символом. Кроме того, мы уже накопили крайне полезную последовательность байтов 772 в слоте 18, которая впоследствии неоднократно будет встречаться в потоке.
Алгоритм LZ78 заполняет одну таблицу символов полезными (предположительно) записями, затем записывает эту таблицу, очищает ее и начинает новую. В такой ситуации таблица из 32 символов может оказаться недостаточной, так как будет очищена прежде, чем нам удастся неоднократно воспользоваться такими последовательностями, как 772 и ей подобные. Однако с помощью небольшой таблицы проще проиллюстрировать работу алгоритма.
В типичных наборах данных варианты метода Лемпеля-Зива достигают значительно более высоких коэффициентов сжатия, чем методы Хаффмана и RLE. С другой стороны, варианты метода Лемпеля-Зива тратят значительные ресурсы на итерации, а их таблицы могут занимать много места в памяти. Большинство существующих инструментальных средств и библиотек сжатия используют комбинацию методов Лемпеля-Зива и Хаффмана.
Правильная постановка задачи
Выбрав правильный алгоритм, можно получить значительный выигрыш даже по сравнению с более оптимизированными, но неподходящими методами. Точно так же правильный выбор представления данных зачастую оказывается важнее выбора методов сжатия (которые всегда являются своего рода последующей оптимизацией требуемых функций). Простой пример набора данных, приводимый в этой статье, служит отличной иллюстрацией ситуации, когда переосмысление проблемы будет более удачным решением, чем использование любого из приведенных методов сжатия.
Необходимо еще раз взглянуть на проблему, которую представляют данные. Так как это не общий набор данных и для него существуют четкие предварительные требования, то проблему можно переформулировать. Известно, что существует максимум 30000 телефонных номеров (от 7720000 до 7749999), некоторые из которых являются активными, а некоторые – нет. Перед нами не стоит задача вывести полное представление всех активных номеров. Нам просто требуется указать с помощью логического значения, активен данный номер или нет. Размышляя о проблеме подобным образом, мы можем просто выделить 30000 битов в памяти и в системе хранения и использовать каждый бит для индикации активности («да» или «нет») соответствующего телефонного номера. Порядок битов в битовом массиве может соответствовать телефонным номерам, отсортированным по возрастанию (от меньшего к большему).
Подобное решение на основе битового массива идеально со всех точек зрения. Оно требует ровно 3750 байт для представления набора данных; различные методы сжатия будут использовать меняющийся объем в зависимости от количества телефонных номеров в наборе и эффективности сжатия. Однако если 10000 из 30000 возможных телефонных номеров являются активными и если даже самому эффективному методу сжатия требуется несколько байтов на один телефонный номер, то битовый массив однозначно выигрывает. С точки зрения потребностей в ресурсах ЦП битовый массив не только превосходит любой из рассмотренных методов сжатия, но и оказывается лучше, чем обычный метод представления телефонных номеров в виде строк (без сжатия). Проход по битовому массиву и увеличение счетчика текущего телефонного номера могут эффективно выполняться даже во встроенном кэше современных процессоров.
Из этого простого примера можно понять, что далеко не каждая проблема имеет такое идеальное решение, как рассмотренная выше. Многие проблемы действительно требуют использования значительного объема ресурсов памяти, пропускной способности, хранилища и ЦП; и в большинстве подобных случаев методы сжатия могут облегчить или снизить эти требования. Но более важный вывод состоит в том, что перед применением методов сжатия стоит еще раз удостовериться, что для представления данных выбрана правильная концепция.
Посвящается памяти Клода Шеннона (Claude Shannon).
Ресурсы для скачивания
Похожие темы
Методы сжатия информации — это… Что такое Методы сжатия информации?
- Методы сжатия информации
Сжатие данных — процедура перекодирования данных, производимая с целью уменьшения их объёма. Применяется для более рационального использования устройств хранения и передачи данных.
Сжатие бывает без потерь (когда возможно восстановление исходных данных без искажений) или с потерями (восстановление возможно с искажениями, несущественными с точки зрения дальнейшего использования восстановленных данных). Сжатие без потерь обычно используется при обработке компьютерных программ и данных, реже — для сокращения объёма звуковой, фото- и видеоинформации. Сжатие с потерями применяется для сокращения объёма звуковой, фото- и видеоинформации, оно значительно эффективнее сжатия без потерь.
Сжатие основано на устранении избыточности информации, содержащейся в исходных данных. Примером избыточности является повторение в тексте фрагментов (например, слов естественного или машинного языка). Подобная избыточность обычно устраняется заменой повторяющейся последовательности более коротким значением (кодом). Другой вид избыточности связан с тем, что некоторые значения в сжимаемых данных встречаются чаще других, при этом возможно заменять часто встречающиеся данные более короткими кодами, а редкие — более длинными (вероятностное сжатие). Сжатие данных, не обладающих свойством избыточности (например, случайный сигнал или шум), невозможно без потерь. Также, обычно невозможно сжатие зашифрованной информации.
Алгоритмы сжатия текстов/файлов неизвестного формата
Имеется 2 основных подхода к сжатию файлов неизвестного формата.
- На каждом шаге алгоритма сжатия либо следующий символ помещается как есть (со специальным флагом помечающим, что он не сжат), либо указываются границы слова из предыдущего куска, которое совпадает со следующими символами файла. Разархивирование сжатых таким образом файлов выполняется очень быстро, поэтому эти алгоритмы используются для создания самораспаковывающихся программ.
- Для каждой последовательности в каждый момент времени собирается статистика её встречаемости в файле. На основе этой статистики вычисляется вероятность значений для очередного символа. После этого можно применять ту или иную разновидность статистического кодирования, например, арифметическое кодирование или кодирование Хаффмана для замены часто встречающихся последовательностей на более короткие, а редко встречающихся — на более длинные.
Библиография
- Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео. — Диалог-МИФИ, 2002. — С. 384. — ISBN 5-86404-170-X 3000 экз.
- Д. Сэломон. Сжатие данных, изображения и звука. — М.: Техносфера, 2004. — С. 368. — ISBN 5-94836-027-X 3000 экз.
См. также
Ссылки
Wikimedia Foundation.
2010.
- Методы развития творческого воображения
- Методы сортировки
Смотреть что такое «Методы сжатия информации» в других словарях:
МЕТОДЫ КЛАССИФИКАЦИИ — совокупность методов статистич. многомерного анализа. В зависимости от того, в какой области научн. знаний М.к. возникли и получили свое развитие, они наз. методами многомерной классификации, таксономии, кластерного анализа, группировки,… … Российская социологическая энциклопедия
МЕТОДЫ КЛАССИФИКАЦИИ — – составная часть методов многомерного анализа. М. к. заключаются в разбиении совокупности объектов на отдельные классы так, что объекты, отнесенные к одному классу, считаются похожими, однотипными, близкими, а отнесенные к разным классам –… … Энциклопедический словарь по психологии и педагогике
ИНФОРМАЦИИ ТЕОРИЯ — раздел математики, исследующий процессы хранения, преобразования и передачи информации. В основе его лежит определенный способ измерения количества информации. Возникшая из задач теории связи, теория информации иногда рассматривается как… … Энциклопедия Кольера
Сжатие информации — Сжатие информации, компрессия, Шаблон:Англ. data compression алгоритмическое преобразование данных (кодирование), при котором за счет уменьшения их избыточности уменьшается их обьём. Содержание 1 Принципы сжатия информации … Википедия
Избыточность информации — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия
Алгоритм сжатия PPM — У этого термина существуют и другие значения, см. Ppm. PPM (англ. Prediction by Partial Matching предсказание по частичному совпадению) адаптивный статистический алгоритм сжатия данных без потерь, основанный на контекстном… … Википедия
Нат (единица измерения информации) — Нат больше бита, но немного меньше трита. Жёлтая кривая график логарифма. Нат одна из единиц измерения информации. Определяется через натуральный логарифм, в отличие от других единиц, где основание логарифма является целым числом. Применяется в … Википедия
Нат (Единица измерения информации) — Нат больше бита, но немного меньше трита. Жёлтая кривая график логарифма. Нат одна из единиц измерения информации. Определяется через натуральный логарифм, в отличие от других единиц, где основание логарифма является целым числом. Применяется в … Википедия
Нат (теория информации) — У этого термина существуют и другие значения, см. Нат. Единицы измерения информации бит, нат, трит и бан (децит) Нат одна из единиц измерения информации. Определяется через натуральный … Википедия
Кодирование звуковой информации — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. В основе кодирования звука с использованием ПК лежит процесс преобразования колебаний воздуха в колебания электрическог … Википедия
Книги
- Методы творчества в интеграционной механике для преодоления Информационного цунами, Д. Ф. Полищук, А. Д. Полищук. Интеграционная механика представляет новое направление в интеграции знания как единство математики, физики и прикладной философии, предназначенное для решения взаимосвязанных нелинейных задач… Подробнее Купить за 852 грн (только Украина)
- По океану дискретной математики. От перечислительной комбинаторики до современной криптографии. Основные структуры. Методы перечисления. Булевы функции. Том 1, Зуев Ю.А.. Содержание настоящей книги охватывает вузовский курс дискретной математики, включая перечислительную комбинаторику, булевы функции, графы, алгоритмы, помехоустойчивое кодирование и… Подробнее Купить за 796 руб
- Методы творчества в интеграционной механике для преодоления «Информационного цунами», Полищук Д.Ф.. Интеграционная механика представляет новое направление в интеграции знания как единство математики, физики и прикладной философии, предназначенное для решения взаимосвязанных нелинейных задач… Подробнее Купить за 659 руб
Другие книги по запросу «Методы сжатия информации» >>
Сжатие без потерь — Lossless compression
Подход к сжатию данных, позволяющий идеально восстановить исходные данные
Сжатие без потерь — это класс алгоритмов сжатия данных , который позволяет полностью восстановить исходные данные из сжатых данных. Напротив, сжатие с потерями позволяет восстановить только аппроксимацию исходных данных, хотя обычно со значительно улучшенными степенями сжатия (и, следовательно, уменьшенными размерами носителя).
Благодаря принципу работы с ячейками ни один алгоритм сжатия без потерь не может эффективно сжать все возможные данные. По этой причине существует множество различных алгоритмов, которые разработаны либо с учетом конкретного типа входных данных, либо с конкретными предположениями о том, какие виды избыточности могут содержать несжатые данные.
Сжатие данных без потерь используется во многих приложениях. Например, он используется в формате файла ZIP и в инструменте GNU gzip . Он также часто используется в качестве компонента в технологиях сжатия данных с потерями (например, совместная предварительная обработка стерео среднего и бокового каналов без потерь с помощью кодеров MP3 и других кодеров аудио с потерями).
Сжатие без потерь используется в тех случаях, когда важно, чтобы исходные и распакованные данные были идентичны, или когда отклонения от исходных данных были бы нежелательными. Типичными примерами являются исполняемые программы, текстовые документы и исходный код. Некоторые форматы файлов изображений, такие как PNG или GIF , используют только сжатие без потерь, в то время как другие, такие как TIFF и MNG, могут использовать методы без потерь или с потерями. Аудиоформаты без потерь чаще всего используются для архивирования или производства, тогда как аудиофайлы меньшего размера с потерями обычно используются на портативных плеерах и в других случаях, когда пространство для хранения ограничено или точное воспроизведение звука не требуется.
Методы сжатия без потерь
Большинство программ сжатия без потерь выполняют две операции последовательно: на первом этапе создается статистическая модель для входных данных, а на втором этапе эта модель используется для сопоставления входных данных с последовательностями битов таким образом, чтобы «вероятные» (например, часто встречающиеся) данные даст более короткий результат, чем «невероятные» данные.
Основными алгоритмами кодирования, используемыми для создания битовых последовательностей, являются кодирование Хаффмана (также используемое DEFLATE ) и арифметическое кодирование . Арифметическое кодирование обеспечивает степень сжатия, близкую к наилучшей из возможных для конкретной статистической модели, которая задается информационной энтропией , тогда как сжатие Хаффмана проще и быстрее, но дает плохие результаты для моделей, которые имеют дело с вероятностями символа, близкими к 1.
Существует два основных способа построения статистических моделей: в статической модели данные анализируются и строится модель, затем эта модель сохраняется со сжатыми данными. Этот подход прост и модулен, но имеет недостаток, заключающийся в том, что сама модель может быть дорогостоящей в хранении, а также в том, что он вынуждает использовать единую модель для всех сжимаемых данных и поэтому плохо работает с файлами, содержащими разнородные данные. Адаптивные модели динамически обновляют модель по мере сжатия данных. И кодер, и декодер начинаются с тривиальной модели, что приводит к плохому сжатию исходных данных, но по мере того, как они узнают больше о данных, производительность улучшается. В наиболее популярных типах сжатия, используемых на практике, сейчас используются адаптивные кодеры.
Методы сжатия без потерь можно разделить на категории в соответствии с типом данных, для сжатия которых они предназначены. Хотя, в принципе, любой алгоритм сжатия без потерь общего назначения ( универсальный означает, что они могут принимать любую строку битов) может использоваться для любого типа данных, многие из них не могут достичь значительного сжатия данных, которые не имеют формы, для которой они были созданы для сжатия. Многие методы сжатия без потерь, используемые для текста, также достаточно хорошо работают для индексированных изображений .
Мультимедиа
Эти методы используют преимущества определенных характеристик изображений, таких как обычное явление непрерывных двухмерных областей схожих тонов. Каждый пиксель, кроме первого, заменяется разницей его левого соседа. Это приводит к тому, что малые значения имеют гораздо большую вероятность, чем большие значения. Это часто также применяется к звуковым файлам и может сжимать файлы, содержащие в основном низкие частоты и небольшую громкость. Для изображений этот шаг можно повторить, взяв разницу в верхний пиксель, а затем в видео можно взять разницу в пикселе в следующем кадре.
Иерархическая версия этого метода берет соседние пары точек данных, сохраняет их разность и сумму, а на более высоком уровне с более низким разрешением продолжает вычисление сумм. Это называется дискретным вейвлет-преобразованием . JPEG2000 дополнительно использует точки данных из других пар и коэффициенты умножения, чтобы смешать их с разницей. Эти множители должны быть целыми числами, чтобы результат был целым при любых обстоятельствах. Значения увеличиваются, увеличивается размер файла, но, надеюсь, распределение значений более пиковое.
Адаптивное кодирование использует вероятности из предыдущего образца при кодировании звука, от левого и верхнего пикселя при кодировании изображения и дополнительно из предыдущего кадра при кодировании видео. В вейвлет-преобразовании вероятности также проходят через иерархию.
Исторические правовые вопросы
Многие из этих методов реализованы в открытых и проприетарных инструментах, особенно в LZW и его вариантах. Некоторые алгоритмы запатентованы в США и других странах, и их законное использование требует лицензирования держателем патента. Из-за патентов на определенные виды сжатия LZW и, в частности, практики лицензирования со стороны патентообладателя Unisys, которую многие разработчики сочли оскорбительной, некоторые сторонники открытого исходного кода рекомендовали людям избегать использования формата обмена графическими данными (GIF) для сжатия файлов неподвижных изображений в пользу Portable. сетевая графика (PNG), который сочетает в себе LZ77 основанном Deflate алгоритм с выбором фильтров предсказания предметно-ориентированным. Однако 20 июня 2003 г. истек срок действия патентов на LZW.
Многие из методов сжатия без потерь, используемых для текста, также достаточно хорошо работают для индексированных изображений , но есть другие методы, которые не работают для типичного текста, которые полезны для некоторых изображений (особенно простых растровых изображений), и другие методы, которые используют преимущества определенных характеристики изображений (такие как обычное явление смежных двухмерных областей схожих тонов и тот факт, что цветные изображения обычно имеют преобладание ограниченного диапазона цветов из тех, которые представляются в цветовом пространстве).
Как упоминалось ранее, сжатие звука без потерь — это несколько специализированная область. Алгоритмы сжатия звука без потерь могут использовать повторяющиеся шаблоны, показанные волнообразной природой данных — по сути, с использованием авторегрессионных моделей для прогнозирования «следующего» значения и кодирования (надеюсь, небольшой) разницы между ожидаемым значением и фактическими данными. Если разница между предсказанными и фактическими данными (называемая ошибкой ) имеет тенденцию быть небольшой, то определенные значения разницы (например, 0, +1, -1 и т. Д. В выборочных значениях) становятся очень частыми, что можно использовать путем их кодирования. в нескольких выходных битах.
Иногда полезно сжать только различия между двумя версиями файла (или, при сжатии видео , последовательных изображений в последовательности). Это называется дельта-кодированием (от греческой буквы Δ , которая в математике обозначает различие), но этот термин обычно используется только в том случае, если обе версии имеют смысл вне сжатия и распаковки. Например, хотя процесс сжатия ошибки в вышеупомянутой схеме сжатия звука без потерь может быть описан как дельта-кодирование от приближенной звуковой волны до исходной звуковой волны, приближенная версия звуковой волны не имеет смысла ни в каком другом контексте. .
Методы сжатия без потерь
Ни один алгоритм сжатия без потерь не может эффективно сжать все возможные данные (подробности см. В разделе « Ограничения» ниже). По этой причине существует множество различных алгоритмов, которые разработаны либо с учетом конкретного типа входных данных, либо с конкретными предположениями о том, какие виды избыточности могут содержать несжатые данные.
Некоторые из наиболее распространенных алгоритмов сжатия без потерь перечислены ниже.
Общее назначение
Аудио
Растровая графика
- HEIF — высокоэффективный формат файлов изображений (сжатие без потерь или с потерями, с использованием HEVC )
- ILBM — (сжатие RLE без потерь изображений Amiga IFF )
- LDCT — дискретное косинусное преобразование без потерь
- JBIG2 — (сжатие без потерь или с потерями черно-белых изображений)
- JPEG 2000 — (включает метод сжатия без потерь через обратимое целочисленное вейвлет-преобразование LeGall-Tabatabai 5/3 )
- JPEG XR — ранее WMPhoto и HD Photo , включает метод сжатия без потерь
- JPEG-LS — (стандарт сжатия без / почти без потерь)
- PCX — Обмен PiCture
- PDF — Portable Document Format (сжатие без потерь или с потерями)
- PNG — переносимая сетевая графика
- TIFF — формат файла изображения с тегами (сжатие без потерь или с потерями)
- TGA — Truevision TGA
- WebP — (сжатие без потерь или с потерями изображений RGB и RGBA)
- FLIF — бесплатный формат изображений без потерь
- AVIF — формат файла изображения AOMedia Video 1
3D Графика
- OpenCTM — сжатие без потерь трехмерных треугольных сеток
видео
См. Этот список видеокодеков без потерь.
Криптография
Криптосистемы часто сжимают данные («открытый текст») перед шифрованием для дополнительной безопасности. При правильной реализации сжатие значительно увеличивает расстояние единственности за счет удаления шаблонов, которые могут облегчить криптоанализ . Однако многие обычные алгоритмы сжатия без потерь создают заголовки, оболочки, таблицы или другой предсказуемый вывод, который вместо этого может облегчить криптоанализ. Таким образом, криптосистемы должны использовать алгоритмы сжатия, выходные данные которых не содержат этих предсказуемых шаблонов.
Генетика и геномика
Алгоритмы сжатия генетики (не путать с генетическими алгоритмами ) — это последнее поколение алгоритмов сжатия без потерь, которые сжимают данные (обычно последовательности нуклеотидов) с использованием как обычных алгоритмов сжатия, так и специальных алгоритмов, адаптированных к генетическим данным. В 2012 году группа ученых из Университета Джона Хопкинса опубликовала первый алгоритм сжатия генетических данных, который не использует внешние генетические базы данных для сжатия. HAPZIPPER был адаптирован для данных HapMap и обеспечивает более чем 20-кратное сжатие (уменьшение размера файла на 95%), обеспечивая сжатие в 2–4 раза лучше, намного быстрее, чем ведущие универсальные утилиты сжатия.
Алгоритмы сжатия геномных последовательностей, также известные как компрессоры последовательностей ДНК, исследуют тот факт, что последовательности ДНК имеют характерные свойства, такие как инвертированные повторы. Наиболее успешными компрессорами являются XM и GeCo. Для эукариот XM немного лучше по степени сжатия, хотя для последовательностей размером более 100 МБ его вычислительные требования непрактичны.
Исполняемые файлы
Самораспаковывающиеся исполняемые файлы содержат сжатое приложение и декомпрессор. При запуске декомпрессор прозрачно распаковывает и запускает исходное приложение. Это особенно часто используется в демонстрационном кодировании, где проводятся соревнования для демонстраций со строгими ограничениями по размеру, до 1k . Этот тип сжатия не ограничивается строго двоичными исполняемыми файлами, но также может применяться к сценариям, таким как JavaScript .
Тесты сжатия без потерь
Алгоритмы сжатия без потерь и их реализации регулярно тестируются в прямых тестах . Есть ряд наиболее известных тестов сжатия. Некоторые тесты охватывают только степень сжатия данных , поэтому победители в этих тестах могут оказаться непригодными для повседневного использования из-за медленной скорости лучших исполнителей. Еще одним недостатком некоторых тестов является то, что их файлы данных известны, поэтому некоторые разработчики программ могут оптимизировать свои программы для достижения максимальной производительности на конкретном наборе данных. Победители в этих тестах часто приходят из класса программного обеспечения для сжатия контекста .
Мэтт Махони в своем выпуске бесплатного буклета « Объяснение сжатия данных» за февраль 2010 г. дополнительно перечисляет следующее:
- Корпус Калгари, построенный в 1987 году, больше не используется широко из-за своего небольшого размера. Мэтт Махони в настоящее время поддерживает программу Calgary Compression Challenge, созданную и поддерживаемую с 21 мая 1996 г. по 21 мая 2016 г. Леонидом Броухисом.
- Тестирование сжатия большого текста и аналогичный приз Hutter Prize используют обрезанный набор данных Wikipedia XML UTF-8 .
- Generic Compression Benchmark, поддерживаемый самим Махони, проверяет сжатие данных, генерируемых случайными машинами Тьюринга .
- Сами Рансас (автор NanoZip) поддерживает рейтинги сжатия, эталонный тест, аналогичный тесту максимального сжатия нескольких файлов, но с минимальными требованиями к скорости. Он также предлагает калькулятор, который позволяет пользователю взвесить важность скорости и степени сжатия. Топовые программы здесь довольно разные из-за требований к скорости. В январе 2010 года самыми популярными программами были NanoZip, за которыми следовали FreeArc , CCM , flashzip и 7-Zip .
- Тест Monster of Compression от NF Antonio тестирует сжатие 1 ГБ общедоступных данных с 40-минутным ограничением по времени. По состоянию на 20 декабря 2009 г. лучшим архиватором является NanoZip 0.07a, а лучшим компрессором для одиночных файлов — ccmx 1.30c, оба контекста смешиваются .
Веб-сайт Compression Ratings опубликовал сводную диаграмму «границы» по степени сжатия и времени.
Инструмент Compression Analysis Tool — это приложение для Windows, которое позволяет конечным пользователям оценивать характеристики производительности потоковых реализаций LZF4, DEFLATE, ZLIB, GZIP, BZIP2 и LZMA, используя свои собственные данные. Он производит измерения и диаграммы, с помощью которых пользователи могут сравнивать скорость сжатия, скорость распаковки и степень сжатия различных методов сжатия и проверять, как уровень сжатия, размер буфера и операции очистки влияют на результаты.
Ограничения
Алгоритмы сжатия данных без потерь не могут гарантировать сжатие для всех наборов входных данных. Другими словами, для любого алгоритма сжатия данных без потерь будет входной набор данных, который не станет меньше при обработке алгоритмом, а для любого алгоритма сжатия данных без потерь, который уменьшает хотя бы один файл, будет хотя бы один файл, который он увеличивает. Это легко доказать с помощью элементарной математики, используя следующий счетный аргумент :
- Предположим, что каждый файл представлен как строка бит произвольной длины.
- Предположим, что существует алгоритм сжатия, который преобразует каждый файл в выходной файл, длина которого не превышает длину исходного файла, и что по крайней мере один файл будет сжат в выходной файл, который короче исходного файла.
- Пусть M будет наименьшим числом, при котором существует файл F с длиной M бит, который сжимается до чего-то более короткого. Пусть N будет длина (в битах) сжатой версии F .
- Поскольку N < M , каждый файл длины N сохраняет свой размер во время сжатия. Таких файлов может быть 2 N. Вместе с F , это делает 2 N + 1 , что все файлы компресса в одном из 2 N файлов длины N .
- Но 2 N меньше, чем 2 N +1, поэтому по принципу «ящика» должен существовать некоторый файл длины N, который одновременно является выходом функции сжатия на двух разных входах. Этот файл не может быть надежно распакован (какой из двух оригиналов должен дать результат?), Что противоречит предположению о том, что алгоритм был без потерь.
- Следовательно, мы должны заключить, что наша исходная гипотеза (что функция сжатия больше не делает файл) обязательно неверна.
Любой алгоритм сжатия без потерь, который делает некоторые файлы короче, обязательно должен делать некоторые файлы длиннее, но необязательно, чтобы эти файлы становились намного длиннее. Большинство практических алгоритмов сжатия предоставляют возможность «избежать», которая может отключить нормальное кодирование файлов, которые стали бы длиннее из-за кодирования. Теоретически требуется только один дополнительный бит, чтобы сообщить декодеру, что нормальное кодирование отключено для всего ввода; однако в большинстве алгоритмов кодирования для этой цели используется по крайней мере один полный байт (а обычно более одного). Например, сжатые файлы DEFLATE никогда не должны увеличиваться более чем на 5 байтов на 65 535 байтов ввода.
Фактически, если мы рассмотрим файлы длины N, если бы все файлы были равновероятными, то для любого сжатия без потерь, которое уменьшает размер некоторого файла, ожидаемая длина сжатого файла (усредненная по всем возможным файлам длины N) обязательно должна быть больше N. Так что, если мы ничего не знаем о свойствах сжимаемых данных, мы могли бы вообще не сжимать их. Алгоритм сжатия без потерь полезен только тогда, когда мы с большей вероятностью сжимаем одни типы файлов, чем другие; тогда алгоритм может быть разработан для лучшего сжатия этих типов данных.
Таким образом, главный урок из этого аргумента заключается не в том, что человек рискует большими потерями, а просто в том, что нельзя всегда выигрывать. Выбор алгоритма всегда означает неявный выбор подмножества всех файлов, которые станут существенно короче. Это теоретическая причина, по которой нам нужны разные алгоритмы сжатия для разных типов файлов: не может быть никакого алгоритма, подходящего для всех типов данных.
«Уловка», которая позволяет алгоритмам сжатия без потерь, используемым для того типа данных, для которого они были разработаны, для последовательного сжатия таких файлов до более короткой формы заключается в том, что файлы, для которых предназначены алгоритмы, имеют некоторую форму легко моделируемой избыточности, которая алгоритм предназначен для удаления и, следовательно, относится к подмножеству файлов, которые этот алгоритм может сделать короче, тогда как другие файлы не будут сжиматься или даже увеличиваться. Алгоритмы, как правило, специально настроены для конкретного типа файла: например, программы сжатия звука без потерь плохо работают с текстовыми файлами, и наоборот.
В частности, файлы со случайными данными не могут быть последовательно сжаты с помощью любого мыслимого алгоритма сжатия данных без потерь: действительно, этот результат используется для определения концепции случайности в теории алгоритмической сложности .
Доказано, что невозможно создать алгоритм, который может без потерь сжать любые данные. Несмотря на то, что на протяжении многих лет было много заявлений о том, что компании достигли «идеального сжатия», когда произвольное количество N случайных битов всегда может быть сжато до N — 1 битов, такого рода заявления можно безопасно отбросить, даже не рассматривая какие-либо дополнительные детали, касающиеся предполагаемая схема сжатия. Такой алгоритм противоречит фундаментальным законам математики, потому что, если бы он существовал, его можно было бы многократно применять, чтобы без потерь уменьшить любой файл до нулевой длины. По этой причине якобы «идеальные» алгоритмы сжатия часто насмешливо называют «волшебными» алгоритмами сжатия.
С другой стороны, также было доказано, что не существует алгоритма для определения того, является ли файл несжимаемым в смысле колмогоровской сложности . Следовательно, возможно, что любой конкретный файл, даже если он выглядит случайным, может быть значительно сжат, даже включая размер декомпрессора. Примером могут служить цифры математической константы « пи» , которые кажутся случайными, но могут быть сгенерированы очень маленькой программой. Однако, хотя невозможно определить, является ли конкретный файл несжимаемым, простая теорема о несжимаемых строках показывает, что более 99% файлов любой заданной длины не могут быть сжаты более чем на один байт (включая размер декомпрессора).
Математический фон
Абстрактно алгоритм сжатия можно рассматривать как функцию от последовательностей (обычно октетов). Сжатие считается успешным, если результирующая последовательность короче исходной последовательности (и инструкций для карты декомпрессии). Чтобы алгоритм сжатия работал без потерь , карта сжатия должна формировать инъекцию от «простых» до «сжатых» битовых последовательностей.
Принцип голубятни запрещает взаимное соответствие между набором последовательностей длины N и любым подмножеством набора последовательностей длины N -1. Следовательно, невозможно создать алгоритм без потерь, который уменьшал бы размер каждой возможной входной последовательности.
Точки применения в реальной теории сжатия
Разработчики реальных алгоритмов сжатия признают, что потоки с высокой энтропией информации не могут быть сжаты, и, соответственно, включают средства для обнаружения и обработки этого условия. Очевидный способ обнаружения — применение алгоритма необработанного сжатия и проверка того, меньше ли его выход, чем вход. Иногда обнаружение осуществляется эвристикой ; например, приложение сжатия может считать файлы, имена которых заканчиваются на «.zip», «.arj» или «.lha», несжимаемыми без какого-либо более сложного обнаружения. Распространенный способ справиться с этой ситуацией — цитировать ввод или несжимаемые части ввода в выводе, минимизируя накладные расходы на сжатие. Например, формат данных zip определяет «метод сжатия» «Сохранено» для входных файлов, которые были дословно скопированы в архив.
Испытание на миллион случайных цифр
Марк Нельсон, в ответ на утверждения о магических алгоритмах сжатия, появляющихся в comp.compression, сконструировал двоичный файл размером 415 241 байт с высокоэнтропийным содержимым и бросил публичный вызов в 100 долларов каждому, кто бы мог написать программу, которая вместе с входными данными могла бы быть меньше, чем предоставленные им двоичные данные, но иметь возможность восстановить их без ошибок.
FAQ для comp.compression телеконференции содержит вызов Майка Голдман предлагают $ 5000 за программу , которая может сжимать случайные данные. Патрик Крейг принял вызов, но вместо того, чтобы сжимать данные, он разделил их на отдельные файлы, все из которых оканчивались цифрой 5 , которая не хранилась как часть файла. Отсутствие этого символа позволяло результирующим файлам (плюс, в соответствии с правилами, размеру программы, которая их собирала повторно) быть меньше, чем исходный файл. Однако фактического сжатия не было, и информация, хранящаяся в именах файлов, была необходима для их повторной сборки в правильном порядке в исходном файле, и эта информация не была принята во внимание при сравнении размеров файлов. Таким образом, самих файлов недостаточно для восстановления исходного файла; имена файлов также необходимы. Патрик Крейг согласился с тем, что никакого значимого сжатия не произошло, но утверждал, что формулировка возражения на самом деле этого не требует. Полная история мероприятия, включая обсуждение того, была ли проблема решена технически, находится на веб-сайте Патрика Крейга.
Смотрите также
Ссылки
дальнейшее чтение
- Сайуд, Халид (2017-10-27). Введение в сжатие данных . Серия Морган Кауфманн в мультимедийной информации и системах (5 — е изд.). Морган Кауфманн . ISBN 978-0-12809474-7. (790 стр.)
- Сайуд, Халид, изд. (2002-12-18). Справочник по сжатию без потерь (коммуникации, сети и мультимедиа) (1-е изд.). Академическая пресса . ISBN 978-0-12390754-7. (488 стр.)
внешние ссылки
Методы сжатия данных | Статья в журнале «Молодой ученый»
В рамках этой работы было проведено исследование проблематики сохранения качества цифровой информации при использовании метода сжатия данных Хаффмана. В этой работе была полностью описана специфика этого метода, вместе с его основными преимуществами.
Ключевые слова:
цифровые данные, информация, методика сжатия цифровой информации, метод сжатия Хаффмана, методик сжатия информации без потери качества.
Стоит отметить, что современный мир остро нуждается в разработке и практическом использовании продвинутых методов сжатия цифровой информации. Конечно, сейчас человечество имеет доступ не только к хранилищам цифровых данных огромного объема, но и к высокоскоростным способам обмена информацией. При этом, нужно учесть, что постоянно наблюдается рост объемов передачи данных. Ранее вполне нормальным было смотреть фильмы, записанные на обычном компакт-диске, вмещающем в себя 700 мегабайт информации. Теперь же при просмотре онлайн-фильмов в высоком качестве, видеоряд может занимать несколько десятков гигабайт пространства. Безусловно для обеспечения возможности хранения такого огромного объема информации и ее передачи потребуется не только время и широкий канал передачи информации, но и большое хранилище цифровых данных. Для реализации этих задач как раз-таки и применяются различные методики сжатия информации. В рамках этой статьи будет изучен принцип работы методов сжатия цифровой информации без потери ее качества. Также мы попробуем понять, как работает самый популярный метод сжатия данных под названием «алгоритм Хаффмана».
Процесс сжатия объема цифровой информации имеет выраженный алгоритмический характер. Он основан на принципе сокращение избыточности объемов данных. Метод сжатия информации предполагает уменьшение ее объема без ее утери. [1, с. 214]
В основе алгоритма Хаффмана лежит элементарная концепция. В рамках этого алгоритма применяется метод, предполагающий кодирование одинаковых символом меньшим количеством бит, чем тех символов, что встречаются не так часто.
Подобный метод сжатия цифровой информации был разработан в 1952 году Д. А. Хаффманом. При этом в то время еще не было никаких компьютеров современного типа. За счет эффективности этого метода он был положен в различные современные способы сжатия цифровых данных путем применения специальных кодировочных алгоритмов.
В основе идеи алгоритма лежит следующий принцип: при наличии знаний о вероятности наличия в сообщении конкретных символов, возникает возможность описания формирования кодов с переменной длиной, которые будут структурно представлять собой цельные количества битов. Короткие коды присваиваются тем символам, которые встречаются чаще. У кодов Хаффмана есть свой индивидуальный префикс, что дает возможность их декодировки даже несмотря на то, что их длина имеет переменный характер.
При использовании динамического алгоритма, разработанного Хаффманом, можно будет получить на входе частотную таблицу символов, которые встречаются в конкретном сообщении. На следующем этапе на основе данной таблицы происходит построение кодировочного дерева Хаффмана.
На сегодняшний день применяются два способа сжатия цифровой информации: с потерями части данных и без каких-либо потерь. При использовании метода сжатия информации с потерями восстановленная информация будет несколько отличаться от изначальной, что приводит к падению ее качества. Этот способ применим в тех случаях, когда при восстановлении цифровой информации не требуется максимальная точность. Если же используется способ сжатия без потерь, тогда восстановленные данные будут иметь свой исходный вид. Подобный метод, как правило, применяется при передачи текстовых цифровых документов. В дальнейшем в рамках этой работы будет проводиться работа по изучению второго способа сжатия цифровой информации. [2, с. 364]
Методика сжатия цифровой информации без потерь использует алгоритм уменьшения битов за счет определения и последующего удаления обнаруженной избыточности статистического характера. Для того, чтоб понять принцип работы этого способа, потребуется ознакомиться с некоторыми следующими примерами. [4, с. 163]
Предположим, у нас есть набор из девяти фигур круглой формы. Три красных, три голубых и три коричневых круга. При этом, вместо того, чтоб показывать все девять кругов можно просто оставить три круга разного цвета и указать рядом с ними количество этих кругов. Фактически, мы предоставляем аналогичную информацию, но уже меньшего объема.
В качестве еще одного примера можно взять файл, содержащий в себе следующий текст: RRRRRZZZZEEEGGGGGG.
Данная текстовая информация с помощью методики Хаффмана может быть сжата следующим образом: R5Z4E3G6. В итоге вместо 18 символов нам для предоставления аналогичной информации потребовалось всего 8. При этом, может показаться, что этот метод сжатия данных работает слишком безукоризненно, что сложно себе представить. По сути, во многом, сама концепция сжатия информации без потерь, идет в разрез Ньютоновским физическим законам.
Правда, все же этот метод действительно идеально работает. Современные программы, использующиеся для сжатия информации без потерь, обеспечивают это за счет использования таких эффективных алгоритмов, как алгоритм Хаффмана, а также кодирование LZW. [4, с. 241]
Особенности алгоритма Хаффмана
В основе популярности этого метода сжатия цифровой информации лежит его простота и легкость применения. Несмотря на то, что сама методика была придумана еще в середине 20-го века, она до сих пор сохраняет свою актуальность. В основе работы алгоритма Хаффмана лежит принцип того, что в цифровой информации одни символы могут встречаться намного чаще других. При этом потребуется найти самые часто встречающиеся символы и присвоить ими короткую кодировку. При этом самые редкие символы получают, наоборот, длинный код. В рамках алгоритма Хаффмана на входе должна находиться изначально сформированная частотная таблица, без которой сам метод попросту не будет работать. [2, с. 75]
Алгоритм сжатия информации задается частотной таблицей. Изначально определяется пара информационных узлов с самой низкой частотой символов. После этого формируется родитель, который будет равен сумме частот. При этом родитель будет выступать в качестве нового полноценного узла, который придет на замену двум предыдущим узлам. Дуге, выходящей от родителя, присваивается бит с нулем или единицей. Данная операция повторно осуществляется до момента пока внутри списка не будет сформирован один единственный узел. К примеру, мы имеем следующую частотную табличку:
Исходя из специфики используемого алгоритма, потребуется провести работу по суммированию пары узлов, имеющих самую низкую частотность:
. Новый родитель G/H будет получен из G и H. При этом узлы, являющиеся прародителями родителя, будут удалены. После этого самым меньшим частотным весом будут обладать узлы G/H и F. После суммирования узлов формируется новый родитель с их удалением. Данные манипуляции осуществляются до того самого момента, когда останется всего лишь один единственный узел. Само кодировочное дерево будет иметь следующий вид:
На следующем этапе каждому символу присваивается уникальный код. Для этой цели нужно будет продвигаться по направлению снизу вверх по кодировочному древу. При этом нужно будет копить биты в процессе движения по веткам древа. Движение вправо это ноль бит, а влево один бит. В итоге на выходе будет получена таблица следующего вида:
У этого алгоритма есть один серьезный недостаток, заключающийся в том, что декодеру для восстановления информации нужно будет иметь данные о частотной таблице. В итоге размер полученного файла будет увеличен по причине размещения перед кодом частотной таблицы. Также нужно отметить, что факт наличия полноценной частотной таблицы Кроме того, факт наличия перед кодировочным кодом полноценной частотной таблицы диктует необходимость двойной проходки по сообщению с целью формирования самой модели информации и для ее последующего декодирования. [5, с. 152]
Несмотря на то, что алгоритм Хаффмана был разработан более 60 лет назад, он до сих пор сохранил свою актуальность. Поэтому он в том или ином виде используется современными программами, обеспечивающими возможность сжатия данных без их потери.
В рамках данной статьи была проведена работа по описанию способов сжатия цифровой информации без ее потери, а также был описан самый популярный алгоритм Хаффмана. При этом, важно отметить, что существуют самые разные алгоритмы, обеспечивающие возможность сжатия данных без потерь. Поэтому пользователю нужно будет самостоятельно выбирать наиболее подходящий для себя способ.
Литература:
- Баринов В. В. Сжатие данных, речи, звука и изображений в телекоммуникационных системах, РадиоСофт — Москва, 2019. — 360 c.
- Вотолин Д. Ратушпяк А. Смирнов М. Юкин В. Методы сжатия данных. Устройство архиваторов, Сжатие изображений и видео. — М.:ДИАЛОГ-МИФИ, 2018 г. — 381 с.
- Рассел Джесси Сжатие данных, Книга по Требованию — Москва, 2017. — 104 c.
- Ратушняк О. А. Сжатие мультимедийной информации. // Hard’n’Soft. 2016. — №.4 — стр. 78–79.
- Сэломон Д. Сжатие данных, изображений и звука, Техносфера — Москва, 2016. — 368 c.
Основные термины (генерируются автоматически): цифровая информация, потеря, рамка этой, символ, частотная таблица, LZW, RRRRRZZZZEEEGGGGGG, алгоритм Хаффмана, единственный узел, полноценная частотная таблица.
Методы сжатия изображений | Статья в журнале «Молодой ученый»
В данной работе рассмотрены основные виды избыточности графической информации, а также способы ее устранения. В результате сжатия уменьшается размер изображения, что сокращает время передачи изображения по сети, и экономит пространство для хранения.Все большую актуальность приобретают эффективные методы сжатия, влекущие за собой наименьшие потери данных.
Ключевые слова: сжатие изображений, избыточность информации, кодирование, кодер, декодер.
Ежедневно огромное количество информации запоминается, преобразуется и передается в цифровом виде. Поскольку большая часть передаваемых данных является графической или видеоинформацией, возникает все большая потребность в качественном сжатии, влекущем за собой как можно меньшие потери. Сжатие изображений ориентировано на сокращение объема данных представляющих определенное количество информации. Зачастую эта проблема решается путем удаления избыточной информации.
Пусть и обозначают число элементов (носителей информации) в двух наборах данных, представляющих одну и ту же информацию. Тогда относительная избыточность данных может быть определена как
,
где называется коэффициентом сжатия и вычисляется как
.
Различают три вида избыточности данных в задаче цифрового сжатия изображений: кодовая, межэлементная и визуальная избыточность. Сжатие данных достигается в том случае, когда устраняется или сокращается избыточность одного или нескольких из вышеуказанных видов. Рассмотрим каждый из видов по отдельности [1].
Пусть дискретная случайная переменная появляется с вероятностью , – общее число уровней яркости,– число пикселей, имеющих значение яркости , а – общее число элементов в изображении. Если число битов, используемых для представления каждого из значений , равно , то среднее число битов, требуемых для представления значения одного элемента, равно:
т. е. средняя длина всех кодовых слов, присвоенных различным значениям яркостей, определяется как сумма произведений числа битов, используемых для представления каждого из уровней яркостей на вероятность появления этого уровня яркости.
Если код значения яркости образуется не минимизацией предыдущего уравнения, то говорят, что изображение имеет кодовую избыточность. Нетрудно увидеть, что присвоение кодовых слов с меньшим числом битов более вероятным значениям яркости, и наоборот, более длинных кодовых слов менее вероятным значениям т. е. применение неравномерного кодирования, позволяет достичь сжатия данных.
С другой стороны, кодирование, используемое для представления значений яркости, не может изменить корреляции между пикселями, которая является следствием структурных или геометрических взаимосвязей между объектами на изображении. Коэффициенты автокорреляции , вычисленные вдоль одной строки каждого изображения могут быть получены с помощью уравнения:
,
где
Поскольку значение каждого элемента изображения может быть предсказано по значениям его соседних, то информация, содержащаяся в отдельном элементе, оказывается достаточно малой. Большая часть содержащейся информации является избыточной. Такая избыточность называется межэлементной. Для ее уменьшения двумерный массив пикселей должен быть преобразован в некоторый более рациональный формат. Другими словами, нужно найти отображение данного множества в более упрощенное, достигнутое, допустим, разностью между соседними пикселями.
Известно, что воспринимаемая глазом яркость зависит не только от количества света, исходящего из рассматриваемой области. При обычном визуальном восприятии часть информации оказывается менее важной, чем другая. Такую информацию называют визуально избыточной. Она может быть удалена без заметного ухудшения визуального качества изображения [1,2,3].
Рассмотренные выше методы избавления от разных видов избыточности информации на практике обычно используются совместно. Система сжатия любого изображения состоит из двух структурных блоков: кодер и декодер. Исходное изображение поступает на вход кодера, который преобразует его в набор символов. После передачи по каналу данные поступают в декодер, где создается восстановленное изображение . В результате может получиться как точная копия исходного изображения (кодирование без потерь), так и несколько измененная (кодированная с потерями)
Рис. 1. Общая модель системы сжатия
Кодер источника сокращает возможные виды избыточности на входном изображении. Благодаря отдельным приложениям выбирается тот или иной способ шифрования, являющийся оптимальным в каждом конкретном случае. Процедура кодирования представляется в виде последовательности трех стадий: преобразователь, квантователь и кодер символов. На этапе преобразователя входные данные (изображение) представляется в формате, предназначенном для сокращения межэлементной избыточности. Второй шаг, или блок квантователя, позволяет сократить визуальную избыточность за счет уменьшения точности выхода преобразователя. На третьей и последней стадии кодер символов создает равномерный или неравномерный код. Таким образом, после прохождения трех этапов кодирования изображение избавляется от всех видов избыточности. Однако, следует помнить, что этап квантователя является необратимым, что в случае сжатия без потерь требует пропуска этого шага [4,6].
Схема декодера источника включает лишь два блока: декодер символов и обратный преобразователь. Здесь осуществляются операции, обратные тем операциям, которые выполнялись в кодере источника, причем в обратном порядке, исключая лишь этап квантователя, по той же причине его необратимости.
В случае, когда канал передачи имеет собственные шумы и помехи, важную роль в процессе кодирования играют кодер и декодер канала. Уменьшение влияния шума в канале передачи достигается путем наращивания к исходным закодированным данным избыточной информации. К слову добавляются проверочные биты, способные исправить и обнаружить единичные ошибки. Этот прием позволяет добиться большей устойчивости передаваемым данным к помехам. Декодер канала, аналогично декодеру источника выполняет обратные преобразования.
Алгоритмы сжатия изображений подразделяются на две большие группы: без потерь и с потерями. Первые в ходе передачи сохраняют информацию об изображении полностью, а вторые — только частично. Первая группа методов сжатия обеспечивает восстановление исходного изображения без потерь и искажений. К изображениям, предназначенным для хранения с целью дальнейшей обработки, следует применять методы первого типа. Однако, если изображение предназначено для визуального восприятия, это не всегда необходимо. В ряде случаев исходный сигнал уже содержит такие искажения и шумы, что небольшие потери информации при кодировании (в пользу высокой степени сжатия) не испортят качества изображения в целом [5].
Одна из серьезных проблем компьютерной графики заключается в том, что до сих пор не найден адекватный и однозначный критерий оценки потерь качества изображения. Для изображений, наблюдаемых визуально, основным является неотличимость глазом исходного и компрессированного изображения.
При передаче сжатых данных неизбежно возникают потери. Однако в некоторых отдельных случаях такое положение вещей недопустимо. Одним из примеров может служить архивация медицинских и деловых документов, сжатие с потерями которых зачастую запрещено законом. Другим примером являются спутниковые изображения, способ получения которых слишком дорогостоящ, для того, чтобы производить сжатие с потерями. Таким образом, сжатие изображения без потерь всегда будет достаточно востребовано. Алгоритмы такого сжатия обычно состоят из двух не зависящих друг от друга операций: разработка альтернативного представления изображения, в котором уменьшена межэлементная избыточность, и кодирование полученных данных для устранения кодовой избыточности [1]. К наиболее распространенным подходам сжатия без потерь относятся: неравномерное кодирование (кодирование Хаффмана, кодирование с помощью почти оптимальных неравномерных кодов, арифметическое кодирование), LZW кодирование, кодирование битовых плоскостей, кодирование без потерь с предсказанием.
Сжатие с потерями основано на выборе баланса между точностью восстановления изображения и степенью его сжимаемости. Если можно допустить появление некоторого искажения в конечном результате кодирования, то возможно значительное увеличение коэффициента сжатия. Как показано выше, принципиальная разница между структурными схемами двух подходов заключается в наличии или отсутствии блока квантования. Различают следующие виды сжатия с потерями: кодирование с предсказаниями, трансформационное кодирование, вейвлет-кодирование [6].
В данной статье мы изложили теоретические основы сжатия цифровых изображений, а также описали наиболее распространенные методы сжатия, составляющие ядро существующей на данный момент технологии. Предложенные методы играют все более важную роль в архивном хранении изображений документов, в также при передаче данных. Наряду с обработкой изображений, сжатие является высоко перспективной областью, что гарантирует дальнейшее развитие имеющихся методов и стандартов [1].
Литература:
- Гонсалес Р., Вудс Р. Цифровая обработка сигналов //М.: Техносфера. — 2005.
- Смит С. Цифровая обработка сигналов. — М.: Додэка-XXI, 2008.
- Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов (1984 ориг.). — Мир, 1988.
- Белоусов А. А., Спицын В. Г. Двухэтапный метод улучшения изображений. — 2009.
- Poynton C. A. A technical introduction to digital video. — John Wiley & Sons, Inc., 1996.
- Gonzalez R. C., Woods R. E., Eddins S. L. Digital image processing using MATLAB. — Pearson Education India, 2004
Основные термины (генерируются автоматически): потеря, изображение, исходное изображение, кодирование, LZW, визуальная избыточность, избыточная информация, кодовая избыточность, межэлементная избыточность, неравномерное кодирование.
Выбор метода сжатия
WinZip ® предоставляет несколько методов сжатия файлов, которые вы добавляете в Zip-файл. При выборе методов сжатия необходимо учитывать несколько факторов, в том числе тип данных, которые вы сжимаете, ваши планы на последующее разархивирование данных и время, в течение которого вы готовы подождать, пока ваши данные сжимаются.
Использование ленточного интерфейса WinZip
В интерфейсе ленты WinZip вам нужно будет выбрать соответствующий метод сжатия, который будет использоваться до начала процесса архивирования.
Установка метода сжатия выполняется на вкладке Настройки ленты WinZip. Установите соответствующий метод сжатия в полях .Zip и .Zipx , которые будут использоваться при создании файлов .zip или .zipx соответственно.
Более подробную информацию о каждом из методов сжатия см. В разделе Дополнительная информация о конкретных методах сжатия ниже.
Дополнительная информация о конкретных методах сжатия
Вот дополнительная информация обо всех методах сжатия, поддерживаемых текущей версией WinZip:
Нет или Без сжатия
Некоторые файлы, которые вы можете добавить в Zip-файл, уже сжаты.Например, многие мультимедийные и звуковые файлы, такие как файлы avi и MP3, представляют собой предварительно сжатые версии изображений и звука. В большинстве случаев эти типы файлов не могут быть в значительной степени сжаты доступными методами. Поэтому для экономии времени лучше выбрать Нет или Нет сжатия , когда вы добавляете группу файлов, которые уже сжаты.
SuperFast
Это хороший универсальный алгоритм сжатия, известный как «deflate».Это тот же базовый алгоритм, который используется для сжатия Legacy (см. Выше), но он оптимизирован по скорости, а не по размеру сжатия. Поэтому он обычно сжимает ваши файлы несколько быстрее, чем Legacy , но сжатые файлы будут несколько больше.
Более ранние версии WinZip поддерживали четыре варианта алгоритма дефлятирования, которые назывались Максимум (переносимый) , Fast , SuperFast и Нормальный . Все они использовали одну и ту же базовую технологию, но были по-разному оптимизированы по скорости и скорости.сжатие. WinZip 12 и более поздние версии больше не используют Fast и Normal при сжатии файлов, но по-прежнему могут извлекать файлы, сжатые любым из этих методов.
Улучшенный спуск
Метод «расширенной дефляции» похож на исходную дефляцию, но работает с большими порциями данных за раз, что часто приводит к улучшенному сжатию. Это может быть особенно полезно для сжатия больших файлов, содержащих большие объемы данных с высокой степенью сжатия, таких как большие текстовые файлы и текстовые файлы баз данных.
В более ранних версиях WinZip этот метод сжатия назывался Максимум (расширенное сжатие) .
bzip2
bzip2 — это алгоритм сжатия данных с открытым исходным кодом, который сжимает большинство файлов более эффективно, чем традиционные методы deflate, но может быть несколько медленнее.
В более ранних версиях WinZip этот метод сжатия именовался как Максимум (bzip2) .
LZMA
LZMA — это метод сжатия данных с открытым исходным кодом, который использует схему сжатия словаря, которая использует больший размер словаря, чем метод deflate.Он может обеспечить более высокую степень сжатия, чем старые методы.
частей на миллион
PPMd — это алгоритм сжатия данных с открытым исходным кодом, который может сжимать большинство текстовых данных более эффективно, чем традиционный метод deflate или bzip2, но который довольно часто работает медленнее, чем любой другой.
В более ранних версиях WinZip этот метод сжатия именовался как Максимум (PPMd) .
XZ
XZ — это метод сжатия данных с открытым исходным кодом, в котором используется алгоритм LZMA2 для получения более высокой степени сжатия.
Jpeg сжатие
Метод сжатия Jpeg разработан для сжатия изображений JPEG. Изображения JPEG по своей сути сложно сжимать, потому что их формат уже включает простую, но эффективную схему сжатия. На высоком уровне сжатие Jpeg работает, сначала отменяя сжатие без потерь (энтропийное кодирование) в изображениях JPEG, а затем повторно сжимая их с помощью лучшего алгоритма. Когда изображение не сжато, происходит обратное: алгоритм сжатия Jpeg отменяется и повторно применяется исходное энтропийное кодирование JPEG.
| Сжатие JPEG нельзя выбрать вручную. Вместо этого WinZip будет автоматически использовать его при необходимости, если вы выберете «Лучший способ». |
WAVPACK
WAVPACK — это метод сжатия с открытым исходным кодом, специально разработанный для сжатия без потерь файлов .WAV (аудио). Для этих файлов он обычно обеспечивает лучшее сжатие, чем другие методы сжатия, поддерживаемые WinZip.
| Сжатие WAVPACK нельзя выбрать вручную. Вместо этого WinZip будет автоматически использовать его при необходимости, если вы выберете «Лучший способ». |
Сжатие MP3
Сжатие MP3 предназначено для сжатия аудиофайлов MP3. Для этих файлов он обычно обеспечивает лучшее сжатие, чем другие методы сжатия, поддерживаемые WinZip.
| Сжатие MP3 не может быть выбрано вручную.Вместо этого WinZip будет автоматически использовать его при необходимости, если вы выберете «Лучший способ». |
метод сжатия — это … Что такое метод сжатия?
Компрессионное формование — Резиновые сапоги, изготовленные методом компрессионного формования, до снятия заусенцев. Компрессионное формование — это метод формования, при котором формовочный материал, как правило, предварительно нагретый, сначала помещается в открытую нагретую полость формы. Форма закрывается с максимальным усилием или…… Wikipedia
Степень сжатия — Для получения информации о степени сжатия при сжатии данных см. Степень сжатия данных.Степень сжатия двигателя внутреннего сгорания или двигателя внешнего сгорания — это величина, которая представляет собой отношение объема его камеры сгорания к его…… Wikipedia
метод — Режим или способ или упорядоченная последовательность событий процесса или процедуры. СМОТРИ ТАКЖЕ: фиксатор, операция, процедура, краситель, техника. [ГРАММ. методики; фр. мета, после, + ходос, путь] Абель Кендалл м. а… Медицинский словарь
компрессионное формование — метод формования, при котором сжатие используется для уплотнения материала в форме и выражения его избытка из формы… Медицинский словарь
компрессионное формование — метод формования термореактивного пластика путем закрытия формы на нем, формование материала под действием тепла и давления.[1935 40] * * *… Универсал
сжатие — UK [kəmˈpreʃ (ə) n] / US имя существительное [бесчисленное множество] 1) процесс нажатия или сжатия чего-либо, чтобы оно стало меньше 2) вычисление метода уменьшения размера компьютерного файла, например чтобы на компьютере было меньше места… Английский словарь
компрессионное формование — существительное: процесс формования, используемый особенно для пластмасс, в котором тепло и давление воздействуют на материал в форме * * * метод формования термореактивного пластика путем закрытия формы на нем, формируя материал теплом и давлением.…… Полезный английский словарь
Сжатие данных без потерь — это класс алгоритмов сжатия данных, который позволяет восстанавливать точные исходные данные из сжатых данных. Термин «без потерь» отличается от сжатия данных с потерями, которое позволяет лишь приблизительно оценить исходные данные…… Wikipedia
Фрактальное сжатие — это метод сжатия изображений с потерями, использующий фракталы для достижения высокого уровня сжатия.Этот метод лучше всего подходит для фотографий природных пейзажей (деревья, горы, папоротники, облака). Техника фрактального сжатия основана на том, что в…… Wikipedia
Сжатие данных — Исходное кодирование перенаправляется сюда. Чтобы узнать о термине в компьютерном программировании, см. Исходный код. В информатике и теории информации сжатие данных, кодирование источника или уменьшение скорости передачи данных — это процесс кодирования информации с использованием меньшего количества бит, чем…… Wikipedia
Сжатие изображений — это приложение сжатия данных на цифровых изображениях.Фактически, цель состоит в том, чтобы уменьшить избыточность данных изображения, чтобы иметь возможность хранить или передавать данные в эффективной форме. Сжатие изображения может быть с потерями или без потерь. Без потерь…… Википедия
метод сжатия — это … Что такое метод сжатия?
Компрессионное формование — Резиновые сапоги, изготовленные методом компрессионного формования, до снятия заусенцев. Компрессионное формование — это метод формования, при котором формовочный материал, как правило, предварительно нагретый, сначала помещается в открытую нагретую полость формы.Форма закрывается с максимальным усилием или…… Wikipedia
Степень сжатия — Для получения информации о степени сжатия при сжатии данных см. Степень сжатия данных. Степень сжатия двигателя внутреннего сгорания или двигателя внешнего сгорания — это величина, которая представляет собой отношение объема его камеры сгорания к его…… Wikipedia
метод — Режим или способ или упорядоченная последовательность событий процесса или процедуры. СМОТРИ ТАКЖЕ: фиксатор, операция, процедура, краситель, техника.[ГРАММ. методики; фр. мета, после, + ходос, путь] Абель Кендалл м. а… Медицинский словарь
компрессионное формование — метод формования, при котором сжатие используется для уплотнения материала в форме и выражения его избытка из формы… Медицинский словарь
компрессионное формование — метод формования термореактивного пластика путем закрытия формы на нем, формование материала под действием тепла и давления. [1935 40] * * *… Универсал
сжатие — UK [kəmˈpreʃ (ə) n] / US имя существительное [бесчисленное множество] 1) процесс нажатия или сжатия чего-либо, чтобы оно стало меньше 2) вычисление метода уменьшения размера компьютерного файла, например чтобы на компьютере было меньше места… Английский словарь
компрессионное формование — существительное: процесс формования, используемый особенно для пластмасс, в котором тепло и давление воздействуют на материал в форме * * * метод формования термореактивного пластика путем закрытия формы на нем, формируя материал теплом и давлением.…… Полезный английский словарь
Сжатие данных без потерь — это класс алгоритмов сжатия данных, который позволяет восстанавливать точные исходные данные из сжатых данных. Термин «без потерь» отличается от сжатия данных с потерями, которое позволяет лишь приблизительно оценить исходные данные…… Wikipedia
Фрактальное сжатие — это метод сжатия изображений с потерями, использующий фракталы для достижения высокого уровня сжатия.Этот метод лучше всего подходит для фотографий природных пейзажей (деревья, горы, папоротники, облака). Техника фрактального сжатия основана на том, что в…… Wikipedia
Сжатие данных — Исходное кодирование перенаправляется сюда. Чтобы узнать о термине в компьютерном программировании, см. Исходный код. В информатике и теории информации сжатие данных, кодирование источника или уменьшение скорости передачи данных — это процесс кодирования информации с использованием меньшего количества бит, чем…… Wikipedia
Сжатие изображений — это приложение сжатия данных на цифровых изображениях.Фактически, цель состоит в том, чтобы уменьшить избыточность данных изображения, чтобы иметь возможность хранить или передавать данные в эффективной форме. Сжатие изображения может быть с потерями или без потерь. Без потерь…… Википедия
Сжатие данных
«Исходное кодирование» перенаправляется сюда. Чтобы узнать о термине в компьютерном программировании, см. Исходный код.
В информатике и теории информации, сжатие данных , кодирование источника или снижение скорости передачи данных — это процесс кодирования информации с использованием меньшего количества битов, чем использовалось бы в исходном представлении.
Сжатие полезно, поскольку помогает снизить потребление дорогостоящих ресурсов, таких как место на жестком диске или пропускная способность передачи. С другой стороны, для использования сжатые данные необходимо распаковать, и эта дополнительная обработка может нанести ущерб некоторым приложениям. Например, схема сжатия для видео может потребовать дорогостоящего оборудования для достаточно быстрой декомпрессии видео, чтобы его можно было просматривать во время декомпрессии (возможность полной распаковки видео перед его просмотром может быть неудобной и требует места для хранения распакованное видео).Таким образом, разработка схем сжатия данных включает компромисс между различными факторами, включая степень сжатия, величину вносимого искажения (при использовании схемы сжатия с потерями) и вычислительные ресурсы, необходимые для сжатия и распаковки данных. Сжатие было одним из основных драйверов роста информации в течение последних двух десятилетий [1] .
Сравнение сжатия без потерь и сжатия с потерями
Основные статьи: сжатие данных без потерь и сжатие данных с потерями
Алгоритмы сжатия без потерь обычно используют статистическую избыточность таким образом, чтобы представить данные отправителя более кратко и без ошибок.Сжатие без потерь возможно, потому что большинство реальных данных имеют статистическую избыточность. Например, в английском тексте буква «е» встречается гораздо чаще, чем буква «z», и вероятность того, что за буквой «q» будет следовать буква «z», очень мала. Другой вид сжатия, называемый сжатием данных с потерями, или перцепционным кодированием, возможен, если допустима некоторая потеря точности. Как правило, сжатие данных с потерями будет основываться на исследованиях того, как люди воспринимают эти данные.Например, человеческий глаз более чувствителен к незначительным изменениям яркости, чем к изменениям цвета. Сжатие изображений JPEG отчасти «округляет» часть этой менее важной информации. Сжатие данных с потерями позволяет получить наилучшую точность при заданной степени сжатия.
С потерей
Сжатие изображений с потерями используется в цифровых камерах для увеличения емкости памяти с минимальным ухудшением качества изображения. Точно так же DVD используют видеокодек MPEG-2 с потерями для сжатия видео.
При сжатии звука с потерями используются методы психоакустики для удаления неслышимых (или менее слышимых) компонентов сигнала. Сжатие человеческой речи часто выполняется с помощью даже более специализированных методов, поэтому «сжатие речи» или «кодирование голоса» иногда выделяют как отдельную дисциплину от «сжатия звука». Различные стандарты сжатия звука и речи перечислены в разделе «Аудиокодеки». Сжатие голоса используется, например, в интернет-телефонии, тогда как сжатие звука используется для копирования компакт-дисков и декодируется аудиоплеерами.
без потерь
Методы сжатия Лемпеля – Зива (LZ) — одни из самых популярных алгоритмов хранения без потерь. DEFLATE — это вариант LZ, который оптимизирован для скорости декомпрессии и степени сжатия, но сжатие может быть медленным. DEFLATE используется в PKZIP, gzip и PNG. LZW (Lempel – Ziv – Welch) используется в изображениях GIF. Также заслуживают внимания методы LZR (LZ – Renau), которые служат основой метода Zip. В методах LZ используется модель сжатия на основе таблиц, в которой записи таблицы заменяются повторяющимися строками данных.Для большинства методов LZ эта таблица создается динамически из более ранних данных во входных данных. Сама таблица часто закодирована по Хаффману (например, SHRI, LZX). Текущая хорошо работающая схема кодирования на основе LZ — это LZX, используемый в формате Microsoft CAB.
Самые лучшие современные компрессоры без потерь используют вероятностные модели, такие как прогнозирование путем частичного сопоставления. Преобразование Барроуза – Уиллера также можно рассматривать как косвенную форму статистического моделирования.
При дальнейшем усовершенствовании этих методов статистические предсказания могут быть объединены с алгоритмом, называемым арифметическим кодированием.Арифметическое кодирование, изобретенное Йормой Риссанен и превращенное в практический метод Виттеном, Нилом и Клири, обеспечивает превосходное сжатие по сравнению с более известным алгоритмом Хаффмана и особенно хорошо подходит для задач адаптивного сжатия данных, где прогнозы сильно зависят от контекста. зависимый. Арифметическое кодирование используется в стандарте двухуровневого сжатия изображений JBIG и стандарте сжатия документов DjVu. Текст запись система, Dasher, является кодировщиком обратной арифметики.
Теория
Теоретическая основа сжатия обеспечивается теорией информации (которая тесно связана с алгоритмической теорией информации) для сжатия без потерь и теорией скорости-искажения для сжатия с потерями.Эти области исследований были созданы Клодом Шенноном, опубликовавшим фундаментальные статьи по этой теме в конце 1940-х — начале 1950-х годов. Теория кодирования тоже связана. Идея сжатия данных глубоко связана со статистическим выводом.
Машинное обучение
Существует тесная связь между машинным обучением и сжатием: система, которая предсказывает апостериорные вероятности последовательности с учетом всей ее истории, может использоваться для оптимального сжатия данных (с помощью арифметического кодирования выходного распределения), в то время как оптимальный компрессор может быть используется для прогнозирования (путем нахождения символа, который сжимает лучше всего с учетом предыдущей истории).Эта эквивалентность использовалась в качестве оправдания для сжатия данных в качестве ориентира для «общего интеллекта». [2]
Различие данных
Основная статья: Сравнение данных
Сжатие данных можно рассматривать как особый случай разности данных: [3] [4] разность данных состоит из создания разности для источника и цели , с исправлением для создания цели с учетом источника, и разницы , , в то время как сжатие данных состоит из создания сжатого файла с заданной целью, а декомпрессия состоит из создания цели из только сжатого файла.Таким образом, сжатие данных можно рассматривать как разность данных с пустыми исходными данными, причем сжатый файл соответствует «отличию от ничего». Это то же самое, что рассматривать абсолютную энтропию (соответствующую сжатию данных) как частный случай относительной энтропии (соответствующей разности данных) без начальных данных.
Если кто-то хочет подчеркнуть связь, можно использовать термин разностное сжатие для обозначения разности данных.
Перспективы и неиспользованный в настоящее время потенциал
Предполагается, что общий объем информации, хранящейся на мировых запоминающих устройствах, может быть дополнительно сжат с оставшимся средним коэффициентом 4.5: 1 с существующими алгоритмами сжатия, что означает, что благодаря сжатию мир может хранить в 4,5 раза больше информации на своих существующих устройствах хранения, чем в настоящее время (по оценкам, совокупные технологические возможности мира для хранения информации составляют 1300 эксабайт аппаратных цифр в 2007 году, но когда соответствующий контент оптимально сжат, он представляет только 295 эксабайт информации Шеннона) [1] .
использует
Аудио
Сжатие звука — это форма сжатия данных , предназначенная для уменьшения требований к полосе пропускания передачи цифровых аудиопотоков и размера хранилища аудиофайлов.Алгоритмы сжатия звука реализованы в компьютерном программном обеспечении как аудиокодеки. Общие алгоритмы сжатия данных плохо работают с аудиоданными, редко уменьшая размер данных намного ниже 87% от исходного, [ требуется ссылка ] и не предназначены для использования в приложениях реального времени. Следовательно, были созданы специально оптимизированные алгоритмы аудио без потерь и с потерями. Алгоритмы с потерями обеспечивают более высокую степень сжатия и используются в обычных бытовых аудиоустройствах.
При сжатии как с потерями, так и без потерь избыточность информации снижается за счет использования таких методов, как кодирование, распознавание образов и линейное прогнозирование, чтобы уменьшить количество информации, используемой для представления несжатых данных.
Последнее перевешивает компромисс между немного сниженным качеством звука и размером передачи или хранилища для большинства практических аудиоприложений, в которых пользователи могут не ощущать потери качества воспроизведения при воспроизведении. Например, на одном компакт-диске содержится примерно один час несжатой музыки высокого качества, менее 2 часов музыки, сжатой без потерь, или 7 часов музыки, сжатой в формате MP3 со средней скоростью передачи данных.
Сжатие звука без потерь
Сжатие звука без потерь создает представление цифровых данных, которое может быть расширено до точной цифровой копии исходного аудиопотока. Это контрастирует с необратимыми изменениями при воспроизведении из таких методов сжатия с потерями, как Vorbis и MP3. Коэффициенты сжатия аналогичны коэффициентам сжатия данных без потерь (около 50–60% от исходного размера [5] ) и значительно ниже, чем при сжатии с потерями, которое обычно дает 5–20% исходного размера. [6]
Основные области применения кодирования без потерь:
- Архив
- Для архивных целей обычно желательно точно сохранить исходный материал (то есть в «наилучшем возможном качестве»).
- Монтаж
- Аудиоинженеры используют сжатие без потерь для редактирования звука, чтобы избежать потери цифрового поколения.
- Воспроизведение с высокой точностью
- Аудиофилы предпочитают форматы сжатия без потерь, чтобы избежать артефактов сжатия.
- Создание мастер-копий для массового производства аудио
- Высококачественные сжатые без потерь мастер-копии записей используются для создания версий с потерями для цифровых аудиоплееров. По мере совершенствования форматов и кодировщиков обновленные сжатые с потерями файлы могут быть сгенерированы из мастера без потерь.
- По мере того, как хранилище файлов и пропускная способность связи стали менее дорогими и более доступными, сжатие звука без потерь стало более популярным. [ необходима ссылка ]
Форматы
Shorten был ранним форматом без потерь; новые включают свободный аудиокодек без потерь (FLAC), Apple без потерь, MPEG-4 ALS, Windows Media Audio 9 без потерь (WMA без потерь), Monkey’s Audio и TTA.Полный список см. В списке кодеков без потерь.
Некоторые аудиоформаты содержат комбинацию формата с потерями и коррекции без потерь; это позволяет удалить исправление, чтобы легко получить файл с потерями. К таким форматам относятся MPEG-4 SLS (с масштабированием до без потерь), WavPack и OptimFROG DualStream.
Некоторые форматы связаны с технологией, например:
Трудности при сжатии аудиоданных без потерь
Трудно сохранить все данные в аудиопотоке и добиться существенного сжатия.Во-первых, подавляющее большинство звукозаписей очень сложны и записаны в реальном мире. Поскольку одним из ключевых методов сжатия является поиск закономерностей и повторений, более хаотичные данные, такие как аудио, не сжимаются хорошо. Точно так же фотографии сжимаются менее эффективно с помощью методов без потерь, чем более простые изображения, сгенерированные компьютером. [ необходима ссылка ] Но что интересно, даже звуки, сгенерированные компьютером, могут содержать очень сложные формы волны, которые представляют проблему для многих алгоритмов сжатия.Это связано с природой звуковых сигналов, которые обычно трудно упростить без преобразования (обязательно с потерями) в частотную информацию, которое выполняется человеческим ухом.
Вторая причина заключается в том, что значения аудиосэмплов меняются очень быстро, поэтому общие алгоритмы сжатия данных не работают для звука, а строки последовательных байтов обычно появляются не очень часто. Однако свертка с фильтром [-1 1] (то есть получение первой производной) имеет тенденцию слегка осветлить (декоррелировать, сделать плоский) спектр, тем самым позволяя традиционному сжатию без потерь в кодере выполнять свою работу; интеграция в декодере восстанавливает исходный сигнал.Такие кодеки, как FLAC, Shorten и TTA, используют линейное предсказание для оценки спектра сигнала. В кодере инверсия оценщика используется для обесцвечивания сигнала путем удаления спектральных пиков, тогда как оценщик используется для восстановления исходного сигнала в декодере.
Критерии оценки
Аудиокодеки без потерь не имеют проблем с качеством, поэтому удобство использования можно оценить на
- Скорость сжатия и декомпрессии
- Степень сжатия
- Надежность и исправление ошибок
- Поддержка продукта
Сжатие звука с потерями
Сравнение акустических спектрограмм песни в несжатом формате и различных форматах с потерями.Тот факт, что спектрограммы с потерями отличаются от несжатой, указывает на то, что они фактически содержат потери, но ничего нельзя предположить о влиянии изменений на воспринимаемое качество .
Сжатие звука с потерями используется в широком спектре приложений. В дополнение к прямым приложениям (mp3-плейеры или компьютеры) аудиопотоки с цифровым сжатием используются в большинстве DVD-видео; цифровое телевидение; потоковое мультимедиа в Интернете; спутниковое и кабельное радио; и все чаще в наземных радиопередачах.Сжатие с потерями обычно обеспечивает гораздо большее сжатие, чем сжатие без потерь (данные от 5 до 20 процентов исходного потока, а не от 50 до 60 процентов) за счет отбрасывания менее важных данных.
Инновация сжатия звука с потерями заключалась в использовании психоакустики для распознавания того, что не все данные в аудиопотоке могут восприниматься слуховой системой человека. В большинстве случаев сжатие с потерями снижает избыточность восприятия, сначала идентифицируя звуки, которые считаются несущественными для восприятия, то есть звуки, которые очень трудно услышать.Типичные примеры включают высокие частоты или звуки, которые появляются одновременно с более громкими звуками. Эти звуки кодируются с пониженной точностью или вообще не кодируются.
Из-за природы алгоритмов с потерями качество звука ухудшается, когда файл распаковывается и повторно сжимается (потеря цифрового поколения). Это делает сжатие с потерями непригодным для хранения промежуточных результатов в профессиональных аудиотехнических приложениях, таких как редактирование звука и многодорожечная запись. Однако они очень популярны среди конечных пользователей (особенно MP3), поскольку в мегабайте может храниться около минуты музыки с адекватным качеством.
Методы кодирования
Для определения того, какая информация в аудиосигнале не имеет отношения к восприятию, большинство алгоритмов сжатия с потерями используют преобразования, такие как модифицированное дискретное косинусное преобразование (MDCT), для преобразования дискретизированных сигналов временной области в область преобразования. После преобразования, обычно в частотную область, частотам компонентов могут быть назначены биты в соответствии с их слышимостью. Слышимость спектральных компонентов определяется сначала путем расчета порога маскировки, ниже которого предполагается, что звуки будут за пределами человеческого восприятия.
Порог маскировки рассчитывается с использованием абсолютного порога слышимости и принципов одновременного маскирования — явления, при котором сигнал маскируется другим сигналом, разделенным по частоте, и, в некоторых случаях, временного маскирования — когда сигнал маскируется другим сигналом. разделены временем. Контуры равной громкости также могут использоваться для взвешивания важности восприятия различных компонентов. Модели сочетания человеческого уха и мозга, включающие такие эффекты, часто называют психоакустическими моделями.
Другие типы компрессоров с потерями, такие как кодирование с линейным предсказанием (LPC), используемое с речью, — это кодеры на основе источника . Эти кодеры используют модель генератора звука (например, речевой тракт человека с LPC) для обесцвечивания аудиосигнала (т.е. сглаживания его спектра) перед квантованием. LPC можно также рассматривать как базовую технику перцептивного кодирования; Реконструкция аудиосигнала с использованием линейного предсказателя преобразует шум квантования кодера в спектр целевого сигнала, частично маскируя его.
Удобство использования
Возможность использования аудиокодеков с потерями определяется:
- Воспринимаемое качество звука
- Коэффициент сжатия
- Скорость сжатия и декомпрессии
- Собственная задержка алгоритма (критически важна для потоковых приложений в реальном времени; см. Ниже)
- Поддержка продукта
Форматы с потерями часто используются для распространения потокового аудио или интерактивных приложений (таких как кодирование речи для цифровой передачи в сетях сотовой связи).В таких приложениях данные должны распаковываться по мере потока данных, а не после того, как весь поток данных был передан. Не все аудиокодеки могут использоваться для потоковых приложений, и для таких приложений обычно выбирается кодек, предназначенный для эффективной потоковой передачи данных.
Задержка возникает из-за методов, используемых для кодирования и декодирования данных. Некоторые кодеки будут анализировать более длинный сегмент данных для оптимизации эффективности, а затем кодировать его таким образом, чтобы для декодирования требовался более крупный сегмент данных за один раз.(Часто кодеки создают сегменты, называемые «кадром», для создания дискретных сегментов данных для кодирования и декодирования.) Внутренняя задержка алгоритма кодирования может быть критической; например, при двусторонней передаче данных, такой как телефонный разговор, значительные задержки могут серьезно ухудшить воспринимаемое качество.
В отличие от скорости сжатия, которая пропорциональна количеству операций, требуемых алгоритмом, здесь под задержкой понимается количество выборок, которые должны быть проанализированы перед обработкой блока аудио.В минимальном случае задержка составляет 0 нулевых отсчетов (например, если кодер / декодер просто уменьшает количество битов, используемых для квантования сигнала). Алгоритмы временной области, такие как LPC, также часто имеют низкие задержки, отсюда их популярность в кодировании речи для телефонии. Однако в таких алгоритмах, как MP3, необходимо проанализировать большое количество выборок, чтобы реализовать психоакустическую модель в частотной области, а задержка составляет порядка 23 мс (46 мс для двусторонней связи).
Кодировка речи
Кодирование речи — важная категория сжатия аудиоданных.Модели восприятия, используемые для оценки того, что может слышать человеческое ухо, обычно несколько отличаются от моделей, используемых для музыки. Диапазон частот, необходимых для передачи звуков человеческого голоса, обычно намного уже, чем диапазон частот, необходимый для музыки, и звук обычно менее сложен. В результате речь может быть кодирована с высоким качеством, используя относительно низкие скорости передачи данных.
Как правило, это достигается комбинацией двух подходов:
- Кодирует только звуки, которые может издать один человеческий голос.
- Отбрасывание большего количества данных в сигнале — сохранение ровно столько, чтобы восстановить «понятный» голос, а не весь частотный диапазон человеческого слуха.
Возможно, самыми ранними алгоритмами, использовавшимися при кодировании речи (и сжатии аудиоданных в целом), были алгоритм А-закона и алгоритм µ-закона.
История
Solidyne 922: первая в мире коммерческая карта сжатия битов аудио для ПК, 1990 г.
Сборник литературы по большому количеству систем кодирования звука был опубликован в журнале IEEE Journal on Selected Areas in Communications (JSAC) в феврале 1988 г.Несмотря на то, что были некоторые документы до того времени, эта коллекция документировала все разнообразие законченных, работающих аудиокодеров, почти все из которых использовали методы восприятия (то есть маскирования) и своего рода частотный анализ и внутреннее бесшумное кодирование. [7] В некоторых из этих статей отмечена сложность получения хорошего, чистого цифрового звука для исследовательских целей. Большинство, если не все, авторы издания JSAC также были активны в комитете MPEG-1 Audio.
Первая в мире система сжатия звука для автоматизации коммерческого вещания была разработана Оскаром Бонелло, профессором инженерии в Университете Буэнос-Айреса. [8] В 1983 году, используя психоакустический принцип маскировки критических полос, впервые опубликованный в 1967 году, [9] он начал разработку практического приложения на основе недавно разработанного компьютера IBM PC, и была запущена система автоматизации вещания. в 1987 году под названием Audicom. Спустя 20 лет почти все радиостанции мира использовали аналогичную технологию, произведенную рядом компаний.
Видео
Сжатие видео относится к уменьшению объема данных, используемых для представления цифровых видеоизображений, и представляет собой комбинацию пространственного сжатия изображения и временной компенсации движения.Сжатие видео является примером концепции кодирования источника в теории информации. В этой статье рассматриваются его приложения: сжатое видео может эффективно уменьшить полосу пропускания, необходимую для передачи видео через наземное вещание, через кабельное телевидение или через службы спутникового телевидения.
Качество видео
В большинстве случаев сжатие видеосигнала происходит с потерями: оно работает исходя из предположения, что большая часть данных, представленных до сжатия, не является необходимой для достижения хорошего качества восприятия. Например, DVD используют стандарт кодирования видео под названием MPEG-2, который может сжимать видеоданные в 15–30 раз, сохраняя при этом качество изображения, которое обычно считается высоким для видео стандартной четкости.Сжатие видео — это компромисс между дисковым пространством, качеством видео и стоимостью оборудования, необходимого для распаковки видео в разумные сроки. Однако, если видео чрезмерно сжато с потерями, могут появиться видимые (а иногда и отвлекающие) артефакты.
Сжатие видео обычно работает с квадратными группами соседних пикселей, часто называемыми макроблоками. Эти группы пикселей или блоки пикселей сравниваются от одного кадра к другому, и кодек сжатия видео (схема кодирования / декодирования) отправляет только разностей в этих блоках.Это очень хорошо работает, если в видео нет движения. Например, неподвижный текстовый кадр может повторяться с очень небольшим количеством передаваемых данных. В областях видео с большим количеством движения больше пикселей изменяется от одного кадра к другому. Когда изменяется больше пикселей, схема сжатия видео должна отправлять больше данных, чтобы не отставать от большего количества изменяющихся пикселей. Если видеоконтент включает взрыв, пламя, стаю тысяч птиц или любое другое изображение с большим количеством высокочастотных деталей, качество снизится или переменный битрейт должен быть увеличен, чтобы отобразить эту добавленную информацию с помощью такой же уровень детализации.
Поставщик программ может контролировать степень сжатия видео, применяемого к их программам видео, перед отправкой в их систему распространения. Для DVD, Blu-ray и HD DVD в процессе мастеринга применяется сжатие видео, хотя Blu-ray и HD DVD имеют достаточную емкость диска, поэтому в большинстве случаев сжатие, применяемое в этих форматах, является легким по сравнению с такими примерами, как большинство потокового видео. в Интернете или на мобильный телефон. Программное обеспечение, используемое для хранения видео на жестких дисках или различных форматах оптических дисков, часто имеет более низкое качество изображения.Видеокодеки с высокой скоростью передачи данных с небольшим сжатием или без него существуют для пост-обработки видео, но создают очень большие файлы и поэтому почти никогда не используются для распространения готовых видеороликов. Если чрезмерное сжатие видео с потерями ухудшает качество изображения, восстановить исходное качество изображения невозможно.
Теория
Видео — это в основном трехмерный массив цветных пикселей. Два измерения служат пространственными (горизонтальным и вертикальным) направлениями движущихся изображений, а одно измерение представляет временную область.Фрейм данных — это набор всех пикселей, которые соответствуют одному моменту времени. По сути, кадр такой же, как и неподвижное изображение.
Видеоданные содержат пространственную и временную избыточность. Таким образом, сходства можно кодировать, просто регистрируя различия внутри кадра (пространственного) и / или между кадрами (временного). Пространственное кодирование выполняется с использованием преимущества того факта, что человеческий глаз не может различать небольшие различия в цвете так же легко, как он может воспринимать изменения яркости, поэтому очень похожие области цвета могут быть «усреднены» таким же образом, как и изображения в формате jpeg. [10] При временном сжатии кодируются только изменения от одного кадра к другому, так как часто большое количество пикселей будет одинаковым в серии кадров.
Сжатие без потерь
Некоторые формы сжатия данных без потерь. Это означает, что при распаковке данных результат побитово идеально совпадает с оригиналом. Хотя сжатие видео без потерь возможно, оно используется редко, поскольку сжатие с потерями приводит к гораздо более высоким коэффициентам сжатия при приемлемом уровне качества.
Сравнение внутрикадрового и межкадрового сжатия
Одним из самых эффективных методов сжатия видео является межкадровое сжатие. Межкадровое сжатие использует один или несколько более ранних или более поздних кадров в последовательности для сжатия текущего кадра, тогда как внутрикадровое сжатие использует только текущий кадр, что фактически является сжатием изображения.
Наиболее часто используемый метод заключается в сравнении каждого кадра видео с предыдущим. Если кадр содержит области, в которых ничего не перемещалось, система просто выдает короткую команду, которая побитно копирует эту часть предыдущего кадра в следующий.Если части кадра перемещаются простым способом, компрессор выдает команду (немного более длинную), которая сообщает декомпрессору сдвинуть, повернуть, осветлить или затемнить копию: более длинная команда, но все же намного короче, чем внутрикадровое сжатие. Межкадровое сжатие хорошо работает для программ, которые просто воспроизводятся зрителем, но может вызвать проблемы, если видеоряд необходимо отредактировать.
Поскольку при межкадровом сжатии данные копируются из одного кадра в другой, если исходный кадр просто вырезан (или потерян при передаче), следующие кадры не могут быть восстановлены должным образом.Некоторые видеоформаты, такие как DV, сжимают каждый кадр независимо, используя внутрикадровое сжатие. Нарезать внутрикадровое сжатое видео почти так же просто, как и редактировать несжатое видео: найти начало и конец каждого кадра, просто побитно копировать каждый кадр, который нужно сохранить, и отбрасывать кадры, которые он не делал. не хочу. Еще одно различие между внутрикадровым и межкадровым сжатием состоит в том, что в внутрикадровых системах каждый кадр использует одинаковый объем данных. В большинстве межкадровых систем определенным кадрам (например, «I-кадрам» в MPEG-2) не разрешается копировать данные из других кадров, и поэтому требуется гораздо больше данных, чем для других кадров поблизости.
Можно создать компьютерный видеоредактор, который выявляет проблемы, возникающие, когда I-кадры редактируются, в то время как другие кадры нуждаются в них. Это позволило использовать для редактирования новые форматы, такие как HDV. Однако этот процесс требует гораздо большей вычислительной мощности, чем редактирование внутрикадрового сжатого видео с тем же качеством изображения.
Действующие формы
Сегодня почти во всех широко используемых методах сжатия видео (например, в стандартах, утвержденных ITU-T или ISO) применяется дискретное косинусное преобразование (DCT) для уменьшения пространственной избыточности.Другие методы, такие как фрактальное сжатие, поиск соответствия и использование дискретного вейвлет-преобразования (DWT), были предметом некоторых исследований, но, как правило, не используются в практических продуктах (за исключением использования вейвлет-кодирования в качестве кодеров неподвижных изображений. без компенсации движения). Интерес к фрактальному сжатию, кажется, ослабевает из-за недавнего теоретического анализа, показывающего сравнительную неэффективность таких методов. [ необходима ссылка ]
Хронология
Следующая таблица представляет собой частичную историю международных стандартов сжатия видео.
| Год | Стандартный | Издатель | Популярные реализации |
|---|---|---|---|
| 1984 | H.120 | ITU-T | |
| 1990 | H.261 | ITU-T | Видеоконференцсвязь, видеотелефония |
| 1993 | MPEG-1, часть 2 | ISO, IEC | Видео-CD |
| 1995 | H.262 / MPEG-2, часть 2 | ISO, IEC, ITU-T | DVD-видео, Blu-ray, цифровое видеовещание, SVCD |
| 1996 | H. a b «Мировой технологический потенциал для хранения, передачи и вычисления информации», в частности, поддержка онлайн-материалов, Мартин Хилберт и Присцила Лопес (2011), Science (журнал) , 332 (6025), 60-65; свободный доступ к статье здесь: martinhilbert. http://www.faqs.org/faqs/jpeg-faq/part1/Внешние ссылкиСтраница не найдена | MITПерейти к содержанию ↓
Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали! Что вы ищете? Увидеть больше результатов Предложения или отзывы? Методы сжатия данныхРаскрытие информации рекламодателя
. |
 3. Пример кодирования Хаффмана
3. Пример кодирования Хаффмана Результаты кодирования по методу Хаффмана
Результаты кодирования по методу Хаффмана ...
...