Пример больше меньше или равно: Обыкновенные дроби — Определение, Примеры, Действия, Доли, Числитель и Знаменатель
Общие сведения о неравенствах
Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.
Предварительные навыки
Определения и свойства
Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, <, ≥, ≤ или ≠.
Пример: 5 > 3
Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.
Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:
Если 5 > 3, то 3 < 5. То есть левую и правую часть неравенства можно поменять местами, изменив знак неравенства на противоположный. В ситуации с весами: большой арбуз можно положить на правую чашу, а маленький арбуз на левую. Тогда правая чаша перевесит левую, и экран покажет знак <
Если в неравенстве 5 > 3, не трогая левую и правую часть, поменять знак на <, то получится неравенство 5 < 3. Это неравенство не является верным, поскольку число 3 не может быть больше числа 5.
Это неравенство не является верным, поскольку число 3 не может быть больше числа 5.
Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.
Рассмотрим некоторые важные свойства для неравенства 5 > 3.
В будущем эти свойства будут работать и для других неравенств.
Свойство 1.
Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.
Например, прибавим к обеим частям неравенства число 4. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2
Видим, что левая часть по-прежнему больше правой.
Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.
Знак неравенства при этом не изменится.
Например, перенесём в неравенстве 5 > 3, член 5 из левой части в правую часть, изменив знак этого члена. После переноса члена 5 в правую часть, в левой части ничего не останется, поэтому запишем там 0
0 > 3 − 5
0 > −2
Видим, что левая часть по-прежнему больше правой.
Свойство 2.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2
Видим, что левая часть по-прежнему больше правой.
Свойство 3.
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь отрицательное число, скажем на число −2. Тогда получим:
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.
Например, чтобы ответить на вопрос является ли верным неравенство 7 > 3, нужно проверить выполняется ли условие «больше ли 7, чем 3». Мы знаем, что число 7 больше, чем число 3. То есть условие выполнено, а значит и неравенство 7 > 3 верно.
Неравенство 8 < 6 не является верным, поскольку не выполняется условие «8 меньше, чем 6».
Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:
Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.
Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.
Составим разность из членов 7 и 3. Тогда получим 7 − 3 = 4. Согласно правилу, число 7 будет больше числа 3, если разность 7 − 3 окажется положительной. У нас она равна 4, то есть разность положительна. А значит число 7 больше числа 3.
Проверим с помощью разности верно ли неравенство 3 < 4. Составим разность, получим 3 − 4 = −1. Согласно правилу, число 3 будет меньше числа 4, если разность 3 − 4 окажется отрицательной. У нас она равна −1, то есть разность отрицательна. А значит число 3 меньше числа 4.
Согласно правилу, число 3 будет меньше числа 4, если разность 3 − 4 окажется отрицательной. У нас она равна −1, то есть разность отрицательна. А значит число 3 меньше числа 4.
Проверим верно ли неравенство 5 > 8. Составим разность, получим 5 − 8 = −3. Согласно правилу, число 5 будет больше числа 8, если разность 5 − 8 окажется положительной. У нас разность равна −3, то есть она не является положительной. А значит число 5 не больше числа 3. Иными словами, неравенство 5 > 8 не является верным.
Строгие и нестрогие неравенства
Неравенства, содержащие знаки >, < называют строгими. А неравенства, содержащие знаки ≥, ≤ называют нестрогими.
Примеры строгих неравенства мы рассматривали ранее. Таковыми являются неравенства 5 > 3, 7 < 9.
Нестрогим, например, является неравенство 2 ≤ 5. Данное неравенство читают следующим образом: «2 меньше или равно 5».
Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:
Полная запись этого неравенства выглядит следующим образом:
2 < 5 или 2 = 5
Тогда становится очевидным, что неравенство 2 ≤ 5 состоит из двух условий: «два меньше пять» и «два равно пять».
Нестрогое неравенство верно в том случае, если выполняется хотя бы одно из его условий. В нашем примере верным является условие «2 меньше 5». Значит и само неравенство 2 ≤ 5 верно.
Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.
Пример 3. Неравенство 5 ≤ 2 не является верным, поскольку не выполняется ни одно из его условий: ни 5 < 2 ни 5 = 2.
Двойное неравенство
Число 3 больше, чем число 2 и меньше, чем число 4. В виде неравенства это высказывание можно записать так: 2 < 3 < 4. Такое неравенство называют двойным.
Двойное неравенство может содержать знаки нестрогих неравенств. К примеру, если число 5 больше или равно, чем число 2, и меньше или равно, чем число 7, то можно записать, что 2 ≤ 5 ≤ 7
Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.
Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.
Сначала записываем 6
Слева записываем, что это число больше, чем число 4
Справа записываем, что число 6 меньше, чем число 9
Неравенство с переменной
Неравенство, как и равенство может содержать переменную.
Например, неравенство x > 2 содержит переменную x. Обычно такое неравенство нужно решить, то есть выяснить при каких значениях x данное неравенство становится верным.
Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.
Значение переменной, при котором неравенство становится верным, называется решением неравенства.
Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.
Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:
3 > 2
4 > 2
5 > 2
Число 2, располагающееся в правой части неравенства x > 2, будем называть границей данного неравенства. В зависимости от знака неравенства, граница может принадлежать множеству решений неравенства либо не принадлежать ему.
В нашем примере граница неравенства не принадлежит множеству решений, поскольку при подстановке числа 2 в неравенство x > 2 получается не верное неравенство 2 > 2. Число 2 не может быть больше самого себя, поскольку оно равно самому себе (2 = 2).
Неравенство x > 2 является строгим. Его можно прочитать так: «x строго больше 2″. То есть все значения, принимаемые переменной x должны быть строго больше 2. В противном случае, неравенство верным не будет.
Если бы нам было дано нестрогое неравенство x ≥ 2, то решениями данного неравенства были бы все числа, которые больше 2, в том числе и само число 2. В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2. Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2, поэтому и само неравенство 2 ≥ 2 верно.
В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2. Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2, поэтому и само неравенство 2 ≥ 2 верно.
Как решать неравенства
Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.
Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.
Решая уравнения мы выполняли тождественные преобразования до тех пор, пока в левой части уравнения не оставалась переменная, а в правой части значение этой переменной (например: x = 2, x = 5). Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a, где a значение переменной x. В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a, где a значение переменной x. В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.
Пример 1. Решить неравенство 2x > 6
Итак, нужно найти такие значения x, при подстановке которых в 2x > 6 получится верное неравенство.
Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.
В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.
Итак, разделим обе части неравенства на 2.
В левой части осталась переменная x, а правая часть стала равна 3. Получилось равносильное неравенство x > 3. На этом решение завершается, поскольку в левой части осталась переменная, а в правой части граница неравенства.
Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.
4 > 3
5 > 3
6 > 3
7 > 3
Отметим, что неравенство x > 3 является строгим. «Переменная x строго больше трёх».
А поскольку неравенство x > 3 равносильно исходному неравенству 2x > 6, то их решения будут совпадать. Иначе говоря, значения, которые подходят неравенству x > 3, будут подходить и неравенству 2x > 6. Покажем это.
Возьмём, например, число 5 и подставим его сначала в полученное нами равносильное неравенство x > 3, а потом в исходное 2x > 6.
Видим, что в обоих случаях получается верное неравенство.
После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:
В этом выражении говорится, что значения, принимаемые переменной x, принадлежат числовому промежутку от трёх до плюс бесконечности.
Иначе говоря, все числа, начиная от трёх до плюс бесконечности являются решениями неравенства x > 3. Знак ∞ в математике означает бесконечность.
Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.
Числовые промежутки
Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.
Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.
Границы могут принадлежать числовому промежутку либо не принадлежать ему.
Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.
Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.
На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.
Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:
В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.
На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.
Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.
Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.
На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:
На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.
На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.
С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:
x ∈ [ 2 ; 8 ]
То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
Обратим внимание на то, что ответ записан с помощью квадратных скобок, поскольку границы неравенства 2 ≤ x ≤ 8, а именно числа 2 и 8 принадлежат множеству решений этого неравенства.
Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:
Здесь границы числового промежутка 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8.
В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.
Открытыми их называют по той причине, что числовой промежуток остаётся открытым из-за того, что его границы не принадлежат этому числовому промежутку. Пустой кружок на координатной прямой математики называют выколотой точкой. Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
Пустой кружок на координатной прямой математики называют выколотой точкой. Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.
Существуют разновидности числовых промежутков. Рассмотрим каждый из них.
Числовой луч
Числовым лучом называют числовой промежуток, который задаётся неравенством x ≥ a, где a — граница данного неравенства, x — решение неравенства.
Пусть a = 3. Тогда неравенство x ≥ a примет вид x ≥ 3. Решениями данного неравенства являются все числа, которые больше 3, включая само число 3.
Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Здесь точка 3 соответствует границе неравенства x ≥ 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≥ 3.
Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.
На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:
[ a ; +∞ )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.
Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.
Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3
x ∈ [ 3 ; +∞ )
В этом выражении говорится, что переменная x, входящая в неравенство x ≥ 3, принимает все значения от 3 до плюс бесконечности.
Иначе говоря, все числа от 3 до плюс бесконечности, являются решениями неравенства x ≥ 3. Граница 3 принадлежит множеству решений, поскольку неравенство x ≥ 3 является нестрогим.
Закрытым числовым лучом также называют числовой промежуток, который задаётся неравенством x ≤ a. Решениями неравенства x ≤ a являются все числа, которые меньше a, включая само число a.
К примеру, если a = 2, то неравенство примет вид x ≤ 2. На координатной прямой граница 2 будет изображаться закрашенным кружком, а вся область, находящаяся слева, будет выделена штрихами.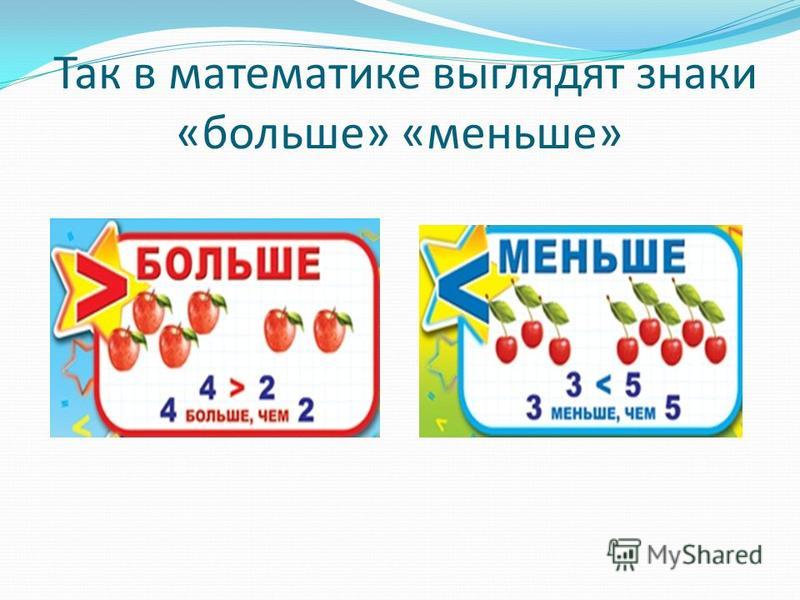 В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
Здесь точка 2 соответствует границе неравенства x ≤ 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≤ 2.
Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.
Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:
x ∈ ( −∞ ; 2 ]
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.
Открытый числовой луч
Открытым числовым лучом называют числовой промежуток, который задаётся неравенством x > a, где a — граница данного неравенства, x — решение неравенства.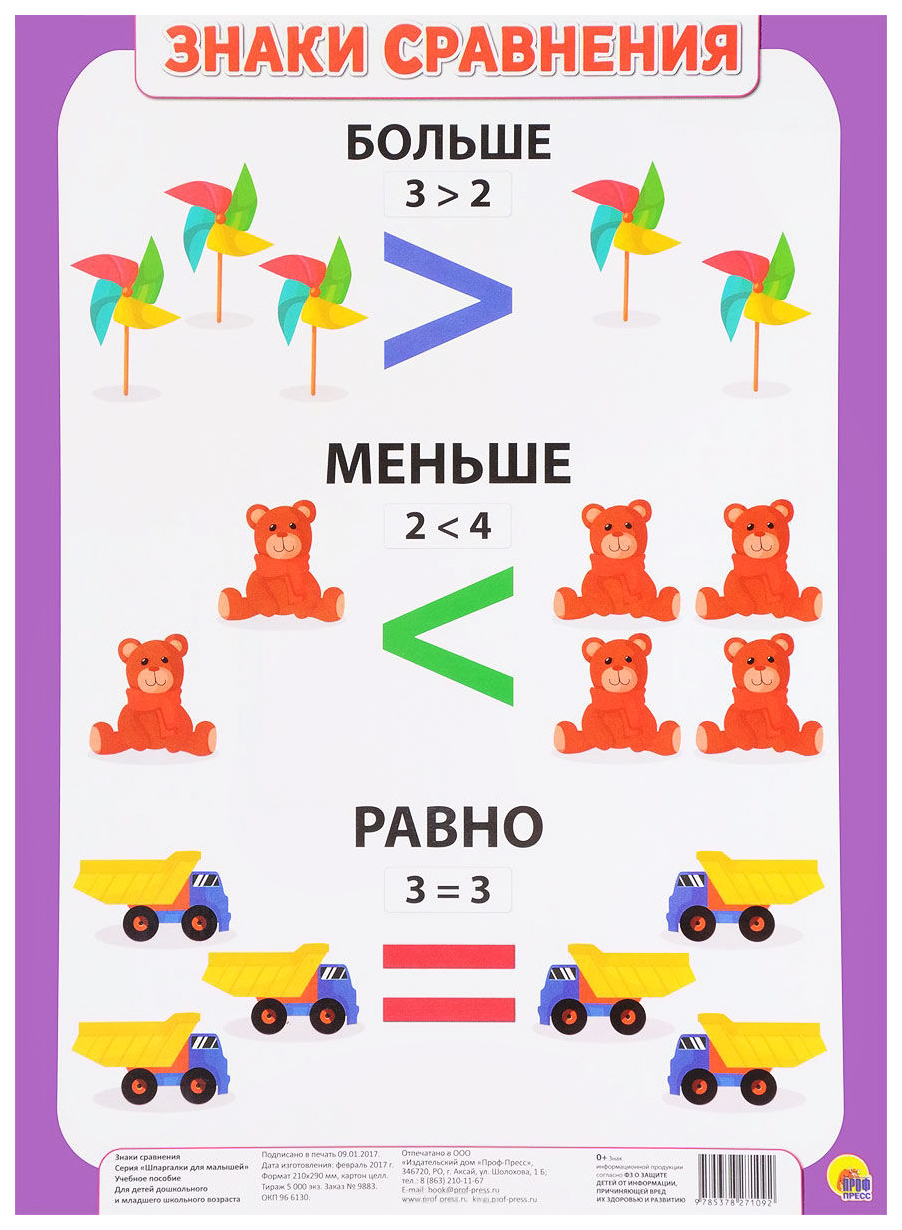
Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.
Пусть a = 3. Тогда неравенство примет вид x > 3. Решениями данного неравенства являются все числа, которые больше 3, за исключением числа 3
На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:
Здесь точка 3 соответствует границе неравенства x > 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x > 3. Точка 3, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x > 3 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x > a, обозначается следующим образом:
( a ; +∞ )
Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.
Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:
x ∈ ( 3 ; +∞ )
В этом выражении говорится, что все числа от 3 до плюс бесконечности, являются решениями неравенства x > 3. Граница 3 не принадлежит множеству решений, поскольку неравенство x > 3 является строгим.
Открытым числовым лучом также называют числовой промежуток, который задаётся неравенством x < a, где a — граница данного неравенства, x — решение неравенства. Решениями неравенства x < a являются все числа, которые меньше a, исключая число a.
К примеру, если a = 2, то неравенство примет вид x < 2. На координатной прямой граница 2 будет изображаться пустым кружком, а вся область, находящаяся слева, будет выделена штрихами:
Здесь точка 2 соответствует границе неравенства x < 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x < 2.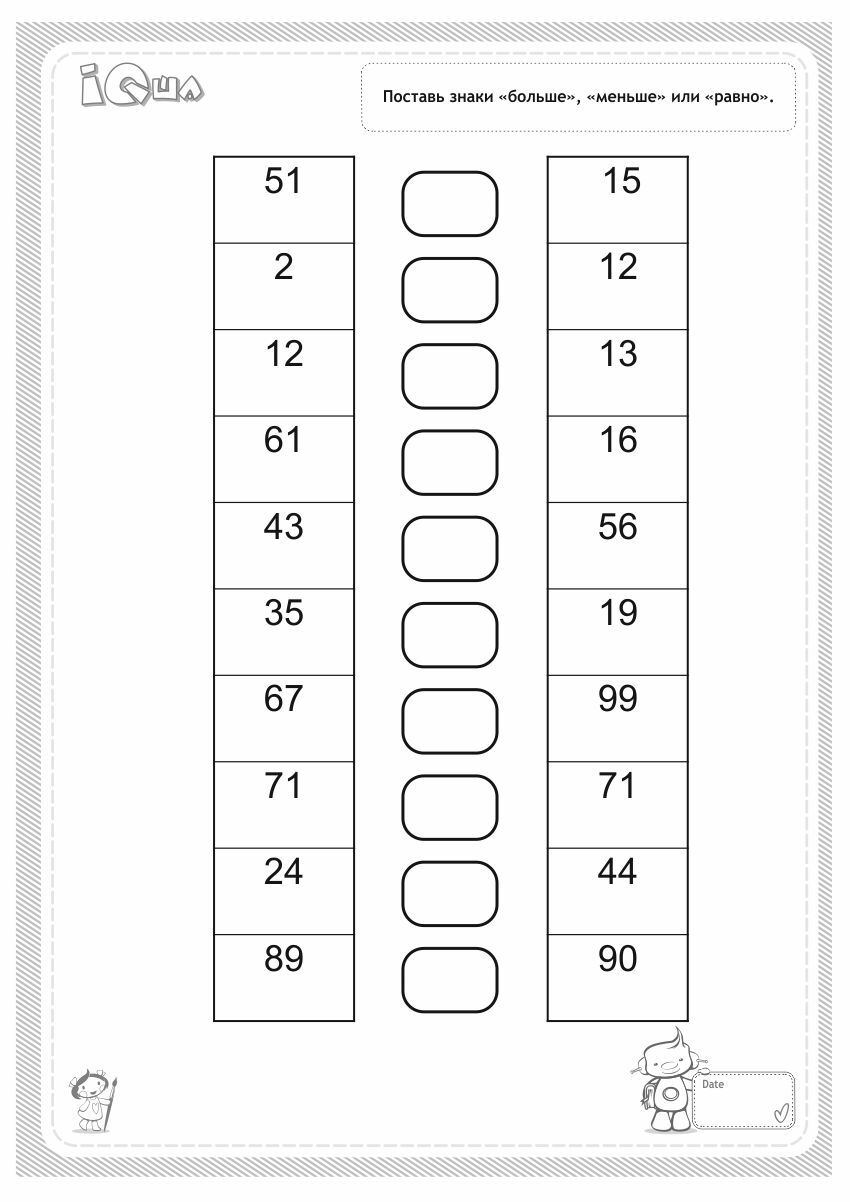 Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x < 2 не принадлежит множеству его решений.
Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x < 2 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x < a, обозначается следующим образом:
( −∞ ; a )
Запишем ответ к неравенству x < 2 с помощью обозначения открытого числового луча:
x ∈ ( −∞ ; 2 )
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x < 2. Граница 2 не принадлежит множеству решений, поскольку неравенство x < 2 является строгим.
Отрезок
Отрезком называют числовой промежуток, который задаётся двойным неравенством a ≤ x ≤ b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x ≤ b примет вид 2 ≤ x ≤ 8. Решениями неравенства 2 ≤ x ≤ 8 являются все числа, которые больше 2 и меньше 8. При этом границы неравенства 2 и 8 принадлежат множеству его решений, поскольку неравенство 2 ≤ x ≤ 8 является нестрогим.
Решениями неравенства 2 ≤ x ≤ 8 являются все числа, которые больше 2 и меньше 8. При этом границы неравенства 2 и 8 принадлежат множеству его решений, поскольку неравенство 2 ≤ x ≤ 8 является нестрогим.
Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8. Точки 2 и 8, являющиеся границами отрезка, изображены в виде закрашенных кружков, поскольку границы неравенства 2 ≤ x ≤ 8 принадлежат множеству его решений.
На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:
[ a ; b ]
Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему.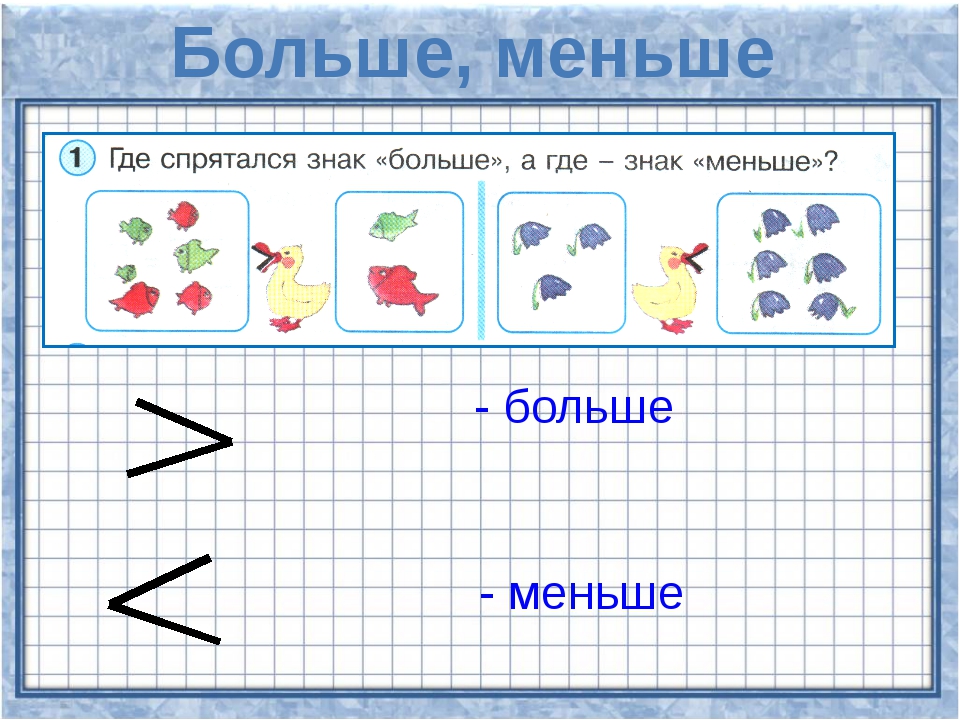 Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8 включительно, являются решениями неравенства 2 ≤ x ≤ 8.
Интервал
Интервалом называют числовой промежуток, который задаётся двойным неравенством a < x < b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a < x < b примет вид 2 < x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая числа 2 и 8.
Изобразим интервал на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x < 8. Точки 2 и 8, являющиеся границами интервала, изображены в виде пустых кружков, поскольку границы неравенства 2 < x < 8 не принадлежат множеству его решений.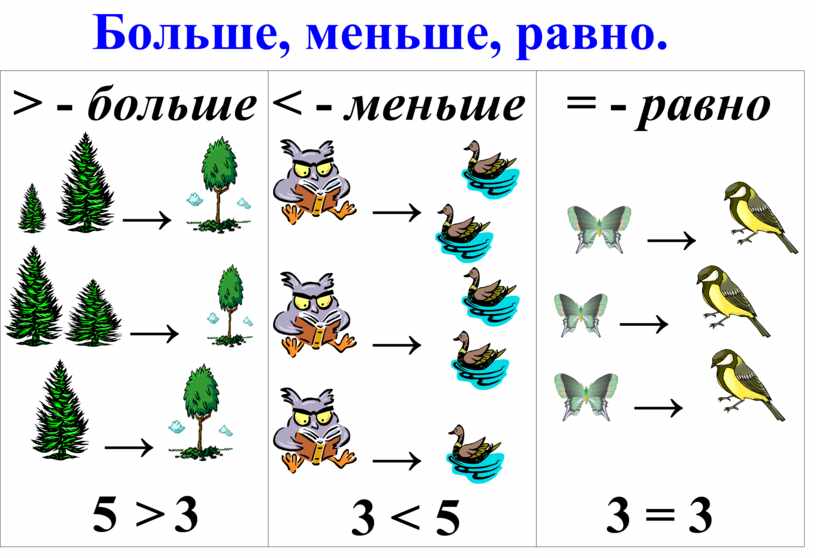
На письме интервал, заданный неравенством a < x < b, обозначается следующим образом:
( a ; b )
Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 < x < 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, исключая числа 2 и 8, являются решениями неравенства 2 < x < 8.
Полуинтервал
Полуинтервалом называют числовой промежуток, который задаётся неравенством a ≤ x < b, где a и b — границы данного неравенства, x — решение неравенства.
Полуинтервалом также называют числовой промежуток, который задаётся неравенством a < x ≤ b.
Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.
В ситуации с полуинтервалом a ≤ x < b ему (полуинтервалу) принадлежит левая граница.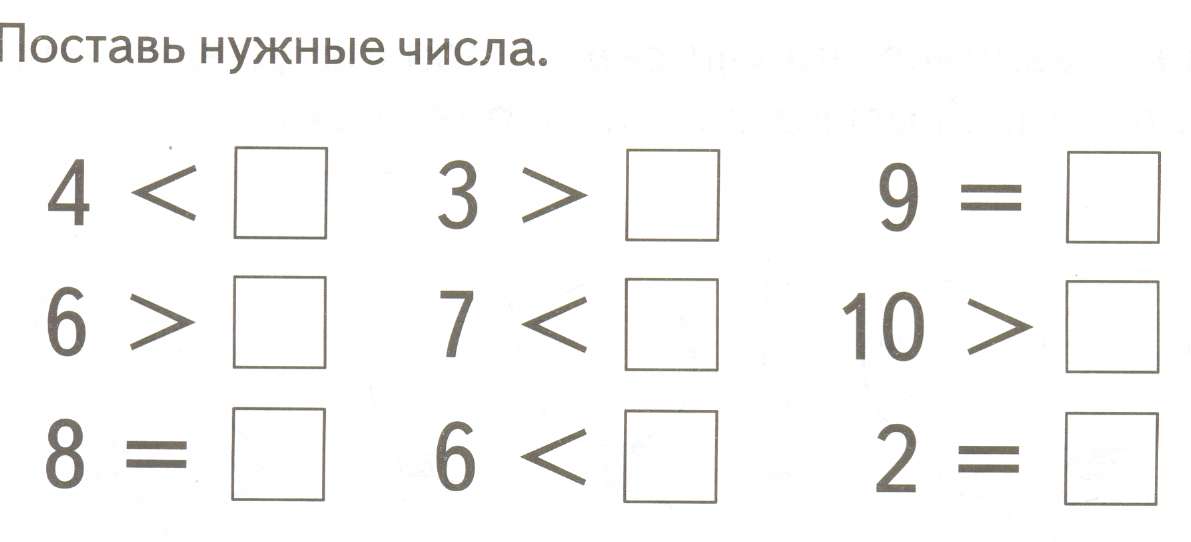
А в ситуации с полуинтервалом a < x ≤ b ему принадлежит правая граница.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x < b примет вид 2 ≤ x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, включая число 2, но исключая число 8.
Изобразим полуинтервал 2 ≤ x < 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x < 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x < 8 принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x < 8 не принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a ≤ x < b, обозначается следующим образом:
[ a ; b )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x < 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, включая число 2, но исключая число 8, являются решениями неравенства 2 ≤ x < 8.
Аналогично на координатной прямой можно изобразить полуинтервал, заданный неравенством a < x ≤ b. Пусть a = 2, b = 8. Тогда неравенство a < x ≤ b примет вид 2 < x ≤ 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая число 2, но включая число 8.
Изобразим полуинтервал 2 < x ≤ 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x ≤ 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 < x ≤ 8 не принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 < x ≤ 8 принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a < x ≤ b, обозначается так: ( a ; b ]. Запишем ответ к неравенству 2 < x ≤ 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8, исключая число 2, но включая число 8, являются решениями неравенства 2 < x ≤ 8.
Изображение числовых промежутков на координатной прямой
Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок).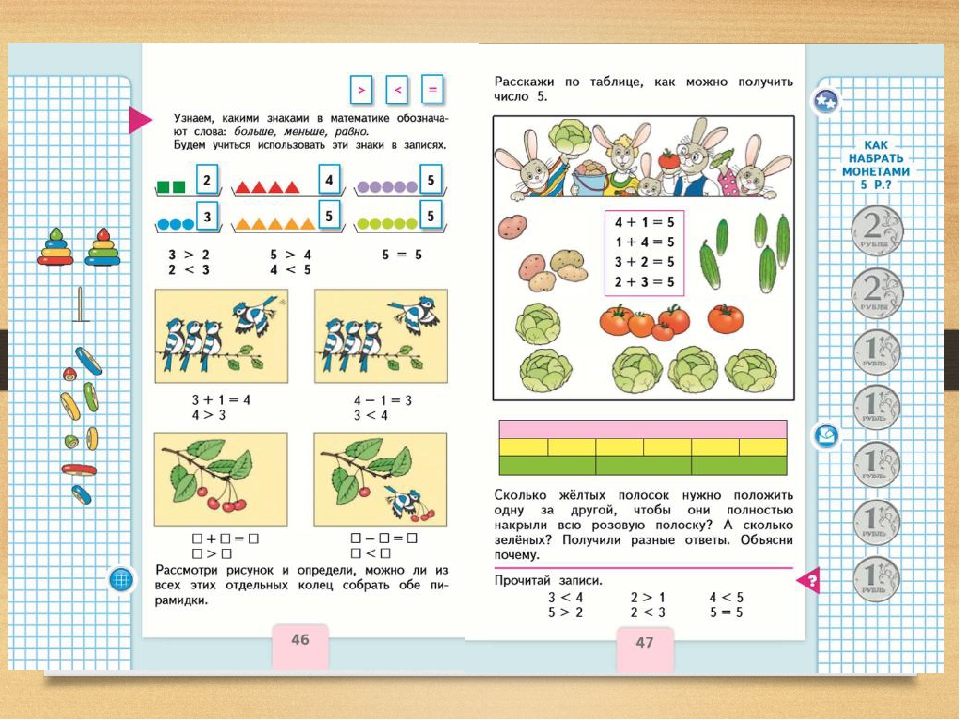 В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5
Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:
Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.
Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.
Символ +∞ указывает, что нас интересуют все числа, которые больше 5.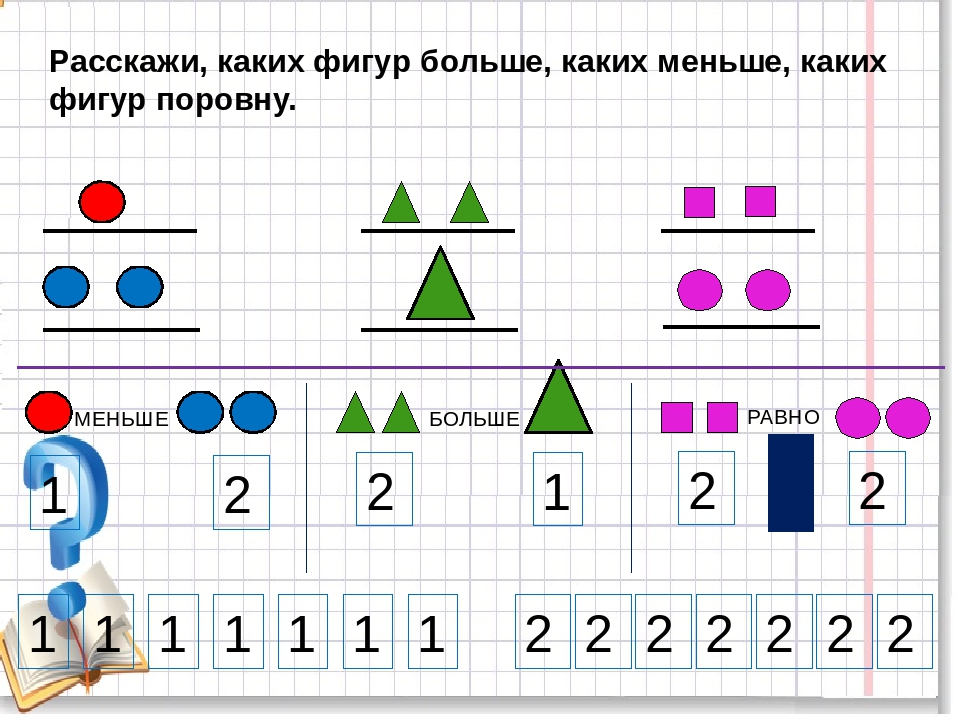 Соответственно, вся область справа от границы 5 выделяется штрихами:
Соответственно, вся область справа от границы 5 выделяется штрихами:
Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.
Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:
Пример 4. Изобразить числовой промежуток, заданный неравенством −5 < x < 1
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.
Неравенством вида a < x < b, задаётся интервал. В данном случае переменная a равна −5, а переменная b равна единице. Неравенство −5 < x < 1 строгое, поэтому границы −5 и 1 будут изображаться в виде пустых кружка. Нас интересуют все значения x, которые больше −5, но меньше единицы, поэтому вся область между точками −5 и 1 будет выделена штрихами:
Пример 5. Изобразить на координатной прямой числовые промежутки [-1; 2] и [2; 5]
Изобразить на координатной прямой числовые промежутки [-1; 2] и [2; 5]
В этот раз изобразим на координатной прямой сразу два промежутка.
Квадратными скобками с обеих сторон обозначаются отрезки. Границы отрезка принадлежат ему, поэтому границы отрезков [-1; 2] и [2; 5] будут изображаться на координатной прямой в виде закрашенных кружков. Вся область между ними будет выделена штрихами.
Чтобы хорошо увидеть промежутки [−1; 2] и [2; 5], первый можно изобразить на верхней области, а второй на нижней. Так и поступим:
Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]
Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.
В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.
А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.
Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:
Примеры решения неравенств
Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax < b), будем называть линейным неравенством с одной переменной.
В линейном неравенстве ax > b, x — это переменная, значения которой нужно найти, а — коэффициент этой переменной, b — граница неравенства, которая в зависимости от знака неравенства может принадлежать множеству его решений либо не принадлежать ему.
Например, неравенство 2x > 4 является неравенством вида ax > b. В нём роль переменной a играет число 2, роль переменной b (границы неравенства) играет число 4.
Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2
Получившееся неравенство x > 2 также является неравенством вида ax > b, то есть линейным неравенством с одной переменной. В этом неравенстве роль переменной a играет единица. Ранее мы говорили, что коэффициент 1 не записывают. Роль переменной b играет число 2.
Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b
Пример 1. Решить неравенство x − 7 < 0
Прибавим к обеим частям неравенства число 7
x − 7 + 7 < 0 + 7
В левой части останется x, а правая часть станет равна 7
x < 7
Путём элементарных преобразований мы привели неравенство x − 7 < 0 к равносильному неравенству x < 7. Решениями неравенства x < 7 являются все числа, которые меньше 7. Граница 7 не принадлежит множеству решений, поскольку неравенство строгое.
Решениями неравенства x < 7 являются все числа, которые меньше 7. Граница 7 не принадлежит множеству решений, поскольку неравенство строгое.
Когда неравенство приведено к виду x < a (или x > a), его можно считать уже решённым. Наше неравенство x − 7 < 0 тоже приведено к такому виду, а именно к виду x < 7. Но в большинстве школ требуют, чтобы ответ был записан с помощью числового промежутка и проиллюстрирован на координатной прямой.
Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x < a и обозначается как ( −∞ ; a)
x ∈ ( −∞ ; 7 )
На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:
Для проверки возьмём любое число из промежутка ( −∞ ; 7 ) и подставим его в неравенство x < 7 вместо переменной x. Возьмём, например, число 2
Возьмём, например, число 2
2 < 7
Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4
4 < 7
Получилось верное числовое неравенство. Значит решение верное.
А поскольку неравенство x < 7 равносильно исходному неравенству x − 7 < 0, то решения неравенства x < 7 будут совпадать с решениями неравенства x − 7 < 0. Подставим те же тестовые значения 2 и 4 в неравенство x − 7 < 0
2 − 7 < 0
−5 < 0 — Верное неравенство
4 − 7 < 0
−3 < 0 Верное неравенство
Пример 2. Решить неравенство −4x < −16
Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Мы привели неравенство −4x < −16 к равносильному неравенству x > 4.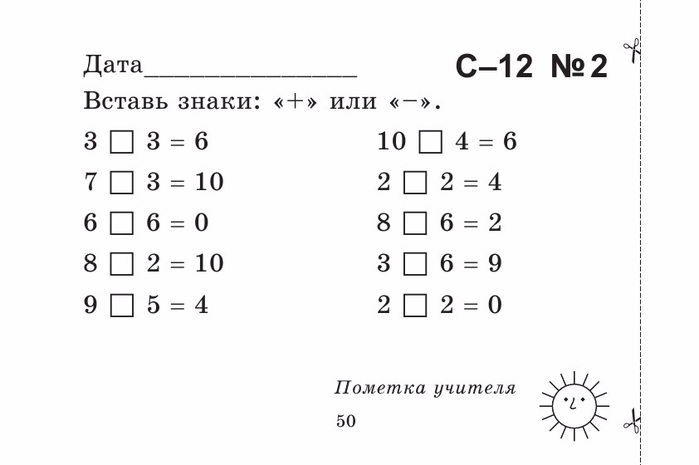 Решениями неравенства x > 4 будут все числа, которые больше 4. Граница 4 не принадлежит множеству решений, поскольку неравенство строгое.
Решениями неравенства x > 4 будут все числа, которые больше 4. Граница 4 не принадлежит множеству решений, поскольку неравенство строгое.
Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 3. Решить неравенство 3y + 1 > 1 + 6y
Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:
3y − 6y> 1 − 1
Приведём подобные слагаемые:
−3y > 0
Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства y < 0 являются все числа, меньшие нуля. Изобразим множество решений неравенства y < 0 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)
Раскроем скобки в обеих частях неравенства:
Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:
Приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 8
Решениями неравенства являются все числа, которые меньше . Граница принадлежит множеству решений, поскольку неравенство является нестрогим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство
Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:
Теперь перенесем 5 из левой части в правую часть, изменив знак:
После приведения подобных слагаемых, получим неравенство 6x > 1. Разделим обе части этого неравенства на 6. Тогда получим:
Решениями неравенства являются все числа, которые больше . Граница не принадлежит множеству решений, поскольку неравенство является строгим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 6. Решить неравенство
Умножим обе части на 6
После приведения подобных слагаемых, получим неравенство 5x < 30. Разделим обе части этого неравенства на 5
Решениями неравенства x < 6 являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x < 6 строгим.
Изобразим множество решений неравенства x < 6 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 7. Решить неравенство
Умножим обе части неравенства на 10
В получившемся неравенстве раскроем скобки в левой части:
Перенесем члены без x в правую часть
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 10
Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5. Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.
Изобр
Онлайн урок: Сравнение чисел по предмету Математика 6 класс
Вы уже познакомились с модулями чисел. Теперь надо понять, как их сравнивать с числами.
Про модуль числа нам известно, что он всегда больше или равен нулю: равен нулю, если взят от нуля, во всех остальных случаях он больше нуля.
Это знание нам и позволяет легко сравнивать модуль с другими числами.
Число может быть:
- меньше нуля
- равно нулю
- больше нуля
Рассмотрим все три варианта.
1. Сравнение модуля с отрицательным числом
Мы знаем, что отрицательные числа меньше нуля.
Также мы знаем, что отрицательные числа меньше положительных.
Значит, что бы не было внутри модуля, он сам будет больше или равен нулю, и отрицательное число окажется меньше него.
Пример:
Сравним \(\mathbf{-3}\) и \(\mathbf{\mid-54\mid}\)
Первое число- отрицательное, вторым выражением будет модуль.
Так как отрицательное число всегда меньше модуля, делаем вывод, что \(\mathbf{-3<\mid-54\mid}\)
2. Сравнение модуля с нулем
Модуль числа равен нулю тогда и только тогда, когда значение под модулем равно нулю.
Значит, чтобы понять, больше ли нуля модуль, мы должны посмотреть на значение под ним.
Пример 1
Сравним \(\mathbf{\mid-12\mid}\) и 0
Аргумент модуля не равен нулю, значит, модуль больше нуля, то есть \(\mathbf{\mid-12\mid>0}\)
Пример 2
Сравним \(\mathbf{\mid10-2\cdot5\mid}\) и 0
Посчитаем аргумент модуля.
\(\mathbf{10-2\cdot5=10-10=0}\)
Если выражение под модулем равно нулю, значит, и модуль равен нулю, так что \(\mathbf{\mid10-2\cdot5\mid=0}\)
3. Сравнение модуля с положительным числом
В этом случае сразу или почти сразу ничего сказать нельзя, придется вычислять значение модуля, а дальше сравнивать два числа с одинаковыми знаками.{3}}=6\)
А что больше? \( y\) или \( x\)? Это ты, конечно, сравнишь без всякого труда. Чем большее число мы возводим в степень, тем больше будет значение.
Итак. Выведем правило.
Если показатели степени корней одинаковы (в нашем случае это \( 3\)), то необходимо сравнивать подкоренные выражения (\( 4\) и \( 6\)) — чем больше подкоренное число, тем больше значение корня при равных показателях.
Сложно запомнить? Тогда просто держи в голове пример \( \sqrt{16}\) и \( \sqrt{4}\). Что больше?
\( \sqrt{16}=4\)
\( \sqrt{4}=2\)
\( 4\) больше \( 2\).
Показатели степени корней одинаковы, так как корень квадратный. Подкоренное выражение одного числа (\( 16\)) больше другого (\( 4\)), значит, правило действительно верное.
А что, если подкоренные выражения одинаковые, а вот степени корней разные? Например: \( \sqrt[4]{6}\vee \sqrt[3]{6}\).
Тоже вполне понятно, что при извлечении корня большей степени получится меньшее число.{6}}=12\)
Ты без труда видишь, что в данных уравнениях \( a\) должно быть больше \( b\), следовательно:
\( \sqrt[3]{12}>\sqrt[6]{12}\).
Если подкоренные выражения одинаковы (в нашем случае \( 12\)), а показатели степени корней различны (в нашем случае это \( 3\) и \( 6\)), то необходимо сравнивать показатели степени (\( 3\) и \( 6\)) — чем больше показатель, тем меньше данное выражение.
Попробуй сравнить следующие корни.
Сравним полученные результаты?
С этим благополучно разобрались :). Возникает другой вопрос: а что если у нас все разное? И степень, и подкоренное выражение?
Не все так сложно нам нужно всего- навсего… «избавиться» от корня. Да, да. Именно избавиться)
Если у нас различные и степени и подкоренные выражения, необходимо найти наименьшее общее кратное (читай раздел про целые числа) для показателей корней и возвести оба выражения в степень, равную наименьшему общему кратному.
Что мы все на словах и на словах. Приведем пример:
\( \sqrt[3]{3}\vee \sqrt[2]{5}\)
Символ больше или равно
Обозначения
краткий
способ дать
длительный
инструкция
относится к
числа и
логика.
Обозначения
сообщение
инструмент. Символы
привыкли
устранить
нужно написать
длинный, простой
язык
инструкции для
описать
расчеты
и другие
процессы.
Например,
один символ
стоит за
весь процесс
для дополнения.
Знакомый
знак плюс
устраняет
потребность в долгом
написано
объяснение
какое дополнение
средства и как
выполнить
Это.
Такой же
символы
используется во всем мире
. . .
символов
используется в
математика
универсальный .
Та же математика
символы
используется повсюду
цивилизованный
Мир. В большинстве
случаях каждый
символ дает
такой же ясный,
точное значение
каждому
читатель
независимо от того
язык
они говорят.
Самый
ценный,
большинство
часто используемый
Символы дюйма
математика . .
.
Большинство
важно, самое
часто используемый
Отношение
символы
перечисленные
ниже.
Введение в неравенства и интервальную нотацию
Неограниченные интервалы
Алгебраическое неравенство Выражения, связанные с символами ≤, <, ≥ и>., Например x≥2, читается как « x больше или равно 2». Это неравенство имеет бесконечно много решений для x . Некоторые из решений: 2, 3, 3.5, 5, 20 и 20.001. Поскольку невозможно перечислить все решения, необходима система, позволяющая четко передавать этот бесконечный набор.Два распространенных способа выражения решений неравенства — это их графическое отображение на числовой прямой. Решения алгебраического неравенства, выраженные затенением решения на числовой прямой. и используя интервальную нотацию Текстовая система выражения решений алгебраического неравенства ..
Чтобы выразить решение графически, нарисуйте числовую линию и заштрихуйте все значения, которые являются решениями неравенства. Обозначение интервалов является текстовым и использует следующие специальные обозначения:
Определите обозначение интервала после построения графика решения, установленного на числовой прямой.Числа в обозначении интервалов должны быть записаны в том же порядке, в котором они появляются в числовой строке, причем меньшие числа в наборе появляются первыми. В этом примере имеется инклюзивное неравенство Неравенство, которое включает граничную точку, обозначенную «или равной» частью символов ≤ и ≥, и замкнутую точку на числовой прямой., Что означает, что нижняя граница 2 включена в решение. Обозначьте это закрытой точкой на числовой прямой и квадратной скобкой в обозначении интервалов. Символ (∞) читается как бесконечность. Символ (∞) указывает, что интервал неограничен вправо.и указывает, что набор неограничен справа на числовой прямой. Для обозначения интервалов необходимо, чтобы бесконечность заключалась в круглые скобки. Квадратная скобка указывает на то, что граница включена в решение. Скобки указывают, что граница не включена. Бесконечность — это верхняя граница действительных чисел, но сама по себе не является действительным числом: его нельзя включить в набор решений.
Теперь сравните обозначение интервала в предыдущем примере с обозначением строгого или неисключительного неравенства, которое следует ниже:
Арифметические, относительные, логические и др.
R имеет несколько операторов для выполнения задач, включая арифметические, логические и побитовые операции.
Пример выполнения
> х <- 5
> у <- 16
> х + у
[1] 21
> х-у
[1] -11
> х * у
[1] 80
> у / х
[1] 3.Икс
[1] 1048576
R Операторы отношения
Операторы отношения используются для сравнения значений. Вот список реляционных операторов, доступных в R.
| Оператор | Описание |
|---|---|
| < | Менее |
| > | Больше |
| <= | Меньше или равно |
| > = | Больше или равно |
| == | Равно |
| ! = | Не равно |
Пример выполнения
> х <- 5
> у <- 16
> х <у
[1] ИСТИНА
> х> у
[1] ЛОЖЬ
> х <= 5
[1] ИСТИНА
> у> = 20
[1] ЛОЖЬ
> y == 16
[1] ИСТИНА
> х! = 5
[1] ЛОЖЬ
Операция с векторами
Вышеупомянутые операторы работают с векторами.Переменные, использованные выше, на самом деле были одноэлементными векторами.
Мы можем использовать функцию c () (как в concatenate) для создания векторов в R.
Все операции выполняются поэлементно. Вот пример.
> х <- с (2,8,3)
> у <- с (6,4,1)
> х + у
[1] 8 12 4
> х> у
[1] ЛОЖЬ ИСТИНА ИСТИНА
Когда существует несовпадение длины (количества элементов) векторов операндов, элементы в более коротком операнде циклически перерабатываются, чтобы соответствовать длине более длинного.
R выдаст предупреждение, если длина более длинного вектора не является целым кратным более короткого вектора.
> х <- с (2,1,8,3)
> у <- с (9,4)
> x + y # Элемент y перерабатывается в 9,4,9,4
[1] 11 5 17 7
> x-1 # Скаляр 1 переработан в 1,1,1,1
[1] 1 0 7 2
> х + с (1,2,3)
[1] 3 3 11 4
Предупреждение:
В x + c (1, 2, 3):
длина большего объекта не кратна длине более короткого объекта
R Логические операторы
Логические операторы используются для выполнения логических операций, таких как И , ИЛИ и т. Д.
| Оператор | Описание |
|---|---|
| ! | Логическое НЕ |
| и | Поэлементное логическое И |
| && | логический И |
| | | Поэлементное логическое ИЛИ |
| || | Логическое ИЛИ |
Операторы и и | выполняет поэлементную операцию с получением результата, имеющего длину более длинного операнда.
Но && и || проверяет только первый элемент операндов, в результате чего получается логический вектор одной длины.
Ноль считается ЛОЖЬ , а ненулевые числа принимаются как ИСТИНА . Пример запуска.
> x <- c (ИСТИНА, ЛОЖЬ, 0,6)
> y <- c (ЛОЖЬ, ИСТИНА, ЛОЖЬ, ИСТИНА)
>! х
[1] FALSE TRUE TRUE FALSE
> х и у
[1] FALSE FALSE FALSE TRUE
> х && у
[1] ЛОЖЬ
> х | у
[1] ИСТИНА ИСТИНА ЛОЖЬ ИСТИНА
> х || у
[1] ИСТИНА
R Операторы присвоения
Эти операторы используются для присвоения значений переменным.
| Оператор | Описание |
|---|---|
| <-, << -, = | Передача влево |
| ->, — >> | Право уступки |
Операторы <- и = могут использоваться почти взаимозаменяемо для присвоения переменной в той же среде.
Оператор << - используется для присвоения переменных в родительских средах (больше похоже на глобальное присвоение).Правые назначения, хотя и доступны, используются редко.
> х <- 5
> х
[1] 5
> х = 9
> х
[1] 9
> 10 -> х
> х
[1] 10
Посмотрите эти примеры, чтобы узнать больше:
Больше или равно
Презентация на тему: «Больше или равно» - стенограмма презентации:
1
г.Отличные студенты-алгебры Питера Ричарда будут решать сложные неравенства
2
Больше или равно
Символы неравенства Меньше Не равно Меньше или равно Больше или равно Больше
3
Преобразования для неравенств
Сложить / вычесть одно и то же число с каждой стороны неравенства Умножить / разделить на одно и то же положительное число с каждой стороны неравенства. Если вы умножаете или делите на отрицательное число, вы ДОЛЖНЫ перевернуть знак неравенства!
4
Графическое изображение линейных неравенств
Помните: знаки <и> будут иметь открытую точку o, а знаки будут иметь замкнутую точечную диаграмму графика 4 5 6 7 -3 -2 -1
5
Сложное неравенство Неравенство, соединенное «и» или «или».Примеры
думай между веслами на лодке
6
Решить и построить график. -9-9 +8 +8 -6x <-6 -3x> 21
-6x + 9 <3 или -3x-8> 13 -6x
8
Обратить оба неравенства
Пример: Решите –x + 3 <-2 или -4 - x> 5, затем построите график.–X + 3 <-2 или -4 - x> 5 -x <-5 или x> 9 x> 5 или x <-9
9
4) Изобразите составное неравенство 6
В таком виде это то же самое, что и 6
10
3) Какие неравенства описывают следующий график?
-2-1-3 o y> -3 или y <-1 y> -3 и y <-1 y ≤ -3 или y ≥ -1 y ≥ -3 и y ≤ -1
11
Решите это сами! Пример: Решите -9 ≤ -4x - 5 <3.График.
-4 ≤ -4x <8 1 ≥ x> -2
Построение графиков и решение неравенств | Ресурсы Wyzant
Решение неравенств не так уж отличается от решения обычных уравнений. По факту,
знак неравенства (<,>, ≤, ≥) рассматривается как равный
Знак (=) при решении неравенств, включающих только сложение или вычитание. Перед
все это, определим разные знаки неравенства:
- < означает, что выражение слева на меньше выражение
справа, например:означает, что 3 меньше 9, и все мы знаем, что это правда.
означает, что решение выражения слева меньше нуля, но больше
об этом позже. - > означает, что выражение слева на больше, чем ,
выражение справа, например:показывает, что 9 больше 3 и аналогично
означает, что значение 2x - 9 больше 11
- ≤ означает, что значение слева на меньше или равно .
значение справа, например:означает, что значение выражения слева должно быть меньше или равно
25 - ≥ означает, что значение слева на больше или равно
значение справа, например:
Неравенство лучше всего рассматривать как представление различных регионов на числовой прямой:
- < представляет область слева от заданного числа, например
представляет все числа слева от 3 (меньше 3), которые находятся в числе
линия ниже показана всеми числами в направлении стрелки - > представляет область справа от данного числа, например
представляет все числа справа от 3 (больше 3), которые входят в число
линия ниже показана всеми числами в направлении стрелки - ≤ представляет область от данного числа слева от того же числа,
напримерпредставляет все числа слева от 5 (меньше 5), включая саму 5 как
отображается в числовой строке под номером - ≥ представляет область от заданного числа справа от того же самого
число, например;представляет все числа слева от 1 (меньше 1), включая саму 1 как
отображается в числовой строке под номером
Устранение неравенств
Большинство линейных неравенств можно решить так же, как и линейные уравнения:
и вычитание любого числа (положительного или отрицательного) может быть выполнено с выражением
по обе стороны от неравенства без изменения самого неравенства.В другом
словами, это будет то же самое, что и в любом обычном уравнении.
Например, ; решить для x в
Решение :
Вычтем 9 из обеих частей неравенства следующим образом:
и ответ будет
Обратите внимание, что вышеуказанное решение решается так же, как решение обычных уравнений.Это связано с тем, что сложение и вычитание не влияют на знак неравенства.
Умножение и деление отличаются, однако, поскольку знак неравенства трактуется
по-разному в зависимости от того, умножаете ли вы на положительное или отрицательное число.
Умножение или деление выражения неравенства на положительное число имеет
не влияет на знак неравенства и обрабатывается как обычное уравнение.
Например, , решите относительно x в:
Решение :
Сначала прибавьте 9 к обеим сторонам неравенства
затем разделите на 3
что приводит к
Умножение или деление неравенства на отрицательное число дает эффект
изменения знака неравенства, например, с < на > как
показано ниже
решается следующим образом;
деление на -2 меняет знак неравенства на противоположное, что дает:
Чтобы доказать, почему вышесказанное верно, давайте сначала разберемся с ответом:
означает, что x может принимать любое значение, если это значение больше, чем
-4, и исходное уравнение будет верным.Чтобы доказать это, попробуем разные значения
х;
Сначала попробуйте x = 1, 1 больше -4, поэтому подставьте x = 1 в исходное выражение
должен дать математически правильное неравенство
что является правдой.
Затем давайте попробуем значение x меньше -4, например, подставим x = -5
но 7 не меньше 5, что означает, что мы получили решение x> -4
правда.Попробуйте подставить разные значения x в выражение -3 - 2x <
5 и какое бы значение вы ни выбрали, пока x> -4 решение
всегда должно быть верным.
Решение полиномиальных неравенств
Решить более сложные полиномиальные неравенства не так-то просто.
Например, , решите неравенство ниже для x
.
Решение:
Если бы это было уравнением, поиск корней факторизацией или завершением
квадрат будет всем, что нужно.Однако неравенство бывает другим. В
выше решается следующим образом:
Разложите на множители выражение слева
что означает, что либо решение выражения слева равно x = -2
или x = 6 но это еще не конец.
Затем вам нужно протестировать различные регионы на числовой строке, чтобы точно определить
где лежит решение всего неравенства.Первый тест x <-2 по
выбрав номер слева от -2 в числовой строке, а затем подставьте
в исходное неравенство, т.е.
что неверно, и поэтому мы заключаем, что x не меньше -2.
Затем мы проверяем x> -2 и, выбирая число справа от -2 на
числовая строка, но пока это число должно быть меньше 6
что верно, и поэтому мы заключаем, что x> -2 .Но так как у нас было 2 корня,
мы также должны проверить x = 6 .
Нам не нужно проверять x <6 , поскольку любое число меньше 6 также больше
чем -2, и мы уже доказали, что x> -2 . Итак, мы проверяем x> 6
что неверно, 9 не меньше нуля и, следовательно, x не больше 6.2 - 4x - 12 <0 можно представить как:
что означает, что x находится в области на числовой прямой между -2 и +6
Введение в оператор SQL Not Equal и примеры
В этой статье рассматривается оператор сравнения SQL Not Equal (<>), а также сценарии его использования.
Введение
Мы, должно быть, использовали операторы сравнения в математике в первые дни.Мы используем эти операторы для сравнения различных значений в зависимости от условий. Например, мы могли бы сравнить работу двух авторов на основе ряда статей. Предположим, Радж написал 85 статей, а Раджендра написал 100 статей. Можно сказать, что-
Общее количество статей, написанных Раджендрой> (Больше чем) от общего количества статей, написанных Раджем.
В SQL могут быть следующие операторы сравнения.
Оператор | Описание |
знак равно | Равно |
<> | Не равный |
знак равно | Не равный |
> | Больше чем |
> = | Больше, чем равно |
< | Меньше, чем |
<= | Меньше или равно |
В таблице выше мы видим, что есть два оператора для Not Equal (<> и! =).В этой статье мы рассмотрим как операторы, так и различия в них.
SQL Not Equal <> Оператор сравнения
Мы используем оператор сравнения SQL Not Equal (<>) для сравнения двух выражений. Например, операция сравнения 10 <> 11 использует оператор SQL Not Equal (<>) между двумя выражениями 10 и 11.
Разница между оператором SQL Not Equal <> и! =
Мы можем использовать оба оператора SQL Not Equal <> и! = Для проверки на неравенство между двумя выражениями.Оба оператора дают одинаковый результат. Единственное отличие состоит в том, что «<>» соответствует стандарту ISO, а «! =» Не соответствует стандарту ISO. Вы должны использовать оператор <>, поскольку он соответствует стандарту ISO.
Давайте создадим образец таблицы для изучения оператора SQL Not Equal.
CREATE TABLE dbo.Products (ProductID INT PRIMARY KEY IDENTITY (1, 1), ProductName VARCHAR (50), ProductLaunchDate DATETIME2 ); |
Для создания тестовых данных я использовал ApexSQL Generate, как показано на следующем снимке экрана.
Мы можем увидеть образцы данных в таблице «Товары».
Пример 1. Получите все сведения о продукте, кроме ProductID 1
Мы собираемся использовать оператор SQL Not Equal <>, чтобы исключить ProductID 1 из вывода.
Выберите * из dbo.products, где ProductID <> 1 |
Как было сказано ранее, мы можем использовать оператор! =, Чтобы получить тот же результат.
Выберите * из dbo.products, где ProductID! = 1 |
Пример 2: Получить список всех продуктов, кроме выпущенных в 2019 году
Предположим, мы хотим получить список продуктов, запущенных за исключением 2019 года. Мы можем использовать следующий запрос, используя оператор SQL Not Equal.
Выберите * из dbo.продукты, где Год (ProductLaunchDate) <> 2019 |
На выходе мы видим все продукты, кроме выпущенных в 2019 году.
Пример 3. Получить список всех продуктов, за исключением определенного продукта
В предыдущих примерах мы использовали SQL Not Operator и указали числовое значение в условии WHERE. Предположим, мы хотим исключить конкретный продукт из вывода. Нам нужно использовать тип данных string или varchar с одинарной кавычкой в предложении where.
Выберите * из dbo.products, где Productname <> 'Batchpickphone' |
В выводе у нас нет productID 10, так как он исключается из вывода.
Если мы не укажем выражение в одинарных кавычках, мы получим следующее сообщение об ошибке. Он обрабатывает выражения как имя столбца таблицы без одинарных кавычек.
Сообщение 207, уровень 16, состояние 1, строка 11
Недопустимое название столбца "Batchpickphone".
Пример 4: Указание нескольких условий с помощью оператора SQL Not Equal
Мы можем указать несколько условий в предложении Where, чтобы исключить соответствующие строки из вывода.
Например, мы хотим исключить ProductID 1 и ProductName Winitor (имеющий ProductID 2). Выполните следующий код, чтобы удовлетворить условию.
Выберите * из dbo.продукты, где ProductID <> 1 и ProductName <> 'Winitor' |
На выходе у нас нет ProductID 1 и ProductID 2.
Пример 5: оператор SQL Not Equal и предложение SQL Group By
Мы можем использовать оператор SQL Not Equal в сочетании с предложением SQL Group By. В следующем запросе мы используем SQL Group by on в столбце ProductLaunchDate, чтобы получить количество продуктов за исключением 2019 года.
Выберите количество (ProductLaunchDate) из dbo.Products group by ProductLaunchDate с годом (ProductLaunchDate) <> 2019 |
Анализ производительности оператора SQL Not Equal
В этой части мы рассмотрим соображения производительности оператора SQL Not Equal. В этой части оставим только 10 записей в таблице продуктов.Это помогает быстро продемонстрировать ситуацию.
Выполните следующий запрос, чтобы удалить продукты с ProductID> 10.
Удалить из продуктов, у которых ProductID> 10 |
У нас есть следующие записи в таблице «Товары».
Давайте выполним следующий запрос со следующими задачами.
- Мы используем SET STATISTICS IO ON для отображения статистики активности ввода-вывода во время выполнения запроса
- Мы используем SET STATISTICS TIME для отображения времени синтаксического анализа, компиляции и выполнения каждого оператора в пакете запроса.
- Включите план фактического выполнения, чтобы показать план выполнения, используемый для получения результатов для этого запроса оптимизатором запросов.
Установить статистику ввода-вывода Установить время статистики Выберите * из dbo.продукты, где ProductID <> 1 и Year (ProductLaunchDate) <> 2018 и ProductName <> 'Winitor' |
На вкладке сообщений мы видим, что затраченное время для этого запроса составляет 52 мс.
В фактическом плане выполнения этого запроса мы можем видеть предикаты SQL Not Equal вместе с оператором сканирования некластеризованного индекса.
Давайте перепишем этот запрос, используя оператор IN .В этом случае мы получаем такое же количество строк по сравнению с предыдущим запросом с использованием оператора SQL Not Equal.
Set Statistics IO ON Set Statistics Time On Select * from dbo.products, где ProductID in (5,6,7,8,9) |
На этот раз запрос потребовал меньше времени, чтобы вернуть то же количество строк. Это заняло всего 1 мс, тогда как запрос с SQL Not Equal занял 52 мс.
В плане фактического выполнения использовался поиск кластерного индекса, в то время как SQL Not Equal использовался
В свойстве поиска по кластеризованному индексу он использует оператор равенства для получения аналогичного набора результатов.
- Внимание: Мы должны использовать оператор равенства, чтобы получить лучшую производительность по сравнению с оператором SQL Not Equal.
Заключение
В этой статье мы рассмотрели SQL Not Operator вместе с примерами.Мы также рассмотрели его влияние на производительность по сравнению с операторами равенства. Вам следует попробовать использовать оператор равенства для повышения производительности запроса.