Путь в графе: НОУ ИНТУИТ | Лекция | Маршруты, связность, расстояния
НОУ ИНТУИТ | Лекция | Маршруты, связность, расстояния
Аннотация: Маршруты, пути, циклы. Связность и компоненты. Метрические характеристики
графов. Маршруты и связность в орграфах. Эйлеровы пути и циклы.
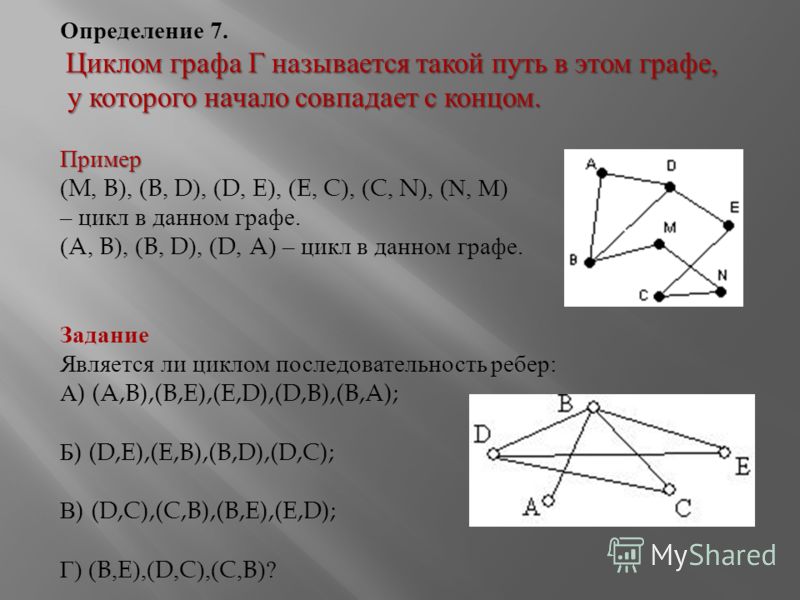
Маршруты, пути, циклы
Маршрут в графе — это
последовательность
вершин , такая, что для
каждого вершины
и соединены
ребром. Эти ребер называются ребрами маршрута.
Говорят, что маршрут проходит
через них, а число
называют длиной маршрута. Говорят,
что маршрут соединяет
вершины и , они называются
соответственно началом и концом маршрута,
вершины называются промежуточными.
Маршрут называется замкнутым,
если .
Путь — это маршрут, в котором
все ребра различны. Путь называется простым, если и все вершины в нем
различны.
Цикл — это замкнутый путь.
Цикл
называется простым, если все
вершины
попарно различны.
В графе на рисунке 2.1 последовательность вершин
Рис.
2.1.
Установим некоторые простые свойства маршрутов.
Теорема 1. В любом маршруте, соединяющем две различные вершины,
содержится простой путь, соединяющий те же вершины. В любом цикле,
проходящем через некоторое ребро, содержится простой цикл, проходящий
через это ребро.
Доказательство.
Пусть — маршрут.
Если все его вершины различны, то это уже простой путь. В противном
случае, пусть , . Тогда
последовательность ,
полученная из этого маршрута удалением отрезка
последовательности от до , тоже
является
маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину.
Продолжая действовать таким образом, после конечного числа
«спрямлений»
получим простой путь, соединяющий и .
Второе утверждение теоремы доказывается аналогично.
Отметим, что в формулировке теоремы 1 нельзя заменить слово
«цикл» словами
«замкнутый маршрут». Действительно, если — ребро
графа, то последовательность — замкнутый маршрут,
проходящий
через это ребро, но никакого цикла в нем нет.
Путь и цикл в графе — Студопедия
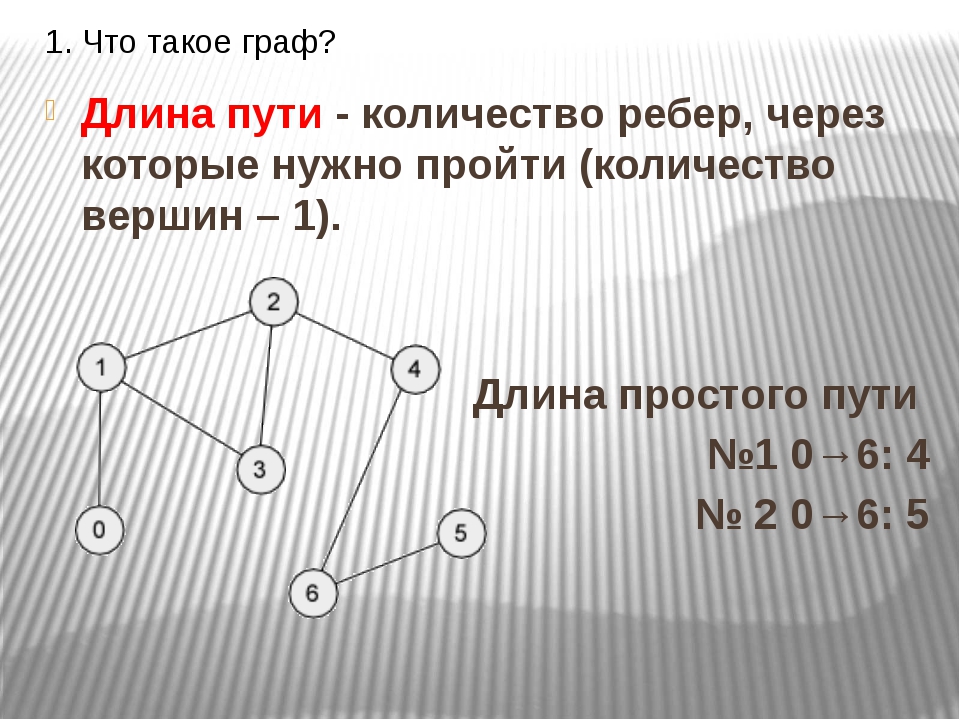
Определение 1. Путем от xi до xj называется такая последовательность ребер графа, ведущая от xi к xj , в которой два соседних ребра имеют общую вершину и никакое ребро не встречается дважды. Длиной пути называется число ребер этого пути.
Определение 2. Путь от xi до xj называется простым, если он не проходит через одну вершину более одного раза.
Пример 1. Рассмотрим граф
В данном графе есть следующие пути от x1 до x6:
1) x1, x2, x5, x6 — путь длиной 3;
2) x1, x2, x3, x5, x6 — путь длиной 4;
3) x1, x2, x4, x5, x6 — путь длиной 4;
4) x1, x2, x3, x5, x4, x2, x5, x6 — путь длиной 7.
Первые три пути являются простыми.
Определение 3. Циклом называется путь, в котором начальная и конечная вершины совпадают. Длиной цикла называется число ребер в этом цикле.
Определение 4. Цикл называется простым, если он не проходит через одну вершину более одного раза.
Пример 2.Рассмотрим граф
В данном графе есть следующие циклы:
1) x1, x5, x4, x1 — цикл длиной 3;
2) x1, x2, x3, x1 — цикл длиной 3;
3) x1, x2, x4, x5, x3, x1 — цикл длиной 5;
4) x1, x2, x4, x5, x2, x3, x1 — цикл длиной 6;
и т. д.
д.
Первые три цикла являются простыми.
Теорема.Если у графа G(X,T) все простые циклы четной длины, то граф не имеет ни одного цикла нечетной длины.
Доказательство. Предположим противное — в графе есть цикл нечетной длины. В этом цикле найдется вершина, которая повторяется дважды. В этой вершине разобьем цикл на два цикла, из которых один будет иметь четную длину, а второй — нечетную. Опять возьмем цикл нечетной длины и повторим процедуру. За конечное число шагов мы придем к простым циклам, причем один из них будет иметь нечетную длину. Получено противоречие с условием теоремы.
Маршруты, пути и циклы в графах — Студопедия
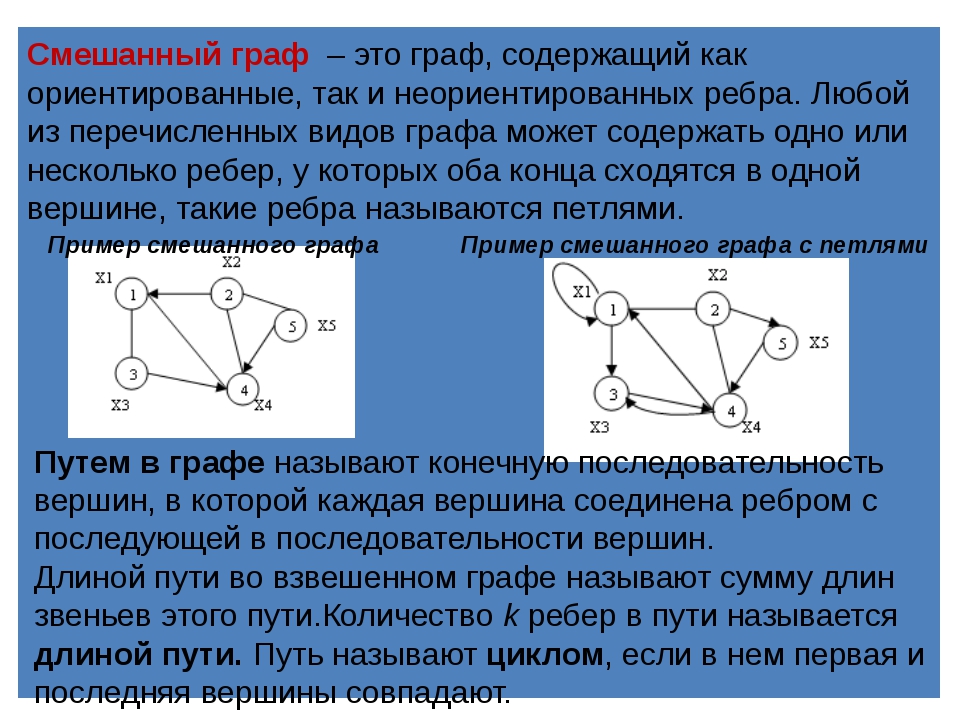
Маршрутом в графе G=(V, E) называется конечная последовательность смежных ребер вида: (v0,v1), (v1,v2), (v2,v3), ¼,(vk‑1,vk), или маршрутом можно считать такую последовательность вершин: (v0,v1,¼,vk), что любая пара вершин (vi‑1,vi), где 1£ i £ k является ребром графа G.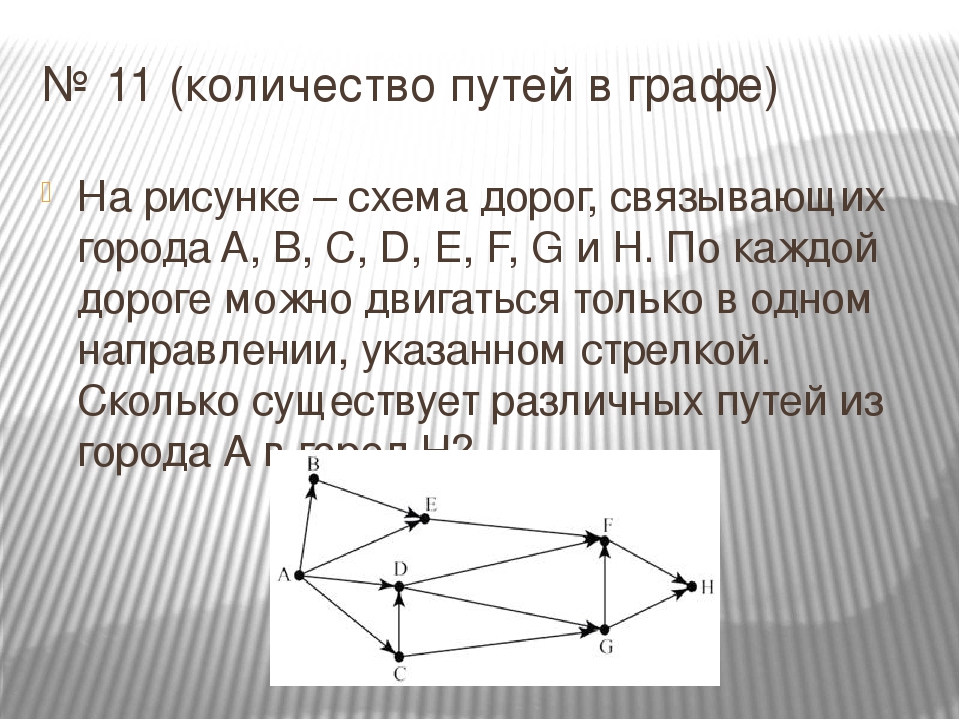 Такой маршрут называется (v0‑vk)–маршрутом, а вершины v0 и vk –начальной и конечной или терминальными вершинами маршрута. Все другие вершины маршрута называются внутренними. Заметим, что ребра и вершины в маршруте могут повторяться.
Такой маршрут называется (v0‑vk)–маршрутом, а вершины v0 и vk –начальной и конечной или терминальными вершинами маршрута. Все другие вершины маршрута называются внутренними. Заметим, что ребра и вершины в маршруте могут повторяться.
Маршрут называется открытым, если его концевые вершины различны, и замкнутым или циклическим в противном случае.
Открытый маршрут называют цепью, если все ребра в нем различны (вершины могут повторяться).
Цепь, в которой не повторяются вершины, называется путем (простой цепью).
Замкнутая цепь называется циклом, замкнутый путь – простым циклом (в орграфе – контуром). Ребро графа называется циклическим, если в графе существует цикл, содержащий это ребро.
Неорграф без циклов называется ациклическим, орграф без контуров – бесконтурным.
Длиной маршрута (пути, цикла) называется число содержащихся в нем ребер.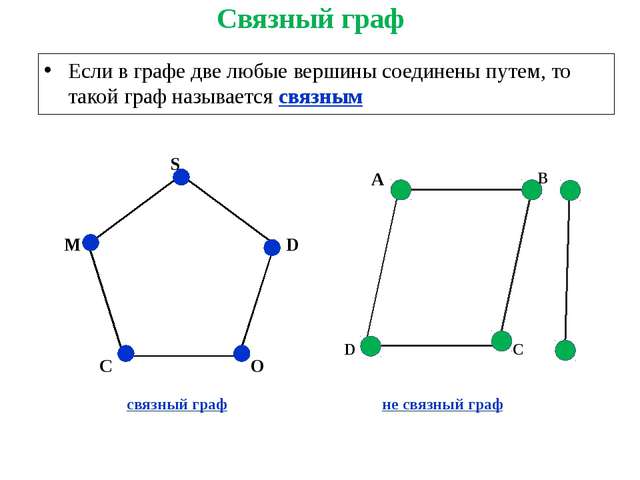 Наименьшая из длин простых циклов называется обхватом графа.
Наименьшая из длин простых циклов называется обхватом графа.
Пример:
Для графа на рис.24: открытый маршрут: (v2,v4,v1,v2,v3,v4,v1)
Замкнутый маршрут: (v2,v3,v5,v4,v3,v2)
Открытая цепь: (v2,v5,v1,v2,v4)
Замкнутая цепь (цикл): (v2,v4,v1,v2,v3,v5,v2)
Путь: (v2,v5,v1,v4,v3)
Простой цикл: (v2,v5,v1,v3,v2).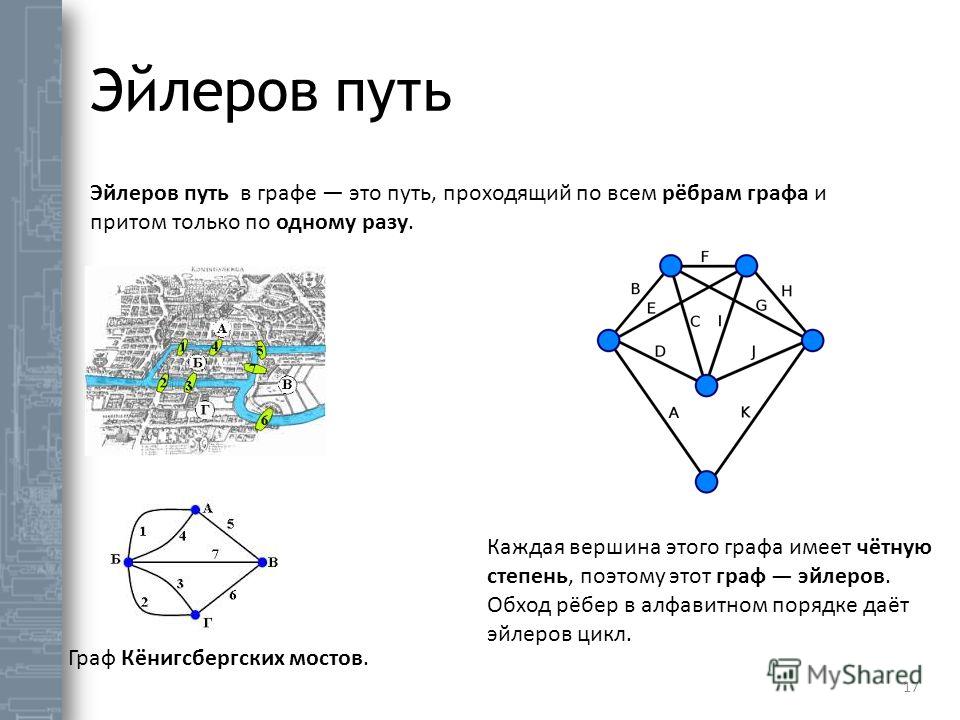 Обхват графа равен 3.
Обхват графа равен 3.
Нагруженный граф. Пути в графе. Нахождение минимального пути в графах.
Нагруженный граф – орграф G = (V, X), для которого задана функция ставящая в соответствие каждой дуге этого графа некоторое вещественное число – длина (вес) дуги x l(x). Можно задать с помощью матрицы весов:
Путь, соединяющий вершины v1 и vk в орграфе G– последовательность v1, x1, v2, x2, …, vk-1, xk-1, vk, где vi – вершина, xi=(vi,vi+1).
Замкнутый путь – путь (маршрут), у которого первая и последняя вершины совпадают. Замкнутый путь, который проходит через каждую дугу (ребро) только 1 раз называется циклом. Цикл, который проходит через каждую вершину 1 раз называется простым.
Цепь – незамкнутый путь (маршрут), который проходит через каждую дугу(ребро) только 1 раз. Цепь, которая проходит через каждую вершину 1 раз называется простой.
Цепь, которая проходит через каждую вершину 1 раз называется простой.
Длина пути (для ненагруженного графа) – количество дуг, входящих в этот путь.
Длина пути (для нагруженного графа) – сумма весов дуг, входящих в этот путь. Минимальный путь [между вершинами v1 и vk] – путь, имеющий минимальную длину среди всех других путей [из v1 в vk].
Алгоритм Дейкстры (поисл min пути в нагруженном графе)
1. Положим l*(s) = 0 и будем считать эту метку постоянной. Для всех v ОV, v № s, положим l*(v) = Ґ и будем считать эти метки временными. Положим p = s.
2. Для всех vОГp с временными метками выполним: если l*(v)>l*(p)+l(p,v), то l*(v)=l*(p)+l(p,v) и Q(v) =р. Иначе l*(v) и Q(v) не менять, т.е. l*(v) = min (l*(t), l*(p)+cpv). (Идея состоит в следующем: пусть p – вершина, получившая постоянную метку l*(p) на предыдущей итерации. Просматриваем все вершины vОГp, имеющие временные метки. Метка l*(v) вершины vОГp заменяется на l*(p)+l(p,v), если оказывается, что ее метка l*(v)>l*(p)+l(p,v). В этом случае говорим, что вершина v получила свою метку из вершины p, поэтому положим Q(v) = p. С помощью этих дополнительных меток будем потом восстанавливать сам путь. Если l*(v) Ј l*(p)+cpv, то метки остаются прежними.
Метка l*(v) вершины vОГp заменяется на l*(p)+l(p,v), если оказывается, что ее метка l*(v)>l*(p)+l(p,v). В этом случае говорим, что вершина v получила свою метку из вершины p, поэтому положим Q(v) = p. С помощью этих дополнительных меток будем потом восстанавливать сам путь. Если l*(v) Ј l*(p)+cpv, то метки остаются прежними.
3. Пусть V* — множество вершин с временными метками. Найдем вершину v* такую, что l*(v*) = min l*(v), v О V*. Считать метку l*(v*) постоянной для вершины v*.
4. Положим p = v*. Если p = t, то перейдем к п.5 ( l*(t) – длина минимального пути ). Иначе перейдем к п.2.
5. Найдем минимальный путь из s в t, используя метки Q(v): П = s…Q(t)t.
Алгоритм
— как найти самый длинный простой путь в графе?
Переполнение стека
- Около
Товары
- Для команд
Переполнение стека
Общественные вопросы и ответыПереполнение стека для команд
Где разработчики и технологи делятся частными знаниями с коллегамиВакансии
Программирование и связанные с ним технические возможности карьерного ростаТалант
Нанимайте технических специалистов и создавайте свой бренд работодателяРеклама
Обратитесь к разработчикам и технологам со всего мира- О компании
Загрузка…
Пути и цепи Эйлера
Расследуй! 35
Путь Эйлера в графе или мультиграфе — это обход графа, при котором каждое ребро используется ровно один раз.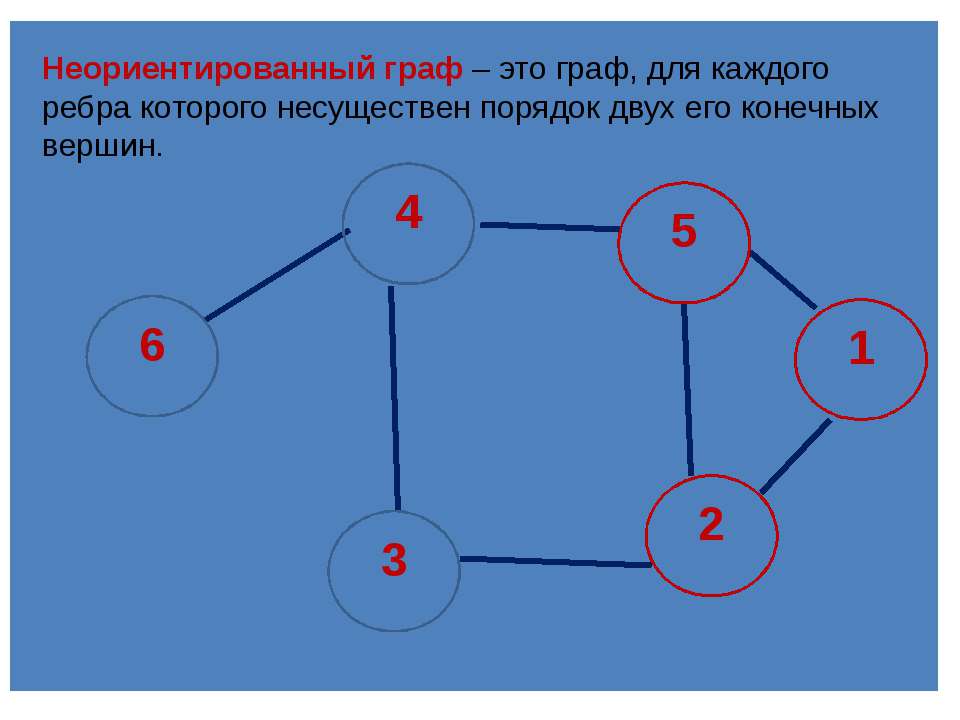 Схема Эйлера — это путь Эйлера, который начинается и заканчивается в одной и той же вершине. Наша цель — найти быстрый способ проверить, есть ли в графе (или мультиграфе) эйлеров путь или цепь.
Схема Эйлера — это путь Эйлера, который начинается и заканчивается в одной и той же вершине. Наша цель — найти быстрый способ проверить, есть ли в графе (или мультиграфе) эйлеров путь или цепь.
В каком из графов ниже есть пути Эйлера? Какие есть схемы Эйлера?
Перечислите степени каждой вершины графов выше. Есть ли связь между степенями и существованием путей и контуров Эйлера?
Может ли граф с вершиной степени 1 иметь схему Эйлера? Если да, нарисуйте один.Если нет, объясните, почему нет. А как насчет пути Эйлера?
Что делать, если каждая вершина графа имеет степень 2. Существует ли путь Эйлера? Схема Эйлера? Нарисуйте графики.
Ниже часть графика. Несмотря на то, что вы можете видеть только некоторые из вершин, можете ли вы сделать вывод, будет ли граф иметь путь Эйлера или схему?
Если мы начнем с вершины и проследим вдоль ребер, чтобы добраться до других вершин, мы создадим обход по графу. Точнее, обход в графе — это последовательность вершин, такая что каждая вершина в последовательности смежна с вершинами до и после нее в последовательности. Если прогулка проходит по каждому ребру ровно один раз, то она называется эйлеровской дорогой (или Эйлеровской ). Если, кроме того, начальная и конечная вершины совпадают (так что вы проводите вдоль каждого ребра ровно один раз и заканчиваете там, где вы начали), то обход называется контуром Эйлера (или обходом Эйлера ).Конечно, если граф не связан, нет никакой надежды найти такой путь или цепь. В оставшейся части этого раздела предполагается, что все обсуждаемые графы связаны.
Точнее, обход в графе — это последовательность вершин, такая что каждая вершина в последовательности смежна с вершинами до и после нее в последовательности. Если прогулка проходит по каждому ребру ровно один раз, то она называется эйлеровской дорогой (или Эйлеровской ). Если, кроме того, начальная и конечная вершины совпадают (так что вы проводите вдоль каждого ребра ровно один раз и заканчиваете там, где вы начали), то обход называется контуром Эйлера (или обходом Эйлера ).Конечно, если граф не связан, нет никакой надежды найти такой путь или цепь. В оставшейся части этого раздела предполагается, что все обсуждаемые графы связаны.
Мосты в Кенигсберге Проблема на самом деле вопрос о существовании путей Эйлера. Будет маршрут, который пересекает каждый мост ровно один раз тогда и только тогда, когда на графике ниже есть путь Эйлера:
Этот граф достаточно мал, чтобы мы могли проверить все возможные обходы, не использующие повторно ребра, и тем самым убедить себя, что пути Эйлера (не говоря уже о схеме Эйлера) не существует. На небольших графах, у которых есть путь Эйлера, найти его обычно не сложно. Наша цель — найти быстрый способ проверить, есть ли в графе путь Эйлера или схема, даже если граф довольно большой.
На небольших графах, у которых есть путь Эйлера, найти его обычно не сложно. Наша цель — найти быстрый способ проверить, есть ли в графе путь Эйлера или схема, даже если граф довольно большой.
Один из способов гарантировать, что граф не имеет схему Эйлера, — это включить «пик», вершину степени 1.
Вершина \ (a \) имеет степень 1, и если вы попытаетесь составить схему Эйлера, вы увидите, что застрянете в вершине. Это тупик. То есть, если вы не начнете с этого.Но тогда нет возможности вернуться, так что нет никакой надежды найти схему Эйлера. Однако существует путь Эйлера. Он начинается с вершины \ (a \ text {,} \), затем обходит треугольник. Вы закончите в вершине степени 3.
Вы сталкиваетесь с подобной проблемой всякий раз, когда у вас есть вершина любой нечетной степени. Если вы начнете с такой вершины, вы не сможете там закончить (после прохождения каждого ребра ровно один раз). После использования одного ребра для выхода из начальной вершины у вас останется четное количество ребер, исходящих из вершины. Половину из них можно было использовать для возврата в вершину, а другую половину — для ухода. Итак, вы вернетесь, а затем уйдете. Возвращайся, потом уходи. Единственный способ использовать все ребра — использовать последнее, оставив вершину. С другой стороны, если у вас есть вершина с нечетной степенью, с которой вы не начинаете путь, то в конечном итоге вы застрянете в этой вершине. Путь будет использовать пары ребер, инцидентных вершине, чтобы снова прийти и уйти. В конце концов все эти ребра, кроме одного, будут израсходованы, и останется только одно ребро, которое нужно будет пройти, и ни одно ребро не будет уходить снова.
Половину из них можно было использовать для возврата в вершину, а другую половину — для ухода. Итак, вы вернетесь, а затем уйдете. Возвращайся, потом уходи. Единственный способ использовать все ребра — использовать последнее, оставив вершину. С другой стороны, если у вас есть вершина с нечетной степенью, с которой вы не начинаете путь, то в конечном итоге вы застрянете в этой вершине. Путь будет использовать пары ребер, инцидентных вершине, чтобы снова прийти и уйти. В конце концов все эти ребра, кроме одного, будут израсходованы, и останется только одно ребро, которое нужно будет пройти, и ни одно ребро не будет уходить снова.
Все это говорит о том, что если у графа есть путь Эйлера и две вершины с нечетной степенью, то путь Эйлера должен начинаться в одной из вершин нечетной степени и заканчиваться на другой. В такой ситуации каждая вторая вершина должна иметь четную степень, поскольку нам нужно равное количество ребер, чтобы добраться до этих вершин, чтобы выйти из них. Как у нас могла быть схема Эйлера? Граф не может иметь вершину нечетной степени, поскольку путь Эйлера должен начинаться или заканчиваться там, но не то и другое вместе.Таким образом, чтобы граф имел схему Эйлера, все вершины должны иметь четную степень.
Как у нас могла быть схема Эйлера? Граф не может иметь вершину нечетной степени, поскольку путь Эйлера должен начинаться или заканчиваться там, но не то и другое вместе.Таким образом, чтобы граф имел схему Эйлера, все вершины должны иметь четную степень.
Верно и обратное: если все вершины графа имеют четную степень, то у графа есть схема Эйлера, а если есть ровно две вершины с нечетной степенью, у графа есть путь Эйлера. Доказать это немного сложно, но основная идея состоит в том, что вы никогда не застрянете, потому что для каждого «входящего» ребра в каждой вершине существует «исходящее» ребро. Если вы попытаетесь построить путь Эйлера и пропустите некоторые ребра, вы всегда сможете «соединить» схему, используя ранее пропущенные ребра.
Пути и схемы Эйлера
Поскольку в мостах графа Кенигсберга все четыре вершины имеют нечетную степень, нет пути Эйлера через граф. Таким образом, у горожан нет возможности пересечь каждый мост ровно один раз.
Подраздел Пути Гамильтона
¶
Предположим, вы хотите совершить поездку по Кенигсбергу таким образом, чтобы посетить каждый массив суши (два острова и оба берега) ровно один раз. Это можно сделать. В терминах теории графов мы спрашиваем, существует ли путь, который посещает каждую вершину ровно один раз.Такой путь называется гамильтоновым путем (или гамильтоновым путем ). Мы также могли бы рассмотреть циклов Гамильтона , которые являются путями Гамлитона, которые начинаются и заканчиваются в одной и той же вершине.
Это можно сделать. В терминах теории графов мы спрашиваем, существует ли путь, который посещает каждую вершину ровно один раз.Такой путь называется гамильтоновым путем (или гамильтоновым путем ). Мы также могли бы рассмотреть циклов Гамильтона , которые являются путями Гамлитона, которые начинаются и заканчиваются в одной и той же вершине.
Пример4.4.1
Определите, есть ли в приведенных ниже графиках путь Гамильтона.
Решение
На графике слева есть путь Гамильтона (на самом деле много разных), как показано здесь:
На графике справа нет пути Гамильтона. Вам нужно будет посетить каждую из «внешних» вершин, но как только вы посетите одну, вы застрянете.Обратите внимание, что этот граф не имеет пути Эйлера, хотя есть графы с путями Эйлера, но не пути Гамильтона.
Похоже, что найти пути Гамильтона было бы проще, потому что графы часто имеют больше ребер, чем вершин, поэтому требуется меньше требований. Однако никто не знает, правда ли это. Нет известного простого теста, есть ли у графа путь Гамильтона. Для небольших графов это не проблема, но по мере увеличения размера графа становится все труднее и труднее проверить, существует ли путь Гамильтона.Фактически, это пример вопроса, который, насколько нам известно, слишком сложно решить для компьютеров; это пример NP-полной задачи.
Нет известного простого теста, есть ли у графа путь Гамильтона. Для небольших графов это не проблема, но по мере увеличения размера графа становится все труднее и труднее проверить, существует ли путь Гамильтона.Фактически, это пример вопроса, который, насколько нам известно, слишком сложно решить для компьютеров; это пример NP-полной задачи.
Подраздел Упражнения
¶
1
Вы и ваши друзья хотите совершить поездку по юго-западу на машине. Вы посетите девять штатов, представленных ниже, со следующим довольно странным правилом: вы должны пересечь каждую границу между соседними штатами ровно один раз (так, например, вы должны пересечь границу Колорадо и Юты только один раз). Ты можешь сделать это? Если да, имеет ли значение, откуда вы начнете путешествие? Какой факт в теории графов решает эту проблему?
Решение
Это вопрос о поиске путей Эйлера.Нарисуйте граф с вершиной в каждом состоянии и соедините вершины, если их состояния имеют общую границу. Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих состояний и закончить его в другом.
Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих состояний и закончить его в другом.
2
Какой из следующих графов содержит путь Эйлера? Какие содержат схему Эйлера?
- \ (К_4 \)
- \ (K_5 \ text {.} \)
- \ (К_ {5,7} \)
- \ (К_ {2,7} \)
- \ (C_7 \)
- \ (P_7 \)
Решение
- \ (K_4 \) не имеет пути или цепи Эйлера.
- \ (K_5 \) имеет схему Эйлера (а также путь Эйлера).
- \ (K_ {5,7} \) не имеет пути или цепи Эйлера.
- \ (K_ {2,7} \) имеет путь Эйлера, но не схему Эйлера.
- \ (C_7 \) имеет схему Эйлера (это схемный граф!)
- \ (P_7 \) имеет путь Эйлера, но не схему Эйлера.
3
Эдвард А. Маус только что закончил строительство своего нового дома. План этажа показан ниже:
Эдвард хочет показать свой новый коврик подруге-мышке.
 Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начать и закончить экскурсию? Объясни.
Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начать и закончить экскурсию? Объясни.Можно ли совершить поездку по дому, посетив каждую комнату ровно один раз (не обязательно через каждый дверной проем)? Объясни.
Через несколько лет мышки Эдвард решает переделать. Он хотел бы добавить новые двери между комнатами, которые у него есть. Конечно, он не может добавлять двери в экстерьер дома. Возможно ли, чтобы в каждой комнате было нечетное количество дверей? Объясни.
4
Для какого \ (n \) граф \ (K_n \) содержит схему Эйлера? Объясни.
Решение
Когда \ (n \) нечетно, \ (K_n \) содержит схему Эйлера. Это потому, что каждая вершина имеет степень \ (n-1 \ text {,} \), поэтому при нечетном \ (n \) все степени будут четными.
5
Для каких \ (m \) и \ (n \) граф \ (K_ {m, n} \) содержит путь Эйлера? Схема Эйлера? Объясни.
Решение
Если и \ (m \), и \ (n \) четные, то \ (K_ {m, n} \) имеет схему Эйлера. Когда оба нечетные, эйлеров путь или цепь отсутствуют. Если один равен 2, а другой нечетный, то существует путь Эйлера, но не контур Эйлера.
Когда оба нечетные, эйлеров путь или цепь отсутствуют. Если один равен 2, а другой нечетный, то существует путь Эйлера, но не контур Эйлера.
6
Для какого \ (n \) \ (K_n \) содержит путь Гамильтона? Цикл Гамильтона? Объясни.
Решение
Все значения \ (n \ text {.} \) В частности, \ (K_n \) содержит \ (C_n \) в качестве подгруппы, которая представляет собой цикл, включающий каждую вершину.
7
Для каких \ (m \) и \ (n \) граф \ (K_ {m, n} \) содержит путь Гамильтона? Цикл Гамильтона? Объясни.
Решение
Пока \ (| m-n | \ le 1 \ text {,} \) граф \ (K_ {m, n} \) будет иметь путь Гамильтона. Чтобы иметь цикл Гамильтона, мы должны иметь \ (m = n \ text {.} \)
8
В Кенигсберг приехал мостостроитель и хочет добавить мосты, чтобы по каждому мосту можно было пройти ровно один раз. Сколько мостов нужно построить?
Решение
Если мы построим один мост, у нас может быть путь Эйлера. Для схемы Эйлера необходимо построить два моста.
9
Ниже приведен график, представляющий дружбу между группой студентов (каждая вершина — студент, а каждое ребро — дружба).Могут ли ученики сесть за круглый стол так, чтобы каждый ученик сидел между двумя друзьями? Какое отношение этот вопрос имеет к путям?
Решение
Мы ищем гамильтонов цикл, и на этом графике он есть:
10
Предположим, что у графа есть путь Гамильтона. Какое максимальное количество вершин первой степени может иметь граф? Объясните, почему ваш ответ правильный.
Найдите граф, в котором нет пути Гамильтона, хотя ни одна вершина не имеет степени один.Объясните, почему ваш пример работает.
11
Рассмотрим следующий график:
- Найдите путь Гамильтона. Можно ли продлить ваш путь до цикла Гамильтона?
- Является ли граф двудольным? Если да, сколько вершин в каждой «части»?
- Используйте свой ответ на часть (b), чтобы доказать, что граф не имеет цикла Гамильтона.

- Предположим, у вас есть двудольный граф \ (G \), в котором одна часть имеет как минимум на две вершины больше, чем другая. Докажите, что \ (G \) не имеет гамильтонова пути.
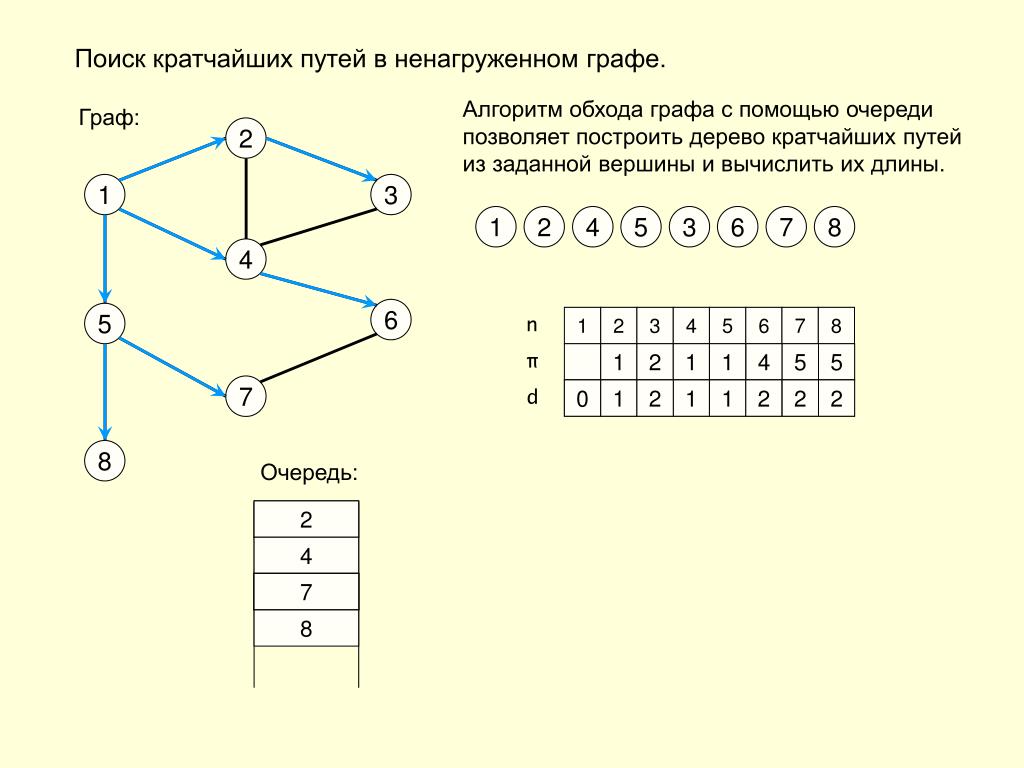
4. Алгоритмы поиска пути и графа
Поиск в ширину с Apache Spark
Реализация алгоритма поиска в ширину, реализованная в
Spark, находит кратчайший путь между двумя узлами по количеству взаимосвязей (то есть переходов) между ними. Вы можете явно назвать целевой узел или добавить критерии, которым необходимо соответствовать.
Например, мы можем использовать функцию bfs , чтобы найти первый город среднего размера (по европейским стандартам) с населением от 100 000 до 300 000 человек.Давайте сначала проверим, в каких местах население соответствует этим критериям:
(г.вершин.фильтр("население> 100000 и население <300000").
сорт(«популяция»).показать())
Вот результат, который мы увидим:
| id | широта | долгота | Население |
|---|---|---|---|
Колчестер | 51.88921 | 0, | 104390 |
Ипсвич | 52.05917 | 1.15545 | 133384 |
Есть только два места, соответствующих нашим критериям, и мы ожидаем, что первым попадем в Ипсвич на основе поиска в ширину.
Следующий код находит кратчайший путь из Гааги в город среднего размера:
from_expr="id = 'Den Haag'"to_expr="население> 100000 и население <300000 и id <> 'Den Haag'"результат=г.
bfs(from_expr,to_expr)
результат содержит столбцы, описывающие узлы и отношения между двумя городами.
Мы можем запустить следующий код, чтобы увидеть список возвращенных столбцов:
печать(результат.столбцов)
Вот результат, который мы увидим:
['from', 'e0', 'v1', 'e1', 'v2', 'e2', 'to']
Столбцы, начинающиеся с e , представляют отношения (ребра), а столбцы, начинающиеся с v , представляют узлы (вершины).Нас интересуют только узлы, поэтому давайте отфильтруем любые столбцы, начинающиеся с e , из результирующего DataFrame:
столбцов=[столбцовдлястолбцовдюймоврезультатов.
столбцыеслинестолбец.начинается с("e")]счет.выберите(столбцов).показать()
Если мы запустим код в pyspark, мы увидим следующий результат:
| из | версия 1 | версия 2 | по |
|---|---|---|---|
[Ден Хааг, 52,078… | [Хук ван Холланд… | [Felixstowe, 51,9… | [Ипсвич, 52,0591… |
Как и ожидалось, алгоритм bfs возвращает Ipswich!
Помните, что эта функция выполняется, когда она находит первое совпадение, и, как вы можете видеть на рисунке 4-3, Ипсвич оценивается раньше, чем Колчестер.
| Вычислить расстояние от источника до целевой вершины или до всех вершин от данного источника или до всех пар кратчайших путей, если источник не указан. |
| Возвращает кратчайший путь от |
| Возвращает случайный кратчайший путь от источника до цели , равномерно выбранный из всех путей равной длины. |
| Возвращает количество кратчайших путей от источника до цели . |
| Вернуть итератор по всем кратчайшим путям от источника до цели . |
| Возвращает карту свойств со всеми возможными предшественниками в дереве поиска, определенными с помощью |
| Вернуть итератор по всем путям от источника до цели . |
| Вернуть итератор по всем циклам ориентированного графа. |
| Вычислить псевдо-диаметр графа. |
| Возвращает сходство смежности между двумя графами. |
| Возвращает сходство между парами вершин. |
| Проверить, изоморфны ли два графика. |
| Получить все изоморфизмы подграфов подграфа в g (или не более max_n подграфов, если max_n> 0 ). |
| Отметить данный подграф подзаголовок на графике g . |
| Вернуть итератор по максимальным кликам графа. |
| Найдите совпадение максимального количества элементов на графике. |
| Найдите максимальное независимое множество вершин в графе. |
| Вернуть минимальное остовное дерево заданного графа. |
| Возвращает случайное остовное дерево заданного графа, которое может быть направленным или неориентированным. |
| Возвращает карту свойств вершины - доминаторные вершины для каждой вершины. |
| Вернуть топологическую сортировку данного графа. |
| Вернуть график транзитивного замыкания g. |
| Верните экскурсию коммивояжера по графу, которая гарантированно будет вдвое длиннее оптимальной в худшем случае. |
| Возвращает раскраску вершин графа. |
| Обозначьте компоненты, которым принадлежит каждая вершина в графе. |
| Обозначьте края двусвязных компонентов и вершины, которые являются точками сочленения. |
| Обозначьте самый большой компонент на графике. |
| Извлеките самый большой (сильный) компонент на графике как |
| Обозначьте исходящий компонент (или просто компонент для неориентированных графов) корневой вершины. |
| Вычислить размер самого большого или второго по величине компонента по мере (виртуального) удаления вершин из графа. |
| Вычислить размер самого большого или второго по величине компонента по мере (виртуально) удаления ребер из графа. |
| Выполнить декомпозицию по k-ядрам данного графа. |
| Проверить, является ли граф двудольным. |
| Вернуть Истинно , если граф является ориентированным ациклическим графом (DAG). |
| Проверьте, является ли график плоским. |
| Добавьте ребра в граф, чтобы сделать его максимально плоским. |
| Вычислить взаимность ребер графа. |
| ChartJS CodeMirror CSS ES6 Ворчание HTML JavaScript jQuery JWT TinyMCE Машинопись Язык программирования | C Программирование Ява PHP Python Контроль версийGit База данныхMongoDB MySQL Unix / LinuxПрограммирование оболочки Unix Vim ТестированиеМокко Мокко Чай PHPUnit КодПрограммирование Код JavaScript ДизайнЭскиз Фотошоп Подробнее. |
Поиск кратчайшего пути с ограничением вершин по большим графам
График - важная сложная сетевая модель для описания взаимосвязи между различными объектами в реальных приложениях, включая граф знаний, социальную сеть и сеть трафика.Запрос кратчайшего пути является важной проблемой для графов и хорошо изучен. В этой статье исследуется частный случай задачи о кратчайшем пути, чтобы найти кратчайший путь, проходящий через набор вершин, заданный пользователем, что является NP-трудным. Большинство существующих методов вычисляют все перестановки для заданных вершин, а затем находят самую короткую из этих перестановок. Однако вычислительные затраты чрезвычайно высоки, когда размер графа или заданного набора вершин велик. В этой статье мы сначала предлагаем новый точный эвристический алгоритм поиска лучшего первого, а затем даем два метода оптимизации для повышения эффективности.Кроме того, мы предлагаем приближенный эвристический алгоритм за полиномиальное время для этой задачи на больших графах. Мы доказываем, что оценка отношения для нашего приближенного алгоритма равна 3. Мы подтверждаем эффективность наших алгоритмов обширными экспериментами с реальными наборами данных. Результаты экспериментов подтверждают, что наши алгоритмы всегда превосходят существующие методы, даже если размер графа или заданный набор вершин велик.
1. Введение
Граф является важной сложной сетевой моделью для описания взаимосвязей между различными объектами в реальных приложениях, включая граф знаний, граф RDF, связанные данные, социальную сеть, биологическую сеть и сеть трафика [1–4 ].Запрос кратчайшего пути - основная проблема модели графа. Например, в графах знаний необходимо найти самую близкую связь между двумя сущностями или концепциями; в социальных сетях - найти самые близкие отношения, например, дружбу между двумя людьми; в транспортных сетях - вычисление кратчайшего маршрута между двумя точками.
Маршрутизация по кратчайшему пути - важная проблема в службах определения местоположения (LBS), которая была хорошо изучена в последние десятилетия [5–7].Однако особый вид запроса кратчайшего пути с вершинным ограничением становится все более и более важным в реальной жизни. Например, в графах знаний разработчик данных заинтересован в исследовании ближайших отношений между двумя сущностями, связанными некоторыми указанными сущностями или концепциями. В транспортных сетях совместное использование автомобилей становится обычным делом с быстрым развитием экономики совместного использования. Водитель автомобиля может возить некоторых товарищей по пути домой из компании, и они собираются сойти в разных местах.Таким образом, критическая проблема заключается в том, как найти маршрут с минимальной длиной, проходящий через эти места. В приведенных выше примерах и граф знаний, и сеть трафика можно смоделировать как большой граф. Запрос кратчайшего пути с ограничением вершины может быть определен следующим образом: для заданной начальной вершины, конечной вершины и подмножества найти путь с минимальной длиной среди всех путей, проходящих через каждый от до. Подмножество называется вершинным ограничением; то есть кратчайший путь должен проходить через каждую вершину в подмножестве.
Вышеупомянутая проблема является частным случаем задачи Обобщенный путь коммивояжера (GTSP) [8], которая, как известно, является NP-сложной. В задаче GTSP все вершины разбиты на несколько категорий. Цель состоит в том, чтобы найти путь, который посещает хотя бы одну вершину для каждой категории, указанной пользователем. Например, турист планирует посетить три типа мест, например, кафе, заправочную станцию и банк. Поскольку у него / нее может быть несколько вариантов выбора для каждой категории местоположения, необходимо найти для него / нее оптимальный маршрут.Основная идея большинства существующих работ по проблеме GTSP заключается в следующем: они сначала вычисляют все перестановки для заданных категорий. Каждая перестановка представляет собой класс пути, который имеет одинаковый порядок категорий. Затем для каждой перестановки эти методы перечисляют все возможные пути от источника к месту назначения, объединяя подпути между вершинами в двух последовательных категориях. Наконец, они находят оптимальный из этих путей. В нашей задаче каждая вершина в представляет категорию, отличную от других.Таким образом, эти методы должны вычислять все перестановки вершин, которые нужно посетить, что требует слишком больших вычислительных затрат. Однако большинство этих перестановок не нужны для вычисления кратчайшего пути. Следовательно, основная проблема заключается в том, как избежать вычисления ненужных перестановок при поиске кратчайшего пути с ограничением вершин. В этой статье мы предлагаем новый эффективный алгоритм, основанный на поиске лучшего первого для вычисления кратчайшего пути с ограничением вершин. Основная идея нашего метода - как можно скорее избежать вычисления ненужных перестановок.Мы также предлагаем приближенный алгоритм за полиномиальное время, который более эффективен для больших графов. Вклад этой статьи кратко излагается ниже. (I) Мы предлагаем новый и эффективный точный эвристический алгоритм с двумя методами оптимизации для поиска кратчайшего пути с ограничением вершин. (Ii) Мы также предлагаем приближенный алгоритм за полиномиальное время для нашей задачи над большие графики. Мы доказываем, что граница отношения нашего приблизительного алгоритма равна 3. (iii) Мы проводим обширные эксперименты на нескольких реальных наборах данных.Мы сравниваем наши алгоритмы с современными методами. Результаты экспериментов подтверждают эффективность и действенность наших алгоритмов.
Остальная часть этого документа организована следующим образом. В разделе 2 дается постановка проблемы. Раздел 3 знакомит с техникой CH для предварительной обработки графов. В разделе 4 предлагается алгоритм поиска лучшего первого с двумя методами оптимизации. Раздел 5 предлагает приближенный алгоритм и анализирует границу отношения. Результаты экспериментов представлены в разделе 6.Соответствующая работа находится в Разделе 7. Наконец, мы завершаем эту статью в Разделе 8.
2. Постановка задачи
Ненаправленный взвешенный граф обозначается (или для краткости), где - множество вершин, а - множество края в. - функция, присваивающая неотрицательный вес каждому ребру; т.е. Обратите внимание, что это эквивалентно, потому что это неориентированный граф. Количество вершин (или ребер) обозначается (или) в. Путь в - это последовательность вершин; т.е., где каждый является ребром для.Вес пути, обозначенный как, является суммой весов всех ребер в; т.е. Мы говорим, что путь простой тогда и только тогда, когда в нем нет повторяющейся вершины. Кратчайший путь между и - это путь с минимумом среди всех путей между и. Для простоты в дальнейшем мы используем для обозначения веса кратчайшего пути между и внутрь.
В данной статье мы изучаем задачу поиска кратчайшего пути с вершинным ограничением. В таблице 1 приведены символы в этой статье.Сначала дадим определение ниже.
| ||||||||||||||||||||||||
Кратчайший путь с ограничением 1 Определение кратчайшего пути с 1 Для данного графа, подмножества вершин, начальной вершины и конечной вершины в, путь называется кратчайшим путем между вершинами и ограничением вершин в, обозначается как, если он удовлетворяет следующим двум условиям: проходит через все вершины в ; т.
 Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начать и закончить экскурсию? Объясни.
Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начать и закончить экскурсию? Объясни.


 35
35 


 ..
..