Sklearn auc roc: sklearn.metrics.roc_auc_score — scikit-learn 0.23.2 documentation
Метрики в задачах машинного обучения / Блог компании Open Data Science / Хабр
Привет, Хабр!
В задачах машинного обучения для оценки качества моделей и сравнения различных алгоритмов используются метрики, а их выбор и анализ — непременная часть работы датасатаниста.
В этой статье мы рассмотрим некоторые критерии качества в задачах классификации, обсудим, что является важным при выборе метрики и что может пойти не так.
Для демонстрации полезных функций sklearn и наглядного представления метрик мы будем использовать датасет по оттоку клиентов телеком-оператора.
Загрузим необходимые библиотеки и посмотрим на данные
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import rc, plot
import seaborn as sns
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn. metrics import precision_recall_curve, classification_report
from sklearn.model_selection import train_test_split
df = pd.read_csv('../../data/telecom_churn.csv')
metrics import precision_recall_curve, classification_report
from sklearn.model_selection import train_test_split
df = pd.read_csv('../../data/telecom_churn.csv')
df.head(5)Предобработка данных
# Сделаем маппинг бинарных колонок
# и закодируем dummy-кодированием штат (для простоты, лучше не делать так для деревянных моделей)
d = {'Yes' : 1, 'No' : 0}
df['International plan'] = df['International plan'].map(d)
df['Voice mail plan'] = df['Voice mail plan'].map(d)
df['Churn'] = df['Churn'].astype('int64')
le = LabelEncoder()
df['State'] = le.fit_transform(df['State'])
ohe = OneHotEncoder(sparse=False)
encoded_state = ohe.fit_transform(df['State'].values.reshape(-1, 1))
tmp = pd.DataFrame(encoded_state,
columns=['state ' + str(i) for i in range(encoded_state.shape[1])])
df = pd.concat([df, tmp], axis=1)Accuracy, precision и recall
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов, тогда матрица ошибок классификации будет выглядеть следующим образом:
| True Positive (TP) | False Positive (FP) | |
| False Negative (FN) | True Negative (TN) |
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
Обучение алгоритма и построение матрицы ошибок
X = df.drop('Churn', axis=1)
y = df['Churn']
# Делим выборку на train и test, все метрики будем оценивать на тестовом датасете
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.33, random_state=42)
# Обучаем ставшую родной логистическую регрессию
lr = LogisticRegression(random_state=42)
lr. fit(X_train, y_train)
# Воспользуемся функцией построения матрицы ошибок из документации sklearn
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.
fit(X_train, y_train)
# Воспользуемся функцией построения матрицы ошибок из документации sklearn
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt. tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
font = {'size' : 15}
plt.rc('font', **font)
cnf_matrix = confusion_matrix(y_test, lr.predict(X_test))
plt.figure(figsize=(10, 8))
plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'],
title='Confusion matrix')
plt.savefig("conf_matrix.png")
plt.show()
tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
font = {'size' : 15}
plt.rc('font', **font)
cnf_matrix = confusion_matrix(y_test, lr.predict(X_test))
plt.figure(figsize=(10, 8))
plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'],
title='Confusion matrix')
plt.savefig("conf_matrix.png")
plt.show()
Accuracy
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую accuracy:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Precision, recall и F-мера
Для оценки качества работы алгоритма на каждом из классов по отдельности введем метрики precision (точность) и recall (полнота).
Precision можно интерпретировать как долю объектов, названных классификатором положительными и при этом действительно являющимися положительными, а recall показывает, какую долю объектов положительного класса из всех объектов положительного класса нашел алгоритм.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive. Recall демонстрирует способность алгоритма обнаруживать данный класс вообще, а precision — способность отличать этот класс от других классов.
Как мы отмечали ранее, ошибки классификации бывают двух видов: False Positive и False Negative. В статистике первый вид ошибок называют ошибкой I-го рода, а второй — ошибкой II-го рода. В нашей задаче по определению оттока абонентов, ошибкой первого рода будет принятие лояльного абонента за уходящего, так как наша нулевая гипотеза состоит в том, что никто из абонентов не уходит, а мы эту гипотезу отвергаем. Соответственно, ошибкой второго рода будет являться «пропуск» уходящего абонента и ошибочное принятие нулевой гипотезы.
В нашей задаче по определению оттока абонентов, ошибкой первого рода будет принятие лояльного абонента за уходящего, так как наша нулевая гипотеза состоит в том, что никто из абонентов не уходит, а мы эту гипотезу отвергаем. Соответственно, ошибкой второго рода будет являться «пропуск» уходящего абонента и ошибочное принятие нулевой гипотезы.
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Классическим примером является задача определения оттока клиентов.
Очевидно, что мы не можем находить всех уходящих в отток клиентов и только их. Но, определив стратегию и ресурс для удержания клиентов, мы можем подобрать нужные пороги по precision и recall. Например, можно сосредоточиться на удержании только высокодоходных клиентов или тех, кто уйдет с большей вероятностью, так как мы ограничены в ресурсах колл-центра.
Обычно при оптимизации гиперпараметров алгоритма (например, в случае перебора по сетке GridSearchCV ) используется одна метрика, улучшение которой мы и ожидаем увидеть на тестовой выборке.
Существует несколько различных способов объединить precision и recall в агрегированный критерий качества. F-мера (в общем случае ) — среднее гармоническое precision и recall :
в данном случае определяет вес точности в метрике, и при это среднее гармоническое (с множителем 2, чтобы в случае precision = 1 и recall = 1 иметь )
F-мера достигает максимума при полноте и точности, равными единице, и близка к нулю, если один из аргументов близок к нулю.
В sklearn есть удобная функция _metrics.classificationreport, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.
report = classification_report(y_test, lr.predict(X_test), target_names=['Non-churned', 'Churned'])
print(report)
| class | precision | recall | f1-score | support |
|---|---|---|---|---|
| Non-churned | 0. 88 88 | 0.97 | 0.93 | 941 |
| Churned | 0.60 | 0.25 | 0.35 | 159 |
| avg / total | 0.84 | 0.87 | 0.84 | 1100 |
Здесь необходимо отметить, что в случае задач с несбалансированными классами, которые превалируют в реальной практике, часто приходится прибегать к техникам искусственной модификации датасета для выравнивания соотношения классов. Их существует много, и мы не будем их касаться, здесь можно посмотреть некоторые методы и выбрать подходящий для вашей задачи.
AUC-ROC и AUC-PR
При конвертации вещественного ответа алгоритма (как правило, вероятности принадлежности к классу, отдельно см. SVM) в бинарную метку, мы должны выбрать какой-либо порог, при котором 0 становится 1. Естественным и близким кажется порог, равный 0.5, но он не всегда оказывается оптимальным, например, при вышеупомянутом отсутствии баланса классов.
Одним из способов оценить модель в целом, не привязываясь к конкретному порогу, является AUC-ROC (или ROC AUC) — площадь (Area Under Curve) под кривой ошибок (Receiver Operating Characteristic curve ). Данная кривая представляет из себя линию от (0,0) до (1,1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR):
TPR нам уже известна, это полнота, а FPR показывает, какую долю из объектов negative класса алгоритм предсказал неверно. В идеальном случае, когда классификатор не делает ошибок (FPR = 0, TPR = 1) мы получим площадь под кривой, равную единице; в противном случае, когда классификатор случайно выдает вероятности классов, AUC-ROC будет стремиться к 0.5, так как классификатор будет выдавать одинаковое количество TP и FP.
Каждая точка на графике соответствует выбору некоторого порога. Площадь под кривой в данном случае показывает качество алгоритма (больше — лучше), кроме этого, важной является крутизна самой кривой — мы хотим максимизировать TPR, минимизируя FPR, а значит, наша кривая в идеале должна стремиться к точке (0,1).
Код отрисовки ROC-кривой
sns.set(font_scale=1.5)
sns.set_color_codes("muted")
plt.figure(figsize=(10, 8))
fpr, tpr, thresholds = roc_curve(y_test, lr.predict_proba(X_test)[:,1], pos_label=1)
lw = 2
plt.plot(fpr, tpr, lw=lw, label='ROC curve ')
plt.plot([0, 1], [0, 1])
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC curve')
plt.savefig("ROC.png")
plt.show()
Критерий AUC-ROC устойчив к несбалансированным классам (спойлер: увы, не всё так однозначно) и может быть интерпретирован как вероятность того, что случайно выбранный positive объект будет проранжирован классификатором выше (будет иметь более высокую вероятность быть positive), чем случайно выбранный negative объект.
Рассмотрим следующую задачу: нам необходимо выбрать 100 релевантных документов из 1 миллиона документов. Мы намашинлернили два алгоритма:
- Алгоритм 1 возвращает 100 документов, 90 из которых релевантны.
 Таким образом,
Таким образом,
- Алгоритм 2 возвращает 2000 документов, 90 из которых релевантны. Таким образом,
Скорее всего, мы бы выбрали первый алгоритм, который выдает очень мало False Positive на фоне своего конкурента. Но разница в False Positive Rate между этими двумя алгоритмами крайне мала — всего 0.0019. Это является следствием того, что AUC-ROC измеряет долю False Positive относительно True Negative и в задачах, где нам не так важен второй (больший) класс, может давать не совсем адекватную картину при сравнении алгоритмов.
Для того чтобы поправить положение, вернемся к полноте и точности :
Здесь уже заметна существенная разница между двумя алгоритмами — 0.855 в точности!
Precision и recall также используют для построения кривой и, аналогично AUC-ROC, находят площадь под ней.
Здесь можно отметить, что на маленьких датасетах площадь под PR-кривой может быть чересчур оптимистична, потому как вычисляется по методу трапеций, но обычно в таких задачах данных достаточно. За подробностями о взаимоотношениях AUC-ROC и AUC-PR можно обратиться сюда.
За подробностями о взаимоотношениях AUC-ROC и AUC-PR можно обратиться сюда.
Logistic Loss
Особняком стоит логистическая функция потерь, определяемая как:
здесь — это ответ алгоритма на -ом объекте, — истинная метка класса на -ом объекте, а размер выборки.
Подробно про математическую интерпретацию логистической функции потерь уже написано в рамках поста про линейные модели.
Данная метрика нечасто выступает в бизнес-требованиях, но часто — в задачах на kaggle.
Интуитивно можно представить минимизацию logloss как задачу максимизации accuracy путем штрафа за неверные предсказания. Однако необходимо отметить, что logloss крайне сильно штрафует за уверенность классификатора в неверном ответе.
Рассмотрим пример:
def logloss_crutch(y_true, y_pred, eps=1e-15):
return - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
print('Logloss при неуверенной классификации %f' % logloss_crutch(1, 0.5))
>> Logloss при неуверенной классификации 0. 693147
print('Logloss при уверенной классификации и верном ответе %f' % logloss_crutch(1, 0.9))
>> Logloss при уверенной классификации и верном ответе 0.105361
print('Logloss при уверенной классификации и НЕверном ответе %f' % logloss_crutch(1, 0.1))
>> Logloss при уверенной классификации и НЕверном ответе 2.302585
693147
print('Logloss при уверенной классификации и верном ответе %f' % logloss_crutch(1, 0.9))
>> Logloss при уверенной классификации и верном ответе 0.105361
print('Logloss при уверенной классификации и НЕверном ответе %f' % logloss_crutch(1, 0.1))
>> Logloss при уверенной классификации и НЕверном ответе 2.302585Отметим, как драматически выросла logloss при неверном ответе и уверенной классификации!
Следовательно, ошибка на одном объекте может дать существенное ухудшение общей ошибки на выборке. Такие объекты часто бывают выбросами, которые нужно не забывать фильтровать или рассматривать отдельно.
Всё становится на свои места, если нарисовать график logloss:
Видно, что чем ближе к нулю ответ алгоритма при ground truth = 1, тем выше значение ошибки и круче растёт кривая.
Подытожим:
- В случае многоклассовой классификации нужно внимательно следить за метриками каждого из классов и следовать логике решения задачи, а не оптимизации метрики
- В случае неравных классов нужно подбирать баланс классов для обучения и метрику, которая будет корректно отражать качество классификации
- Выбор метрики нужно делать с фокусом на предметную область, предварительно обрабатывая данные и, возможно, сегментируя (как в случае с делением на богатых и бедных клиентов)
Полезные ссылки
- Курс Евгения Соколова: Семинар по выбору моделей (там есть информация по метрикам задач регрессии)
- Задачки на AUC-ROC от А.
 Г. Дьяконова
Г. Дьяконова - Дополнительно о других метриках можно почитать на kaggle. К описанию каждой метрики добавлена ссылка на соревнования, где она использовалась
- Презентация Богдана Мельника aka ld86 про обучение на несбалансированных выборках
Благодарности
Спасибо mephistopheies и madrugado за помощь в подготовке статьи.
Основы анализа данных на python с использованием pandas+sklearn / Хабр
Добрый день уважаемые читатели. В сегодняшней посте я продолжу свой цикл статей посвященный анализу данных на python c помощью модуля Pandas и расскажу один из вариантов использования данного модуля в связке с модулем для машинного обучения scikit-learn. Работа данной связки будет показана на примере задачи про спасенных с «Титаника". Данное задание имеет большую популярность среди людей, только начинающих заниматься анализом данных и машинным обучением.
Постановка задачи
Итак суть задачи состоит в том, чтобы с помощью методов машинного обучения построить модель, которая прогнозировала бы спасется человек или нет. К задаче прилагаются 2 файла:
К задаче прилагаются 2 файла:
- train.csv — набор данных на основании которого будет строиться модель (обучающая выборка)
- test.csv — набор данных для проверки модели
Как было написано выше, для анализ понадобятся модули Pandas и scikit-learn. С помощью Pandas мы проведем начальный анализ данных, а sklearn поможет в вычислении прогнозной модели. Итак, для начала загрузим нужные модули:
Кроме того даются пояснения по некоторым полям:
- PassengerId — идентификатор пассажира
- Survival — поле в котором указано спасся человек (1) или нет (0)
- Pclass — содержит социально-экономический статус:
- высокий
- средний
- низкий
- Name — имя пассажира
- Sex — пол пассажира
- Age — возраст
- SibSp — содержит информацию о количестве родственников 2-го порядка (муж, жена, братья, сетры)
- Parch — содержит информацию о количестве родственников на борту 1-го порядка (мать, отец, дети)
- Ticket — номер билета
- Fare — цена билета
- Cabin — каюта
- Embarked — порт посадки
- C — Cherbourg
- Q — Queenstown
- S — Southampton
Анализ входных данных
>Итак, задача сформирована и можно приступить к ее решению.
Для начала загрузим тестовую выборку и посмотрим как она выглядит::
from pandas import read_csv, DataFrame, Series
data = read_csv('Kaggle_Titanic/Data/train.csv')| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th… | female | 38 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 3 | 1 | 3 | Heikkinen, Miss. Laina Laina | female | 26 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 5 | 0 | 3 | Allen, Mr. William Henry | male | 35 | 0 | 0 | 373450 | 8.0500 | NaN | S |
Можно предположить, что чем выше социальный статус, тем больше вероятность спасения. Давайте проверим это взглянув на количество спасшихся и утонувших в зависимости в разрезе классов. Для этого нужно построить следующую сводную:
data.pivot_table('PassengerId', 'Pclass', 'Survived', 'count').plot(kind='bar', stacked=True)Наше вышеописанное предположение про то, что чем выше у пассажиров их социальное положение, тем выше их вероятность спасения. Теперь давайте взглянем, как количество родственников влияет на факт спасения:
Теперь давайте взглянем, как количество родственников влияет на факт спасения:
fig, axes = plt.subplots(ncols=2)
data.pivot_table('PassengerId', ['SibSp'], 'Survived', 'count').plot(ax=axes[0], title='SibSp')
data.pivot_table('PassengerId', ['Parch'], 'Survived', 'count').plot(ax=axes[1], title='Parch')
Как видно из графиков наше предположение снова подтвердилось, и из людей имеющих больше 1 родственников спаслись не многие.
Сейчас порассуждаем на предмет данных, которые находятся номера кают. Теоретически данных о каютах пользователей может не быть, так что давайте посмотрим на столько это поле заполнено:
data.PassengerId[data.Cabin.notnull()].count()В итоге заполнено всего 204 записи и 890, на основании этого можно сделать вывод, что данное поле при анализе можно опустить.
Следующее поле, которое мы разберем будет поле с возрастом (Age). Посмотрим на сколько оно заполнено:
data.PassengerId[data. Age.notnull()].count()
Age.notnull()].count()Данное поле практически все заполнено (714 непустых записей), но есть пустые значения, которые не определены. Давайте зададим ему значение равное медиане по возрасту из всей выборки. Данный шаг нужен для более точного построения модели:
data.Age = data.Age.median()У нас осталось разобраться с полями Ticket, Embarked, Fare, Name. Давайте посмотрим на поле Embarked, в котором находится порт посадки и проверим есть ли такие пассажиры у которых порт не указан:
data[data.Embarked.isnull()]| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 62 | 1 | 1 | Icard, Miss. Amelie | female | 28 | 0 | 0 | 113572 | 80 | B28 | NaN |
| 830 | 1 | 1 | Stone, Mrs. George Nelson (Martha Evelyn) George Nelson (Martha Evelyn) | female | 28 | 0 | 0 | 113572 | 80 | B28 | NaN |
Итак у нас нашлось 2 таких пассажира. Давайте присвоим эти пассажирам порт в котором село больше всего людей:
MaxPassEmbarked = data.groupby('Embarked').count()['PassengerId']
data.Embarked[data.Embarked.isnull()] = MaxPassEmbarked[MaxPassEmbarked == MaxPassEmbarked.max()].index[0]
Ну что же разобрались еще с одним полем и теперь у нас остались поля с имя пассажира, номером билета и ценой билета.
По сути нам из этих трех полей нам нужна только цена(Fare), т.к. она в какой-то мере определяем ранжирование внутри классов поля Pclass. Т. е. например люди внутри среднего класса могут быть разделены на тех, кто ближе к первому(высшему) классу, а кто к третьему(низший). Проверим это поле на пустые значения и если таковые имеются заменим цену медианой по цене из все выборки:
data. PassengerId[data.Fare.isnull()]
PassengerId[data.Fare.isnull()] В нашем случае пустых записей нет.
В свою очередь номер билета и имя пассажира нам никак не помогут, т. к. это просто справочная информация. Единственное для чего они могут пригодиться — это определение кто из пассажиров потенциально являются родственниками, но так как люди у которых есть родственники практически не спаслись (это было показано выше) можно пренебречь этими данными.
Теперь, после удаления всех ненужных полей, наш набор выглядит так:
data = data.drop(['PassengerId','Name','Ticket','Cabin'],axis=1)| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked |
|---|---|---|---|---|---|---|---|
| 0 | 3 | male | 28 | 1 | 0 | 7.2500 | S |
| 1 | 1 | female | 28 | 1 | 0 | 71. 2833 2833 | C |
| 1 | 3 | female | 28 | 0 | 0 | 7.9250 | S |
| 1 | 1 | female | 28 | 1 | 0 | 53.1000 | S |
| 0 | 3 | male | 28 | 0 | 0 | 8.0500 | S |
Предварительная обработка входных данных
Предварительный анализ данных завершен, и по его результатам у нас получилась некая выборка, в которой содержатся несколько полей и вроде бы можно преступить к построению модели, если бы не одно «но»: наши данные содержат не только числовые, но и текстовые данные.
Поэтому переде тем, как строить модель, нужно закодировать все наши текстовые значения.
Можно это сделать в ручную, а можно с помощью модуля sklearn.preprocessing. Давайте воспользуемся вторым вариантом.
Закодировать список с фиксированными значениями можно с помощью объекта LabelEncoder(). Суть данной функции заключается в том, что на вход ей подается список значений, который надо закодировать, на выходе получается список классов индексы которого и являются кодами элементов поданного на вход списка.
from sklearn.preprocessing import LabelEncoder
label = LabelEncoder()
dicts = {}
label.fit(data.Sex.drop_duplicates()) #задаем список значений для кодирования
dicts['Sex'] = list(label.classes_)
data.Sex = label.transform(data.Sex) #заменяем значения из списка кодами закодированных элементов
label.fit(data.Embarked.drop_duplicates())
dicts['Embarked'] = list(label.classes_)
data.Embarked = label.transform(data.Embarked)В итоге наши исходные данные будут выглядеть так:
| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked |
|---|---|---|---|---|---|---|---|
| 0 | 3 | 1 | 28 | 1 | 0 | 7.2500 | 2 |
| 1 | 1 | 0 | 28 | 1 | 0 | 71.2833 | 0 |
| 1 | 3 | 0 | 28 | 0 | 0 | 7.9250 | 2 |
| 1 | 1 | 0 | 28 | 1 | 0 | 53.1000 | 2 |
| 0 | 3 | 1 | 28 | 0 | 0 | 8.0500 | 2 |
Теперь нам надо написать код для приведения проверочного файла в нужный нам вид. Для этого можно просто скопировать куски кода которые были выше(или просто написать функцию для обработки входного файла):
test = read_csv('Kaggle_Titanic/Data/test.csv')
test.Age[test.Age.isnull()] = test.Age.mean()
test.Fare[test.Fare.isnull()] = test.Fare.median() #заполняем пустые значения средней ценой билета
MaxPassEmbarked = test.groupby('Embarked').count()['PassengerId']
test.Embarked[test.Embarked.isnull()] = MaxPassEmbarked[MaxPassEmbarked == MaxPassEmbarked.max()].index[0]
result = DataFrame(test.PassengerId)
test = test.drop(['Name','Ticket','Cabin','PassengerId'],axis=1)
label.fit(dicts['Sex'])
test.Sex = label.transform(test.Sex)
label.fit(dicts['Embarked'])
test.Embarked = label.transform(test.Embarked)
Код описанный выше выполняет практически те же операции, что мы проделали с обучающей выборкой. Отличие в том, что добавилась строка для обработки поля Fare, если оно вдруг не заполнено.
| Pclass | Sex | Age | SibSp | Parch | Fare | Embarked |
|---|---|---|---|---|---|---|
| 3 | 1 | 34.5 | 0 | 0 | 7.8292 | 1 |
| 3 | 0 | 47.0 | 1 | 0 | 7.0000 | 2 |
| 2 | 1 | 62.0 | 0 | 0 | 9.6875 | 1 |
| 3 | 1 | 27.0 | 0 | 0 | 8.6625 | 2 |
| 3 | 0 | 22.0 | 1 | 1 | 12.2875 | 2 |
Построение моделей классификации и их анализ
Ну что же, данные обработаны и можно приступить к построению модели, но для начала нужно определиться с тем, как мы будем проверять точность полученной модели. Для данной проверки мы будем использовать скользящий контроль и ROC-кривые. Проверку будем выполнять на обучающей выборке, после чего применим ее на тестовую.
Итак рассмотрим несколько алгоритмов машинного обучения:
Загрузим нужные нам библиотеки:
from sklearn import cross_validation, svm
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, auc
import pylab as pl
Для начала, надо разделить нашу обучаюшую выборку на показатель, который мы исследуем, и признаки его определяющие:
target = data.Survived
train = data.drop(['Survived'], axis=1) #из исходных данных убираем Id пассажира и флаг спасся он или нет
kfold = 5 #количество подвыборок для валидации
itog_val = {} #список для записи результатов кросс валидации разных алгоритмов
Теперь наша обучающая выборка выглядит так:
| Pclass | Sex | Age | SibSp | Parch | Fare | Embarked |
|---|---|---|---|---|---|---|
| 3 | 1 | 28 | 1 | 0 | 7.2500 | 2 |
| 1 | 0 | 28 | 1 | 0 | 71.2833 | 0 |
| 3 | 0 | 28 | 0 | 0 | 7.9250 | 2 |
| 1 | 0 | 28 | 1 | 0 | 53.1000 | 2 |
| 3 | 1 | 28 | 0 | 0 | 8.0500 | 2 |
Теперь разобьем показатели полученные ранее на 2 подвыборки(обучающую и тестовую) для расчет ROC кривых (для скользящего контроля этого делать не надо, т.к. функция проверки это делает сама. В этом нам поможет функция train_test_split модуля cross_validation:
ROCtrainTRN, ROCtestTRN, ROCtrainTRG, ROCtestTRG = cross_validation.train_test_split(train, target, test_size=0.25)
В качестве параметров ей передается:
- Массив параметров
- Массив значений показателей
- Соотношение в котором будет разбита обучающая выборка (в нашем случае для тестового набора будет выделена 1/4 часть данных исходной обучающей выборки)
На выходе функция выдает 4 массива:
- Новый обучающий массив параметров
- тестовый массив параметров
- Новый массив показателей
- тестовый массив показателей
Далее представлены перечисленные методы с наилучшими параметрами подобранные опытным путем:
model_rfc = RandomForestClassifier(n_estimators = 70) #в параметре передаем кол-во деревьев
model_knc = KNeighborsClassifier(n_neighbors = 18) #в параметре передаем кол-во соседей
model_lr = LogisticRegression(penalty='l1', tol=0.01)
model_svc = svm.SVC() #по умолчанию kernek='rbf'
Теперь проверим полученные модели с помощью скользящего контроля. Для этого нам необходимо воcпользоваться функцией cross_val_score
scores = cross_validation.cross_val_score(model_rfc, train, target, cv = kfold)
itog_val['RandomForestClassifier'] = scores.mean()
scores = cross_validation.cross_val_score(model_knc, train, target, cv = kfold)
itog_val['KNeighborsClassifier'] = scores.mean()
scores = cross_validation.cross_val_score(model_lr, train, target, cv = kfold)
itog_val['LogisticRegression'] = scores.mean()
scores = cross_validation.cross_val_score(model_svc, train, target, cv = kfold)
itog_val['SVC'] = scores.mean()
Давайте посмотрим на графике средний показатель тестов перекрестной проверки каждой модели:
DataFrame.from_dict(data = itog_val, orient='index').plot(kind='bar', legend=False)
Как можно увидеть из графика лучше всего себя показал алгоритм RandomForest. Теперь же давайте взглянем на графики ROC-кривых, для оценки точности работы классификатора. Графики будем рисовать с помощью библиотеки matplotlib:
pl.clf()
plt.figure(figsize=(8,6))
#SVC
model_svc.probability = True
probas = model_svc.fit(ROCtrainTRN, ROCtrainTRG).predict_proba(ROCtestTRN)
fpr, tpr, thresholds = roc_curve(ROCtestTRG, probas[:, 1])
roc_auc = auc(fpr, tpr)
pl.plot(fpr, tpr, label='%s ROC (area = %0.2f)' % ('SVC', roc_auc))
#RandomForestClassifier
probas = model_rfc.fit(ROCtrainTRN, ROCtrainTRG).predict_proba(ROCtestTRN)
fpr, tpr, thresholds = roc_curve(ROCtestTRG, probas[:, 1])
roc_auc = auc(fpr, tpr)
pl.plot(fpr, tpr, label='%s ROC (area = %0.2f)' % ('RandonForest',roc_auc))
#KNeighborsClassifier
probas = model_knc.fit(ROCtrainTRN, ROCtrainTRG).predict_proba(ROCtestTRN)
fpr, tpr, thresholds = roc_curve(ROCtestTRG, probas[:, 1])
roc_auc = auc(fpr, tpr)
pl.plot(fpr, tpr, label='%s ROC (area = %0.2f)' % ('KNeighborsClassifier',roc_auc))
#LogisticRegression
probas = model_lr.fit(ROCtrainTRN, ROCtrainTRG).predict_proba(ROCtestTRN)
fpr, tpr, thresholds = roc_curve(ROCtestTRG, probas[:, 1])
roc_auc = auc(fpr, tpr)
pl.plot(fpr, tpr, label='%s ROC (area = %0.2f)' % ('LogisticRegression',roc_auc))
pl.plot([0, 1], [0, 1], 'k--')
pl.xlim([0.0, 1.0])
pl.ylim([0.0, 1.0])
pl.xlabel('False Positive Rate')
pl.ylabel('True Positive Rate')
pl.legend(loc=0, fontsize='small')
pl.show()
Как видно по результатам ROC-анализа лучший результат опять показал RandomForest. Теперь осталось только применить нашу модель к тестовой выборке:
model_rfc.fit(train, target)
result.insert(1,'Survived', model_rfc.predict(test))
result.to_csv('Kaggle_Titanic/Result/test.csv', index=False)
Заключение
В данной статье я постарался показать, как можно использовать пакет pandas в связке с пакетом для машинного обучения sklearn. Полученная модель при сабмите на Kaggle показала точность 0.77033. В статье я больше хотел показать именно работу с инструментарием и ход выполнения исследования, а не построение подробного алгоритма, как например в этой серии статей.
Логистическая регрессия и ROC-анализ — математический аппарат
Введение
Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований.
Логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC-анализ почти всегда можно увидеть в наборе Data Mining алгоритмов.
Логистическая регрессия
Логистическая регрессия — это разновидность множественной регрессии, общее назначение которой состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в случае, когда зависимая переменная является бинарной (т.е. может принимать только два значения). С помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).
Все регрессионные модели могут быть записаны в виде формулы:
y = F (x_1,\, x_2, \,\dots, \, x_n)
В множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:
y = a\,+\,b_1\,x_1\,+\,b_2\,x_2\,+\,\dots\,+\,b_n\,x_n
Можно ли ее использовать для задачи оценки вероятности исхода события? Да, можно, вычислив стандартные коэффициенты регрессии. Например, если рассматривается исход по займу, задается переменная y со значениями 1 и 0, где 1 означает, что соответствующий заемщик расплатился по кредиту, а 0, что имел место дефолт.
Однако здесь возникает проблема: множественная регрессия не «знает», что переменная отклика бинарна по своей природе. Это неизбежно приведет к модели с предсказываемыми значениями большими 1 и меньшими 0.{-y}}
где P — вероятность того, что произойдет интересующее событие e — основание натуральных логарифмов 2,71…; y — стандартное уравнение регрессии.
Зависимость, связывающая вероятность события и величину y, показана на следующем графике (рис. 1):
Рис. 1 — Логистическая кривая
Поясним необходимость преобразования. Предположим, что мы рассуждаем о нашей зависимой переменной в терминах основной вероятности P, лежащей между 0 и 1. Тогда преобразуем эту вероятность P:
P’ = \log_e \Bigl(\frac{P}{1-P}\Bigr)
Это преобразование обычно называют логистическим или логит-преобразованием. Теоретически P’ может принимать любое значение. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), то эти преобразованные значения можно использовать в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии.
Существует несколько способов нахождения коэффициентов логистической регрессии. На практике часто используют метод максимального правдоподобия. Он применяется в статистике для получения оценок параметров генеральной совокупности по данным выборки. Основу метода составляет функция правдоподобия (likehood function), выражающая плотность вероятности (вероятность) совместного появления результатов выборки
L\,(Y_1,\,Y_2,\,\dots,\,Y_k;\,\theta) = p\,(Y_1;\, \theta)\cdot\dots\cdotp\,p\,(Y_k;\,\theta)
Согласно методу максимального правдоподобия в качестве оценки неизвестного параметра принимается такое значение \theta=\theta(Y_1,…,Y_k), которое максимизирует функцию L.
Нахождение оценки упрощается, если максимизировать не саму функцию L, а натуральный логарифм ln(L), поскольку максимум обеих функций достигается при одном и том же значении \theta:
L\,*\,(Y;\,\theta) = \ln\,(L\,(Y;\,\theta)\,) \rightarrow \max
В случае бинарной независимой переменной, которую мы имеем в логистической регрессии, выкладки можно продолжить следующим образом.{-1}\,g_t(W_t)\,=\,W_t\,-\,\Delta W_t
Логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой есть коэффициенты логистической регрессии, а вес поляризации — константа регрессионного уравнения (рис. 2).
Рис. 2 — Представление логистической регрессии в виде нейронной сети
Однослойная нейронная сеть может успешно решить лишь задачу линейной сепарации. Поэтому возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. Однако для оценки качества модели логистической регрессии существует эффективный инструмент ROC-анализа, что является несомненным ее преимуществом.
Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.
ROC-анализ
ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.
В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.
В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.
Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.
- TP (True Positives) — верно классифицированные положительные примеры (так называемые истинно положительные случаи).
- TN (True Negatives) — верно классифицированные отрицательные примеры (истинно отрицательные случаи).
- FN (False Negatives) — положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый «ложный пропуск» — когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры).
- FP (False Positives) — отрицательные примеры, классифицированные как положительные (ошибка II рода). Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).
Что является положительным событием, а что — отрицательным, зависит от конкретной задачи. Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным — «Здоровый пациент». И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.
При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates), выраженными в процентах:
- Доля истинно положительных примеров (True Positives Rate): TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%
- Доля ложно положительных примеров (False Positives Rate): FPR = \frac{FP}{TN\,+\,FP}\,\cdot\,100 \,\%
Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.
Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев:
S_e = TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%
Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:
S_p = \frac{TN}{TN\,+\,FP}\,\cdot\,100 \,\%
Заметим, что FPR=100-Sp
Попытаемся разобраться в этих определениях.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины — задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
- Чувствительный диагностический тест проявляется в гипердиагностике — максимальном предотвращении пропуска больных.
- Специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов не желательна.
ROC-кривая получается следующим образом:
Для каждого значения порога отсечения, которое меняется от 0 до 1 с шагом d_x (например, 0,01) рассчитываются значения чувствительности Se и специфичности Sp. В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.
Строится график зависимости: по оси Y откладывается чувствительность Se, по оси X — FPR=100-Sp — доля ложно положительных случаев.
Канонический алгоритм построения ROC-кривой
Входы: L — множество примеров f[i] — рейтинг, полученный моделью, или вероятность того, что i-й пример имеет положительный исход; min и max — минимальное и максимальное значения, возвращаемые f; d_x — шаг; P и N — количество положительных и отрицательных примеров соответственно.
- t=min
- повторять
- FP=TP=0
- для всех примеров i принадлежит L {
- если f[i]>=t тогда // этот пример находится за порогом
- если i положительный пример тогда
- { TP=TP+1 }
- иначе // это отрицательный пример
- { FP=FP+1 }
- }
- Se=TP/P*100
- point=FP/N // расчет (100 минус Sp)
- Добавить точку (point, Se) в ROC-кривую
- t=t+d_x
- пока (t>max)
В результате вырисовывается некоторая кривая (рис.2): для каждого порога необходимо «пробегать» по записям и каждый раз рассчитывать TP и FP. Если же двигаться вниз по набору данных, отсортированному по убыванию выходного поля классификатора (рейтингу), то можно за один проход вычислить значения всех точек ROC-кривой, последовательно обновляя значения TP и FP.
Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.
При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.
Рис. 4 — Сравнение ROC-кривых
Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0,5 («бесполезный» классификатор) до 1,0 («идеальная» модель).
Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5). Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций:
AUC = \int f(x)\,dx = \sum_i \Bigl[ \frac{X_{i+1}\,+\,X_i}{2}\Bigr]\,\cdot \,(Y_{i+1}\,-\, Y_i)
Рис. 5 — Площадь под ROC-кривой
С большими допущениями можно считать, что чем больше показатель AUC, тем лучшей прогностической силой обладает модель. Однако следует знать, что:
- показатель AUC предназначен скорее для сравнительного анализа нескольких моделей;
- AUC не содержит никакой информации о чувствительности и специфичности модели.
В литературе иногда приводится следующая экспертная шкала для значений AUC, по которой можно судить о качестве модели:
Идеальная модель обладает 100% чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).
Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:
- Требование минимальной величины чувствительности (специфичности) модели. Например, нужно обеспечить чувствительность теста не менее 80%. В этом случае оптимальным порогом будет максимальная специфичность (чувствительность), которая достигается при 80% (или значение, близкое к нему «справа» из-за дискретности ряда) чувствительности (специфичности).
- Требование максимальной суммарной чувствительности и специфичности модели, т.е. Cutt\underline{\,\,\,}off_o = \max_k (Se_k\,+\,Sp_k)
- Требование баланса между чувствительностью и специфичностью, т.е. когда Se \approx Sp: Cutt\underline{\,\,\,}off_o = \min_k \,\bigl |Se_k\,-\,Sp_k \bigr |
Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность или специфичность модели (рис. 6).
Рис. 6 — «Точка баланса» между чувствительностью и специфичностью
Существуют и другие подходы, когда ошибкам I и II рода назначается вес, который интерпретируется как цена ошибок. Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.
Литература
- Цыплаков А. А. Некоторые эконометрические методы. Метод максимального правдоподобия в эконометрии. Учебное пособие.
- Fawcett T. ROC Graphs: Notes and Practical Considerations for Researchers // 2004 Kluwer Academic Publishers.
- Zweig M.H., Campbell G. ROC Plots: A Fundamental Evaluation Tool in Clinical Medicine // Clinical Chemistry, Vol. 39, No. 4, 1993.
- Davis J., Goadrich M. The Relationship Between Precision-Recall and ROC Curves // Proc. Of 23 International Conference on Machine Learning, Pittsburgh, PA, 2006.
Другие материалы по теме:
Применение логистической регрессии в медицине и скоринге
Machine learning в Loginom на примере задачи c Kaggle
Машинное обучение — показатели производительности
Существуют различные метрики, которые мы можем использовать для оценки производительности алгоритмов ML, классификации, а также алгоритмов регрессии. Мы должны тщательно выбирать метрики для оценки эффективности ОД, потому что —
То, как производительность алгоритмов ML измеряется и сравнивается, будет полностью зависеть от выбранного вами показателя.
То, как вы оцениваете важность различных характеристик в результате, будет полностью зависеть от выбранной вами метрики.
То, как производительность алгоритмов ML измеряется и сравнивается, будет полностью зависеть от выбранного вами показателя.
То, как вы оцениваете важность различных характеристик в результате, будет полностью зависеть от выбранной вами метрики.
Метрики производительности для задач классификации
Мы обсуждали классификацию и ее алгоритмы в предыдущих главах. Здесь мы собираемся обсудить различные метрики производительности, которые можно использовать для оценки прогнозов для задач классификации.
Матрица путаницы
Это самый простой способ измерить производительность задачи классификации, когда выходные данные могут быть двух или более типов классов. Матрица путаницы — это не что иное, как таблица с двумя измерениями, а именно. «Фактические» и «Предсказанные», и, кроме того, оба измерения имеют «Истинные позитивы (TP)», «Истинные негативы (TN)», «Ложные позитивы (FP)», «Ложные негативы (FN)», как показано ниже —
Пояснения терминов, связанных с матрицей путаницы, следующие:
True Positives (TP) — это тот случай, когда фактический класс и прогнозируемый класс точки данных равны 1.
True Negatives (TN) — это тот случай, когда фактический класс и прогнозируемый класс точки данных равны 0.
Ложные срабатывания (FP) — это тот случай, когда фактический класс точки данных равен 0, а прогнозируемый класс точки данных равен 1.
False Negatives (FN) — это тот случай, когда фактический класс точки данных равен 1, а прогнозируемый класс точки данных равен 0.
True Positives (TP) — это тот случай, когда фактический класс и прогнозируемый класс точки данных равны 1.
True Negatives (TN) — это тот случай, когда фактический класс и прогнозируемый класс точки данных равны 0.
Ложные срабатывания (FP) — это тот случай, когда фактический класс точки данных равен 0, а прогнозируемый класс точки данных равен 1.
False Negatives (FN) — это тот случай, когда фактический класс точки данных равен 1, а прогнозируемый класс точки данных равен 0.
Мы можем использовать функцию confusion_matrix в sklearn.metrics для вычисления Confusion Matrix нашей модели классификации.
Точность классификации
Это наиболее распространенная метрика производительности для алгоритмов классификации. Это может быть определено как число правильных прогнозов, сделанных как отношение всех сделанных прогнозов. Мы можем легко рассчитать его по матрице путаницы с помощью следующей формулы —
Точность= гидроразрываTP+TNTP+FP+FN+TN
Мы можем использовать функцию precision_score sklearn.metrics, чтобы вычислить точность нашей модели классификации.
Классификационный отчет
Этот отчет состоит из оценок Точности, Напомним, F1 и Поддержки. Они объясняются следующим образом —
точность
Точность, используемая при поиске документов, может быть определена как количество правильных документов, возвращаемых нашей моделью ML. Мы можем легко рассчитать его по матрице путаницы с помощью следующей формулы —
Точность= гидроразрываTPTP+FN
Напомним или Чувствительность
Отзыв может быть определен как число положительных результатов, возвращаемых нашей моделью ML. Мы можем легко вычислить его по матрице смешения с помощью следующей формулы.
Напомним= гидроразрываTPTP+FN
специфичность
Специфичность, в отличие от напоминания, может быть определена как количество негативов, возвращаемых нашей моделью ML. Мы можем легко рассчитать его по матрице путаницы с помощью следующей формулы —
Специфичность= гидроразрываTNTN+FP
Служба поддержки
Поддержка может быть определена как количество выборок истинного ответа, который лежит в каждом классе целевых значений.
Счет F1
Эта оценка даст нам гармоничное среднее точность и отзыв. Математически, оценка F1 — средневзвешенное значение точности и отзыва. Наилучшее значение F1 будет равно 1, а худшее — 0. Мы можем рассчитать показатель F1 с помощью следующей формулы:
F1=2∗(точность∗вызов)/(точность+отзыв)
Счет F1 имеет равный относительный вклад точности и отзыва.
Мы можем использовать функциюification_report в sklearn.metrics, чтобы получить отчет о классификации нашей модели классификации.
AUC (площадь под кривой ROC)
AUC (область под кривой) -ROC (рабочая характеристика приемника) — это показатель производительности, основанный на различных пороговых значениях, для задач классификации. Как следует из названия, ROC — это кривая вероятности, а AUC измеряет отделимость. Проще говоря, метрика AUC-ROC расскажет нам о способности модели различать классы. Чем выше AUC, тем лучше модель.
Математически это может быть создано путем построения графика TPR (True Positive Rate), т. Е. Чувствительности или отзыва по сравнению с FPR (False Positive Rate), т.е. 1-специфичность, при различных пороговых значениях. Ниже приведен график, показывающий ROC, AUC, имеющий TPR на оси Y и FPR на оси X —
Мы можем использовать функцию roc_auc_score sklearn.metrics для вычисления AUC-ROC.
LOGLOSS (логарифмическая потеря)
Это также называется потерей логистической регрессии или потерей перекрестной энтропии. Он в основном определяется по оценкам вероятности и измеряет эффективность модели классификации, где входными данными является значение вероятности в диапазоне от 0 до 1. Это можно понять более четко, дифференцируя его с точностью. Поскольку мы знаем, что точность — это количество прогнозов (прогнозируемое значение = фактическое значение) в нашей модели, тогда как Log Loss — это количество неопределенности нашего прогноза, основанное на том, насколько оно отличается от фактической метки. С помощью значения Log Loss мы можем получить более точное представление о производительности нашей модели. Мы можем использовать функцию log_loss sklearn.metrics, чтобы вычислить Log Loss.
пример
Ниже приведен простой рецепт в Python, который даст нам представление о том, как мы можем использовать вышеописанные метрики производительности в бинарной модели классификации.
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
from sklearn.metrics import log_loss
X_actual = [1, 1, 0, 1, 0, 0, 1, 0, 0, 0]
Y_predic = [1, 0, 1, 1, 1, 0, 1, 1, 0, 0]
results = confusion_matrix(X_actual, Y_predic)
print ('Confusion Matrix :')
print(results)
print ('Accuracy Score is',accuracy_score(X_actual, Y_predic))
print ('Classification Report : ')
print (classification_report(X_actual, Y_predic))
print('AUC-ROC:',roc_auc_score(X_actual, Y_predic))
print('LOGLOSS Value is',log_loss(X_actual, Y_predic))Выход
Confusion Matrix :
[[3 3]
[1 3]]
Accuracy Score is 0.6
Classification Report :
precision recall f1-score support
0 0.75 0.50 0.60 6
1 0.50 0.75 0.60 4
micro avg 0.60 0.60 0.60 10
macro avg 0.62 0.62 0.60 10
weighted avg 0.65 0.60 0.60 10
AUC-ROC: 0.625
LOGLOSS Value is 13.815750437193334
Метрики производительности для задач регрессии
Мы обсуждали регрессию и ее алгоритмы в предыдущих главах. Здесь мы собираемся обсудить различные показатели производительности, которые можно использовать для оценки прогнозов для проблем регрессии.
Средняя абсолютная ошибка (MAE)
Это самый простой показатель ошибки, используемый в задачах регрессии. Это в основном сумма среднего абсолютной разницы между прогнозируемыми и фактическими значениями. Проще говоря, с помощью MAE мы можем получить представление о том, насколько неправильными были прогнозы. MAE не указывает направление модели, то есть не указывает на недостаточную или недостаточную производительность модели. Ниже приведена формула для расчета MAE —
MAE= frac1n sum midY− hatY mid
Здесь y = фактические выходные значения
И hatY = прогнозируемые выходные значения.
Мы можем использовать функцию mean_absolute_error в sklearn.metrics для вычисления MAE.
Среднеквадратичная ошибка (MSE)
MSE похож на MAE, но единственное отличие состоит в том, что он возводит в квадрат разницу фактических и прогнозируемых выходных значений перед суммированием их всех вместо использования абсолютного значения. Разницу можно заметить в следующем уравнении —
СКО= гидроразрыва1N сумма(Y− шлемY)
Здесь Y = фактические выходные значения
И hatY = прогнозируемые выходные значения.
Мы можем использовать функцию mean_squared_error в sklearn.metrics для вычисления MSE.
R в квадрате (R 2 )
R Квадратная метрика обычно используется для пояснительных целей и обеспечивает индикацию достоверности или соответствия набора прогнозируемых выходных значений фактическим выходным значениям. Следующая формула поможет нам понять это —
R2=1− frac frac1n sumni=1(Yi− hatYi)2 frac1n sumni=1(Yi− hatYi)2
В приведенном выше уравнении числитель — это MSE, а знаменатель — это дисперсия значений Y.
Мы можем использовать функцию r2_score sklearn.metrics для вычисления значения R в квадрате.
пример
Ниже приведен простой рецепт в Python, который даст нам представление о том, как мы можем использовать вышеописанные метрики производительности в регрессионной модели:
Многоклассовая классификация нейросетью — Я и программист
В этом посте я приведу простой пример мультиклассовой классификации данных с помощью нейронной сети. В качестве сети мы будем использовать многослойный перцептрон, а данными послужит набор о цветках ириса.
В 1936 году известный английский статистик, биолог и генетик Рональд Фишер продемонстрировал свой метод дискриминантного анализа на примере собранных данных о видах ириса, о длине и ширине лепестков и чашелистиков. Этот набор данных уже стал классическим и часто используется для демонстрации работы методов классификации.
Итак, приступим. Для начала инициализируем генератор случайных чисел. Это хорошая практика, позволяющая получить подобные результаты при повторении экспериментов в дальнейшем.
seed = 101
np.random.seed(seed)
seed = 101 np.random.seed(seed) |
Теперь нужно загрузить датасет. Этот сет можно найти по адресу https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data . Для работы с датасетом мы будем использовать pandas.
dataframe = pd.read_csv(‘https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data’, header=None)
dataset = dataframe.values
X = dataset[:, 0:4].astype(float)
Y = dataset[:, 4]
dataframe = pd.read_csv(‘https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data’, header=None) dataset = dataframe.values X = dataset[:, 0:4].astype(float) Y = dataset[:, 4] |
После загрузки датасета, мы делим его на две части – на целевую переменную Y и на данные, от которых она зависит X.
Мы будем определять класс растения по четырем параметрам: длине и ширине лепестка и длине и ширине чашелистика. Результирующих классов в нашем датасете три.
Визуализируем данные, для лучшего понимания:
Целевая переменная – класс, который представлен в датасете текстом. Чтобы нейросеть работала, нам нужно закодировать эти классы в целочисленные категории.
Iris-setosa кодируется как класс 0, Iris-versicolor – класс 1 и Iris-virginica как класс 2. Далее применим one-hot кодирование к полученным категориями. Iris-setosa станет [1, 0, 0], Iris-versicolor – [0, 1, 0] и т.д. Этот метод часто применяется в задачах классификации.
encoder = LabelEncoder()
encoder.fit(Y)
encoded_Y = encoder.transform(Y)
dummy_y = np_utils.to_categorical(encoded_Y)
encoder = LabelEncoder() encoder.fit(Y) encoded_Y = encoder.transform(Y) dummy_y = np_utils.to_categorical(encoded_Y) |
Нам нужно отделить часть данных для тестового подмножества для оценки качества работы нашей сети. Это удобно сделать, вызвав метод train_test_split. В качестве параметров укажем размер тестового сета – 25% и передадим наш инициализатор случайных значений.
X_train, X_test, Y_train, Y_test = train_test_split(X, dummy_y, test_size=.25, random_state=seed)
X_train, X_test, Y_train, Y_test = train_test_split(X, dummy_y, test_size=.25, random_state=seed) |
Теперь опишем нашу нейросеть. Мы используем классы из библиотека Keras. Создадим нейросеть следующей архитектуры: 4 входа под каждый признак, 4 нейрона в скрытом слое, и три выхода — по количеству классов. Вопрос архитектуры сетей до сих пор не является решенным, выбор конфигурации, как правило, основывается на опыте и оптимизируется с помощью экспериментов.
def my_model():
model = Sequential()
model.add(Dense(4, input_dim=4, init=’normal , activation= relu ))
model.add(Dense(3, init= normal , activation= sigmoid ))
model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’])
return model
def my_model(): model = Sequential() model.add(Dense(4, input_dim=4, init=’normal , activation= relu )) model.add(Dense(3, init= normal , activation= sigmoid )) model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’]) return model |
Мы готовы запустить расчет. Выполним метод fit у нашей модели. Установим количество эпох обучения равное 200 и количество примеров для одновременного обучения равное 7. Параметр verbose отвечает за вывод процесса обучения в терминал.
model = my_model()
model.fit(X_train, Y_train, batch_size=7, nb_epoch=200, verbose=1)
model = my_model() model.fit(X_train, Y_train, batch_size=7, nb_epoch=200, verbose=1) |
Оценим качество нашей модели на тестовом подмножестве. Будем использовать метрику площади под ROC-кривой. Эта метрика чаще всего применяется в задачах мультиклассовой классификации.
predictions = model.predict_proba(X_test)
print(‘Accuracy: {}’.format(roc_auc_score(y_true=Y_test, y_score=predictions)))
predictions = model.predict_proba(X_test) print(‘Accuracy: {}’.format(roc_auc_score(y_true=Y_test, y_score=predictions))) |
Запустив обучение и получив результат, можно обратить внимание на то, что на последней эпохе точность была равна acc: 0.9732, а на тестовом подмножестве она опустилась до 0.8339. Это объясняется переобучением нейросети. Сеть просто запомнила значения признаков и выдала соответственный результат на обучающем подмножестве. А так как про тестовый сет нейросеть ничего не знает, то точность на нем гораздо ниже.
Для борьбы с переобучением существует множество методик, и это темы для отдельных статей. А сейчас, чтобы немного улучшить точность можно добавить один Dropout слой между полносвязными слоями Dense. Этот слой будет вносить случайные искажения в расчет и, таким образом, будет мешать переобучению сети.
model.add(Dense(4, input_dim=4, init=’normal’, activation=’relu’))
model.add(Dropout(0.2))
model.add(Dense(3, init=’normal’, activation=’sigmoid’))
model.add(Dense(4, input_dim=4, init=’normal’, activation=’relu’)) model.add(Dropout(0.2)) model.add(Dense(3, init=’normal’, activation=’sigmoid’)) |
После запуска вы увидите, что точность неплохо возросла.
Как вы могли заметить, нейросетевой классификатор на keras реализуется довольно просто. C отступами строк, комментариями и импортами мы уложились в 50 строчек кода.
Ниже представлен полный код примера.
import numpy as np
import pandas as pd
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.utils import np_utils
from sklearn.metrics import roc_auc_score
from sklearn.preprocessing import LabelEncoder
from sklearn.cross_validation import train_test_split
# random seed
seed = 101
np.random.seed(seed)
# load and split data
dataframe = pd.read_csv(‘https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data’, header=None)
dataset = dataframe.values
X = dataset[:, 0:4].astype(float)
Y = dataset[:, 4]
# encode class values as integers
encoder = LabelEncoder()
encoder.fit(Y)
encoded_Y = encoder.transform(Y)
# one-hot
dummy_y = np_utils.to_categorical(encoded_Y)
# split to test and train
X_train, X_test, Y_train, Y_test = train_test_split(X, dummy_y, test_size=.25, random_state=seed)
# define model
def my_model():
model = Sequential()
model.add(Dense(4, input_dim=4, init=’normal’, activation=’relu’))
model.add(Dropout(0.2))
model.add(Dense(3, init=’normal’, activation=’sigmoid’))
model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’])
return model
# fit
model = my_model()
model.fit(X_train, Y_train, batch_size=7, nb_epoch=200, verbose=1)
# predict
predictions = model.predict_proba(X_test)
print(‘Accuracy: {}’.format(roc_auc_score(y_true=Y_test, y_score=predictions)))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | import numpy as np import pandas as pd from keras.models import Sequential from keras.layers import Dense, Dropout from keras.utils import np_utils from sklearn.metrics import roc_auc_score from sklearn.preprocessing import LabelEncoder from sklearn.cross_validation import train_test_split
# random seed seed = 101 np.random.seed(seed)
# load and split data dataframe = pd.read_csv(‘https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data’, header=None) dataset = dataframe.values X = dataset[:, 0:4].astype(float) Y = dataset[:, 4]
# encode class values as integers encoder = LabelEncoder() encoder.fit(Y) encoded_Y = encoder.transform(Y)
# one-hot dummy_y = np_utils.to_categorical(encoded_Y)
# split to test and train X_train, X_test, Y_train, Y_test = train_test_split(X, dummy_y, test_size=.25, random_state=seed)
# define model def my_model(): model = Sequential() model.add(Dense(4, input_dim=4, init=’normal’, activation=’relu’)) model.add(Dropout(0.2)) model.add(Dense(3, init=’normal’, activation=’sigmoid’)) model.compile(loss=’categorical_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’]) return model
# fit model = my_model() model.fit(X_train, Y_train, batch_size=7, nb_epoch=200, verbose=1)
# predict predictions = model.predict_proba(X_test) print(‘Accuracy: {}’.format(roc_auc_score(y_true=Y_test, y_score=predictions))) |
Поделиться:
Основные метрики задач классификации в машинном обучении
В каждой задаче машинного обучения ставится вопрос оценки результатов моделей.
Без введенных критериев, невозможно будет ни оценить “успешность” модели, ни сравнить между собой два различных алгоритма. Именно поэтому важно учесть правильный выбор метрик для поставленной задачи, хотя множество существующих метрик может запутать и, в конечном счете, привести к неоптимальному решению.
Несмотря на популярность машинного обучения, во многих её сферах до сих пор не сформировалась единая теоретическая концепция. Исключением не стала и рассматриваемая область. Хоть и существуют некоторые общие рекомендации к применению метрик для некоторых задач, конечное решение лежит на плечах аналитика.
Бинарная классификация
Знакомство с этим фундаментальным разделом стоит начать с изучения способов оценки одной из наиболее популярной постановки задачи — бинарной классификации. В данном случае, данные поделены всего на два класса. Их метки принято обозначать как «+» и «-». Рассматриваемые нами метрики основаны на использовании следующих исходов: истинно положительные (TP), истинно отрицательные (TN), ложно положительные (FP) и ложно отрицательные (FN). Для наглядности, можно преобразовать в таблицу сопряженности (Рисунок 1). Ложно положительный и истинно отрицательный исход ещё называют ошибками первого и второго рода соответственно.
Возьмём к примеру задачу выявления подозрения на определенное заболевание. Если у пациента оно есть, то это будет положительным классом. Если нет – отрицательным. Результатом работы модели может быть определение – следует ли «заподозрить» у пациента какой-то определенный диагноз (тогда результат = true) или нет (тогда результат = false).
Пусть какой-то набор медицинских данных характерен для данного диагноза. Если наша модель верно определила и поставила положительный класс, тогда это истинно положительный исход, если же модель ставит отрицательную метку класса, тогда это ложно отрицательный исход. В случае отсутствия диагноза у рассматриваемого набора данных исходы модели остаются аналогичными. Тогда если модель относит запись к классу положительную, то мы говорим о ложно положительном исходе (модель «сказала» что диагноз есть, но на самом деле его нет), и наоборот, если модель определят запись как отрицательный класс, то это — истинно отрицательный исход.
Рисунок 1: Матрица сопряженности возможных результатов бинарной классификации
Accuracy
Одной из наиболее простых, а поэтому и распространенной метрикой является точность. Она показывает количество правильно проставленных меток класса (истинно положительных и истинно отрицательных) от общего количества данных и считается следующим образом [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
Однако, эта простота является также и причиной, почему её часто критикуют и почему она может абсолютно не подойти под решаемую задачу. Она не учитывает соотношения ложных срабатываний модели, что может быть критическим, особенно в медицинской сфере, когда стоит задача распознать все истинные случаи диагноза.
Вернемся к примеру с подозрением на заболевание. Если наша точность равна 80%, то можно сказать, что в среднем из 100 человек она правильно определит наличие или отсутствие диагноза лишь у 80 человек, тогда как ещё 20 будут либо ложно отрицательными, либо ложно положительными.
Стоит обратить внимание на то, что в некоторых задачах необходимо определить всех пациентов с диагнозом и можно даже пренебречь ложно положительными исходами, так как они могут отсеяться на следующих стадиях исследования (например, после контрольной сдачи анализов), тогда необходимо добавить к этой метрике ещё одну, которая могла бы оценить требуемый приоритет.
Precision
Несмотря на различные английские названия и разные формулы подсчета, русский перевод этой метрики также закрепился как «точность», что может вызвать недоумение и конфуз, поэтому следует уточнять, о чем именно вы говорите. Эта точность показывает количество истинно положительных исходов из всего набора положительных меток и считается по следующей формуле [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
Важность этой метрики определяется тем, насколько высока для рассматриваемой задачи «цена» ложно положительного результата. Если, например, стоимость дальнейшей проверки наличия заболевания у пациента высока и мы просто не можем проверить все ложно положительные результаты, то стоит максимизировать данную метрику, ведь при Precision = 50% из 100 положительно определенных больных диагноз будут иметь лишь 50 из них.
Recall (true positive rate)
В русском языке для этого термина используется слово «полнота» или «чувствительность». Эта метрика определяет количество истинно положительных среди всех меток класса, которые были определены как «положительный» и вычисляется по следующей формуле [The relationship between Precision-Recall and ROC curves ].
Необходимо уделить особое внимание этой оценке, когда в поставленной задаче ошибка нераспознания положительного класса высока, например, при выставлении диагноза какой-либо смертельной болезни.
F1-Score
В том случае, если Precision и Recall являются одинаково значимыми, можно использовать их среднее гармоническое для получения оценки результатов [On extending f-measure and g-mean metrics to multi-class problems]:
Помимо точечных оценок, существует целый ряд графических методов, способных оценить качество классификации.
ROC
ROC (receiver operating characteristic) – график, показывающий зависимость верно классифицируемых объектов положительного класса от ложно положительно классифицируемых объектов негативного класса. Иными словами, соотношение True Positive Rate (Recall) и False Positive Rate (Рисунок 2). При этом, False Positive Rate (FPR) рассчитывается по следующей формуле [Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation]:
Рисунок 2: ROC кривая
Рисунок 2 содержит пример двух ROC – кривых. Идеальное значение графика находится в верхней левой точке (TPR = 1, a FPR = 0). При этом, кривая, соответствующая FPR = TPR является случайным гаданием, а если график кривой модели или точка находятся ниже этого минимума, то это говорит лишь о том, что лучше подбрасывать монетку, чем использовать эту модель. При этом говорят, что кривая X доминирует над другой кривой Y, если X в любом точке находится левее и выше Y [Using AUC and accuracy in evaluating learning algorithms ], что означает превосходство первого классификатора над вторым.
С помощью ROC — кривой, можно сравнить модели, а также их параметры для поиска наиболее оптимальной (с точки зрения tpr и fpr) комбинации. В этом случае ищется компромисс между количеством больных, метка которых была правильно определена как положительная и количеством больных, метка которых была неправильно определена как положительная.
AUC (Area Under Curve)
В качестве численной оценки ROC кривой принято брать площадь под этой кривой, которая является неплохим «итогом» для кривой. Если между кривыми X и Y существует доминирование первой над второй, то AUC (X) > AUC (Y), обратное не всегда верно. Но AUC обладает так же и статистическим смыслом: она показывает вероятность того, что случайно выбранный экземпляр негативного класса будет иметь меньше вероятность быть распознанным как позитивный класс, чем случайно выбранный позитивный класс [Using AUC and accuracy in evaluating learning algorithms].
AUC часто сравнивают с метрикой Accuracy и у первой есть явное преимущество при исследовании некоторых моделей — она может работать с вероятностями. Например, в AUC: a better measure than accuracy in comparing learning algorithms показан следующий пример (Рисунок 3): пусть две модели классифицируют 10 тестовых экземпляров. 5 они классифицируют как положительный класс и столько же как отрицательный, так же экземпляры упорядочены в соответствии с вероятностью принадлежать положительному классу (слева — направо). Оба классификатора имеют одинаковую точность — 80%, но AUC у первого — 0.96, а у второго — 0.64, поскольку вероятности ошибочных экземпляров разная. Но так же можно найти и контрпример, когда AUC одинаковый, а точность разная [ AUC: a better measure than accuracy in comparing learning algorithms].
Рисунок 3.Два классификатора имеют одинаковую точность, но разный AUC
Мульти-классификация
Все рассмотренные выше метрики относились лишь к бинарной задаче, но, зачастую, классов больше, чем два. Это обуславливает необходимость в обобщении рассмотренных метрик. Одним из возможных способов является вычисление среднего метрики по всем классам [On extending f-measure and g-mean metrics to multi-class problems]. Тогда в качестве «положительного» класса берется вычисляемый, а все остальные — в качестве «отрицательного».
В этом случае формулы для метрик будут выглядеть следующим образом:
Применение в предиктивной аналитике для здравоохранения
Изученную теорию всегда следует подкрепить практикой. В данном случае, можно рассмотреть применение тех или иных метрик для реальных задач, связанных с использованием моделей машинного обучения в здравоохранении. В большинстве случаев рекомендуется использовать метрики AUC и F-Score, потому что они включают в себя широкий список возможных исходов и, как было замечено ранее, AUC превосходит метрику Accuracy, но спор насчет этого ведётся до сих пор.
Основной задачей предиктивной аналитики для здравоохранения является предсказание различных событий. Эта тема довольно неплохо изучена для различных заболеваний и сценариев использования, поэтому существует множество возможных методов её решения. Данный тип задач оценивается всеми рассмотренными метриками для классификации, но чаще остальных можно заметить Accuracy благодаря её простоте. Например, в Disease prediction by machine learning over big data from healthcare communities авторы анализируют медицинские записи с целью предсказания возможности появления какого-либо заболевания и у них получается это на уровне 70% для Accuracy, Precision, Recall и F1. В Intelligent heart disease prediction system using data mining techniques и Heart disease prediction system using naive Bayes метрика Accuracy достигает приблизительно 90-95%, но на это сказывается размер набора данных, который был использован для исследования.
Среди всего списка заболеваний особую актуальность имеют сердечно сосудистые заболевания (ССЗ). Множество исследований, посвященных предсказанию ССЗ демонстрируют то, чего можно достичь в этой области благодаря машинному обучению. Зачастую здесь используется метрика AUC для сравнения качества моделей. Например в A data-driven approach to predicting diabetes and cardiovascular disease with machine learning авторы работали с базой, которая собиралась в течение 20 лет, содержащей более ста признаков. Целью являлось предсказание ранних стадий ССЗ, предиабета и диабета, они добились показателей равных 0.957, 0.802 и 0.839 площади под кривой. В Development and verification of prediction models for preventing cardiovascular diseases авторы исследовали возможность различных исходов (смерть, госпитализация и другие), связанных с ССЗ. Наилучший показатель AUC был равен 0.96. В Перспективы использования методов машинного обучения для предсказания сердечно-сосудистых заболеваний исследуется возможность предсказания ССЗ с помощью методов машинного обучения и некоторых медицинских данных. Для Accuracy, Precision, Recall и AUC были получены результаты 78%, 0.79, 0.67 и 0.84 соответственно.
Заключение
Рассмотренные метрики являются лишь основными и только для задачи классификации. Существует ещё множество различных областей, в которых они будут разными, потому что каждая задача имеют свою специфику и приоритеты. Невозможно дать каких-то четких гарантий и определить, какая из метрик лучше, выбирать и отдавать предпочтение стоит лишь исходя из опыта своего и других исследователей.
F1 Score против ROC AUC против точности против PR AUC: какую метрику оценки выбрать?
PR AUC и F1 Score — это очень надежные метрики оценки, которые отлично подходят для решения многих задач классификации, но, по моему опыту, чаще всего используются метрики Accuracy и ROC AUC. Они лучше? На самом деле, нет. Как и в случае со знаменитым обсуждением «AUC против точности»: есть реальные преимущества в использовании обоих. Большой вопрос — , когда .
Есть много вопросов, которые могут у вас возникнуть прямо сейчас:
- Когда точность является лучшим показателем оценки, чем ROC AUC?
- Для чего нужен счет F1?
- Что такое кривая PR и как ее использовать?
- Если моя проблема сильно несбалансирована, следует ли мне использовать ROC AUC или PR AUC?
Как всегда, зависит от обстоятельств, но понимание компромиссов между разными показателями имеет решающее значение, когда дело доходит до принятия правильного решения.
В этом сообщении в блоге я буду:
- Поговорите о наиболее распространенных двоичных классификациях метрики , таких как оценка F1, ROC AUC, PR AUC и точность
- Сравните их на примере задачи двоичной классификации
- расскажет вам , что вам следует учитывать при решении выбрать одну метрику вместо другой (оценка F1 против ROC AUC).
Хорошо, давайте сделаем это!
Вы узнаете о:
Обзор показателей оценки
Я начну с представления каждой из этих классификационных метрик.В частности:
- Что такое определение и интуиция за ним,
- Нетехническое объяснение ,
- Как его вычислить или построить ,
- Когда следует использовать .
1. Точность
Он измеряет, сколько наблюдений, как положительных, так и отрицательных, были правильно классифицированы.
Вы не должны использовать точность для несбалансированных проблем .Тогда легко получить высокую оценку точности, просто отнеся все наблюдения к классу большинства.
В Python это можно вычислить следующим образом:
из sklearn.metrics import confusion_matrix, precision_score y_pred_class = y_pred_pos> порог tn, fp, fn, tp = confusion_matrix (y_true, y_pred_class) .ravel () точность = (tp + tn) / (tp + fp + fn + tn) precision_score (y_true, y_pred_class)
Поскольку оценка точности рассчитывается на основе прогнозируемых классов (не оценок прогнозирования), нам необходимо применить определенный порог перед его вычислением.Очевидный выбор — порог 0,5, но он может быть неоптимальным.
Давайте посмотрим на примере , как точность зависит от порога выбор:
Вы можете использовать диаграммы, подобные приведенной выше, для определения оптимального порога. В этом случае выбор чего-то немного выше стандартного 0,5 может немного поднять результат на 0,9686-> 0,9688, но в других случаях улучшение может быть более существенным.
Итак, , когда имеет смысл использовать ?
- Когда ваша проблема сбалансирована, с использованием точности обычно является хорошим началом.Дополнительным преимуществом является то, что это действительно легко объяснить нетехническим заинтересованным сторонам в вашем проекте,
- Когда каждый класс одинаково важен для вас .
2. Оценка F1
Проще говоря, он объединяет точность и отзыв в одну метрику, вычисляя гармоническое среднее между этими двумя. На самом деле это частный случай для , более общая функция F beta :
При выборе бета-версии в вашей оценке F-beta , чем больше вы заботитесь об отзыве , а не точности , тем более высокую бета-версию вам следует выбрать.Например, при оценке F1 мы одинаково заботимся об отзыве и точности, при оценке F2 отзыв для нас в два раза важнее.
При 0
Его можно легко вычислить, запустив:
из sklearn.metrics import f1_score y_pred_class = y_pred_pos> порог f1_score (y_true, y_pred_class)
Важно помнить, что оценка F1 рассчитывается на основе точности и отзыва, которые, в свою очередь, рассчитываются для предсказанных классов (а не оценок предсказания).
Как выбрать оптимальный порог? Построим график оценки F1 для всех возможных пороговых значений:
Мы можем настроить порог, чтобы оптимизировать оценку F1 . Обратите внимание, что и для точности, и для отзыва вы можете получить отличные оценки, увеличивая или уменьшая порог. Хорошо, что вы можете найти золотую середину для оценки F1. Как видите, правильное установление порога действительно может улучшить ваш результат с 0,8077 до 0,8121.
Когда его использовать?
- Практически во всех задачах бинарной классификации, где больше важен положительный класс. Это моя метрика , когда я работаю над этими проблемами.
- Это можно легко объяснить заинтересованным лицам , что во многих случаях может быть решающим фактором. Всегда помните, машинное обучение — это всего лишь инструмент для решения бизнес-задачи.
3. ROC AUC
AUC означает площадь под кривой, поэтому, чтобы говорить о показателе ROC AUC, нам нужно сначала определить кривую ROC.
Это диаграмма, которая визуализирует компромисс между истинно положительной скоростью (TPR) и ложной положительной скоростью (FPR).По сути, для каждого порога мы рассчитываем TPR и FPR и наносим их на один график.
Конечно, чем выше TPR и ниже FPR для каждого порога, тем лучше, и поэтому лучше подходят классификаторы, у которых кривые более левые вверху.
Подробное обсуждение кривой ROC и показателя ROC AUC можно найти в этой статье Тома Фосетта.
Мы можем видеть здоровую кривую ROC, сдвинутую к верхнему левому краю как для положительных, так и для отрицательных классов. Неясно, какой из них работает лучше по всем направлениям, как с FPR <~ 0.15 положительный класс выше, а начиная с FPR ~ 0,15 отрицательный класс выше.
Чтобы получить одно число, которое говорит нам, насколько хороша наша кривая, мы можем вычислить площадь под кривой ROC или показатель ROC AUC. Чем больше верхняя левая кривая, тем выше площадь и, следовательно, выше показатель ROC AUC.
В качестве альтернативы можно показать, что оценка ROC AUC эквивалентна вычислению ранговой корреляции между прогнозами и целями. С точки зрения интерпретации он более полезен, потому что он говорит нам, что этот показатель показывает, насколько хороша в ранжировании прогнозов ваша модель .Он сообщает вам, какова вероятность того, что случайно выбранный положительный экземпляр получит более высокий рейтинг, чем случайно выбранный отрицательный экземпляр.
из sklearn.metrics import roc_auc_score roc_auc = roc_auc_score (y_true, y_pred_pos)
- Вам, , следует использовать его , когда вы в конечном итоге заботитесь о ранжировании прогнозов , а не обязательно о выводе хорошо откалиброванных вероятностей (прочтите эту статью Джейсона Браунли, если вы хотите узнать о калибровке вероятностей).
- не следует использовать , если данные сильно несбалансированы . В этой статье это широко обсуждали Такая Сайто и Марк Ремсмайер. Интуиция такова: количество ложных срабатываний для сильно несбалансированных наборов данных снижается из-за большого количества истинно отрицательных результатов.
- Вы должны использовать его , когда в равной степени заботитесь о положительных и отрицательных классах . Это естественным образом расширяет обсуждение несбалансированных данных из предыдущего раздела.Если мы заботимся об истинных отрицаниях так же, как об истинных положительных моментах, тогда имеет смысл использовать ROC AUC.
4. PR AUC | Средняя точность
Аналогично ROC AUC, чтобы определить PR AUC, нам нужно определить, какая кривая Precision -Recall.
Это кривая, сочетающая точность (PPV) и отзыв (TPR) в одной визуализации. Для каждого порога вы рассчитываете PPV и TPR и наносите его на график. Чем выше по оси Y ваша кривая, тем лучше производительность вашей модели.
Вы можете использовать этот график, чтобы принять обоснованное решение, когда дело доходит до классической дилеммы точности / отзыва. Очевидно, что чем выше отзыв, тем ниже точность. Зная , при котором ваша точность начинает быстро падать, может помочь вам выбрать порог и создать лучшую модель.
Мы видим, что для отрицательного класса мы поддерживаем высокую точность и высокую полноту почти во всем диапазоне пороговых значений. Для положительного класса точность начинает падать, как только мы вспоминаем 0.2 истинных положительных результатов, и к тому времени, когда мы достигнем 0,8, оно снизится до 0,7.
Аналогично показателю ROC AUC вы можете рассчитать площадь под кривой точности-отзыва, чтобы получить одно число, которое описывает производительность модели.
Можно также представить PR AUC как среднее значение оценок точности, рассчитанных для каждого порога отзыва . Вы также можете настроить это определение в соответствии с потребностями вашего бизнеса, выбрав / обрезав пороговые значения отзыва при необходимости.
из sklearn.импорт показателей average_precision_score average_precision_score (y_true, y_pred_pos)
- , если вы хотите сообщить о решении о точности / отзыве другим заинтересованным сторонам
- , если вы хотите выбрать порог, который соответствует бизнес-задаче .
- , когда ваши данные сильно несбалансированы . Как упоминалось ранее, в этой статье это подробно обсуждали Такая Сайто и Марк Ремсмайер. Интуиция такова: поскольку PR AUC фокусируется в основном на положительном классе (PPV и TPR), его меньше волнует частый отрицательный класс.
- когда вас больше волнует положительный, чем отрицательный класс . Если вас больше интересует положительный класс и, следовательно, PPV и TPR, вам следует использовать кривую Precision-Recall и PR AUC (средняя точность).
Сравнение оценочных показателей
Мы сравним эти показатели с реальным вариантом использования. На основе недавнего конкурса kaggle я создал пример проблемы обнаружения мошенничества:
- Я выбрал только 43 объекта
- Я взял 66000 наблюдений из исходного набора данных
- Я скорректировал долю положительного класса до 0.09
- Я обучил кучу классификаторов lightGBM с разными гиперпараметрами.
Я хотел иметь интуитивное представление о том, какие модели «действительно» лучше. В частности, я подозреваю, что модель только с 10 деревьями хуже модели со 100 деревьями. Конечно, с большим количеством деревьев и меньшей скоростью обучения становится сложно, но я думаю, что это достойный прокси.
Итак, для комбинаций Learning_rate и n_estimators я сделал следующее:
- определенных значений гиперпараметров:
MODEL_PARAMS = {'random_state': 1234,
'learning_rate': 0.1,
'n_estimators': 10} Модель
= lightgbm.LGBMClassifier (** MODEL_PARAMS) model.fit (X_train, y_train)
y_test_pred = model.predict_proba (X_test)
- зарегистрировал все метрики для каждого запуска:
y_test_pred = model.predict_proba (X_test)
Для получения полной базы кода перейдите в этот репозиторий или изучите код для каждого эксперимента.
Вы также можете перейти сюда и изучить эксперименты с:
- оценочных показателей
- графиков производительности
- показателей по графикам пороговых значений
Давайте посмотрим, как наши модели оцениваются по различным показателям.
По этой проблеме все эти метрики ранжируют модели от лучших к худшим очень схожим образом, но есть небольшие различия. Также сами оценки могут сильно отличаться.
В следующих разделах мы обсудим это более подробно.
5. Точность по сравнению с ROC AUC
Первое большое отличие состоит в том, что вы вычисляете точность для предсказанных классов , а вы вычисляете ROC AUC для предсказанных оценок . Это означает, что вам нужно будет найти оптимальный порог для вашей проблемы.
Кроме того, точность смотрит на доли правильно назначенных положительных и отрицательных классов. Это означает, что если наша задача сильно несбалансирована , мы получим действительно высокую оценку , просто предсказав, что все наблюдения принадлежат классу большинства.
С другой стороны, если ваша проблема сбалансирована , и вы заботитесь как о положительных, так и отрицательных прогнозах , точность — хороший выбор , потому что это действительно просто и легко интерпретировать.
Еще нужно помнить, что ROC AUC особенно хорош для ранжирования прогнозов . Из-за этого, если у вас есть проблема, когда сортировка ваших наблюдений — это то, что вам нужно, ROC, AUC, вероятно, то, что вы ищете.
А теперь посмотрим на результаты наших экспериментов:
Эксперименты, отсортированные по шкале ROC AUC
Первое наблюдение заключается в том, что модели имеют почти одинаковый рейтинг по ROC AUC и точности.
Во-вторых, оценка точности начинается с 0.93 для самой худшей модели и до 0,97 для лучшей. Помните, что прогнозирование всех наблюдений как класс большинства 0 даст точность 0,9, поэтому наш худший эксперимент BIN-98 лишь немного лучше этого. Тем не менее, сама оценка довольно высока, и это показывает, что вы всегда должны учитывать дисбаланс, глядя на точность.
Примечание:
Существует интересная метрика под названием Cohen Kappa, которая учитывает дисбаланс, вычисляя улучшение точности по сравнению с моделью «выборка в соответствии с классовым дисбалансом».
Подробнее о Коэне Каппе здесь.
6. Оценка F1 vs Точность
Обе эти метрики принимают прогнозы класса в качестве входных данных, поэтому вам придется корректировать порог независимо от того, какой из них вы выберете.
Помните, что F1 оценка балансирует точность и отзыв на положительном классе , тогда как точность рассматривает правильно классифицированные наблюдения как положительные, так и отрицательные .Это делает большой разницей , особенно для несбалансированных проблем , где по умолчанию наша модель будет хорошо предсказывать истинные отрицания и, следовательно, точность будет высокой. Однако, если вы одинаково заботитесь об истинных отрицаниях и истинных положительных результатах, тогда вам следует выбрать точность.
Если мы посмотрим на наши эксперименты ниже:
Эксперименты, отсортированные по баллу F1
В нашем примере обе метрики в равной степени могут помочь нам ранжировать модели и выбирать лучшую.Дисбаланс класса из 1-10 делает нашу точность действительно высокой по умолчанию. Из-за этого даже наихудшая модель имеет очень высокую точность, и улучшения, которые мы продвигаемся к началу таблицы, не так очевидны в отношении точности, как в оценке F1.
7. ROC AUC и PR AUC
Общим между ROC AUC и PR AUC является то, что они оба смотрят на оценки прогнозирования моделей классификации, а не на присвоения классов с использованием пороговых значений. Отличие, однако, заключается в том, что ROC AUC смотрит на как истинно положительный показатель TPR и ложноположительный показатель FPR , в то время как PR AUC смотрит на положительное прогнозное значение PPV и истинное положительное значение TPR .
Из-за этого , если вы больше заботитесь о положительном классе, то лучше использовать PR AUC , который более чувствителен к улучшениям для положительного класса. Один из распространенных сценариев — это сильно несбалансированный набор данных, где доля положительного класса, которую мы хотим найти (как при обнаружении мошенничества), мала. Я настоятельно рекомендую взглянуть на это ядро kaggle для более подробного обсуждения темы ROC AUC и PR AUC для несбалансированных наборов данных.
Если вы одинаково заботитесь о положительном и отрицательном классе или ваш набор данных достаточно сбалансирован, то использование ROC AUC — хорошая идея.
Давайте сравним наши эксперименты по этим двум показателям:
Эксперименты, отсортированные по шкале ROC AUC
Они ранжируют модели аналогично, но есть небольшая разница, если вы посмотрите на эксперименты BIN-100 и BIN 102.
Однако улучшения, рассчитанные с помощью средней точности (PR AUC), больше и яснее. Мы получаем от 0,69 до 0,87, когда в то же время ROC AUC изменяется с 0,92 до 0,97. Из-за этого ROC AUC может дать ложное представление об очень высокой производительности , хотя на самом деле ваша модель может работать не так хорошо.
8. Оценка F1 против ROC AUC
Одно большое различие между оценкой F1 и ROC AUC заключается в том, что первый принимает предсказанные классы, а второй — предсказанные оценки в качестве входных данных. Из-за этого с оценкой F1 вам нужно выбрать порог , который присваивает ваши наблюдения этим классам. Часто вы можете значительно улучшить производительность своей модели, если вы правильно ее выберете.
Итак, , если вас интересуют прогнозы ранжирования , не нужно, чтобы они были правильно откалиброваны вероятностями, и ваш набор данных не сильно разбалансирован , тогда я бы выбрал ROC AUC .
Если ваш набор данных сильно несбалансирован и / или вас больше волнует положительный класс, я бы подумал об использовании балла F1 или кривой Precision-Recall и PR AUC . Дополнительная причина использовать F1 (или Fbeta) состоит в том, что эти метрики легче интерпретировать и передавать заинтересованным сторонам бизнеса.
Давайте взглянем на результаты экспериментов, чтобы узнать больше:
Эксперименты, отсортированные по баллу F1
Эксперименты оцениваются одинаково по шкале F1 (порог = 0.5 ) и ROC AUC. Однако оценка F1 ниже по значению, а разница между худшей и лучшей моделью больше. Для показателя ROC AUC значения больше, а разница меньше. Особенно интересен эксперимент BIN-98, который имеет показатель F1 0,45 и ROC AUC 0,92. Причина в том, что порог 0,5 — действительно плохой выбор для модели, которая еще не обучена (всего 10 деревьев). Вы можете получить оценку F1 0,63, если установите ее на 0,24, как показано ниже:
Примечание:
Если вы хотите легко регистрировать эти графики для каждого эксперимента, я прикрепляю помощника по ведению журнала в конце этого сообщения.
Заключительные мысли
В этом сообщении блога вы узнали о , о , , о нескольких общих метриках , используемых для оценки моделей двоичной классификации.
Мы обсудили, как они определяются, как их интерпретировать и вычислять, и когда вам следует подумать об их использовании.
Наконец, , мы сравнили эти оценочные показатели с реальной проблемой и обсудили некоторые типичные решения, с которыми вы можете столкнуться.
Обладая всеми этими знаниями, у вас есть оборудование, чтобы выбрать хорошую метрику оценки для вашей следующей задачи двоичной классификации!
Бонус:
Чтобы упростить задачу, я приготовил:
Посмотрите на них ниже!
Вспомогательная функция ведения журнала
Если вы хотите, чтобы регистрировал все из этих показателей и производительности диаграмм , которые мы рассмотрели для вашего проекта машинного обучения , с помощью всего одного вызова функции и исследуйте их в Нептуне.
pip install neptune-contrib [все]
импортировать neptunecontrib.monitoring.metrics как npt_metrics npt_metrics.log_binary_classification_metrics (y_true, y_pred)
- узнайте все в приложении:
Шпаргалка по метрикам двоичной классификации
Мы создали для вас прекрасную шпаргалку, которая включает весь контент, который я просмотрел в этом сообщении в блоге, и помещает его на несколько страниц, удобоваримый документ, который вы можете распечатать и использовать всякий раз, когда вам нужны какие-либо показатели двоичной классификации.
Получите шпаргалку с метриками двоичной классификации.
Скачать
Старший специалист по данным
Вам понравилось? Поделитесь этим и позвольте другим наслаждаться этим!
Получайте уведомления о новых статьях
Отправляя форму, вы даете сконцентрироваться на хранении предоставленной информации и на связи с вами.
Пожалуйста, ознакомьтесь с нашей Политикой конфиденциальности для получения дополнительной информации.
Другие статьи, которые вы можете прочитать
sklearn 计算 ROC 曲线 下 面积 AUC — 简 书
sklearn.metrics.auc (x, y, reorder = False)
通用 方法 , 使用 梯形 规则 计算 曲线 下 面积。
импортировать numpy как np
из показателей импорта sklearn
y = np.array ([1, 1, 2, 2])
pred = np.array ([0,1, 0,4, 0,35, 0,8])
fpr, tpr, thresholds = metrics.roc_curve (y, pred, pos_label = 2)
metrics.auc (fpr, tpr)
sklearn.metrics.roc_auc_score (y_true, y_score, average = ‘macro’, sample_weight = None)
得分 曲线 下 的 面积。
只 用 在 二 分类 индикатор этикетки 格式 的 多 分类。
- y_true: array, shape = [n_samples] или [n_samples, n_classes]
真实 的 标签 - y_score: array, shape = [n_samples] или [n_samples, n_classes]
预测 得分 , 类 的 估计 概率 、 置信 值 分类 «solution_function» 的 返回 值 ; - среднее: строка, [Нет, «микро», «макрос» (по умолчанию), «образцы», «взвешенный»]
- sample_weight: подобный массиву shape = [n_samples], необязательно
импортировать numpy как np
из склеарна.импорт показателей roc_auc_score
y_true = np.array ([0, 0, 1, 1])
y_scores = np.array ([0,1, 0,4, 0,35, 0,8])
roc_auc_score (y_true, y_scores)
из sklearn import datasets, svm, metrics, model_selection, preprocessing
iris = datasets.load_iris ()
x = iris.data [iris.target! = 0,: 2]
x = предварительная обработка.StandardScaler (). fit_transform (x)
y = iris.target [iris.target! = 0]
x_train, x_test, y_train, y_test = model_selection.train_test_split (x, y,
test_size = 0,1, random_state = 25)
clf = svm.SVC (ядро = 'линейный')
clf.подходят (x_train, y_train)
metrics.f1_score (y_test, clf.predict (x_test))
0,75
fpr, tpr, thresholds = metrics.roc_curve (y_test, clf.decision_function (x_test),
pos_label = 2)
metrics.auc (fpr, tpr)
0,95833333333333337
roc_auc_score 预测 得分 曲线 下 的 auc , 在 计算 的 时候 调用 了 auc ;
def _binary_roc_auc_score (y_true, y_score, sample_weight = None):
если len (np.unique (y_true))! = 2:
Raise ValueError ("Только один класс присутствует в y_true. ROC AUC score"
"не определяется в этом случае.")
fpr, tpr, tresholds = roc_curve (y_true, y_score,
sample_weight = sample_weight)
return auc (fpr, tpr, reorder = True)
两种 方法 都 可以 得到 同样 的 结果。
импортировать numpy как np
из sklearn.metrics import roc_auc_score
y_true = np.array ([0, 0, 1, 1])
y_scores = np.array ([0,1, 0,4, 0,35, 0,8])
печать (roc_auc_score (y_true, y_scores))
0,75
fpr, tpr, thresholds = metrics.roc_curve (y_true, y_scores, pos_label = 1)
печать (metrics.auc (fpr, tpr))
0.75
的 是 roc_auc_score 中 不能 设置 pos_label , 而 在 roc_curve 中 , pos_label 的 默认 设置 如下 :
классы = np.unique (y_true)
if (pos_label равно None и
not (array_equal (classes, [0, 1]) или
array_equal (классы, [-1, 1]) или
array_equal (классы, [0]) или
array_equal (классы, [-1]) или
array_equal (классы, [1]))):
поднять ValueError ("Данные не являются двоичными и pos_label не указан")
elif pos_label равно None:
pos_label = 1. roc_auc_score 中 pos_label 必须 满足 以
sklearn : auc 、 roc_curve 、 roc_auc_score_NockinOnHeavensDoor 的 博客 -CSDN 000
sklearn.metrics.auc
作用 : 计算 AUC (Площадь под кривой)
metrics.roc_curve
作用 : 计算 ROC (рабочая характеристика приемника)
注意: эта реализация ограничена задачей двоичной классификации
sklearn.metrics.roc_curve (y_true, y_score, pos_label = None, sample_weight = None, drop_intermediate = True)
параметр:
y_true: массив, shape = [n_samples] Истинные двоичные метки. Если метки не являются ни {-1, 1}, ни {0, 1}, то pos_label должен быть явно заданy_score: array, shape = [n_samples]pos_label:int или str, по умолчанию = None, Метка считается положительной, а остальные считаются отрицательными.
Возврат
-
fpr: количество ложных срабатываний -
tpr: истинно положительное значение -
пороговые значения: массив, форма = [n_thresholds]
例子 :
-
pos_label = 1即 表示 标签 为 1 的 是 正 样本 , 其余 的 都是 负 样本 , 因为 这个 只能 做 二 分类
import numpy as np
из показателей импорта sklearn
y = np.массив ([1, 1, 2, 2,3,3])
pred = np.array ([0,1, 0,4, 0,35, 0,8,0,1,0,8])
fpr, tpr, thresholds = metrics.roc_curve (y, pred, pos_label = 1)
metrics.auc (fpr, tpr)
0,3125
sklearn.metrics.roc_auc_score
作用 : Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) на основе оценок прогноза
注意 : Эта реализация ограничена задачей двоичной классификации или задачей классификации с несколькими метками в формате индикатора метки.
sklearn.metrics.roc_auc_score (y_true, y_score, average = ’macro’, sample_weight = None, max_fpr = None)
Параметры:
y_true : массив, shape = [n_samples] или [n_samples, n_classes]
y_score : массив, shape = [n_samples] или [n_samples, n_classes]
средний : строка, [None, ‘micro’, ‘macro’ (по умолчанию), ‘samples’, ‘weighted’] , Если нет, возвращаются баллы для каждого класса. В противном случае это определяет тип усреднения, выполняемого для данных。
Возвраты:
auc : поплавок
### roc_auc_score
импортировать numpy как np
из склеарна.импорт показателей roc_auc_score
y_true = np.array ([0, 0, 1, 1])
y_scores = np.array ([0,1, 0,4, 0,35, 0,8])
roc_auc_score (y_true, y_scores)
0,75
roc_auc_score 是 预测 得分 曲线 下 的 auc , 在 计算 的 时候 调用 了 auc ;
def _binary_roc_auc_score (y_true, y_score, sample_weight = None):
если len (np.unique (y_true))! = 2:
Raise ValueError ("Только один класс присутствует в y_true. ROC AUC score"
"не определено в этом случае.")
fpr, tpr, tresholds = roc_curve (y_true, y_score,
sample_weight = sample_weight)
return auc (fpr, tpr, reorder = True)
所以 不能 用 在 多 分类 问题 上。
多 分类 问题 的 auc 计算 例子 :
импортировать numpy как np
импортировать matplotlib.pyplot как plt
из цикла импорта itertools
из sklearn import svm, datasets
из sklearn.metrics import roc_curve, auc
из sklearn.model_selection import train_test_split
из sklearn.preprocessing import label_binarize
из sklearn.multiclass import OneVsRestClassifier
из scipy import interp
导入 数据 :
iris = datasets.load_iris ()
X = iris.data
y = iris.target
对 训练 标签 做 标签 二 值 化 运算 (одноразовое 编码) :
# Бинаризация вывода
y = label_binarize (y, classes = [0,1,2])
n_classes = y.форма [1]
n_classes
3
对 每个 数据 在 尾部 加入 噪音 :
# Добавьте шумные функции, чтобы усложнить проблему
random_state = np.random.RandomState (0)
n_samples, n_features = X.shape
X = np.c_ [X, random_state.randn (n_samples, 200 * n_features)]
注 : np.c_
np.c_ [random_state.randn (2,2), [[0,0], [1,1]]]
массив ([[0,73381936, 0,267, 0., 0.],
[1.07274021, -0.9826661, 1., 1.]])
划分 数据 集 :
# случайные и сплит обучающие и тестовые наборы
X_train, X_test, y_train, y_test = train_test_split (X, y, test_size =.5, random_state = 0)
подходит 一个 分类 器 :
# Научитесь предсказывать каждый класс по сравнению с другим
classifier = OneVsRestClassifier (svm.SVC (ядро = 'linear', вероятность = True,
random_state = random_state))
y_score = classifier.fit (X_train, y_train) .decision_function (X_test)
注 : solution_function (X) :
Возвращает расстояние каждой выборки от границы решения для каждого класса.
每 一个 类别 的 ROC 与 AUC :
# Вычислить кривую ROC и область ROC для каждого класса
fpr = dict ()
tpr = dict ()
roc_auc = dict ()
для i в диапазоне (n_classes):
# 取 出来 的 是 各个 类 的 测试 值 和 预测 值
fpr [i], tpr [i], _ = roc_curve (y_test [:, i], y_score [:, i])
roc_auc [i] = auc (fpr [i], tpr [i])
# Вычислить микросреднюю кривую ROC и площадь ROC
# 总和 的 基础 上 平均 的 ROC 和 AUC
fpr ["micro"], tpr ["micro"], _ = roc_curve (y_test.ravel (), y_score.ravel ())
roc_auc ["micro"] = auc (fpr ["micro"], tpr ["micro"])
绘图
plt.rcParams ['savefig.dpi'] = 300 # 图片 像素
plt.rcParams ['figure.dpi'] = 300 # 分辨率
plt.figure ()
# ширина линии
lw = 2
plt.plot (fpr [2], tpr [2], color = 'darkorange',
lw = lw, label = 'Кривая ROC (площадь =% 0,2f)'% roc_auc [2])
plt.plot ([0, 1], [0, 1], color = 'navy', lw = lw, linestyle = '-')
plt.xlim ([0.0, 1.0])
plt.ylim ([0.0, 1.05])
plt.xlabel ('ложноположительная ставка')
plt.ylabel ('Истинно положительная оценка')
plt.title ('Пример рабочей характеристики приемника')
plt.legend (loc = "нижний правый")
plt.show ()
# Вычислить макросреднюю кривую ROC и площадь ROC
# Сначала суммируем все ложные срабатывания
all_fpr = np.unique (np.concatenate ([fpr [i] для i в диапазоне (n_classes)]))
# Затем интерполируем все кривые ROC в этих точках
mean_tpr = np.zeros_like (all_fpr)
для i в диапазоне (n_classes):
mean_tpr + = interp (all_fpr, fpr [i], tpr [i])
# Наконец усредните и вычислите AUC
mean_tpr / = n_classes
fpr ["макрос"] = all_fpr
tpr ["макрос"] = mean_tpr
roc_auc ["макрос"] = auc (fpr ["макрос"], tpr ["макрос"])
# Постройте все кривые ROC
plt.рисунок ()
plt.plot (fpr ["микро"], tpr ["микро"],
label = 'микросредняя кривая ROC (площадь = {0: 0,2f})'
'' .format (roc_auc ["micro"]),
цвет = 'deeppink', linestyle = ':', linewidth = 4)
plt.plot (fpr ["макрос"], tpr ["макрос"],
label = 'макро-средняя кривая ROC (площадь = {0: 0,2f})'
'' .format (roc_auc ["макрос"]),
цвет = 'темно-синий', стиль линии = ':', ширина линии = 4)
цвета = цикл (['голубой', 'темно-оранжевый', 'васильковый'])
для i, цвет в zip (диапазон (n_classes), цветов):
plt.сюжет (fpr [i], tpr [i], color = color, lw = lw,
label = 'Кривая ROC класса {0} (площадь = {1: 0.2f})'
'' .format (i, roc_auc [i]))
plt.plot ([0, 1], [0, 1], 'k--', lw = lw)
plt.xlim ([0.0, 1.0])
plt.ylim ([0.0, 1.05])
plt.xlabel ('ложноположительная ставка')
plt.ylabel ('Истинно положительная оценка')
plt.title ('Некоторое расширение рабочих характеристик приемника до мультикласса')
plt.legend (loc = "нижний правый")
plt.show ()
Рисование кривой ROC — OpenEye Python Cookbook vOct 2019
Проблема
Вы хотите нарисовать кривую ROC , чтобы визуализировать производительность
метод бинарной классификации (см. Рисунок 1 ).
Рисунок 1. Пример кривых ROC
Решение
Двоичная классификация — это задача классификации членов данного набора
объекты на две группы в зависимости от того, имеют они какое-либо свойство или нет.
Есть четыре возможных результата бинарного классификатора
(см. Рисунок 2 ):
- истинное положительное (TP) : прогнозируемое положительное значение, фактическое значение также положительное
- ложное срабатывание (FP) : прогноз положительный, но фактическое значение отрицательное
- истинно отрицательное (TN) : прогнозируемое отрицательное значение, фактическое значение также отрицательное
- ложноотрицательный (FN) : прогнозируемое отрицательное значение, но фактическое значение положительное
При моделировании молекул положительные объекты обычно называют активными , а отрицательные
одни называются приманками .
Рисунок 2. Матрица неточностей
Из приведенных выше чисел можно рассчитать следующее:
- истинно положительных результатов: \ (TPR = \ frac {положительные результаты \ правильно \ классифицированы} {total \ positives} = \ frac {TP} {P} \)
- количество ложных срабатываний: \ (FPR = \ frac {negatives \ неправильно \ классифицировано} {total \ negatives} = \ frac {FP} {N} \)
Кривая рабочей характеристики приемника (ROC) представляет собой два
размерный график, на котором нанесено ложных срабатываний
ось X и истинно положительный коэффициент отложен по оси Y.В
Кривые ROC полезны для визуализации и сравнения производительности
методы классификатора (см. Рисунок 1 ).
На рисунке 3 показана кривая ROC для примера испытательного набора.
из 18 объектов (7 активных, 11 ложных целей), которые показаны в таблице 1
в порядке возрастания их оценок.
Для небольшого набора тестов кривая ROC на самом деле является ступенчатой функцией: активный объект в
Стол 1 перемещает линию вверх, а ловушка перемещает ее
направо.
Таблица 1.Пример данных для ROC id балл активный / ложный id балл активный / ложный O 0,03 a L 0,48 a Дж 0,08 a К 0,56 д Д 0.10 д P 0,65 д А 0,11 a Q 0,71 д я 0,22 д С 0,72 д G 0,32 a N 0,73 a B 0,35 a H 0.80 д M 0,42 д R 0,82 д Ф 0,44 д E 0,99 д
Рисунок 3. Пример кривой ROC
В следующем фрагменте кода показано, как вычислить истинно положительных и ложных положительных
ставки для графика Рисунок 3 .Функция get_rates , которая принимает следующие параметры:
- актив
- Список идентификаторов активов.
В нашем простом примере с таблицей 1 активными являются: [«A», «B», «G», «J», «L», «N», «O»] - баллов
- Список кортежей (id, score) в порядке возрастания оценок.
Он генерирует значения tpt и fpt , т.е. увеличивающиеся истинные положительные значения
и положительные ставки соответственно.В качестве альтернативы можно рассчитать значения tpt и fpt
с помощью функции sklearn.metrics.roc_curve ().
См. Пример в Построение ROC-кривых сходства отпечатков пальцев .
Примечание
В этом простом примере оценки находятся в диапазоне [0,0, 1,0],
где чем меньше балл, тем лучше.
Для другого диапазона оценок функции должны быть соответственно изменены.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 год
22
23
24
def get_rates (активные, очки):
"" "
: тип активные: список [жало]
: type scores: list [кортеж (строка, число с плавающей точкой)]
: rtype: tuple (список [число], список [число])
"" "
tpr = [0.0] # истинно положительный результат
fpr = [0.0] # количество ложных срабатываний
nractives = len (активные вещества)
nrdecoys = len (баллы) - len (активы)
foundactives = 0,0
founddecoys = 0,0
для idx, (id, score) in enumerate (scores):
если id в активах:
foundactives + = 1.0
еще:
founddecoys + = 1.0
tpr.append (foundactives / float (nractives))
fpr.append (founddecoys / float (nrdecoys))
возврат tpr, fpr
Следующие фрагменты кода показывают, как изображение кривой ROC
( Рисунок 3 ) создается из
истинно положительный и ложноположительный частоты, рассчитанные
get_rates функция.
def depict_ROC_curve (активные, оценки, метка, цвет, имя файла, случайная строка = True):
"" "
: тип активные: список [жало]
: type scores: list [кортеж (строка, число с плавающей точкой)]
: type color: string (шестнадцатеричный код цвета)
: type fname: string
: type randomline: boolean
"" "
plt.figure (figsize = (4, 4), dpi = 80)
setup_ROC_curve_plot (plt)
add_ROC_curve (таблица, актив, оценка, цвет, метка)
save_ROC_curve_plot (plt, имя файла, случайная строка)
def setup_ROC_curve_plot (plt):
"" "
: введите plt: matplotlib.пиплот
"" "
plt.xlabel ("FPR", fontsize = 14)
plt.ylabel ("TPR", fontsize = 14)
plt.title ("Кривая ROC", fontsize = 14)
Также вычисляется номер AUC кривой ROC
(с использованием sklearn.metrics.auc ()) и показано в легенде.
Площадь под кривой (AUC) кривой ROC является совокупным показателем.
производительности по всем возможным порогам классификации.
Диапазон значений: \ ([0.0, 1.0] \).
Модель с идеальными прогнозами имеет AUC, равную 1,0, в то время как модель
который всегда дает неверные прогнозы, имеет значение AUC 0.0.
def add_ROC_curve (plt, активные, очки, цвет, метка):
"" "
: введите plt: matplotlib.pyplot
: тип активные: список [жало]
: type scores: list [кортеж (строка, число с плавающей точкой)]
: type color: string (шестнадцатеричный код цвета)
: метка типа: строка
"" "
tpr, fpr = get_rates (активные, баллы)
roc_auc = auc (fpr, tpr)
roc_label = '{} (AUC = {:. 3f})'. format (label, roc_auc)
plt.plot (fpr, tpr, color = color, linewidth = 2, label = roc_label)
def save_ROC_curve_plot (plt, filename, randomline = True):
"" "
: введите plt: matplotlib.пиплот
: type fname: string
: type randomline: boolean
"" "
если случайная строка:
х = [0,0, 1,0]
plt.plot (x, x, linestyle = 'dashed', color = 'red', linewidth = 2, label = 'random')
plt.xlim (0,0, 1,0)
plt.ylim (0,0, 1,0)
plt.legend (размер шрифта = 10, loc = 'лучший')
plt.tight_layout ()
plt.savefig (имя файла)
Обсуждение
Изображение кривых ROC — хороший способ визуализировать и сравнить
выполнение различных типов отпечатков пальцев.
Молекула, изображенная слева в , Таблица 2, — случайная
молекула, выбранная из набора TXA2 (49 структур) набора данных Briem-Lessel .График справа создан путем выполнения двумерных поисков сходства молекул с использованием четырех из
типы отпечатков пальцев GraphSim TK (путь, цикл, дерево и ключ MACCS).
Набор приманок — это четыре других класса активности в наборе данных (5HT3, ACE, PAF и HMG-CoA).
вместе с неактивным набором случайно выбранных соединений из MDDR, о принадлежности которых не известно
на любой из пяти занятий.
Таблица 2: Пример кривых ROC для поиска по отпечаткам пальцев с различными типами запрос Кривые ROC
sklearn roc_auc_score 源码 解读 — 知 乎
在 sklearn 中 使用 roc_auc_score () 函数 计算 auc , 其 计算 方式 和 tf.metrics.auc () 计算 方式 基本 一致 , 也是 通过 思想 , 计算 roc 曲线 下 面积 的 小 梯形 之 和 得到 auc 的。 二者 主要 区别 计算 小 梯形 面积 (计算 小 梯形 面积 需要 设置 tp , tn, fp, fn , 进而 计算 tpr, fpr 和 小 梯形 面积)。 第一 , 在 tf.metrics.auc () 中 可以 指定 阈 值 个数 是 是 200 个 阈 值 , 一般 设置 阈 值为 размер пакета 比较。 而 sklearn 的 roc_auc_score () 函数 实现 中 , 直接 指定 了 阈 值 个数 batch size。 第二 , 阈 值 的 产生 也 不同 。tf.metrics.auc () 是 等距 阈 值直接 以 预测 概率 баллов 为 阈 值。
首先 看 roc_auc_score 函数 定义 :
def roc_auc_score (y_true, y_score, average = "macro", sample_weight = None):
"" "Расчетная область под кривой рабочих характеристик приемника (ROC AUC)
Примеры
--------
>>> импортировать numpy как np
>>> из склеарн.импорт показателей roc_auc_score
>>> y_true = np.array ([0, 0, 1, 1])
>>> y_scores = np.array ([0,1, 0,4, 0,35, 0,8])
>>> roc_auc_score (y_true, y_scores)
0,75
"" "
def _binary_roc_auc_score (y_true, y_score, sample_weight = None):
если len (np.unique (y_true))! = 2:
Raise ValueError ("Только один класс присутствует в y_true. ROC AUC score"
"не определено в этом случае.")
fpr, tpr, tresholds = roc_curve (y_true, y_score,
sample_weight = sample_weight)
return auc (fpr, tpr, reorder = True)
вернуть _average_binary_score (
_binary_roc_auc_score, y_true, y_score, средний,
sample_weight = sample_weight)
可以 看到 , 主要 有 两个 , y_true 和 y_score。22 行 的 _average_binary_score 函数 实际上 调用 了 _binary_roc_auc_score (y_true, y_score)调用 roc_curve () 计算 了 fpr, tpr , 然后 调用 auc (fpr, tpr, reorder = True) 得到 auc 值 。auc () 函数 的 实现 和 tf.metrics.auc () 的 实现 基本 一致 , 不再 累。 这里 重点 看下 如何 产生 fpr, tpr 的。
roc_curve () 定义 如下 :
def roc_curve (y_true, y_scoreweight, pos_label = N, sample_label Никто,
drop_intermediate = True):
"" "Рабочая характеристика вычислительного приемника (ROC)
"" "
fps, tps, thresholds = _binary_clf_curve (
y_true, y_score, pos_label = pos_label, sample_weight = sample_weight)
если drop_intermediate и len (fps)> 2:
optim_idxs = np.where (np.r_ [Верно,
нп.логический_или (np.diff (кадр / с, 2),
np.diff (tps, 2)),
Верно]) [0]
fps = fps [оптимальный_idxs]
tps = tps [оптимальный_idxs]
пороги = пороги [optim_idxs]
если tps.size == 0 или fps [0]! = 0:
# При необходимости добавить дополнительную позицию порога
tps = np.r_ [0, tps]
fps = np.r_ [0, fps]
пороги = np.r_ [пороги [0] + 1, пороги]
если fps [-1] <= 0:
предупреждения.warn ("Нет отрицательных образцов в y_true,"
"ложноположительное значение не должно иметь смысла",
UndefinedMetricWarning)
fpr = np.repeat (np.nan, fps.shape)
еще:
fpr = fps / fps [-1]
если tps [-1] <= 0:
warnings.warn ("Нет положительных образцов в y_true,"
"истинно положительное значение не должно иметь смысла",
UndefinedMetricWarning)
tpr = np.repeat (np.nan, tps.shape)
еще:
tpr = tps / tps [-1]
return fpr, tpr, thresholds
roc_curve 函数 的 核心 在 5-6 行 , 如何 计算 tp, fp。 当 知道 tp, fp 之后 , tpr, fpr 就好 计算 了 , 因为 tn, fp 只要 知道 labels 就 可以 计算。 这里 先 说 结论 , 第 5-6 fps, tps 分别 表示 阈 值 下 , fp 和 tp 的 值 , 它们 是 array。
再看 _binary_clf_curve。
def _binary , pos_label = None, sample_weight = None):
"" "Вычислить истинные и ложные срабатывания по порогу двоичной классификации."" "
# Убедитесь, что y_true действителен
y_type = type_of_target (y_true)
если нет (y_type == "двоичный" или
(y_type == "multiclass" и pos_label не равно None)):
поднять ValueError ("Формат {0} не поддерживается" .format (y_type))
check_consistent_length (y_true, y_score, sample_weight)
y_true = column_or_1d (y_true) # column_or_1d 校验 维度
y_score = column_or_1d (y_score)
assert_all_finite (y_true)
assert_all_finite (y_score)
если sample_weight не равно None:
sample_weight = column_or_1d (sample_weight)
# обеспечить двоичную классификацию, если pos_label не указан
классы = np.уникальный (y_true)
if (pos_label равно None и
not (np.array_equal (классы, [0, 1]) или
np.array_equal (классы, [-1, 1]) или
np.array_equal (классы, [0]) или
np.array_equal (классы, [-1]) или
np.array_equal (классы, [1]))):
поднять ValueError ("Данные не являются двоичными и pos_label не указан")
elif pos_label равно None:
pos_label = 1.
# сделать y_true логическим вектором
y_true = (y_true == pos_label)
# сортировать оценки и соответствующие значения истинности
desc_score_indices = нп.argsort (y_score, kind = "mergesort") [:: - 1] #argsort 升序 排序 得到 索引, [:: - 1] 是 反转 功能 , 这里 就是 降序
y_score = y_score [desc_score_indices]
y_true = y_true [desc_score_indices]
если sample_weight не равно None:
weight = sample_weight [desc_score_indices]
еще:
вес = 1.
# y_score обычно имеет много связанных значений. Здесь мы извлекаем
# индексы, связанные с отдельными значениями. Мы также
# объединить значение для конца кривой.
отличное_значение_индексов = np.where (np.diff (y_score)) [0]
threshold_idxs = np.r_ [разные_значения_индексов, y_true.size - 1] # np.r_ 按 列 concat
# накапливаем истинные положительные результаты с уменьшением порога
tps = stable_cumsum (y_true * вес) [threshold_idxs]
если sample_weight не равно None:
fps = stable_cumsum (вес) [threshold_idxs] - tps
еще:
fps = 1 + threshold_idxs - tps
return fps, tps, y_score [threshold_idxs]
重点 从 35 行 开始 , desc_score_indices 得到 了 降序 的 y_score 的 索引 。46 行 np.diff (y_score) 得到 了 y_score 一 差分 n.dp (y_score)) [0] 获得 一 阶 差分 不 为 0 的 索引 列表 , [0] 是 np.где (np.diff (y_score)) 得到 的 是 一个 元 组 , 元 组 的 第 一个 元素 才是 索引 列表。 这里 实际上 就是 对 y_score 做 了 一个 去 重 操作 , 重复 没有 意义 。36 -37 得到 了 降序 的 y_score 和 y_true。 第 47 行将 索引 值 y_true.size - 1 加入 到 了 independent_value_indices 中 , 因为 一 阶 差分 之后 少 了 一个。
50 [threshold_idxs] 首先 对 降序 的 y_true 进行 了 累加 的 操作 , 然后 threshold_idxs 获得 了 累加 结果。 因为 正 是 1 , 负 例 是 0 是 获得 了tps)。 而 54 行 则 获得 了 假 正 例 fp (fps) 。threshold_idxs 的 值 不仅仅是 索引 , 也 代表 了 正负 样例 总和 , 1 + threshold_idxs - tps 就是 假 正 例。
综 上 , roc_auc_score 实现 方式 和 tf.metrics.auc 基本 一致 , 只是 求 小 梯形 面积 时 为 : 小 梯形 个数 不 一样 (阈 值 个数 不同) 和 小 梯形 面积 ( , fp, fn 不同 , 所以 tpr, fpr 不同 进而 导致 小 梯形 面积 不同)。 综合 roc_auc_score 和 tf.metrics.auc 的 实现 , 知道 了 两点 :
- 关于 阈 值 的 个数 , 使用 tf.metrics.auc 时 , 参数 num_thresholds 最好 设置 为 batch size ;
- 阈 值 的 取值 ,好 。tf.metrics.auc 时 等距 划分 , roc_auc_score 是 直接 取 баллы , 仁者 见 仁 见 智 吧。
Очень простое объяснение AUC или Area Under Curve (ROC Curve)
В моделях классификации с машинным обучением одним из распространенных показателей точности модели является AUC или Площадь под кривой. Под кривой подразумевается кривая ROC. ROC означает рабочие характеристики приемника, используемые инженерами-радиолокационными станциями во время Второй мировой войны.
Хотя название кривой ROC осталось, в машинном обучении оно не имеет ничего общего с сигналами радаров или приемниками сигналов. Следовательно, может быть лучше оставить сокращенное название ROC как есть, не пытаясь его расширить. В нашем объяснении AUC мы сведем технические термины к минимуму.
На кривой ROC мы наносим « истинных положительных результатов » на ось Y и « истинных отрицательных » на ось X. При этом давайте объясним и рассмотрим оба этих термина. У нас есть данные с 200 записями.Предположим, что в этих данных 100 записей классифицируются как единицы, а еще 100 записей - как нули. Строится модель прогнозирующей классификации, и делается и проверяется прогноз для общего количества единиц. Предположим, прогноз таков, что количество единиц равно 70, а остальные 30 - нули. Таким образом, истинная положительная ставка (TPR) составляет 70/100 или 0,70.
Теперь предположим, что из 100 записей, классифицированных как нули, предсказание говорит, что 70 из них - это единицы, а 30 - нули. Следовательно, частота ложных срабатываний (FPR) составляет 70% или 0,70. (См. Первый и третий столбцы таблицы ниже) Что происходит, когда FPR (ложноположительный показатель) равен 0.70 соответствует TPR (истинная положительная ставка) 0,70. Согласно прогнозу TPR мы ожидаем 70 единиц (из ста записей, фактически отмеченных как 1), а также согласно FPR, мы ожидаем еще 70 (из общего числа 100 записей, фактически отмеченных как 0), что в общей сложности составляет 140 предсказываются. Из 140 ответов 50% правильные и 50% неправильные. Сейчас тестируется новый рекорд. Он проверяет как 1. Существует 50% -ная вероятность, что это один из истинно-положительных результатов, и еще 50% -ная вероятность, что это один из ложноположительных результатов.
Что, если бы TPR было 40%, а FPR тоже было 40%. Опять же, та же 50% -ная вероятность того, что предсказанный (1) человек принадлежит к одной из двух групп. Таким образом, если FPR нанесен на ось X, а TPR - на ось Y, по всей диагонали у нас будут точки, где TPR и FPR равны. Точки по диагонали представляют ситуацию, которая сродни предсказанию путем подбрасывания несмещенной монеты, то есть модель классификации случайна.
Теперь предположим, что TPR составляет 70%, а FPR - 40%. Прогнозируется один (1) для нового рекорда.Существует вероятность 70 / (70 + 40) = 70/110, что это одна из истинно положительных групп, и 40/110 вероятность того, что она окажется одной из ложноположительной группы. Наша классификационная модель теперь показывает улучшение, чем подбрасывание монеты. Эта точка (FPR, TPR) = (0,4,0,7) находится над диагональю. И, конечно, эта ситуация (модель классификации) относительно все же лучше, чем когда комбинация FPR / TPR составляет (0,4, 0,6). То есть, чем вертикальнее мы размещаем диагональ, тем лучше модель классификации.
Теперь рассмотрим обратное: точка FPR / TPR составляет (0,7,0,4). Прогнозируется один (1). Существует больше шансов (70/110), что он принадлежит к группе ложноположительных результатов, чем к группе истинно положительных результатов (вероятность 40/110). Эта ситуация хуже, чем у модели с шансом 50:50 оказаться по диагонали. Эта точка (0,7,0,4) находится ниже диагонали.
кривых ROC. Зеленая кривая лучше предсказуема, чем красная.
Все модели с точками ниже диагонали имеют худшую производительность, чем модель, которая делает прогнозы случайным образом.
Что, если бы наш начальный набор двоичных классов содержал 100 единиц (единиц) и 50 нулей (нулей) вместо 100 единиц и 100 нулей? Что будет представлять диагональ? В этом случае диагональ по-прежнему будет представлять точки с равными TPR и FPR, но вероятность того, что одна из них будет из группы TPR, будет 2/3, а вероятность того, что она будет из группы FPR, будет 1/3 по всей диагонали; это снова может быть смоделировано случайным процессом, скажем, смещенной монетой.
Как строится кривая ROC : Теперь вы построили модель классификации.Эта модель имеет TPR 0,70 и FPR 0,30. Так что эта модель стоит значительно выше диагонали. Все модели двоичной классификации определяют принадлежность записи к тому или иному классу на основе определенного порогового значения выходных данных модели. Предположим, теперь вы уменьшили этот пороговый уровень. Тогда есть вероятность, что то, что раньше классифицировалось как нули, будет переклассифицировано как единицы. То есть будет увеличение общего количества единиц; общее количество предсказанных нулей не увеличится, хотя может уменьшиться.Это означает, что как TPR, так и FPR увеличатся. См. Следующую таблицу.
Фактический класс Выпуск модели Прогнозируемый класс (отсечка 0,5) Прогнозируемый класс (отсечка 0,45) 1 0,6 1 1 1 0,5 1 1 1 0,5 1 1 1 0.45 0 1 1 0,44 0 0 - – – – 0 0,5 1 1 0 0,5 1 1 0 0,45 0 1 0 0,45 0 1 0 0.4 0 0 - – TPR = 3/5, FPR = 2/5 TPR = 4/5, FPR = 4/5
TPR может увеличиться (или остаться прежним), потому что ранее фактический (1) мог быть ошибочно классифицирован моделью как нулевой (0) из-за высокого порогового значения, но при уменьшении порогового значения он получается правильно классифицируется как 1, увеличивая количество истинных положительных результатов. FPR увеличится, потому что фактический ноль, который правильно классифицировался как ноль, может быть переклассифицирован как 1, что приведет к другому ложному срабатыванию.И FPR, и TPR увеличиваются, и наша точка на плоскости ROC перемещается вправо и вверх. Точно так же увеличение порога уменьшит TPR, а также FPR, и точка переместится вниз-влево (на диаграмме выше точка «a» переместится в точку «b»). Кривая ROC строится путем изменения значения этого порога. Форма кривой ROC зависит от того, насколько разборчивым был результат нашей модели.
Чем больше кривая ROC поднимается вверх и от диагонали, тем лучше модель. Поскольку наша шкала по оси X составляет максимум 1 (FPR может варьироваться от 0 до 100% или 1) и поскольку масштаб по оси Y также является максимальным (TPR может варьироваться от 0 до 100% или 1), общая площадь под прямоугольником ( фактически квадрат) равно 1 * 1 = 1.Чем больше кривая ROC поднимается вверх и от диагонали (и охватывает верхнюю горизонтальную линию, TPR = 1), тем больше площадь будет под ней, и эта область будет ближе к 1. Таким образом, максимально возможная площадь ROC Под кривой может быть 1. Если кривая ROC совпадает с диагональю, площадь под ней равна 0,5 (диагональ делит квадрат / прямоугольник пополам). Мы только что узнали, что ROC-кривая по диагонали - это модель случайной классификации. Площадь под кривой (ROC) известна как AUC. Следовательно, эта область должна быть больше 0.5, чтобы модель была приемлемой; модель с AUC 0,5 или меньше бесполезна. Понятно, что эта область является показателем точности прогноза модели.
 metrics import precision_recall_curve, classification_report
from sklearn.model_selection import train_test_split
df = pd.read_csv('../../data/telecom_churn.csv')
metrics import precision_recall_curve, classification_report
from sklearn.model_selection import train_test_split
df = pd.read_csv('../../data/telecom_churn.csv')
 fit(X_train, y_train)
# Воспользуемся функцией построения матрицы ошибок из документации sklearn
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.
fit(X_train, y_train)
# Воспользуемся функцией построения матрицы ошибок из документации sklearn
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt. tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
font = {'size' : 15}
plt.rc('font', **font)
cnf_matrix = confusion_matrix(y_test, lr.predict(X_test))
plt.figure(figsize=(10, 8))
plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'],
title='Confusion matrix')
plt.savefig("conf_matrix.png")
plt.show()
tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
font = {'size' : 15}
plt.rc('font', **font)
cnf_matrix = confusion_matrix(y_test, lr.predict(X_test))
plt.figure(figsize=(10, 8))
plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'],
title='Confusion matrix')
plt.savefig("conf_matrix.png")
plt.show()
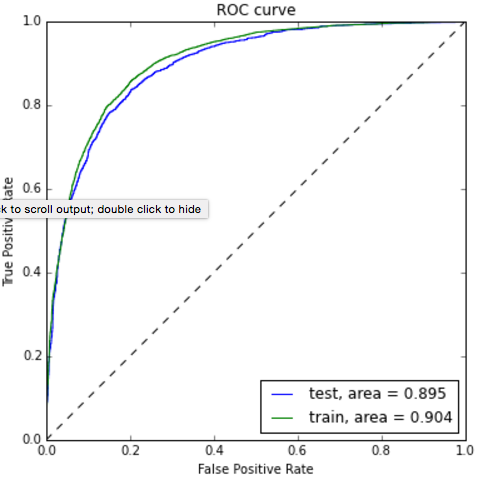 Таким образом,
Таким образом, 693147
print('Logloss при уверенной классификации и верном ответе %f' % logloss_crutch(1, 0.9))
>> Logloss при уверенной классификации и верном ответе 0.105361
print('Logloss при уверенной классификации и НЕверном ответе %f' % logloss_crutch(1, 0.1))
>> Logloss при уверенной классификации и НЕверном ответе 2.302585
693147
print('Logloss при уверенной классификации и верном ответе %f' % logloss_crutch(1, 0.9))
>> Logloss при уверенной классификации и верном ответе 0.105361
print('Logloss при уверенной классификации и НЕверном ответе %f' % logloss_crutch(1, 0.1))
>> Logloss при уверенной классификации и НЕверном ответе 2.302585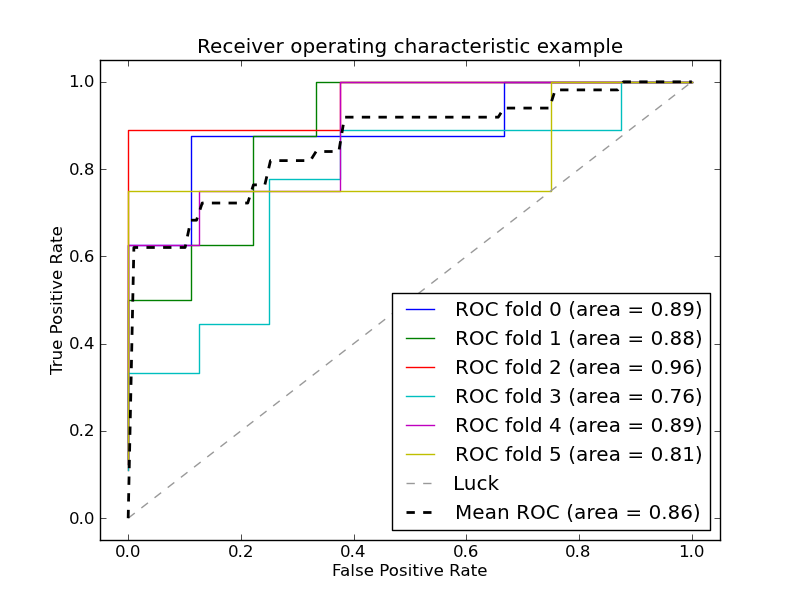 Г. Дьяконова
Г. Дьяконова Age.notnull()].count()
Age.notnull()].count() PassengerId[data.Fare.isnull()]
PassengerId[data.Fare.isnull()]